多少樓才能不擋光

林勇

前幾天勇哥的大學同學在沈陽新買了一套房子，買房本來是件開心的事，妻子卻說樓層（12樓）太低，前樓擋光，抱怨不止.

其實，這種情形在日常生活中屢見不鮮，一提起高樓層我們就稱贊“采光好”，一說到低樓層就抱怨“不見陽光”. 那么問題來了：到底幾樓以上陽光才不會被擋呢？今天我們一起用數學建模的方法嘗試解決生活中大多數人遇到過的這個問題.

問題分析

我們知道，太陽光可以看成是平行光線，樓房都是垂直于地面建造的，我們可以據此畫出如圖1所示的模擬圖，想要知道幾樓以上不擋光，其實就是求當陽光與地面所成的角最小時，乙樓在陽光下的投影落在甲樓的第幾層上.

結合我們學過的三角函數及其應用的知識，可知要解決上述問題需要知道以下幾個變量的數值：

變量1：兩棟樓之間的距離;

變量2：乙樓房的高度;

變量3：樓房的層高;

變量4：陽光與沈陽當地的最小夾角.

經查找資料及咨詢業內人士，勇哥得到相關信息：

（1）每層樓的建筑高度一般為3米左右;

（2）我國相關法規規定，樓高超過100米需要設置避難層，但這會增加樓房的建造成本，因此一般民用住宅樓不超過100米，故我們取樓房高度為100米（約33層）;

（3）樓間距一般為樓高的0.7倍，故我們取樓間距為70米;

（4）冬至這天，太陽直射南回歸線（南緯23°26′，約為23.5°），此時陽光與我國所處的北半球的夾角最小，因此我們需要求出此時陽光與沈陽（約北緯42°）的地面夾角.

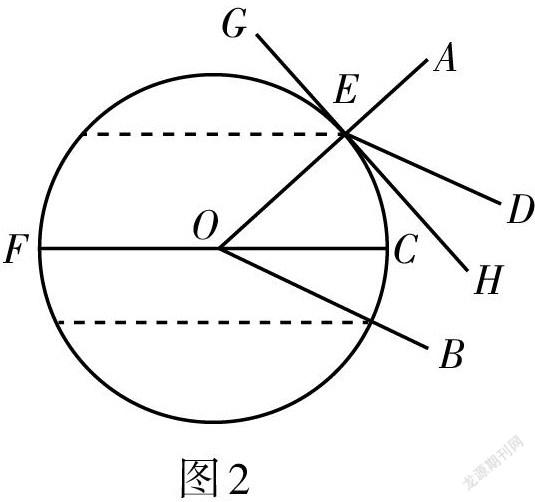
為此我們作出圖2，設地球為標準的圓形，OA為沈陽當地樓房的鉛垂線，BO為冬至時直射在南回歸線的陽光，FC為赤道，DE為照射在沈陽的與BO平行的陽光，GH為沈陽所在位置與地球的切線（即地平線）.

我們首先需要解決如下問題：

已知：如圖2，CF為[⊙]O的直徑，∠BOC = 23.5°，∠AOC = 42°，GH為[⊙]O的切線，切點為E，若DE[?]BO，求∠DEH的大小.

解：∵∠BOC = 23.5°，∠AOC = 42°，

∴∠AOB = ∠BOC + ∠AOC = 65.5°，

∵DE[?]BO，∴∠AED = ∠AOB = 65.5°.

∵GH為[⊙]O的切線，切點為E，

∴∠AEH = 90°，∴∠DEH = ∠AEH - ∠AED = 24.5°.

即陽光與沈陽當地的最小夾角為24.5°.

至此，上面4個變量的數值我們已全部得到，據此可以建立數學模型來解答開篇提出的問題.

建立模型

如圖3，已知AB，CD為兩座高度均為100米的樓房，樓間距BD = 70米，CE為經過樓房CD的頂端射向樓房AB的陽光，若每層樓高3米，當太陽光線與水平地面的夾角為24.5°時，樓房AB幾樓以上才不會被樓房CD的影子遮擋？（tan 24.5° ≈ 0.46）

解：如圖3，作EF⊥CD于F，∵AB⊥BD，CD⊥BD，

∴四邊形BEFD為矩形，∴BE = FD.

在Rt△CEF中，∠CEF = 24.5°，

∴CF = EF·tan∠CEF = 70 × tan 24.5° ≈ 70 × 0.46 = 32.2（米），

∴FD = CD - CF = 100 - 32.2 = 67.8（米），

∴BE = FD = 67.8米.

67.8 ÷ 3 + 1 = 23.6 ≈ 24（樓）.

即當太陽光線與水平地面的夾角為24.5°時，樓房AB的24樓及以上才不會被樓房CD的影子遮擋.

結果分析

由上述計算我們可以得出如下結論：

若沈陽某個樓盤的樓房均為33層（約100米），當其樓間距為70米時，在冬至這一天，24樓以上（包括24樓）才不會被前樓擋光. 因此勇哥同學妻子的擔心是有道理的. 但冬至過后，隨著陽光的直射點離開南回歸線逐漸往北偏移，陽光與水平地面的夾角將變大，24樓以下也會接收到陽光，因此不必過分擔心. 感興趣的同學可以仿照上述方法計算一下夏至這天幾樓會被擋光.

建模心得

由于條件所限，上述分析過程中我們所選取的數值均為理想狀況.現實生活中，樓的層高、樓房的總高度、樓間距、樓房所在緯度等均會有所變化，同學們可以在實地測量后再進行計算.

數學建模是一種科學的思考方法，熟練掌握這種方法可以準確刻畫并解決實際問題. 同學們要掌握數學建模方法，多觀察、多思考，學會用數學眼光來思考問題.