一種基于Dijkstra算法的動態進路規劃方法

金 云，周 苗，黃仁歡，虞乾儷

（通號萬全信號設備有限公司，杭州 310000）

工業鐵路通常由多個不同功能的站場組成，設置公司級調度和站級調度的兩級調度模式來對公司內專用鐵路進行調度指揮。分散的調度權將一個完整的生產作業過程分割開來，影響企業的生產作業效率。隨著自動化、信息化技術的進步，繁瑣的企業內部鐵路運輸可以通過技術手段整合。采用集中調度模式，只在公司級設置一級調度，同時提供調度系統的自動化、智能化，減少調度人員，提高生產效率。

進路搜索是工業鐵路智能調度管理系統的基本功能，其運行效率以及所得目標進路直接關系到企業運輸計劃的高效性和準確性。本文通過對站場數據的組織，將站場圖抽象為無向帶權連通圖，建立靜態網絡拓撲圖，在此基礎上通過道岔、區段的實時狀態，動態調整無向網絡拓撲圖中各個邊的權重，基于圖論中的最短路徑算法模型，完成起始無岔區段到目標無岔區段的路徑規劃，再與系統中的基本進路進行進路中最多元素的模糊匹配，自動生成進路列表，以供系統做自動進路的觸發。

1 最短路徑算法介紹

對于帶權圖G=（V,E），從圖中任意一點vi到圖中任意一點vj的邊的權值定義為路徑所包含的所有元素權值的總和，而不是邊所包含的所有元素個數的總和。最短路徑求解問題可以分成兩個不同的子問題，即單源最短路徑問題和所有頂點對之間的最短路徑問題。前者是找出某一頂點出發到圖中所有其他頂點的最短路徑，主要的算法有迪杰斯特拉（Dijkstra）算法、貝爾曼-福特（Bellman-ford）算法等；后者是求解圖中的每一對頂點之間的最短路徑，主要算法有弗洛伊德（Floyd）算法。現有的使用場景為計算指定的兩個點之間的最短路徑，故首先選擇單源最短路徑問題所對應的算法。

Dijkstra算法是貪心算法的一種，按照路徑長度遞增的次序產生最短路徑的算法，無法處理帶有負權值的圖。但是該算法的穩定性很強。基礎算法時間復雜度為O(V2)，對于稀疏圖(邊的數量遠小于頂點數的平方)，該算法的時間復雜度可以提高至O(ELgV)。Bellman-ford算法能夠處理帶有負權值的圖，但是該算法的穩定性不如Dijkstra算法，基礎算法的時間復雜度為O(V×E)。其中E為圖中的邊數，V為圖中頂點個數。

本文所涉及的靜態網絡拓撲圖中邊的權值全都是非負值，而且該圖是一張稀疏圖。故選擇Dijkstra算法作為最短路徑的求解比較適合本應用場景。

2 靜態拓撲圖生成

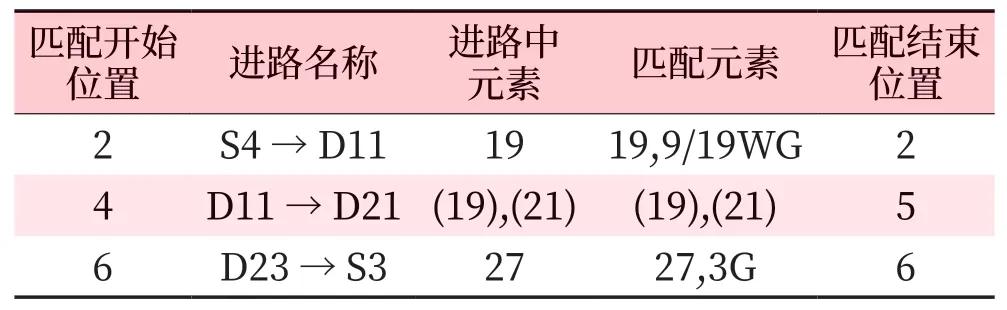
系統內的道岔全都定義為單動道岔，如果是雙動道岔，則通過內部邏輯的聚合，按照一個道岔數據對外提供，但是在系統內都按照獨立運算。根據道岔和無岔區段的鏈接關系數據，自動創建一張無向帶權的網絡拓撲圖。生成的靜態網絡拓撲圖則由點的集合V(G)={vi}和邊的集合E(G)={eij(i

點集V(G)中的點ei代表站場圖中的第i個無岔區段。邊集E(G)中的邊eij(i

3 最短路徑生成算法

對于圖G={V(G),E(G)}，假設需要求無岔區段s到無岔區段e的最短路徑。

1）權值初始化，根據站場中的道岔、區段、信號機的實時狀態，動態修改該設備所在邊的權值。例如道岔封鎖，則設置包含該道岔的邊的權值為∞，代表該邊不可達，道岔單鎖在指定位置，則設置包含該道岔相反位置的邊為不可達邊。區段占壓、封鎖等，則設置該區段所在邊的權值為∞，代表該邊不可達。信號機封鎖、斷絲等，則設置該信號機的防護區段所在邊的權值為∞，代表該邊不可達。

2）設頂點集Vc(G)=?和邊集Ec(G)=?，從圖G中的頂點集V(G)中取出開始區段s所對應的點vs,把vs放入頂點集Vc(G)中。此時Vc(G)={vs},V(G)=V(G)-Vc(G)。

3）從圖G中的邊集E(G)中取出一個臨時邊集Et(G)={eij,…|(vi∈Vc(G)&&vj∈V(G)) ||(vi∈V(G)&&vj∈Vc(G)) }，

即對于Et(G)集合中的任意邊eij，其中eij的兩個端點分別屬于兩個不同的頂點集合V(G)和Vc(G)。

如果Et(G)為空集或者Et(G)中所有邊的權值都是∞，則無法找到最短路徑，算法退出。

如果Et(G)中存在可達邊，設eij∈Et(G)為集合中權值最小的邊，則把邊eij添加到集合Ec(G)中。

4）在vj中標記父節點為vi，并且把點vj添加到集合Vc(G)中。

如果vj就是無岔區段e所對應的點，則找到該最短路徑。算法退出。

如果vj不是無岔區段e所對應的點，則把Et(G)中兩個頂點都在Vc(G)中的邊從該集合中刪除Et(G)= {eij,…|(vi∈V(G)&&vj∈V(G)} 。把Et(G)中的剩余邊全都放回集合E(G)中。

5）重復從步驟3）開始執行，直到頂點集合V(G)中不再包含任何頂點為止。

4 進路轉換

按照結束頂點中包含的父節點信息以及邊中道岔的先后順序(邊的雙下標和點的順序一致，則邊中的道岔按照正序輸出。邊的雙下標和點的順序相反，則邊中的道岔按照逆序輸出)，把Dijkstra算法生成的路徑轉化為站場中的各個基本元素。由于站場中的基本進路有些只包含一個道岔區段，可能會出現匹配到的進路方向和規劃路徑的方向相反，故針對進路中只有一個道岔區段的，則自動把該道岔區段后面的元素臨時添加到該基本進路中。對于相同始端的進路，在進路都覆蓋最短路徑元素的前提下，保留進路中包含元素多的進路作為臨時候補進路，同時記錄該進路匹配開始的元素在最短路徑元素中的位置。當所有進路匹配完畢后，按照記錄的起始位置進路排序，按照進路的開始位置和結束位置，刪除中間有交叉的進路。當最短路徑中的道岔元素匹配完畢，則最短路徑轉化為進路成功。

例如按照如圖1所示，假設列車需要由4G運行到3G。

1）按照Dijkstra算法計算出最短路徑:4G→9/19WG→3G。

2）由路徑轉化為基礎元素為: 4G→19→9/19WG → (19) → (21) → 27 → 3G。

3）基本進路匹配的臨時候選進路如表1所示(其中S4→D11，D23→S3只包含一個道岔區段，故匹配時增加一個后續連接區段)。

表1 進路匹配Tab.1 Route matching

4）臨時候補進路的匹配開始位置和匹配結束位置沒有出現交錯的情況，全都轉化為候補進路。如果臨時候補進路的匹配位置出現交錯，則把匹配開始位置大的進路從臨時候補進路中剔除掉。

5）把路徑基礎元素列表中的元素按照候補進路中的道岔區段元素進行比較，去除掉相同元素。進路基礎元素列表變為：4G、9/19WG，3G。

6）除去道岔區段后的路徑基礎元素列表中如果不包含道岔區段，則最短路徑轉化為基本進路成功。如果包含道岔區段，那么最短路徑轉化為聯鎖進路失敗。

5 結束語

工業鐵路運輸調度的主要任務就是列車把貨物從一個股道拉到另一個股道，并且摻雜著一些裝車、卸車等標準作業內容。而從一個股道到達另一個股道就需要調度員根據自己對站場的認識，一步一步的人工排列聯鎖進路來指導火車運行。基于本算法的進路動態規劃方法，系統只需要輸入目標股道信息，即可自動計算、選擇出最優的聯鎖進路組合，根據列車的實時位置，自動執行計劃進路，實現運動過程的自動化。而且針對聯鎖站場的實時變化，自動進路也不一定百分之百辦理。當出現進路自動觸發失敗的情況，系統可以通過列車當前位置和目的地信息，自動重新規劃，更新進路表，保證列車以最優的路線抵達目標股道進行標準作業。Dijkstra算法的實現，大大減少信號調度人員的工作量，保證調度工作的準確完成，中間的全自動過程為后期實現全面無人駕駛打下了堅實的基礎。