ON REFINED YOUNG’S REVERSE INEQUALITIES FOR POSITIVE LINEAR OPERATORS
CAO Hai-song
(School of Mathematics and Statistics,North China University of Water Resources and Electric Power,Zhengzhou 450045,China)
Abstract:In this paper,the inverse inequalities of Young for positive linear operators are studied.By using the properties of operators’monotone function and convex function,we obtained some improved scalar versions and corresponding operator versions of Young’s inverse inequality with Kantorovich constant,which generalize the conclusions in the literature.
Keywords: Young’s reverse inequality;positive linear operators;Kantorovich constant
1 Introduction
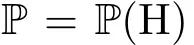
The classical Young inequality says that if a,b≥0 and 0≤v≤1,then

with equality if and only if a=b.
This inequality has been studied,generalized and re fined in different directions,see[1-2].It is worth to mention that in[3],J.L.Wu and J.G.Zhao presented re fined and reversed versions of the scalar Young type inequality which can be stated as follows:
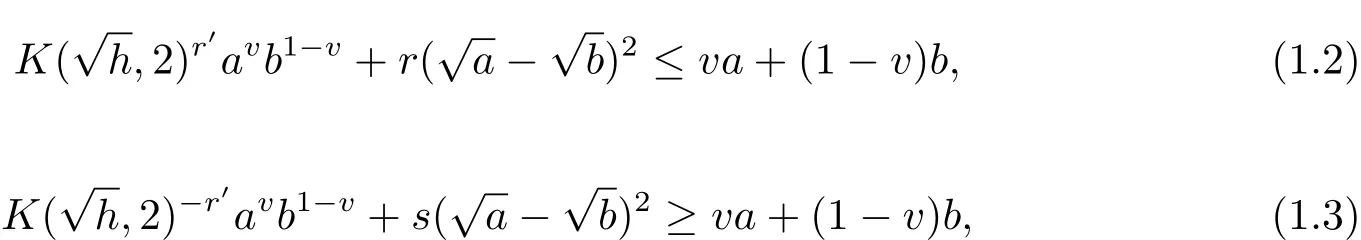
In[4],a more re fined version was presented which can be stated as follows:

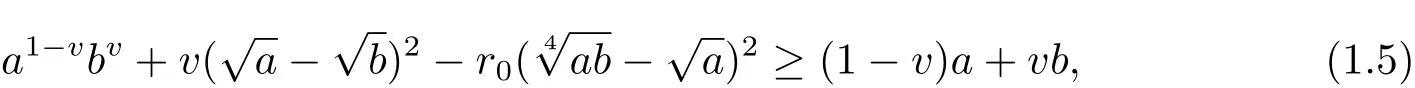
where a,b>0,v∈(0,1),r=min{v,1-v}and r0=min{2r,1-2r}.
Let A,B∈B(H)be two positive operators,v∈[0,1].
v-weighted arithmetic mean of A and B,denoted by A?vB,is defined as
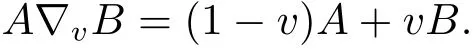
If A is invertible,v-geometric mean of of A and B,denoted by A#vB,is defined as
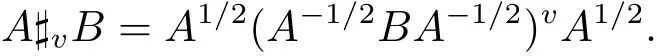
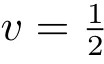

In[6],S.Furuichi gave a refinement version:
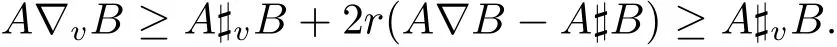
In[4],J.Zhao and J.Wu presented other improved inequalities:
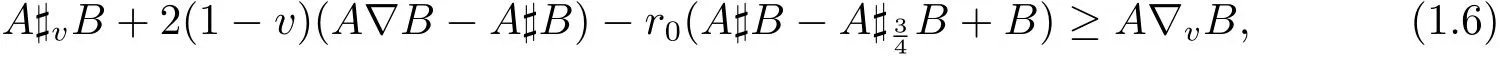
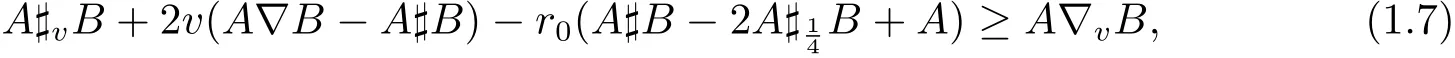
where A,B∈B(H)are two positive invertible operators,v∈(0,1),r=min{v,1-v}and r0=min{2r,1-2r}.
Since then,many researchers have tried to give new refinements and generalizations of these inequalities and have obtained a series of improvements,one can refer to the references of[7-9].
In this paper,some Young’s reverse inequalities with Kantorovich constant for scalars were presented which are improvements of(1.3)~(1.5).Then on the base of them,the corresponding variations of recent refinements for positive linear operators were obtained which are refinements of(1.6)and(1.7).
2 Refinements of the Young’s Reverse Inequality for Scalars
In this section,some improved Young’s reverse inequalities with Kantorovich constant for scalars were presented.
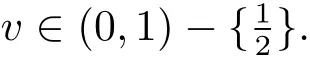

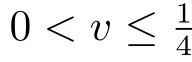

This completes the proof.
Remark 2.1Obviously R ≥ 0 and K(·,h)≥ 1,so the inequalities(2.1) ~ (2.4)are the improvements of the scalar Young type inequalities(1.3)~(1.4).
3 Operator Inequalities for the Improved Young Inequalities
Based on the improvements of the scalar Young type inequalities(2.1)~(2.4),we present corresponding operator inequalities for the improved Young inequalities.
Lemma 3.1Let X∈B(H)be self-adjoint and let f and g be continuous real functions such that f(t)≥g(t)for all t∈Sp(X)(the spectrum of X).Then f(X)≥g(X).
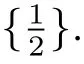

ProofThe proof of inequalities(3.2)~(3.4)are similar to that of inequality(3.1).Thus,we only need to prove the inequality(3.1).
for any b>0,which for X=A-1/2BA-1/2and thus for Sp(X)?(0,+∞),then
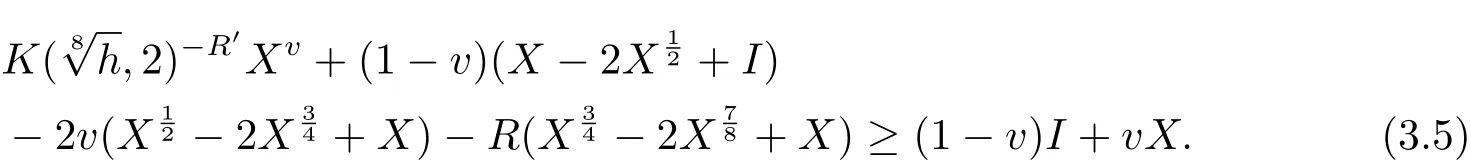
Multiplying both sides of(3.5)by A1/2,we get
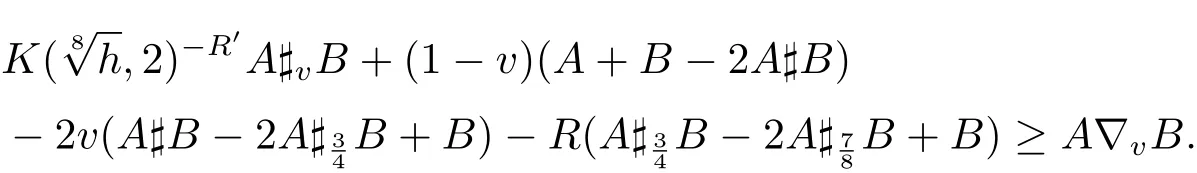
This is equal to
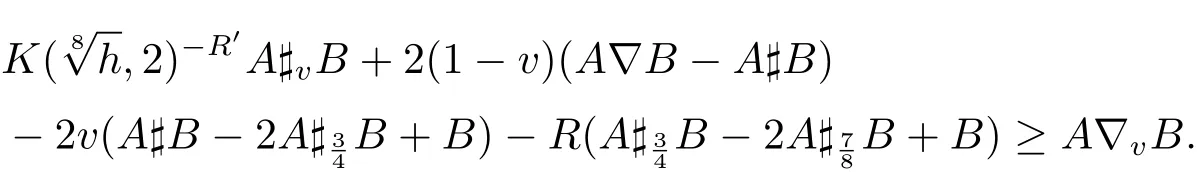
This completes the proof.
- 數學雜志的其它文章
- 牽制控制含噪聲的多延遲超網絡的結構識別
- 一類帶粘性項的拋物方程解的存在性和爆破性
- NUMERICAL DYNAMICS OF NONSTANDARD FINITE DIFFERENCE METHOD FOR MACKEY-GLASS SYSTEM
- RESEARCH ANNOUNCEMENTS ON“UPPER BOUND ESTIMATES OF EIGENVALUES FOR HRMANDER OPERATORS ON NON-EQUIREGULAR SUB-RIEMANNIAN MANIFOLDS”
- ON SPLIT REGULAR BIHOM-LIE COLOR ALGEBRAS
- THE SPREADING SPEED FOR A NONLOCAL DIFFUSIVE PREDATOR-PREY MODEL WITH ONE PREDATOR AND TWO PREYS

