海上搜救力量配置問題研究*

任東彥

（海軍軍醫大學海軍衛勤訓練基地 上海 200433）

1 引言

海上搜救是一個世界性難題，特別是海上作戰中對落水人員的搜救工作難度更大。這是由于海上環境惡劣，且海域廣闊，傷員分布廣泛，人員落水后，若長時間得不到救治，受低溫、海洋有害生物侵襲、淡水和食物缺乏等影響，極易死亡，因此，加強戰時海上落水人員搜救工作的相關研究具有十分重要的意義。海上落水人員包括由于戰損、碰撞、故障、觸礁、火災、傾覆、進水、失控等各種原因而導致的處于海面險境的艦船落水人員、戰斗機落水飛行員等人員，對落水人員搜救的關鍵是爭取時間[1～2]。這其中，搜救力量能否科學配置并迅速準確到達搜救海域是搜救工作成敗的關鍵，本文針對海上搜救力量配置問題進行研究，在定性分析的基礎上建立海上搜救力量配置解析模型，為海上搜救力量配置提供理論參考，有助于提高海上搜救效率。

2 搜救作業區的優化配置

達到高效率，是海上搜救工作所要達到的基本目標之一。為了以最快速度搜索到落水人員，海上搜救力量配置的前提是要合理劃分搜救作業區。

2.1 搜救作業區的選擇

在搜救過程中，為了將搜救區域限制在盡可能小的范圍內，需要確定基本搜救區。基本搜救區就是根據已知落水人員信息或已發現落水人員的位置結合海區海流流向和風向初步確定的搜救區。理論上，基本搜救區的形狀可以有很多種，但在實際應用中，為便于搜救行動，一般情況下，多將搜救區確定為矩形。確定基本搜救區的原則是搜救區既包含所有搜救目標又滿足面積最小。

按照這一原則，基本搜救區是包含某一組中所有搜救目標且面積最小的外接矩形。為滿足這一要求，就要針對已發現搜救目標計算多個面積。一般而言，由于這里所確定的搜救區僅僅是概略的，因此只要大致方向差不多就可以滿足要求，例如選取0，60°，90°三個方向的外接矩形進行計算和比較，從中選出面積最小的。但現代搜救艦船多攜帶有直升機，對直升機搜救而言，風向對直升機飛行穩定性、航跡保持和懸停點間的過渡影響很大。因此，在對基本搜救區進行選擇時，一般按照風向選擇外接矩形[3]。

2.2 搜救作業區的合理劃分

當搜救海域面積較大時，為便于搜救行動，可將搜救作業區劃分為若干地段，對每個地段編號并劃定作業區，由搜救力量按編號逐段搜索。劃分搜救地段時按下列要求進行。

1）盡量將某一類搜救目標劃分到一個作業區內；

2）保持搜救帶為直向配置；

3）便于轉向機動。

2.3 搜救方向的確定

搜救方向是指艦船或直升機在劃分好的搜救作業區內實施搜索時的起始方向。確定搜救方向時，應根據下列情況綜合分析比較，抓住主要矛盾：

1）盡量與搜救作業區邊長方向一致；

2）盡量與風向平行，以便直升機搜索發現目標時迎風懸停；

3）便于艦船和直升機轉向機動；

4）盡量減少轉向次數。

2.4 搜救起點和順序的確定

搜救起點是指艦船或直升機在劃分好的搜救作業區內實施搜索時的起始位置。確定搜救起點，應考慮下列因素：

1）一般應從搜救作業區邊緣開始，逐帶順序搜索，也可從航道或地域中心線開始，逐帶向兩側擴大；

2）搜救帶按順序以羅馬字母標注，確定了搜救起點，也即確定了搜救的順序。

3 海上搜救方法

海上搜救一般結合具體任務由艦船或直升機完成。實施海上搜救，搜索目標是前提，只有及時準確地搜索到目標才能實現以最大的效率救治目標。在搜救過程中，多數情況下，應根據搜救任務的需要，在搜救作業區的優化配置的基礎上，進一步確定搜救方法。搜救方法就是指艦船或直升機相鄰搜索帶之間的配置方法[4～5]。搜救方法為相鄰搜索航路的搜索寬度之間有一定的重疊，重疊寬度一般為二倍航跡均方誤差（2δ），見圖1。搜索帶的實際寬度，可按下式求得：BS=B-2δ。

圖1 搜索航線

4 海上搜索樣式

搜索樣式是指在確定搜救作業區的位置、大小、形狀后，對搭載搜索設備的搜救力量在搜救作業區的路線規劃和運用方式。選擇搜索樣式的主要依據有落水人員位置坐標預測的準確性、搜救作業區的大小和形狀、搜救力量的定位精度。適用于對海搜索的方法主要有扇形搜索、擴展方形搜索、橫移線搜索和平行線搜索。分析四種搜索方式，對比如表1所示。

表1 搜索方式對比

從表1中可以看出，扇形搜索樣式和方形擴展搜索適用于定基點小范圍的小散布區域落水人員的搜索，但不適合多個搜救力量協同搜索；平行線搜索適合于不定基點的大范圍區域搜索，能夠運用多種搜救力量協同搜索；橫移線搜索適合不定基點的長且窄的大范圍區域搜索，適合直升機或艦機協同搜索。

5 海上搜救力量配置算法

戰時，為了提高海上落水人員救治效率，要求搜救兵力在規定的時間內必須完成規定海域的搜索，因此，提高海上落水人員救治效率的前提是要達到較高的搜索效率。在搜救作業區滿足戰術要求并合理劃分的基礎上，應科學配置搜救兵力并迅速完成各項搜索任務。

假設在某海域內（面積為S）內實施搜索，預先只了解該海域存在落水人員，并不了解有關落水人員的具體位置。可假設目標在該區域內均勻分布，在搜索過程中，將搜索海域劃分為若干小段（設其個數為n），每一小段采用平行線樣式對搜索海區進行覆蓋。

搜索區域是長為L1、寬為L2的矩形，搜索寬度為l，搜救力量速度為v，相鄰搜索帶之間的重復區域為二倍航跡均方誤差（2δ），每次180°轉向所需的時間為Δt。

搜索區域面積即為L1·L2，如圖2所示。則目標出現在某一小段之內的概率為

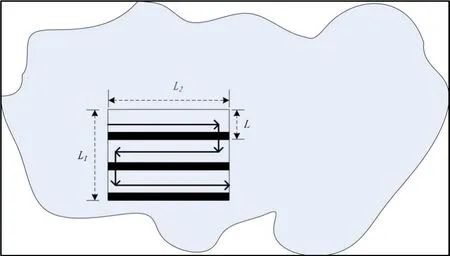
圖2 平行線搜索覆蓋區域

如圖2根據幾何關系可得，對該矩形搜索區域進行一次全覆蓋搜索，搜救力量所需要往返次數為

其中n1為進位取整的正整數。

則搜索力量搜索過的航路距離長為

所需的時間為

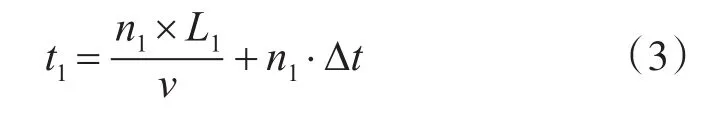
由此，在計算海上搜救力量配置數量時，可結合具體的搜救任務，根據要求的搜救時間t1反向計算出航線距離長為d1和搜索力量所需要往返次數為n1，進而可計算出海上搜救力量配置數量。

6 示例

假設在某次海上作戰中，紅方1艘護衛艦被敵方一枚反艦導彈擊中，導致15名人員落水（位遠海某島西南15海里附近海域），見圖3。編隊指揮部接到求救信號后即組織搜救艦船對落水人員的搜救。

1）搜救作業區的優化選擇

根據受損艦船位置或已知落水人員信息或已發現落水人員的位置并考慮風向、海流流向等海區地理水文氣象資料，初步將70°方向的外接矩形確定為搜救作業區，編號為S，搜救作業區長L為10km，寬W為6km，如圖3所示。

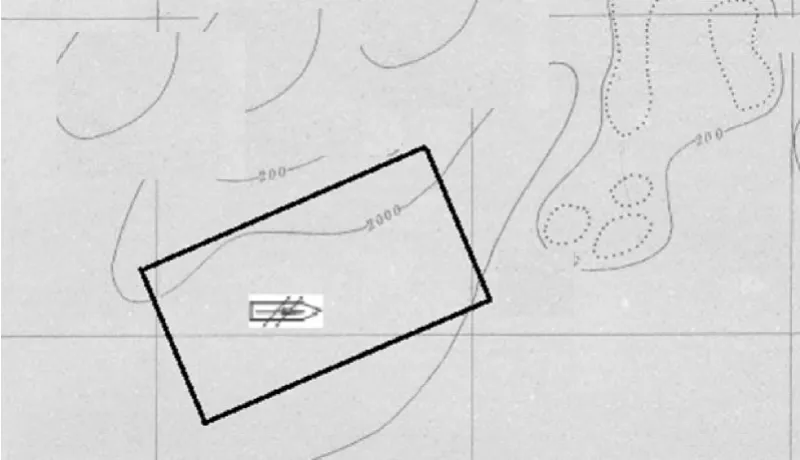
圖3 受損艦船搜救作業區

2）海上搜救力量配置數量

在S海域內實施搜救，因為預先只了解該海域存在落水人員，并不了解有關落水人員的所有具體位置，可假設目標在該區域內均勻分布。根據對海上落水人員的搜索樣式分析，平行線樣式完成全覆蓋的時間更少，所需航路距離更短，具有較高的搜索效率。可將搜索海域劃分為若干小段（設其個數為 n），編號分別為 S1，S2，…，Sn，每一小段采用平行線樣式對搜索海區進行覆蓋，n即為搜救力量配置數量。

考慮傷員的時效救治，上級要求搜救兵力在1h內必須完成全部海域的搜索；搜索海域S1，S2，…，Sn是長L1為10KM，寬為L2待定的矩形區域，搜索寬度l綜合考慮海區氣象條件設定為1000m，搜救艦船速度v設定為15kn，相鄰搜索帶之間的重復區域（二倍航跡均方誤差2δ）設定為50m，艦船每次180°轉向所需的時間Δt設定為3min。

根據幾何關系可得，對該矩形搜索區域進行一次全覆蓋搜索，搜救力量所需要往返次數為

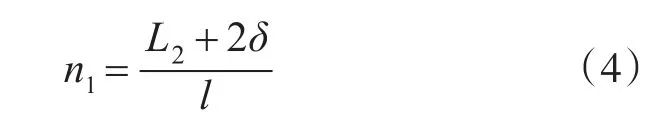
其中n1為進位取整的正整數。

所需的搜救時間為

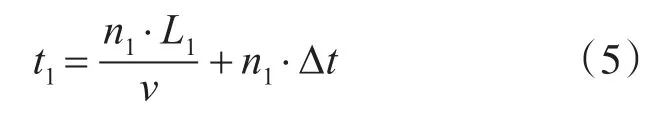
且滿足約束條件：t1≤1。

由式（4）、（5）可計算出搜救海域寬L2，則：搜救力量配置數量為

其中n為進位取整的正整數。

將數據代入式（4）、（5）、（6）計算可得：

由于n為進位取整的正整數，則：n=3。

根據計算結果，完成上級要求在1h內對全部海域的搜索，指揮部結合現有搜救力量，需至少配置3艘搜救艦船分別完成對搜索海域S1，S2，S3的搜索，見圖4。

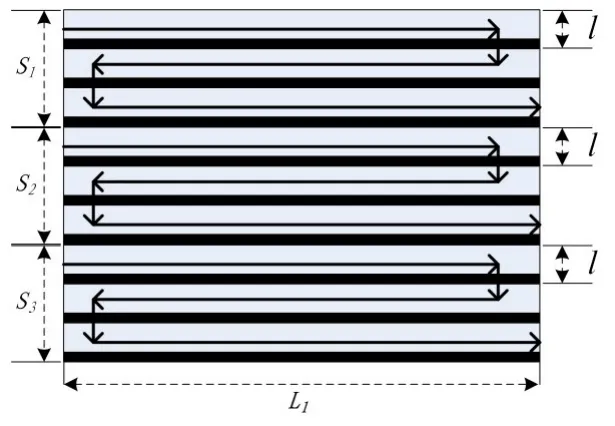
圖4 平行線搜索覆蓋區域

7 結語

由于海上環境的復雜性，各國海軍都十分重視海上搜救的研究。本文首先對搜救作業區的優化選擇方法進行了研究，明確了艦船或直升機在劃分好的搜救作業區內實施搜索時的起始方向、搜救起點和順序，在對海上搜索方法和搜索樣式分析的基礎上，重點對海上搜救力量配置數量計算方法進行研究，在定性分析的基礎上建立海上搜救力量配置解析模型，以期進一步豐富海上搜救理論，為海上搜救力量配置提供理論依據，輔助海上搜救指揮決策。