一種抑制脈沖噪聲的LFM信號參數估計方法

張榆紅，張益鑫，張 超，包軍民

(西安工程大學 電子信息學院，陜西 西安 710048)

線性調頻(Liner Frequency Modulation，LFM)信號廣泛應用于雷達、通信、聲納和生物醫學等領域，是一種低截獲概率雷達非平穩信號。同時，線性調頻信號還可以表征多種頻率時變特性復雜的其他信號，其檢測和參數估計具有重大的意義[1]。迄今為止，已有很多國內外學者提出了一些有效的檢測與估計方法。其中，極大似然估計(Maximum Likelihood Estimation，MLE)方法占有重要地位，其估計值精度高，可以逼近克拉美羅(Cramer-Rao Lower Bound，CRLB)[2]界，但由于要優化非線性代價函數，其運算復雜度也高。以Wigner-Ville分布(Wigner-Ville Distribution，WVD)[3]和短時傅里葉變換(Short Time Fourier Transform，STFT)[4]為代表的常規線性時頻分析方法中，短時傅里葉變換是最早提出的時頻分析方法，其主要原理是通過加窗來處理觀測信號，對窗內的信號進行傅里葉變換，該方法雖然能夠避免交叉項的干擾，但是在低信噪比下性能嚴重下降；WVD的主要原理是對信號相關函數進行某種線性變換，該類方法具有理想的分辨率和高能量聚集性，但是在分析多分量線性調頻信號時會出現嚴重的交叉項。聯合WVD和Hough變換得到的WHT(Wigner-ville Hough Transform)[5-6]能夠降低交叉項的影響，但是不能完全消除其影響，且計算量巨大，不利于工程上的應用。小波變換(Wavelet Transform，WT)[7]屬于多分辨率分析方法，與短時傅里葉變換不同的是，它可以隨著信號的變化自動調節窗的寬度，但是由于小波基的選取太難，并且不同的小波基會有不同的分析結果，所以小波變換的實時性能比較差。分數階傅里葉變換(Fractional Fourier Transform，FrFT)[8]是在傅里葉變換的基礎上提出的新理論，其實質是對線性調頻信號進行不同階數的分數階傅里葉變換，然后根據信號能量聚集性的差異，利用峰值搜索來實現對目標信號的檢測和參數估計，但是分數階傅里葉變換需要進行二維搜索，計算量太大。

以上方法都是在高斯噪聲背景下進行的。而在實際應用中，水聲噪聲、大氣噪聲、多用戶干擾和雷達雜波等廣泛的噪聲類型都屬于非高斯噪聲，這些噪聲類型都表現出明顯的脈沖特性，可以用脈沖噪聲來描述[9]。但在強脈沖噪聲背景下，上述檢測方法的性能嚴重下降。Alpha穩定分布噪聲模型因具有顯著的脈沖特性和厚重拖尾，可以很好地表征這類噪聲。文獻[10]把分數低階協方差應用到了WHT和LV’s Distribution (LVD)，提出了FLOWHT(Fractional Lower Oder Wigner-ville Hough Transform)和FLOLVD(Fractional Lower Oder LV’s Distribution)方法。FLOLVD抑制脈沖噪聲的能力優于FLOWHT，可以實現脈沖噪聲環境中線性調頻信號的參數估計，但是該方法依賴于噪聲的先驗知識，并且當分數低階矩的數值不合適時，算法性能會嚴重下降。在文獻[11]中提出了一種非線性變換函數A-NTA，并將其應用到LVD，能夠很好地抑制強脈沖噪聲，并且不依賴于噪聲的先驗知識，但是該方法僅是針對抑制強脈沖噪聲，在脈沖噪聲較弱或者當處于極低信噪比時，其檢測性能嚴重下降，限制性比較大。在文獻[12]中，使用Sigmoid函數處理的信號全部假設為實信號，在遇到復信號的時候，該方法就可能失效了。

針對以上問題，綜合LVD[11]的原理及Sigmoid[13-14]的性質，筆者提出了一種新的方法——Sigmoid-LVD。首先用非線性函數Sigmoid處理原始信號，在處理信號后再除以信號的共軛；然后根據LVD的定義對Sigmoid變換的對稱瞬時自相關函數沿時間軸t和時延軸τ進行二維傅里葉變換。通過仿真實驗證明，該算法能夠有效地抑制脈沖噪聲，并且不依賴于噪聲的先驗知識，不僅能夠準確地檢測和估計線性調頻信號的參數，而且能夠實現對復信號的檢測和參數估計，更利于在信號處理中的應用。

1 Alpha穩定分布噪聲模型

常規的線性調頻信號檢測方法多基于高斯假設，但在實際應用中，水聲噪聲、大氣噪聲、多用戶干擾和雷達雜波等通常表現為非高斯特性，而Alpha穩定分布模型可以很好地模擬這種類型的脈沖噪聲。用特征函數表達式描述這種模型[15]：

φ(t)=exp{jat-γ|t|α[1+jβsgn(t)ω(t，α)]} ，

(1)

其中，

(2)

(3)

sgn(t)表示符號函數。

Alpha穩定分布可由特征指數α、分散系數γ、對稱參數β和位置參數a確定。各參數所代表的含義如下：α為特征指數，用來度量噪聲脈沖特性的強弱。α越小，表示分布的拖尾越厚。隨著α值的增大，則越趨向于高斯過程。特別地，當α=2時，該分布為高斯分布；當α=1時，該分布為柯西分布。γ為分散系數，表征樣本的分散程度，類似于高斯分布中的方差。β為對稱參數，用于描述分布的斜度。當β=0時，一般稱此分布為對稱Alpha穩定分布，記為SαS。在SαS分布中，當1<α<2時，a表示其均值；當β=0，a=0時，該分布為標準SαS分布。

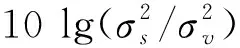
2 LVD原理

LVD無須搜索，也無須引入階數和旋轉角度等非物理屬性。它在時間延遲瞬時自相關函數中引入了一個時延變量，并且重新對時間軸進行變標以消除線性頻率偏移效應[9]。為了明確解釋LVD的原理，將一個連續的無限時間多組分線性調頻信號定義如下：

(4)

其中，Ai是第i個分量的幅值，fi為第i個分量的中心頻率，ki表示第i個分量的調頻斜率。

LVD算法能夠將線性調頻信號的物理特征在中心頻率-調頻斜率域直接顯示出來。其對稱參數瞬時自相關函數定義如下：

(5)

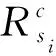
為了消除類似式(5)中的耦合，用Keystone變換[15]的思想來達到去耦合的目的。給定一個與(t，τ)相關的相位函數G，尺度變換函數如下：

(6)

其中，h是尺度因子。當h=1時，其性能達到最優。tn是尺度變換時間，tn=(τ+a)ht。將尺度變換函數應用到式(5)，得

(7)

式(7)表明，對于每個自項，由于引入了新的時間tn，時間變量t和時延變量τ之間的耦合消除了。對式(7)進行二維傅里葉變換，得到LVD的定義：

(8)

其中，F{·}是傅里葉變換算子。LVD與分數階傅里葉變換(FrFT)等方法相比，不需要任何的搜索步驟，降低了計算難度和時間。

LVD中每個自項均能建模為理想的點擴展函數：

(9)

LVD通過增強自項可以對交叉項達到抑制且不會造成任何分辨率損失，表現為近似線性的性質，因此可得

(10)

下面分別給出無噪聲、高斯噪聲、Alpha噪聲下單分量LVD的檢測結果。信號參數為：幅度A=1，中心頻率f0=30 Hz，調頻斜率k=50 Hz/s，有效時間長度T=1 s，采樣頻率fs=512 Hz。從圖1中可以看出，在無噪聲的情況下LVD可以準確地檢測和估計信號參數；在高斯噪聲中，雖然受到噪聲干擾，但是仍可以準確檢測；在Alpha噪聲下，由于受脈沖噪聲的影響，算法失效。

(a)無噪聲

3 基于Sigmoid-LVD的線性調頻信號參數估計方法

3.1 Sigmoid-LVD算法原理

在Alpha穩定分布的噪聲環境下，傳統的線性調頻信號檢測方法的性能嚴重下降。在強脈沖和低信噪比下，信號湮沒在噪聲中，傳統的方法無法有效地完成檢測。為了解決該問題，筆者提出了一種新的方法——Sigmoid-LVD，不僅能夠有效地抑制脈沖噪聲，并且不依賴于噪聲的先驗知識，而且可以更加精確地檢測和估計線性調頻信號的參數。

在實際應用中，非線性函數可以用來抑制Alpha低階穩定噪聲，而理想的非線性變換函數應當具備以下兩點[16-17]：(1)能夠消除Alpha穩定分布噪聲的影響；(2)不會對信號造成嚴重的失真。文獻[16]采用了目前在人工神經網絡中廣泛應用的非線性函數Sigmoid。它的定義如下：

(11)

Sigmoid具有以下3個性質[16]：

(1) 如果s(t)是一個SαS過程，其中a=0，β=0，那么Sigmoid[s(t)]是概率密度函數中均值為零的對稱分布。

(2) 如果s(t)是一個SαS過程，其中a=0，γ>0，則有‖Sigmoid[s(t)]‖α>0，而且當1<α≤2時，Sigmoid[s(t)]的平均值為零。

(3) 如果s(t)是一個SαS過程，其中a=0，1<α≤2，則Sigmoid[s(t)]是具有零均值的有限二階矩(稱為二階矩過程)。

在以上3條性質的基礎上，可以推出Sigmoid的性質4：假設S(t)=Sigmoid[s(t)]，則S(t)具有與s(t)相同的調制特性[17]。根據傅里葉變換的頻移特性，證明過程如下：

證明 設s2(t)=s(ω0t)，可以得到S2(t)=Sigmoid[s2(t)]=Sigmoid[s(ω0t)]=S(ω0t)。

(12)

由上面的公式可得，s2(t)和s(t)之間的頻移與S2(t)和S(t)之間的頻移是相同的，并且隨著參數ω0的變化，頻移可以是任意的。因此可得，S(t)與s(t)有相同的調制特性，即線性調頻信號經過Sigmoid函數處理后，其中心頻率和調頻斜率不發生改變。

把Sigmoid函數與LVD的定義結合，其對稱瞬時自相關函數為

(13)

為了消除時間變量t和時延變量τ之間的耦合，把前文中的尺度變換時間tn和式(6)中的尺度變換函數應用到式(13)中，可得

(14)

對式(14)沿時間軸t和時延軸τ進行二維傅里葉變換，即為Sigmoid-LVD的定義。定義式為

(15)

3.2 參數估計方法

假設脈沖噪聲環境下的線性調頻信號為y(t)，則

y(t)=s(t)+n(t) ，

(16)

其中，s(t)為線性調頻信號，n(t)為Alpha穩定分布噪聲。信號經過Sigmoid函數處理后，即Sigmoid[y(t)]，再對其進行LVD變換，在中心頻率-調頻斜率域搜索峰值點即可完成參數估計。

在文獻[12]中使用Sigmoid函數時，假設信號全為實信號，在遇到復信號時，其能力可能會失效。筆者利用Sigmoid函數的性質4，在參數ω0中進行改變。在進行仿真實驗的時候，用Sigmoid函數處理信號后再除以它們的共軛，以此達到對復信號的參數估計。因為該運算包含在參數ω0中，根據性質4，其不會對信號造成失真。

4 仿真結果與分析

4.1 噪聲抑制能力分析

4.1.1 不同脈沖噪聲下對單分量線性調頻信號的檢測和參數估計性能分析

為了驗證所提算法在強脈沖噪聲下的檢測性能，該實驗分別在α=1.5和α=0.5的脈沖噪聲環境下進行仿真分析。信號參數為：幅度A=1，中心頻率f0=30 Hz，調頻斜率k=50 Hz/s，有效時間長度T=1 s，采樣頻率fs=512 Hz，RGSNR=-8 dB。

實驗結果如圖2所示。

圖2中的(a)、(b)和(c)分別表示α=1.5時，3種算法的檢測結果。從圖中可以看出FLOLVD和A-NAT-LVD受到噪聲影響，有一些很小的偽峰干擾，但還是能夠提取信號參數的，而Sigmoid-LVD明顯受噪聲影響較小，并且中心頻率和調頻斜率與實際值一樣，證明在α=1.5和RGSNR=-8 dB的脈沖噪聲下，Sigmoid-LVD要比 FLOLVD和A-NAT-LVD抑制噪聲能力強。

圖2中的(d)、(e)和(f)分別表示α=0.5時3種算法的檢測結果。可以很明顯地看出，FLOLVD湮沒在噪聲中，而A-NAT-LVD和Sigmoid-LVD仍然能夠準確地檢測和估計目標參數，并且與實際值一致。從圖2(d)～(f)可知，在強脈沖噪聲環境下Sigmoid-LVD的檢測能力超過FLOLVD，與A-NAT-LVD的效果基本一致。

4.1.2 不同廣義信噪比下對單分量線性調頻信號的檢測和參數估計性能分析

為了驗證所提算法在極低信噪比下的優越檢測性能，在不同廣義信噪比下進行仿真分析。設置脈沖強度α=0.5，除廣義信噪比以外，其他信號參數與節4.1.1的實驗相同。廣義信噪比分別為RGSNR=-8 dB和RGSNR=-15 dB。圖2中已經給出了RGSNR=-8 dB時3種算法的檢測結果圖，從圖2中(d)、(e)和(f)可以看出FLOLVD湮沒在噪聲中，而A-NAT-LVD和Sigmoid-LVD峰值點所對應的中心頻率和調頻斜率與實際值一致。由圖2(d)可得，在α=0.5，RGSNR=-8 dB時，FLOLVD已經失效，所以以下實驗不再給出RGSNR=-15 dB時FLOLVD的結果圖。

圖3描述了RGSNR=-15 dB時，Alpha穩定分布噪聲下線性調頻信號的A-NAT-LVD和Sigmoid-LVD的檢測結果。從圖中可以看出，A-NAT-LVD湮沒在噪聲中，而Sigmoid-LVD能夠產生明顯的尖峰，且與實際值相符。結合上節的實驗和本實驗可得，A-NAT-LVD僅是針對抑制強脈沖噪聲，在脈沖比較弱的時候其檢測能力降低。同時，在強脈沖中，處于極低信噪比的情況下，A-NAT-LVD的參數檢測和估計能力也不如Sigmoid-LVD。綜上可得，筆者所提的Sigmoid-LVD方法的抑制噪聲能力比FLOLVD和A-NAT-LVD的強。

(a) A-NAT-LVD (RGSNR=-15 dB)

4.1.3 不同脈沖噪聲下對雙分量線性調頻信號的檢測和參數估計性能分析

為了驗證所提算法對雙分量線性調頻信號的檢測能力，對雙分量線性調頻信號進行了仿真分析。設置脈沖背景噪聲α=1.5和α=0.5，以及RGSNR=-8 dB的Alpha穩定分布噪聲。信號參數與節4.1.1的實驗相同。圖4描述了不同Alpha穩定分布噪聲下雙分量線性調頻信號的檢測結果。

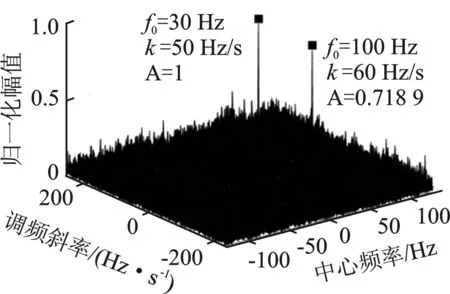
(a) FLOLVD(α=1.5)

圖4中(a)、(b)和(c)分別表示α=1.5，RGSNR=-8 dB時，雙分量線性調頻信號的FLOLVD、A-NAT-LVD和Sigmoid-LVD的檢測結果。從圖中可得3種算法都可以準確地進行參數估計，但是A-NAT-LVD中受到噪聲影響產生一些偽峰。

圖4中(d)、(e)和(f)分別表示α=0.5，RGSNR=-8 dB時雙分量線性調頻信號的FLOLVD、A-NAT-LVD和Sigmoid-LVD的檢測結果。FLOLVD被湮沒在噪聲中，而A-NAT-LVD和Sigmoid-LVD仍然能夠檢測出目標參數，并且中心頻率和調頻斜率與實際值一樣。為了進一步驗證所提算法的優越性能，增加了實驗對比。由于在α=0.5和RGSNR=-8 dB條件下FLOLVD算法已經失效，所以增加了α=0.5，RGSNR=-15 dB 時A-NAT-LVD和Sigmoid-LVD的檢測結果。如圖4(g)和(h)所示，A-NAT-LVD湮沒在噪聲中，Sigmoid-LVD受到噪聲影響有偽峰產生，但仍可進行參數估計。可見在雙分量線性調頻信號中，Sigmoid-LVD檢測參數估計能力仍然要高于FLOLVD和A-NAT-LVD的。

4.2 算法估計性能分析

為了驗證所提算法的檢測和參數估計性能，該實驗對3種算法進行了參數估計，給出了200次蒙特卡羅實驗所得的中心頻率和調頻斜率估計值的平均值。表1中脈沖噪聲α=1.5，RGSNR=-8 dB，表2中脈沖噪聲α=0.5，RGSNR=-15 dB，其余信號參數與節4.1.1的實驗相同。

從表1可以看出，在α=1.5的情況下，FLOLVD和Sigmoid-LVD能夠準確地對信號參數進行估計，與實際值一致，而A-NAT-LVD受到噪聲影響，其估計值有誤差。

表1 -8 dB下不同算法對線性調頻信號的參數估計值比較(α=1.5)

由于在α=0.5，RGSNR=-8 dB時，FLOLVD算法失效，所以表2中給出了α=0.5，RGSNR=-15 dB的情況下A-NAT-LVD和Sigmoid-LVD的估計值，可以得到Sigmoid-LVD的估計值要比A-NAT-LVD的估計值精確18%以上，再一次證明了A-NAT-LVD僅抑制強脈沖噪聲，在脈沖噪聲較弱的情況下，其參數估計能力下降；在強脈沖噪聲下處于極低信噪比時，其參數估計能力也嚴重下降。綜上，Sigmoid-LVD算法的參數估計能力要強于A-NAT-LVD。

表2 -15 dB下不同算法對線性調頻信號的參數估計值比較(α=0.5)

為了進一步驗證所提算法的檢測性能和參數估計性能，分別在不同廣義信噪比下和脈沖噪聲下進行仿真分析。除了廣義信噪比和脈沖噪聲外，其他信號參數與節4.1.1的實驗相同。圖5中(a)和(b)是在α=1.5時不同廣義信噪比下線性調頻信號的中心頻率和調頻斜率的估計誤差性能曲線，廣義信噪比的區間設置為[-15 dB，5 dB]，步長為1，每個廣義信噪比下都進行200次蒙特卡羅實驗。從圖5中可以看出，所提算法在[-15 dB，-12 dB]之間，隨著廣義信噪比的增大，均方根誤差急劇地減小，在-12 dB時均方根誤差為0。而A-NAT-LVD和FLOLVD的均方根誤差雖然也隨著廣義信噪比的增大在下降，但是下降趨勢不如Sigmoid-LVD，中心頻率均方根誤差在-10 dB時才為零，調頻斜率均方根誤差在-9 dB時為零。可見在參數相同的情況下，Sigmoid-LVD的抑制噪聲能力要強于A-NAT-LVD和FLOLVD，并且在有誤差的情況下所提算法的誤差要小于A-NAT-LVD和FLOLVD。圖5中(c)和(d)是當RGSNR=-8 dB時，不同脈沖強度下線性調頻信號的中心頻率和調頻斜率的估計誤差性能曲線，脈沖噪聲的區間設置為[0.5，2.0]，步長為0.1，每個脈沖噪聲下都進行200次蒙特卡羅實驗。從圖中可以得到所提算法在設置的脈沖噪聲區間內均方根誤差為零，可以準確地檢測和估計線性調頻信號的參數，而FLOLVD在[0.5，1.2]之間有誤差，中心頻率在α=1.2時誤差減小為零，調頻斜率在α=1.1時誤差減小為零。A-NAT-LVD在α=1.4時開始產生誤差，并且隨著脈沖噪聲的減弱，誤差越來越大，可得其僅在強脈沖噪聲下有效。從以上結果可得，Sigmoid-LVD的抑制噪聲能力優于A-NAT-LVD和FLOLVD，在強脈沖噪聲和極低信噪比下具有良好的魯棒性。

(a) α=1.5時中心頻率估計誤差

5 結束語

該文提出了一種在脈沖噪聲下對線性調頻信號進行參數估計的新方法——Sigmoid-LVD。首先引入了LVD的定義，同時介紹了非線性函數Sigmoid的性質，并加以推導，依據此性質，用Sigmoid函數來處理原始信號，再除以信號的共軛；然后根據LVD的定義對Sigmoid變換的對稱瞬時自相關函數沿時間軸t和時延軸τ進行二維傅里葉變換。仿真結果表明，Sigmoid-LVD不依賴于噪聲的先驗知識，能夠很好地抑制脈沖噪聲，在強脈沖噪聲和極低信噪比下擁有更高的參數估計精度，同時還可以實現對復信號的參數估計，有利于在信號處理中的應用。