基于SSAE-SVM的滾動軸承故障診斷方法研究

徐先峰，黃 坤，鄒浩泉，趙龍龍

(長安大學電子與控制工程學院，陜西 西安 710064)

0 引言

滾動軸承是廣泛應用于旋轉(zhuǎn)機械設備的核心器件，一旦發(fā)生故障，將對機械系統(tǒng)、工人生命安全和國民經(jīng)濟構成嚴重威脅。因此，對滾動軸承故障的精確診斷具有現(xiàn)實意義[1-3]。進入21世紀以來，深度學習和人工神經(jīng)網(wǎng)絡在滾動軸承故障診斷分類領域展現(xiàn)出巨大潛力。研究人員將多種具備監(jiān)督學習能力的深度學習算法應用于軸承故障診斷中[4]。Feng等[5]為提高傳統(tǒng)軸承故障診斷的有效性，提出了基于改進的量子人工蜂群算法的反向傳播神經(jīng)網(wǎng)絡診斷模型(improved quantum artificial bee colony-back propagation,IQABC-BP)，利用改進的量子蜂群算法進行量子蜂群計算，并解決了利用率低的問題。應用改進的量子蜂群算法對反向傳播(back propagation,BP)神經(jīng)網(wǎng)絡的初始權重、閾值和隱層數(shù)進行優(yōu)化，并將其應用于滾動軸承的故障診斷。試驗結(jié)果表明，IQABC-BP的收斂速度更快、故障診斷效果更好。然而，該方法并未考慮頻域的滾動軸承故障信號分析。為了在頻域分析滾動軸承故障特征，Liang等[6]提出了1種基于卷積神經(jīng)網(wǎng)絡(convolutional neural network,CNN)和頻譜圖的滾動軸承故障診斷方法。該方法利用快速傅里葉變換(fast Fourier transform,FFT)，從原始一維振動信號中提取頻率特征，并將其轉(zhuǎn)換為二維頻率頻譜圖輸入到CNN模型中，以實現(xiàn)滾動軸承的故障診斷。試驗結(jié)果表明，與傳統(tǒng)方法相比，該方法具有更優(yōu)良的精度和穩(wěn)定性。但是，該方法在解決標簽數(shù)據(jù)有限的無監(jiān)督或者半監(jiān)督學習問題上存在很大的局限性。李萌等[7]針對標簽數(shù)據(jù)有限的滾動軸承故障診斷問題，提出了基于堆棧稀疏自編碼(stacked sparse autoencoder,SSAE)的滾動軸承故障診斷方法。該方法利用SSAE網(wǎng)絡對原始信號進行特征提取，并利用Softmax分類器進行分類，實現(xiàn)滾動軸承故障診斷。試驗結(jié)果表明，該方法對解決無監(jiān)督學習問題具有明顯優(yōu)勢。

綜合分析深度學習模型在滾動軸承故障診斷領域的應用現(xiàn)狀，主流的故障診斷方法仍然是基于監(jiān)督學習的應用，即利用有標簽的數(shù)據(jù)來訓練模型。但是，現(xiàn)實中所獲得的數(shù)據(jù)集中，大部分為無標簽數(shù)據(jù)。如果要制作數(shù)據(jù)標簽，不僅費時費力，而且具有很大的隨機誤差。

本文在上述研究的基礎上，提出了1種基于SSAE和支持向量機(support vector machine,SVM)的堆棧稀疏自編碼-支持向量機(stacked sparse autoencoder-support vector machine,SSAE-SVM)的滾動軸承故障診斷方法。該方法在SSAE自適應特征學習網(wǎng)絡中加入貪婪算法逐層進行訓練，并使用反向微調(diào)算法實現(xiàn)誤差最小化，進而對滾動軸承故障頻域特征進行深層學習。最后，把5層結(jié)構的SSAE特征學習網(wǎng)絡的輸出輸入到SVM分類器中，以實現(xiàn)滾動軸承故障的準確分類。

1 基于SSAE的滾動軸承深層故障特征提取

1.1 堆棧稀疏自動編碼器原理

自動編碼器(autoencoder,AE)采用典型的對稱無監(jiān)督學習算法，通過反向微調(diào)算法最小化目標和輸出誤差[8]。AE結(jié)構包含輸入層、編碼層和輸出層3級網(wǎng)絡。AE結(jié)構如圖1所示。

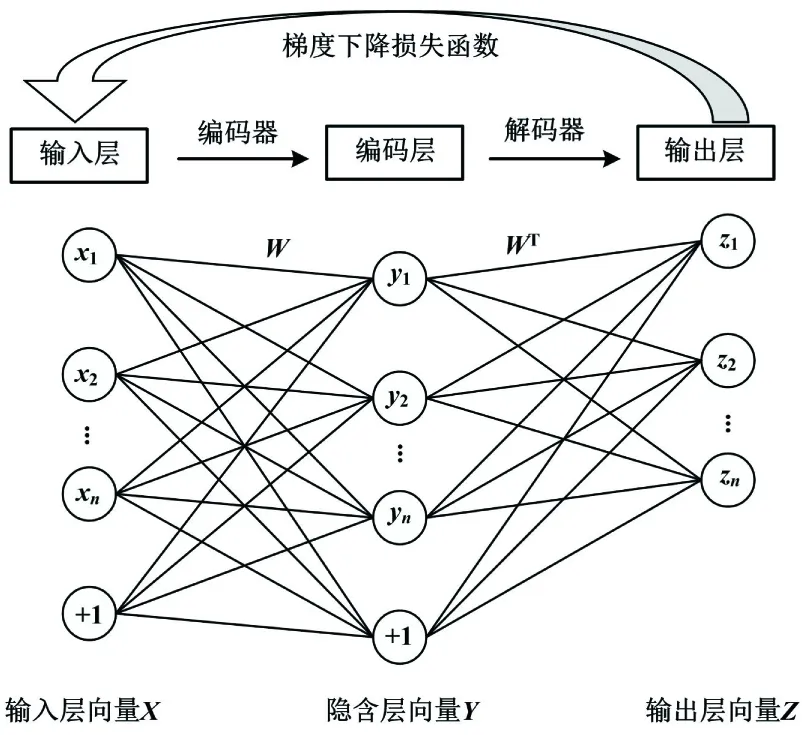
圖1 AE結(jié)構圖Fig.1 Structure diagram of AE

稀疏自動編碼器(sparse autoencoder,SAE)是在AE的基礎上增加了一些稀疏性約束，用于尋找一組超完備基向量，以便高效地表示樣本數(shù)據(jù)[9]。由于對隱藏層進行了稀疏性限制，SAE的學習能力得到了顯著增強，可以獲得更為簡單的信號表達方式。因此，該方法更容易獲取信號中的信息，以便對信號進行壓縮、編碼等加工處理。

SSAE是由多層稀疏自編碼器組成的神經(jīng)網(wǎng)絡模型。SSAE網(wǎng)絡結(jié)構如圖2所示。

圖2 SSAE網(wǎng)絡結(jié)構Fig.2 Structure of SSAE network

圖2中：X為輸入向量；Si為第i個(i=1,2,...,n)稀疏自動編碼器；hi為Si的輸出特征向量。

SSAE與自動編碼器類似，前向和反向訓練模式可以減小重構信號和輸入信號之間的偏差。將高維輸入數(shù)據(jù)轉(zhuǎn)換為低維特征，并經(jīng)過解碼過程中激活函數(shù)的重構成為輸出目標。編碼層輸出的編碼向量可以被視為對原始輸入信號的一種深層特征提取[10]。

①編碼過程：通過激活函數(shù)fθ()將樣本映射為編碼向量，如式(1)所示。

Y=fθ(WX+b)

(1)

式中：fθ()為Sigmoid激活函數(shù)；W為輸入層到隱含層的權值矩陣；b為隱含層閾值(偏置)向量。

②解碼過程：原始數(shù)據(jù)的矢量重構過程如式(2)所示。

Z=fθ(WTY+b′)

(2)

式中：WT為隱含層到輸出層的權值矩陣；b′為輸出層閾值(偏置)向量。

1.2 基于SSAE的滾動軸承深層故障特征提取

SSAE網(wǎng)絡的訓練過程包含前向網(wǎng)絡預訓練(無監(jiān)督方式)和反向微調(diào)(有監(jiān)督方式)2個過程。網(wǎng)絡的訓練過程中，輸入特征信號通過正向傳播和反向傳播2個階段循環(huán)地調(diào)整各層的參數(shù)，以提高神經(jīng)網(wǎng)絡的性能。SSAE前向網(wǎng)絡預訓練采用了貪婪算法[11]進行逐層訓練。貪婪算法逐層訓練過程如圖3所示。

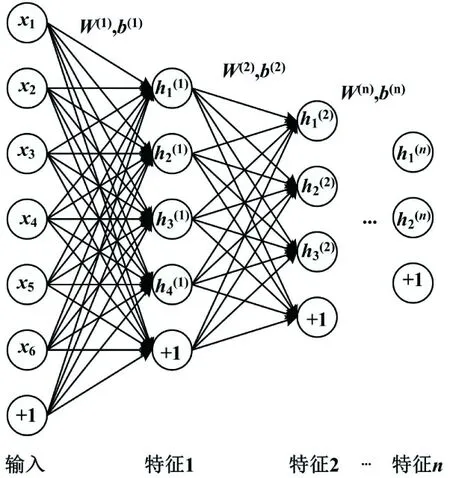
圖3 貪婪算法逐層訓練過程Fig.3 Layer-wise training process of greedy algorithm

由圖3可知，該算法訓練過程如下。首先，利用輸入的原始滾動軸承故障特征訓練SSAE神經(jīng)網(wǎng)絡的第一層稀疏自編碼器，得到參數(shù)權重W(1)和偏置b(1)。然后，在第一層網(wǎng)絡訓練結(jié)束之后，開始訓練第二層具有2個隱含層的網(wǎng)絡；將第一個SAE隱含層的輸出作為第二個SAE隱含層的輸入，得到第二層的參數(shù)權重W(2)和偏置b(2)。以此類推，把已訓練好的第(n-1)層的輸出作為第n層的輸入，獲得最后一層的參數(shù)權重W(n)和偏置b(n)。

SSAE的訓練過程可理解為調(diào)整其參數(shù)權重矩陣W和偏置b，使原始輸入與重構誤差的損失函數(shù)最小化。當重構目標與訓練樣本的相似度達到最高時，編碼矢量特征向量可被視為原始信號的最優(yōu)降維表達。其數(shù)學表達式為：

(3)

式中：xi為第i個神經(jīng)元對應的輸入向量；zi為第i個神經(jīng)元對應的輸出向量；l為神經(jīng)元個數(shù)。

在反向微調(diào)過程中，采用BP算法優(yōu)化和更新所有隱含層參數(shù)，以增強整個網(wǎng)絡的性能。部分訓練數(shù)據(jù)被選作整個網(wǎng)絡的監(jiān)督學習的輸入。誤差信號流反向傳播流程如圖4所示。

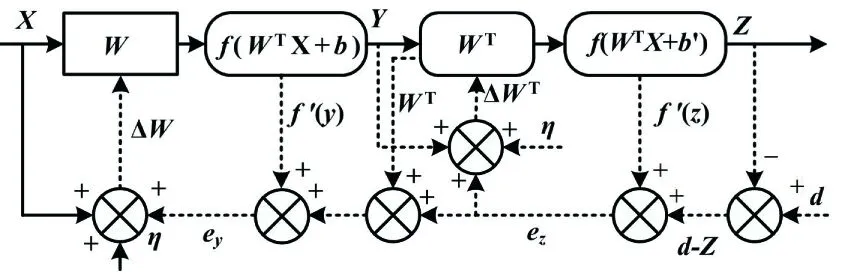
圖4 誤差信號流反向傳播流程Fig.4 Process of error signal flow back propagation

圖4中：ez和ey分別為輸出層和隱含層的誤差信號；η為學習率；ΔWT和ΔW分別為隱含層和輸入層的調(diào)整權值；f為各層的轉(zhuǎn)移函數(shù)，具有連續(xù)可導的特性；d為期望的誤差。

利用式(1)和式(2)，將BP誤差展開到輸入層：

(4)

(5)

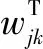
通過梯度下降法進行更新，取得合適的權值和偏置參數(shù)，使誤差E最小。對輸出層的權值參數(shù)進行調(diào)整：

(6)

式中：η為學習率。

反向?qū)﹄[含層的權值進行調(diào)整：

(7)

2 SVM分類器及構造方法

SVM是1種以統(tǒng)計學原理作為理論基礎的監(jiān)督學習方法，具有構造簡單、結(jié)構風險小、非線性問題處理能力佳、泛化性能好等優(yōu)點，在處理模式識別及回歸問題中展示了良好的性能[12]。本文選擇徑向基核函數(shù)作為SVM滾動軸承故障分類器的核函數(shù)，處理非線性問題。核函數(shù)表達式為：

(8)

SVM算法原來是專門針對二值分類問題所研究的。然而，要識別的滾動軸承故障類型遠不止2種。對此，解決方法是訓練多個二分類器來模擬多分類器。多分類器的構造方法主要有直接法和間接法。經(jīng)過SSAE深層特征提取器提取的特征在SVM分類器中進行分類。SVM分類器原理如圖5所示。

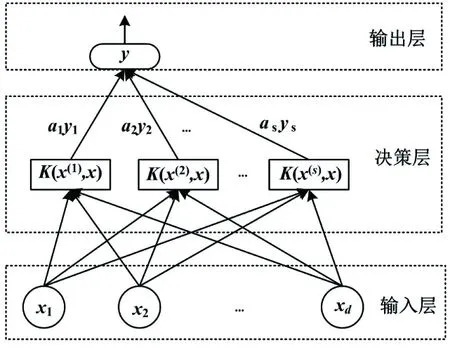
圖5 SVM分類器原理示意圖Fig.5 Schematic diagram of SVM classifier

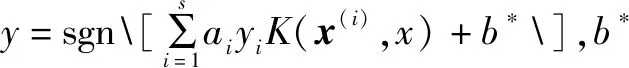
3 SSAE-SVM滾動軸承故障診斷模型

3.1 模型框架構建流程

SSAE-SVM滾動軸承故障診斷模型簡稱為SSAE-SVM模型。SSAE-SVM模型整體設計流程如圖6所示。

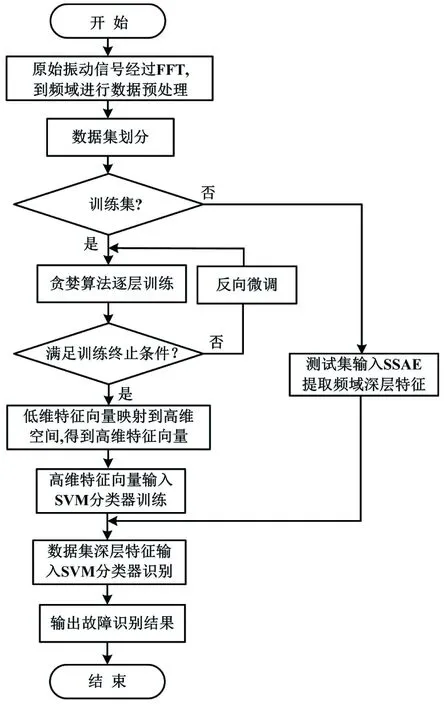
圖6 SSAE-SVM模型整體設計流程Fig.6 Overall design process of SSAE-SVM model

模型搭建流程主要包含數(shù)據(jù)處理、基于SSAE的滾動軸承故障特征自適應學習和基于SVM分類器的滾動軸承故障分類這3個核心內(nèi)容。

在模型的搭建過程中，激活函數(shù)fθ(z)選擇tanh激活函數(shù)，即：

(9)

式中：θ={W,b}為參數(shù)集合。

當fθ(z)接近1時，表示神經(jīng)元活躍；當fθ(z)接近-1時，表示神經(jīng)元被抑制。

3.2 試驗驗證

本文的試驗數(shù)據(jù)來自美國凱斯西儲大學滾動軸承數(shù)據(jù)中心。其數(shù)據(jù)集是學術界普遍使用的軸承故障診斷基準數(shù)據(jù)集[13]。美國凱斯西儲大學滾動軸承數(shù)據(jù)集采集系統(tǒng)主要包括風扇端軸承SKF6203、1.5 kW的電機、驅(qū)動端軸承SKF6205扭矩傳感器和編碼器等部件。本文選用美國凱斯西儲大學滾動軸承驅(qū)動端和風扇端軸承數(shù)據(jù)作為試驗數(shù)據(jù)，檢驗所建立的SSAE-SVM模型的性能。該試驗所用數(shù)據(jù)為48 kHz的驅(qū)動端軸承SKF6205數(shù)據(jù)：選擇10 000個數(shù)據(jù)樣本，按照7∶3的比例設置訓練集和測試集樣本數(shù)量[14]。

試驗數(shù)據(jù)樣本劃分如表1所示。

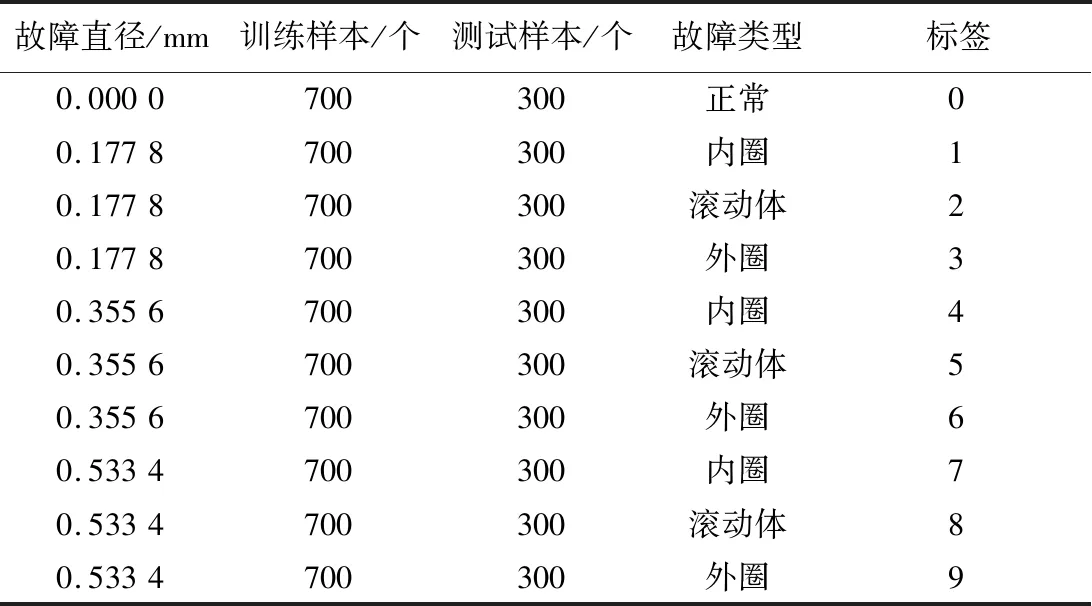
表1 試驗數(shù)據(jù)樣本劃分Tab.1 Division of experimental data samples

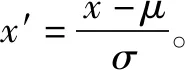
①模型訓練的收斂速度和準確率。

利用訓練樣本，檢驗SSAE-SVM模型與對比模型在7 000個訓練集樣本上的準確率和收斂速度。根據(jù)第5次、第10次、第20次、第30次、第50次、第80次、第100次、第120次、第150次迭代所對應的準確率，繪制準確率折線。不同訓練次數(shù)的模型準確率對比如表2所示。

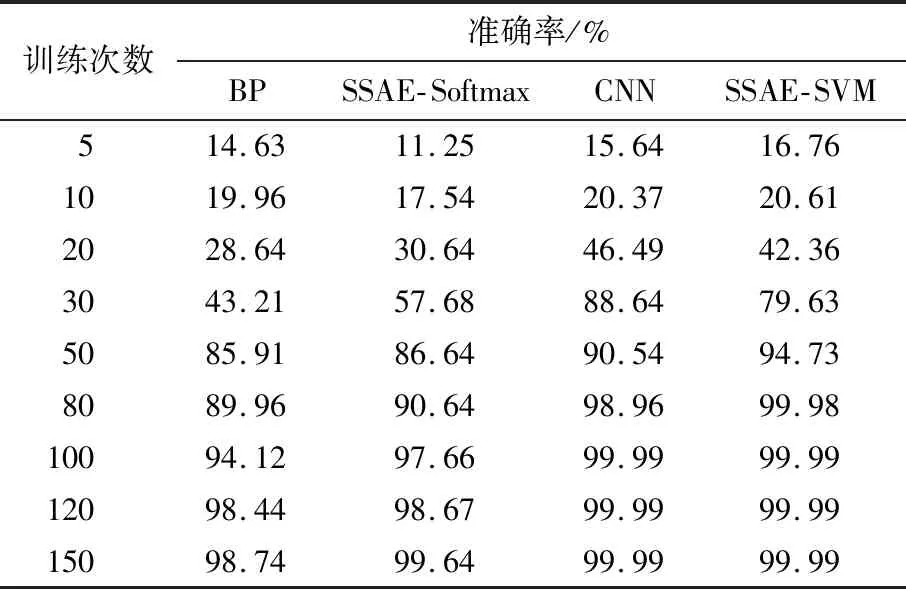
表2 不同訓練次數(shù)的模型準確率對比Tab.2 Comparison of model accuracy with different training times

由表2可知：SSAE-SVM模型和CNN模型的收斂速度比SSAE-Softmax模型和BP模型更快；SSAE-SVM模型的準確率在訓練次數(shù)達到80次后穩(wěn)定在99.9%以上。

②SSAE-SVM模型和對比模型的性能對比。

SSAE-SVM模型與3個對比模型使用測試集分別試驗10次。不同測試次數(shù)的模型準確率對比如圖7所示。

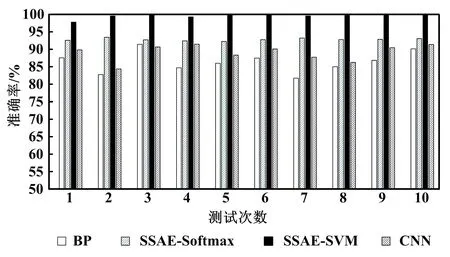
圖7 不同測試次數(shù)的模型準確率對比Fig.7 Comparison of model accuracy with different test times

由圖7可知，SSAE-SVM模型比SSAE-Softmax模型、BP模型和CNN模型的滾動軸承故障診斷準確率更高，平均準確率可達99.74%。

③迭代次數(shù)對模型準確率的影響。

為了檢驗迭代次數(shù)對滾動軸承故障診斷性能的影響，將迭代次數(shù)分別設置為5次、10次、20次、50次、100次，利用測試集進行10次試驗，然后取平均值。不同迭代次數(shù)的模型準確率對比如圖8所示。

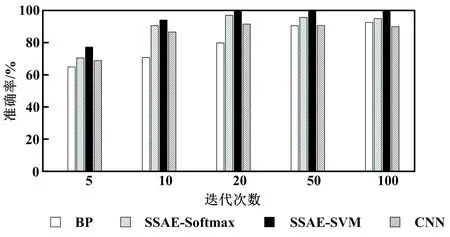
圖8 不同迭代次數(shù)的模型準確率對比Fig.8 Comparison of model accuracy with different iteration times

由圖8可知，所有模型的滾動軸承故障診斷的準確率均受到了迭代次數(shù)的影響。尤其當?shù)螖?shù)小于10時，3個對比模型的故障診斷準確率均有較大的損失。BP模型在迭代次數(shù)大于50后才達到90%左右。CNN模型在處理大量有監(jiān)督學習訓練樣本時具有很高的準確率，但在少量有監(jiān)督學習樣本中的性能較差。相較于3個對比模型，SSAE-SVM模型準確率更高、穩(wěn)定性更強，因而更具優(yōu)越性。

4 結(jié)論

本文基于無監(jiān)督學習方法，提出了基于SSAE-SVM的滾動軸承故障診斷方法，解決了現(xiàn)有算法過度依賴有標簽故障數(shù)據(jù)的問題。首先，利用SSAE進行無監(jiān)督式深層學習獲得滾動軸承故障的高維深層特征，構建5層SAE堆疊而成的SSAE自適應學習網(wǎng)絡。然后，使用貪婪算法逐層訓練和反向微調(diào)算法對其進行改進。最后，將深層特征向量輸出至SVM監(jiān)督學習分類器，實現(xiàn)滾動軸承故障分類。采用美國凱斯西儲大學滾動軸承數(shù)據(jù)集將SSAE-SVM滾動軸承故障診斷模型分別與SSAE-Softmax的軸承故障診斷模型、基于BP神經(jīng)網(wǎng)絡的軸承故障診斷模型和基于CNN神經(jīng)網(wǎng)絡的滾動軸承故障診斷模型進行對比試驗。試驗結(jié)果表明，本文所提模型的準確率更高、收斂速度更快，表明應用無監(jiān)督學習建立軸承故障診斷模型將成為軸承故障診斷的重要發(fā)展方向之一。