基于持續同調的脈沖渦流提離距離測量方法
段淑玉 宋 韻 武新軍
(華中科技大學機械科學與工程學院)
在石油化工與新能源行業,部分管道、容器等構件有保溫需求,外部帶有包覆層,這些構件在長期使用過程中,內壁受內部介質沖刷可能發生流動加速腐蝕,而包覆層多孔易吸水、含有硫物質等,容易在外壁形成電化學腐蝕。 當腐蝕造成的壁厚減薄達到一定程度時,可能引發安全事故,因此需對帶包覆層管道壁厚減薄情況進行定期檢測。
目前常用的無損檢測方法大多需拆卸包覆層[1],盡管射線檢測可以實現不拆除包覆層檢測,但易受包覆層中雜物的干擾,難以準確檢測腐蝕情況,檢測速度慢、成本高、對環境有污染而且存在安全隱患[2]。
脈沖渦流檢測(Pulsed Eddy Current Testing,PECT)技術可以實現在完全不拆卸包覆層的情況下對金屬管道內外壁的腐蝕情況進行檢測,檢測經濟成本低、人力成本低且安全性好,已廣泛應用于石油化工行業帶包覆層鐵磁性管道壁厚減薄的檢測[3]。 由于包覆層厚度變化或探頭運動引起的提離噪聲會嚴重影響脈沖渦流檢測精度,抑制提離效應,因此提高帶包覆層金屬構件厚度的測量精度是PECT研究的熱點。 目前,抑制提離效應的方法主要分為3類: 一是通過陣列式傳感器結構消除提離變化的影響[4];二是尋找與提離無關的信號特征量,包括晚期信號衰減率、提離交叉點及頻域相位等[5~7];三是提離效應補償方法,通過研究提離對檢測信號的影響,進而給出補償方案。 相比于尋找與提離無關的特征量,研究測量提離距離進而給出補償的方法顯然更有意義。Fu Y W等提出一種基于檢測信號傅里葉變換動態軌跡的檢測方法,從提離軌跡中識別出缺陷軌跡,并通過將缺陷軌跡移動到零提離點的方法有效減小提離效應[8];Huang P J等利用偏最小二乘法建立了提離預測模型,在測量提離距離的基礎上提出了一種檢測多層導電結構內部狀態的方法[9]。 這些提離補償方法都是針對提離距離小于5 mm的薄涂層情況,對于包覆層厚度較大的情況(提離距離超過50 mm)則未必適用。因此,筆者針對大提離距離的測量,從拓撲學角度分析信號特征,提出一種基于持續同調特征條形碼的不銹鋼板脈沖渦流大提離距離測量方法。
1 持續同調理論
持續同調 (Persistent Homology,PH) 源于Morse理論[10],在拓撲空間的持續變化中,通過單純復形構造同調群,再計算同調群得到拓撲不變量,如貝蒂數(Betti Number),以此描述拓撲空間的幾何結構特征和演化規律,是拓撲數據分析中應用最為廣泛的技術。
1.1 單純形、單純復形和Rips復形
單純形是代數拓撲中最基本的概念, 持續同調所適用的空間由各種維數的單純形所構造。
如圖1所示,低維單純形中,0維單純形是點,1維單純形是線段,2維單純形是三角形,3維單純形是四面體。 高維單純形則是它們的高維類似物。 單純復形由單純形組合而成,是研究拓撲不變量的基礎。 圖1e所示的單純復形由1個1維單純形、1個2維單純形和1個3維單純形組成, 單純復形的維數等于構成該復形的單純形的最大維數,因此圖1e為3維單純復形。
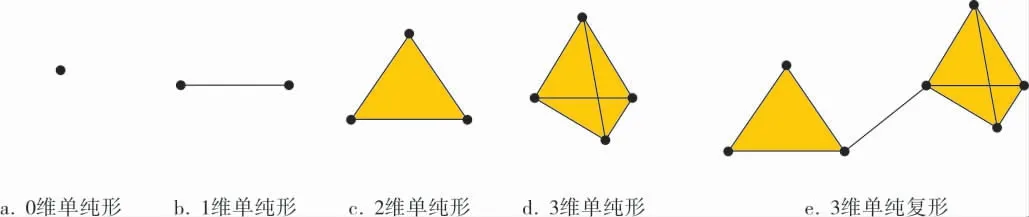
圖1 單純形和單純復形
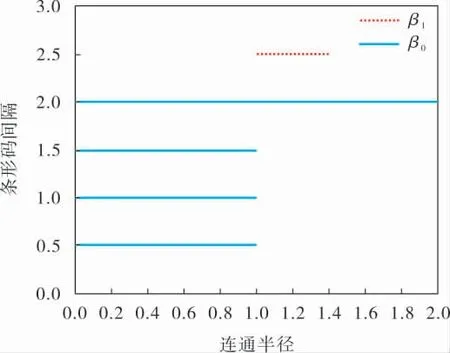
采用持續同調理論提取脈沖渦流檢測信號中與提離有關的特征量,其中重要的一步是為2維點云構建復形過濾流(Filtration Complex)。 Rips復形是構建復形過濾流最常用的方法之一。 給定點集X?Rn,設連通半徑r≥0且r∈R,對于x,y∈Rn,定義d(x,y)為點x到點y的距離。 如果k維單純形[x0x1… xk]滿足d(xi,xj)≤r(0≤i 對于拓撲空間Z, 同調給出了每個維數k=0,1,2,…的向量空間Hk(Z)。 Hk(Z)的維數稱為Z的k維貝蒂數,記為βk,是一組重要的拓撲不變量。β0表示拓撲結構中的連通分支數,β1表示1維“孔”的個數,β2表示2維“洞”的個數,依此類推。 對點云拓撲空間構造Rips復形, 隨著連通半徑r持續不斷變化,點云的拓撲不變量——貝蒂數記錄復形從產生到消亡的過程,即為持續同調。 2維點云持續同調計算示例如圖2所示,即分別以4個點為圓心,以r/2為半徑畫圓,其中4個點的坐標分別為(1,2)、(2,2)、(1,1)、(2,1);當r<1.000時4個圓彼此分離(圖2a), 故β0=4,β1=0; 當r增加至1.000時4個圓兩兩相切,連線相切圓的圓心,只剩1個連通分支,并形成1個1維孔(圖2b),故β0=1,β1=1;r繼續增大至1.414時,4個圓相交,1維孔被填滿(即孔消亡),連通分支數依然為1(圖2c),故β0=1,β1=0。 圖2 持續同調過程 持續條形碼(Persistent Barcode,PB)圖是持續同調結果的可視化工具[11], 描述貝蒂數的變化。 圖3為圖2持續同調的PB圖,實線條形碼表示連通分支數即β0, 虛線條形碼表示1維孔數即β1。條形碼的左端點表示孔洞產生時間,右端點表示孔洞消亡時間,條形碼的長度代表孔洞壽命。 實際應用中,孔洞產生時間和消亡時間與連通半徑對應,故PB圖中橫坐標一般為連通半徑,縱坐標為條形碼間隔。 圖3 持續同調的PB圖 采用自研的HPEC-B型帶包覆層非鐵磁金屬構件脈沖渦流檢測儀搭建實驗平臺(圖4)。 試件材料選用管道中廣泛使用的非鐵磁性304不銹鋼,平板試件尺寸500 mm×500 mm,厚度分別為18、21、24、27、30 mm。 提離距離從60 mm開始,間隔20 mm,最大140 mm。 圖4 脈沖渦流檢測實驗平臺 單對數坐標系下18、30 mm厚度的不銹鋼板檢測信號如圖5所示,可以看出,各信號先重合后分離;在衰減段,不同提離距離信號的衰減速度不同,提離距離越大,衰減速度越快,因此提離距離變化反映在信號衰減速度上。 圖5 不同厚度不銹鋼板在不同提離距離的脈沖渦流檢測信號 由圖5可知,在衰減段,脈沖渦流檢測信號的電壓及其衰減速度共同反映提離距離對檢測信號的影響。PECT信號衰減速度可以用各點鄰域擬合直線的斜率表征,故以PECT信號電壓值為橫坐標、各點斜率為縱坐標,構造2維點云拓撲空間,該空間拓撲性質可表征PECT信號特征。 30 mm厚度的304不銹鋼板不同提離距離PECT信號構造的點云如圖6所示, 其中鄰域長度M=7。 為了便于區分點云空間,不同提離距離對應離散點云用曲線相連。 由圖6可知,點云拓撲結構特征體現了提離距離對檢測信號的影響。 圖6 30 mm厚度不銹鋼板PECT信號構建的點云 對圖6點云進行持續同調計算, 取其0維貝蒂數β0繪制條形碼圖。 18、30 mm厚度不銹鋼板提離距離60、140 mm點云對應的條形碼圖如圖7所示。 條形碼圖中頂部的條碼最長,理論上是無限長, 表示最終點云中所有復形形成1個單連通分支。 圖中紅色虛線標識第2個最長條形碼對應的連通半徑,也即第2長條形碼長度,表示點云在連通半徑增至該值時點云中的復形形成1個單連通分支。 對比圖7a、b和圖7c、d可以看出, 相同厚度不同提離距離對應的第2長條形碼長度明顯不同; 對比圖7a、c和圖7b、d可以看出,相同提離距離下,板厚對第2長條形碼長度影響較小。 圖7 18、30 mm厚度及60、140 mm提離距離對應點云的0維貝蒂數條形碼 對于所有檢測信號構造的點云,利用持續同調算法獲取其0維貝蒂數, 繪制條形碼圖。 板厚18、21、24、27、30 mm, 提離距離60、80、100、120、140 mm的點云對應第2長條形碼的連通半徑(即第2長條形碼長度)如圖8所示,可見,第2長條形碼長度幾乎不受板厚影響, 只與提離距離有關,因此將第2長條形碼長度作為表征提離距離的特征量,即特征條形碼。 選擇不同板厚第2長條形碼長度的平均值與提離距離建立特征條形碼-提離距離對應關系,采用冪函數進行擬合,結果如圖8中的實線所示,擬合優度大于0.99。 圖8不同板厚和提離距離第2長條形碼長度及其擬合曲線 選取特征條形碼BarcodeLen 與提離距離Liftoff的擬合曲線可得標定曲線公式: 交換式(1)的自變量和因變量,可得標定方程式: 對1個PECT信號進行處理后, 得到特征條形碼,代入式(2),計算得到提離距離。 將所有PECT信號經持續同調處理得到的特征條形碼依次代入式(2),得到對應的提離距離,見表1,可以看出,提離距離標定結果的相對誤差為±6.00%,說明基于持續同調的特征條形碼可以作為PECT信號表征提離距離的特征量。 表1 不同板厚、提離距離下的PECT信號處理所得提離距離測量結果及其相對誤差 筆者提出一種基于持續同調特征條形碼的不銹鋼板脈沖渦流提離距離檢測方法。 首先,將檢測信號幅值與信號中各點鄰域擬合直線的斜率組合構建2維點云;其次,對點云進行持續同調計算,獲取其表征點云連通分支數的0維貝蒂數,并繪制條形碼圖;最后,提取條形碼圖中第2長條形碼長度作為特征量,該特征量與提離距離以冪函數擬合,建立特征條形碼-提離距離標定曲線。分析結果表明:當提離距離在60~140 mm、板厚大于18 mm時, 該特征量所表征提離距離的相對誤差為±6.00%。1.2 同調、持續同調和持續條形碼

2 基于持續同調的提離距離測量方法
2.1 實驗設置及信號



2.2 構建PECT信號的拓撲關系



2.3 基于持續同調提取點云拓撲特征量


2.4 實驗結果分析




3 結束語

