巧用數學思想,提升數學思維和素養
眭亞燕 沈秋萍




數學思想方法揭示概念、原理、規律的本質,是溝通基礎知識與能力的橋梁。通過學習平面圖形的認識(一),我們了解了線段、射線、直線的概念、性質以及三者間的關系,掌握了角、余角、補角、對頂角的概念及相關計算,認識了平行和垂直。通過學習平面圖形的認識(二),我們對直線和角的關系繼續進行了深入研究,同時了解了圖形的平移的特征并學習了三角形的入門知識。下面,我們以“線段”“角”為例,談談如何巧用數學思想解決問題。
一、數形結合思想
數形結合思想是根據數與形之間的對應關系,通過數與形的相互轉化來解決問題的數學思想。
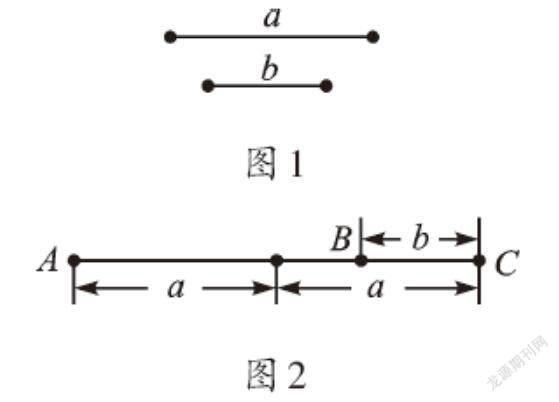
如圖1,已知線段a、b,求圖2中線段AB的長。
求線段AB的長,即求兩點之間的距離(數)。這個距離是一個數,而已知條件是圖形,這就需要我們正確地識別圖形(形),數形結合著思考。AB的長為2a-b。
二、方程思想
方程思想的本質即從問題的數量關系入手,運用數學語言將問題中的條件轉化為數學模型(方程),然后通過解方程(組)來使問題獲解。方程思想在解決線段問題的時候是一個很重要的工具。
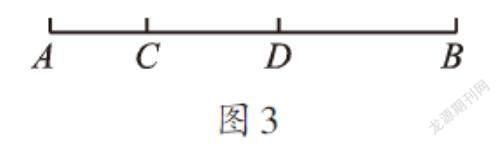
已知,如圖3,點C、D在線段AB上,且AC∶CD∶DB=2∶3∶4,如果AB=18,那么線段AD的長是多少?
根據已知條件中的比值,設合理的未知數,列正確的方程,是解決本題的關鍵。因為AC∶CD∶DB=2∶3∶4,故可設AC=2x,CD=3x,DB=4x,則AB=9x。又因為AB=18,所以9x=18,解得x=2,故AD=2x+3x=5x=10。
三、整體思想
整體思想就是從問題的整體性質出發,對問題的整體結構進行分析,發現問題的整體結構特征,用“集成”的眼光,把某些式子或圖形看成一個整體,把握它們之間的關聯,有目的、有意識地進行整體處理的思想。
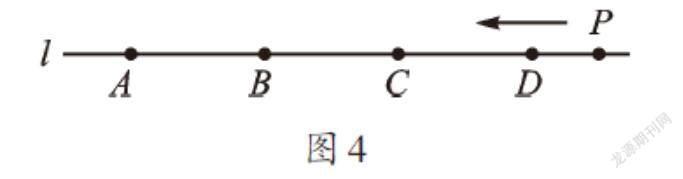
例如,如圖4,有一種電子游戲,電子屏幕上有一條直線,直線上有A、B、C、D四點。點P沿直線l從右向左移動,當點P與A、B、C、D四點中的至少兩個點距離相等時,就會發出警報,則直線l上會發出警報的點P最多有 個。
利用整體思想去思考線段的總條數是一種巧妙的辦法,可以減去不必要的討論與分類。由題意知,當P點經過任意一條線段中點的時候會發出警報,這時,我們只要數出線段總條數即可。因為圖中共有6條線段:DC、DB、DA、CB、CA、BA,所以發出警報的點P最多有6個。
四、化歸思想(化未知為已知)
化歸思想的本質在于將未知的、陌生的、復雜的問題通過演繹、歸納,轉化為已知的、熟悉的、簡單的問題。
如圖5,C、D是線段AB上的兩點,E是AC的中點,F是BD的中點,若EF=m,CD=n,則AB= 。
我們可以利用中點的性質轉化線段之間的倍分關系。在不同的情況下,靈活選用中點性質的表示方法,有利于提高解題的簡潔性。因為AE=EC,FB=FD,所以AB=AE+FB+EF=EC+FD+EF=EF-CD+EF=2m-n。
五、從特殊到一般的思想
從特殊到一般,即先觀察一些特殊的事例,然后分析它們具有的共同特征,最后做出一般的結論。從簡單情形中認識復雜的事物,能使抽象的數學問題變得更簡單,從而破解問題,乃至發現規律。
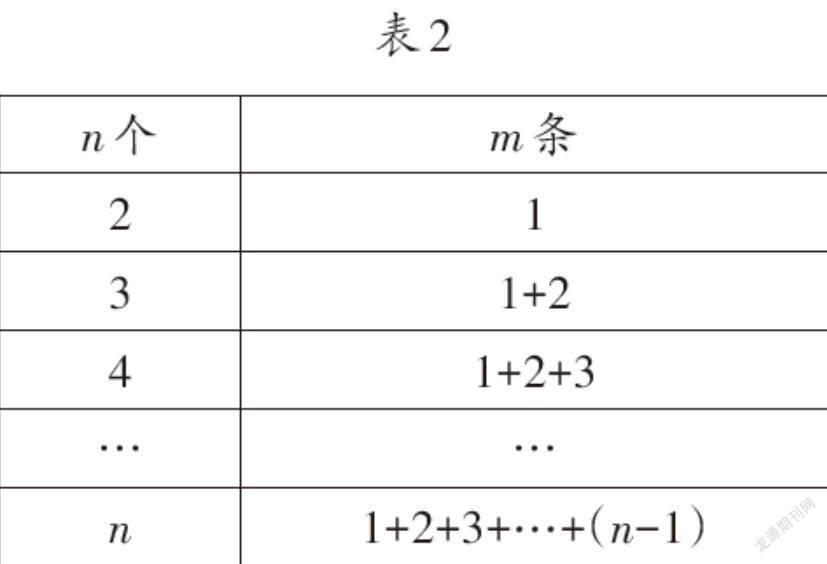
例如,一條直線上有若干個點,以任意兩點為端點可以確定一條線段,線段的條數與點的個數之間的對應關系如表1所示。請你探究表內數據間的關系,根據發現的規律,求表中p和q的值。
求p和q的過程,就體現了“從特殊到一般”的思維探索過程。我們設線段有n個點,分成的線段有m條,可以發現表2中的規律。從特殊到一般,找到規律是關鍵。
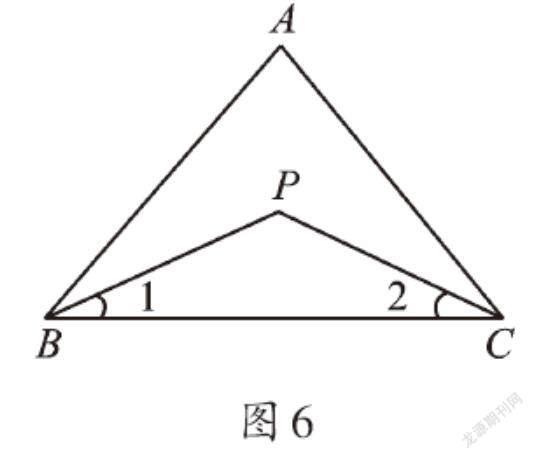
再如,如圖6,在△ABC中,∠A=80°,BP、CP分別平分∠ABC和∠ACB。(1)求∠P的度數;(2)如果將條件“∠A=80°”改為“∠A=α”,∠P的度數如何表示?
這里的第一問中,∠A=80°,∠A是具體的度數,同學們可以很容易地理清解題思路,得到∠P=130°。而第二問中,∠A=α,特殊的80°換成了一般化的α,此時方法不變,體現了解法的一般性和結論的一般性,得到∠P=90+[α2]。我們還可以將圖形一般化,將三角形變成四邊形。同學們,你能用類似的方法,把這個一般化問題獨立解決嗎?
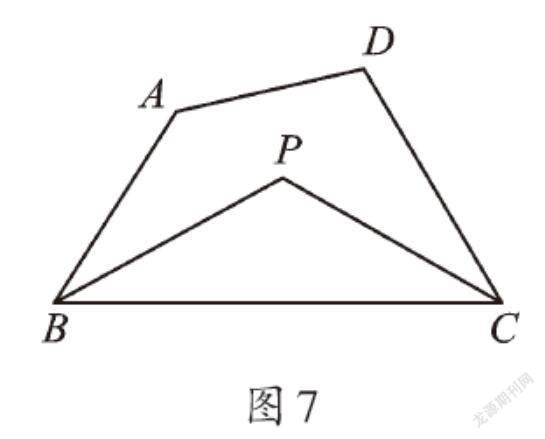
如圖7,在四邊形ABCD中,PB平分∠ABC,PC平分∠DCB,∠A+∠D=α,求∠P的度數。
六、建模思想
數學語言作為數學理論的基本構成成分,具有“高度的抽象性、嚴密的邏輯性、應用的廣泛性”。簡單地講,數學語言科學、簡潔、通用。用數學語言描述的事物就稱為數學模型。有時將實際問題抽象成數學模型來解決,會更方便。
例如,往返于甲、乙兩地的火車,中途要停靠三個站,則有 種不同的票價(來回票價一樣),鐵路公司需準備 種車票。
本題的實質是問共有多少條線段。我們可以從這個生活問題中抽象出數學模型——數線段,運用數學知識解決生活中的票價與票種問題。因為中間有3個站點,所以相當于一條直線上共有5個點,由表2的規律可知共有10條線段,因此共有10種不同的票價。有多少種車票是要考慮順序的,10×2=20,故共有20種車票。
七、類比思想
類比思想是我們學習道路上偉大的引路人。類比揭示了數學知識間的關系,能讓我們感悟數學思想和方法的內在聯系,升華思維,創造性地解決問題。
例如,已知△ABC和四邊形ABCD,我們能否分別將它們分成面積相等的四個部分?同學們在學習了三角形的中線、角平分線、高之后,不難發現,三角形的中線具有平分三角形面積的性質。因此,我們只需要先作一條三角形中線把三角形面積二等分,再用同樣的方法繼續將兩個三角形分別二等分即可。那四邊形怎么分呢?我們可以利用類比思想,將四等分四邊形面積的問題轉化為四等分三角形面積的問題,構造相應的三角形即可。
八、分類思想
當一個問題因為某個量或某個圖形的情況不同而有可能引起結果不同時,我們需要對這個量或圖形的各種情況進行分類討論。分類討論是一種重要的思想方法,更是一種解題策略。分類的原則是不重不漏。
例如,已知點P是射線AB上一點,當[PAPB]=2或[PAPB]=[12]時,稱點P是射線AB的強弱點。若AB=6,P是射線AB的強弱點,則PA= 。
求PA的距離,需要我們對點P的位置進行分類討論(當點P在點B右側時和當點P在點B左側時),我們可以畫出相關圖形進行求解。求得PA=2或4或12。
再如,已知直線AB∥CD,點P不在直線AB、CD上,連接PB、PD,則∠ABP、∠CDP、∠BPD有何數量關系?為什么?
對于七年級的我們來說,本題沒有相關的圖形,難度較大。同學們不妨自己動手畫出圖形,思考∠ABP、∠CDP、∠BPD這三個角的大小。結果出現的情況是唯一的嗎?顯然不是。我們可以按點P的位置分類討論。情況1:點P在直線AB、CD之間。(1)點P在直線BD的左側時,∠BPD=∠ABP +∠CDP;(2)點P在直線BD的右側時,同理可解。情況2:點P在直線AB、CD之外。希望同學們能用類比思想,按照“觀察→操作→思考→說理”這個流程,一步一步去解決問題。
同學們,數學的精神和數學中的思維方法、研究方法、推理方法、看問題的方式等,會在我們的生活、學習中隨時隨地發生作用,使我們終身受益。希望同學們在日后的學習或者生活中,能領悟到這句話的內涵,在數學的道路上越走越遠。
(作者單位∶江蘇省常州市新北區浦河實驗學校,江蘇省常州市田家炳初級中學)

