徑向壓縮碳納米管的電子輸運性質*

林旖旎 馬立? 楊權? 耿松超 葉茂盛 陳濤 孫立寧

1) (上海大學機電工程與自動化學院,上海 200072)

2) (蘇州大學,機器人與微系統研究中心,蘇州 215021)

研究徑向壓縮形變對碳納米管電子輸運性質的影響對搭建微納碳基電子器件具有重要意義.本文利用分子動力學模擬方法研究了碳納米管與金屬界面接觸構型,得出碳納米管徑向壓縮形變的規律.模擬結果表明:碳納米管在水平接觸金屬表面后,其穩定狀態下的徑向壓縮形變大小會受接觸長度、管徑大小、金屬種類和片層數量的影響.基于緊束縛密度泛函理論和非平衡格林函數結合的第一性原理,系統地研究了不同直徑、手性、片層、徑向壓縮形變碳納米管的電子輸運性質.研究表明:金屬性單壁碳納米管的電流呈線性增長趨勢,且電流-電壓的大小只與偏壓有關,與直徑大小無關;當其存在徑向壓縮形變時,電流在大偏壓下增長趨勢減緩,甚至會出現平臺效應.半導體性單壁碳納米管的導通電流隨著徑向壓縮形變的增加而減小,電流-電壓曲線逐漸從半導體特性向金屬特性轉變.隨著徑向壓縮形變的增加,雙壁碳納米管的電流-電壓曲線變化規律與金屬性單壁碳納米管的電流-電壓曲線變化規律一致,但在相同偏壓下,雙壁碳納米管的電流比單壁碳納米管的電流高1倍;三壁碳納米管的電流-電壓曲線存在較大的振蕩波動.

1 引言

碳納米管 (carbon nanotube,CNTs)具有優越的電子輸運及物理學等特性[1?5],自1991年被發現以來一直是新型材料領域研究的熱點[6],在納米碳基電子器件[7?9]和微納集成電路等方面有著廣泛的應用前景.彈道運輸特性的碳納米管可以代替傳統金屬導線,承載高出幾個數量級的電流,是納米電子器件和微納電路的理想導線,由半導體性碳納米管作為溝道材料組裝成的場效應晶體管[10?12]具有優異的開關比,可以取代傳統硅基場效應晶體管來延續摩爾定律的發展.

單壁碳納米管分為金屬型和半導體型,雙壁碳納米管根據其內壁和外壁電學特性的不同呈現出不同的性質,單壁、雙壁碳納米管作為基本單元經常被用于研究碳納米管電子輸運特性的研究[13?16].Wen等[17]制備了多壁碳納米管填充的SiO2基復合材料,討論了多壁碳納米管微電流網絡中遷移和跳躍電子的輸運性質,并探究了多壁碳納米管含量和溫度對電子輸運和電導率的影響.利用密度泛函理論結合非平衡格林函數計算方法,Berdiyorov等[18]研究了碳納米管包封對一維同素異形體碳炔鏈電子輸運性質的影響,碳納米管尺寸越小,碳炔結構的變化越明顯,導致電子輸運能力強烈降低;Algharagholy[19]研究了缺陷碳納米管的電子性能,缺陷的存在導致了高度無序的絕緣結構,隨著缺陷長度的增加,碳納米管電子輸運性質受到這種結構抑制的影響越嚴重;Teichert等[20]研究了碳納米管中缺陷導致的長程變形對其電子輸運性質的影響;Ohnishi等[21]通過比較金屬碳納米管變形后的電子態和幾何結構,分析了單軸壓縮應變對電子輸運性質的影響;Srivastava等[22]計算了由金屬和半導體單壁碳納米管組合而成的(5,4) @ (9,9),(4,4) @ (10,9),(5,4) @ (10,9)雙壁碳納米管的電子透射系數,使單壁碳納米管以合適的形式組合成雙壁碳納米管,為設計場效應晶體管、邏輯門和其他納米器件提供了基礎.采用密度泛函理論和分子動力學(MD)計算方法,Espinosa-Torres等[23]計算了一系列小直徑的碳納米管(扶手椅型和鋸齒型)和26種雙壁碳納米管組合的電子結構性質,證明了系統的電子結構性質決定了電子通過碳納米管界面輸運的能力.在組裝納米電子器件過程中,碳納米管與金屬表面之間存在范德瓦耳斯力,范德瓦耳斯力會使得碳納米管產生徑向壓縮形變[24],而徑向壓縮形變會影響碳納米管自身的電子結構和電子輸運能力[25?28],但是目前缺乏有效可靠的研究詳細闡明這些問題.

本文基于經典分子動力學研究碳納米管與金屬表面接觸而產生徑向壓縮形變的行為,利用緊束縛密度泛函(DFTB)方法探究碳納米管在不同徑向壓縮形變下的電子輸運特性,旨在揭示碳納米管的徑向壓縮形變對電子輸運特性的影響及其變化規律,為設計制作基于碳納米管的納米電子器件提供理論依據.

2 模型及計算方法

本文使用分子動力學方法模擬多壁碳納米管與金屬接觸過程,選取直徑為8.14和14.92 ?的單壁碳納米管(6,6),(11,11)及不同片層且直徑為14.92 ?的多壁碳納米管,搭建厚度為15 ?的金、鋁、鉑(1,0,0)晶格來構成57.68 ? × 57.68 ? ×75.77 ?的超胞體.選用COMPASS力場、正則系綜(NVT)來進行碳納米管與金屬界面之間的分子動力學模擬.為了得到較為精確的結果,截止距離設置在15.5 ?,總模擬時間設置為100 ps,計算步長為1 fs,每1000步輸出一次.分子動力學模擬的基本原理是假定所有粒子遵循牛頓運動力學規律,求解多原子相互作用的牛頓方程,通過相互作用勢能來體現體系的量子行為.各粒子間作用力通過對勢能函數求導得出:Fi??iU,其中U為分子勢能,?為哈密頓算子.本文使用范德瓦耳斯能差值以及結合能來表征碳納米管與金屬表面的接觸強度.結合能定義為EBindingETotal?ECNT?EMetal,其中ETotal為碳納米管與金屬表面體系的總能量,EBinding為碳納米管與金屬原子的結合能,EMetal為沒有碳納米管的金屬表面能量,ECNT為沒有金屬表面的碳納米管能量.

為了研究多壁碳納米管的電子輸運性質,選取不同直徑、手性的單壁碳納米管(6,6),(11,0),(11,11)以及相同直徑、不同片層的多壁碳納米管.計算碳納米管電子輸運性質的模型是由碳納米管原胞經幾何優化后沿傳輸方向周期性拓展10個單位而構成的超胞體,如圖1所示,左右各選取2個周期作為半無限長電極,選取8個周期作為中心散射區.

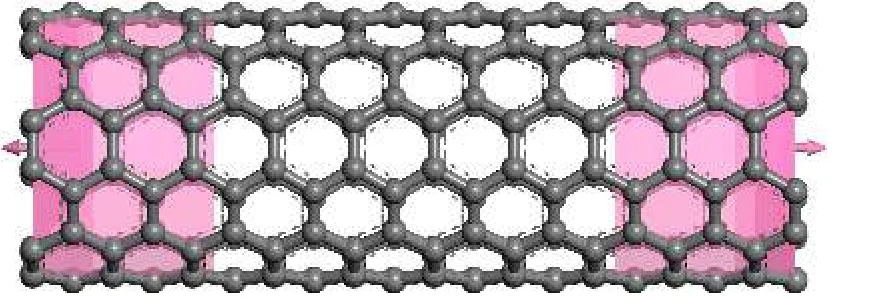
圖1 碳納米管電子輸運性質計算模型Fig.1.Calculation model for the electron transport properties of CNT.

本文基于DFTB計算電子結構,第一性原理結合非平衡格林函數(NEGF)[29,30]計算電子透射譜、電流-電壓曲線.密度泛函方法(DFT)可以比較精確地描述幾百個原子的幾何和電子特性,但是對于更大原子數、更為復雜的體系,密度泛函方法的研究受到很大的限制,而DFTB融合了DFT的精確性和緊束縛方法(TB)的高效性.DFTB具體的計算方法及參數設置如表1所列.

表1 DFTB的計算方法及參數設置Table 1.Scheme and parameter setting up in calculations with DFTB.

通過碳納米管的電流可以根據Landauer-Buttiker公式[31]進行計算:

其中,T(E,VB)是電壓在VB時電子能量為E的電子從左電極流向右電極的透射系數,可以由推遲和超前格林函數及線寬函數求得;f(E?μL) 和f(E?μR)分別為左、右電極的費米-狄拉克分布函數;μL和μR分別為左、右電極的化學勢,外部偏壓VBμL?μR,能量積分區域為 [μL,μR] .

3 結果與討論

3.1 碳納米管與金屬界面接觸的分子動力學模擬

碳納米管的尺寸較小,需要借助集成在掃描電子顯微鏡(SEM)里的微納操作機進行拾取、轉移、放置等操作來組裝納米電子器件.如圖2(a)和圖2(b)所示,當碳納米管與表面鍍金的原子力顯微鏡探針(AFM)的距離足夠近,在SEM下發生位移突變時可以判斷出碳納米管與AFM發生接觸.

圖2(c)和圖2(d)給出碳納米管與金界面接觸前的側視圖和主視圖模型,考慮到碳納米管與金界面接觸行為的產生主要是由于范德瓦耳斯力的作用,建立了端部開口不加氫的碳納米管模型,避免了模擬過程中氫鍵能與靜電能的影響,與宏觀實驗相符合.碳納米管與金界面接觸穩定后的狀態如圖2(e)和圖2(f)所示,碳納米管靠近金界面并且在徑向上有壓縮形變.

圖2 多壁碳納米管及其分子動力學模型 碳納米管和AFM (a)接觸前和 (b)接觸后的SEM圖像;原子模型的(c)側視圖和(d)主視圖;徑向壓縮形變后原子模型的(e)側視圖和(f)主視圖Fig.2.Picked CNT and its molecular dynamic model:SEM images of CNT and AFM (a) before contact,(b) after contact;(c) side view and (d) front view of model;after collapse (e) side view and (f) front view of model.

為了系統地解釋碳納米管與金屬界面接觸后的徑向壓縮形變程度與碳納米管的直徑、片層、接觸長度、金屬材料的性質等因素之間的關系,建立了不同直徑、長度的單壁碳納米管(6,6)和(11,11),不同片層的多壁碳納米管(6,6) @ (11,11)和(2,2)@ (6,6) @ (11,11)與金屬金、鋁、鉑的模型,如圖3所示.并對上述模型進行了分子動力學模擬,得到的范德瓦耳斯能差、結合能以及徑向壓縮形變的大小如表2所列.

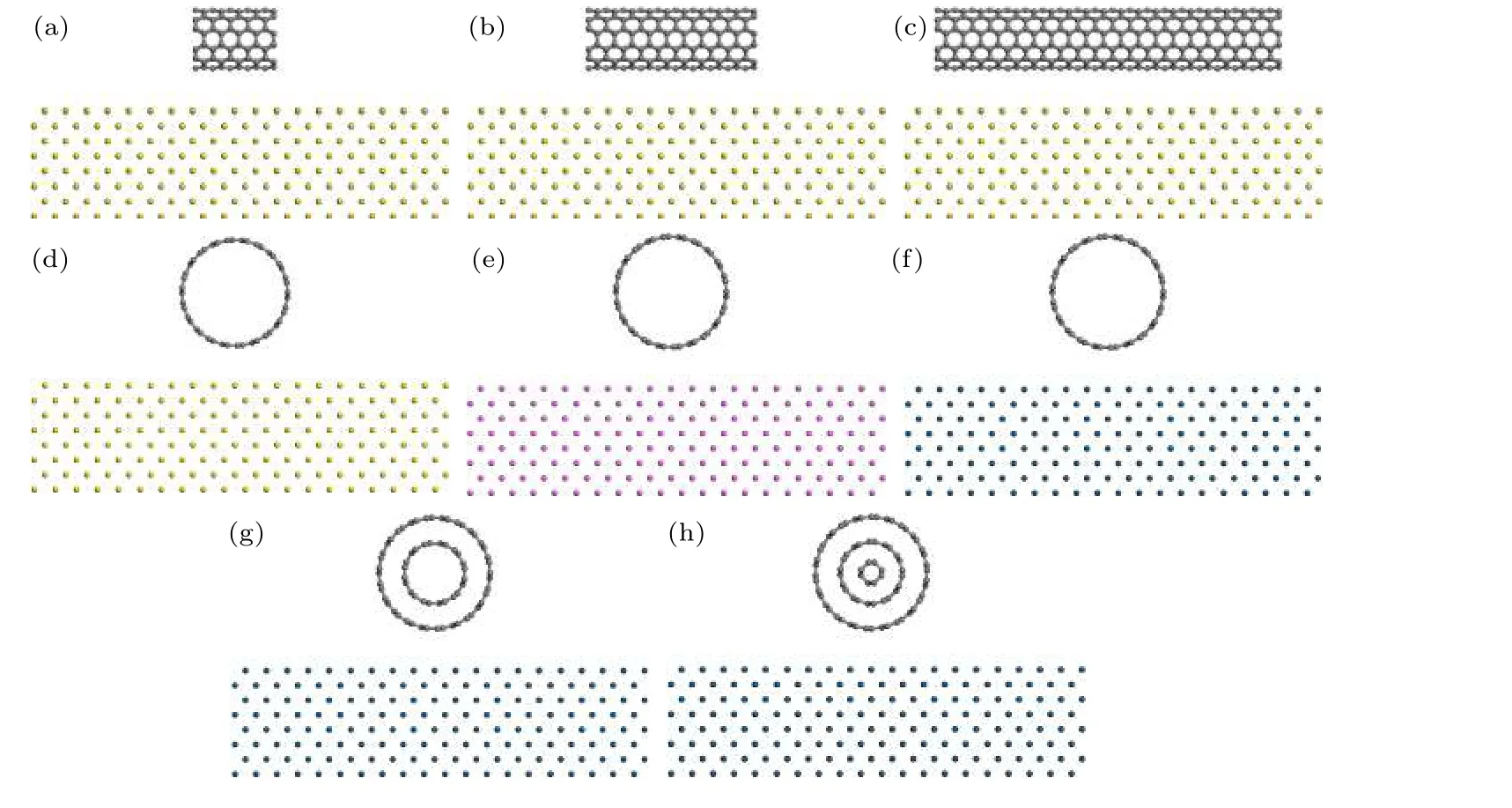
圖3 碳納米管與金屬表面接觸模型.接觸長度為 (a) 11.095 ?,(b) 23.422 ?,(c) 48.078 ?的扶手椅型碳納米管(6,6)與金;扶手椅型碳納米管(11,11)與(d)金、(e)鋁、(f)鉑;(g)雙壁碳納米管與鉑;(h)三壁碳納米管與鉑Fig.3.Contact behavior of CNT on metal.Armchir CNT(6,6) on gold with contact length of (a) 11.095 ?,(b) 23.422 ?,(c) 48.078 ?.Armchir CNT(11,11) contact behavior on (d) gold,(e) aluminium,(f) platinum.(g) DWCNT contact behavior on platinum.(h) MWCNT contact behavior on platinum.

碳納米管在受到范德瓦耳斯力的牽引作用逐漸靠近金屬表面并形成穩定狀態時會產生徑向壓縮形變并出現輕微的旋轉及軸向位移,設εr表示碳納米管的徑向壓縮形變量,定義εr為初始直徑和最終直徑之差與初始直徑的比值.本文使用范德瓦耳斯能差值以及結合能來表征碳納米管與金屬表面的黏著強度,結合能的負值表示碳納米管與金屬表面存在吸附作用.如圖4(a),(c)及表2所示,當單壁碳納米管(6,6)以11.095,23.422和48.078 ?的長度分別與金表面接觸形成穩定狀態后,碳納米管徑向壓縮形變量εr分別為0.1220,0.1074和0.0988,εr與碳納米管的長度成反比,即直徑相同的單壁碳納米管的管長越長,εr越小,同時原子數的增多導致范德瓦耳斯能差與結合能增大,使得碳納米管與金屬界面的黏著強度增加.當單壁碳納米管(11,11)以相同長度23.410 ?分別與金、鋁、鉑金屬表面接觸形成穩定狀態后,由于金屬材料性質的不同,碳納米管與鉑表面接觸引起的范德瓦耳斯能差及結合能最大,得到的黏著強度也就最大,穩定狀態下的εr為0.2494;碳納米管與鋁表面接觸引起的范德瓦耳斯能差及結合能最小,得到的黏著強度也就最小,εr為0.1583.通過分子動力學模擬后得到單壁碳納米管(6,6)和(11,11)與金表面接觸后的εr分別為0.1074和0.1984,單壁碳納米管的直徑越大,范德瓦耳斯能差以及結合能增加,黏著強度相應增大,εr也越大.當直徑、長度相同的碳納米管以單壁、雙壁、三壁的形式與鉑表面接觸后得到的εr分別為0.2494,0.0967和0.0717,碳納米管的管壁越多,εr就越小,但是管壁的增多并沒有引起范德瓦耳斯能差的變化,這是由于管壁之間互相存在排斥和吸引作用,碳納米管的層間相互作用抵消了一部分碳納米管與金屬表面接觸后引起的范德瓦耳斯能,而結合能的大小由于原子數的增多而上升,黏著強度增加.

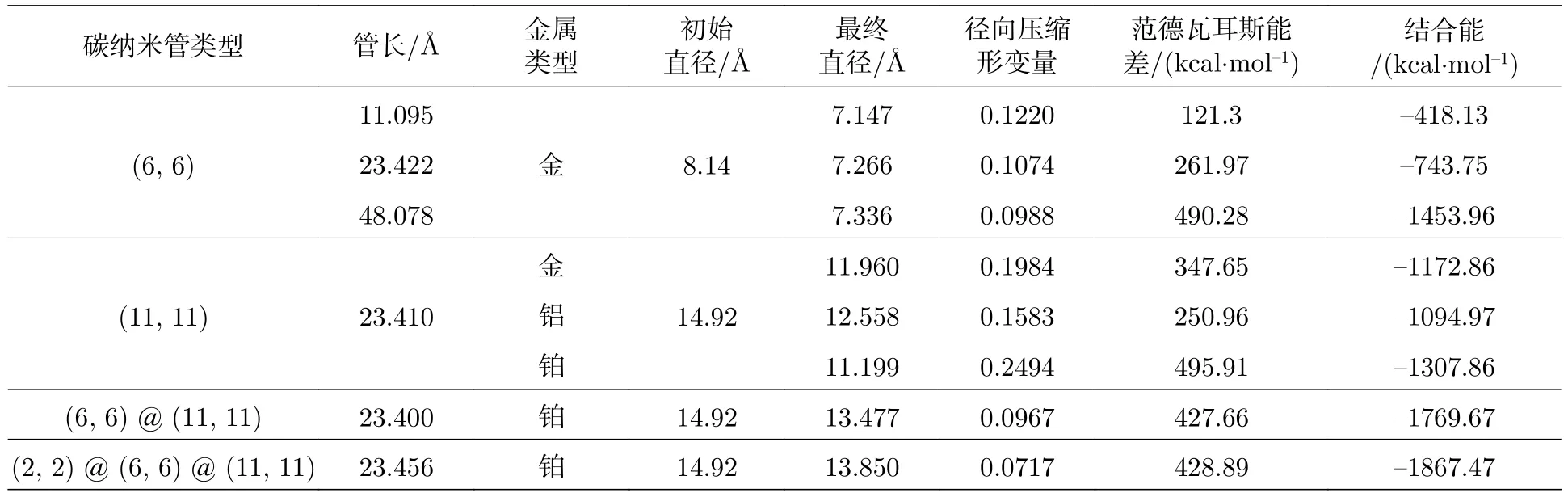
表2 碳納米管與金屬界面接觸的分子動力學模擬Table 2.Molecular dynamic of different CNT on different metal.

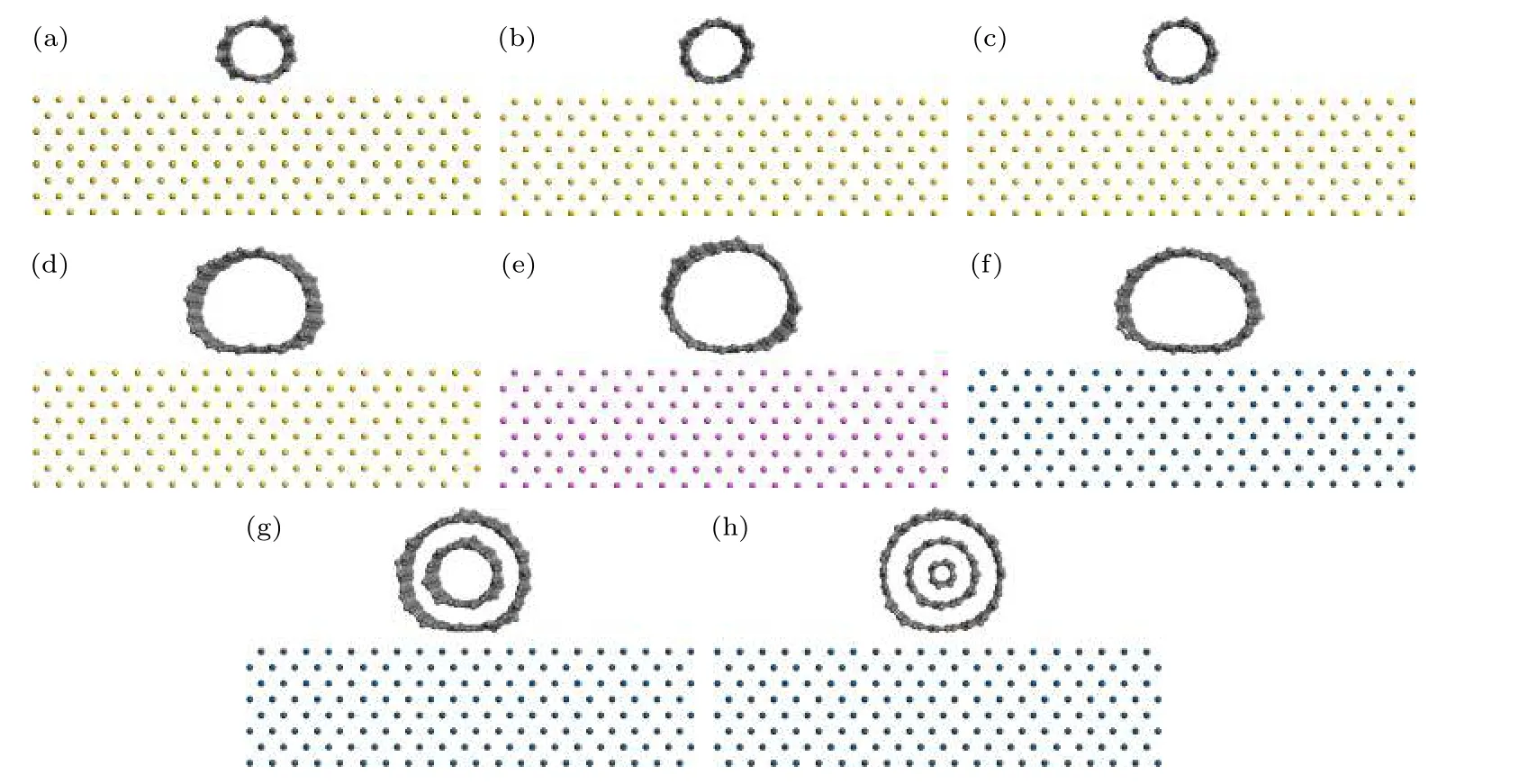
圖4 碳納米管徑向壓縮形變后原子模型主視圖接觸長度為(a) 11.095 ?,(b) 23.422 ?,(c) 48.078 ?的扶手椅型碳納米管(6,6)與金;扶手椅型碳納米管(11,11)與(d)金、(e)鋁、(f)鉑;(g)雙壁碳納米管與鉑;(h)三壁碳納米管與鉑Fig.4.Front view after collapse of CNT.Armchir CNT(6,6) on gold with contact length of (a) 11.095 ?,(b) 23.422 ?,(c) 48.078 ?.Armchir CNT (11,11) contact behavior on (d) gold,(e) aluminium,(f) platinum.(g) DWCNT contact behavior on platinum.(h) MWCNT contact behavior on platinum.

上述分析表明:碳納米管的直徑大小、片層數量、碳納米管與金屬的接觸長度以及金屬材質對碳納米管的徑向壓縮形變具有不可忽視的影響.當使用碳納米管進行電子器件的組裝時,應當選取直徑較小的多壁碳納米管作為操作對象,并選用與碳納米管接觸時能夠形成較大范德瓦耳斯能差以及結合能的金屬材質(例如鉑)作為源漏極,同時在操作過程中增加碳納米管與金屬之間的接觸長度,這些既能保證碳納米管和金屬之間存在較大的黏著力,也能減少碳納米管的徑向壓縮形變量,以維持碳納米管本身的電子輸運特性.

3.2 碳納米管電子輸運性質

為了系統地解釋碳納米管徑向壓縮形變對其電子輸運特性的影響,首先研究徑向壓縮形變量εr對直徑不同的扶手椅型單壁碳納米管電子輸運性質的影響,分別選取直徑為8.14和14.92 ?的扶手椅型碳納米管(6,6)和(11,11)作為研究對象,并依次選用0,0.10和0.15的徑向壓縮形變量εr進行模擬.圖5(a)和圖5(b)分別給出在[–2 V,+2 V]的偏壓范圍下扶手椅型碳納米管(6,6)和(11,11)在不同εr下的電流-電壓曲線.由圖5可知,扶手椅型碳納米管在不同εr的情況下,其隧穿電流均關于(0,0)點對稱,電流在[–1.3 V,+1.3 V]較小的偏壓范圍內呈線性變化;扶手椅型碳納米管(6,6)和(11,11)的直徑并不相同,但在無εr時,最大正負偏壓下電流的最值均在300 μA附近.隨著正負偏壓的絕對值的增大,電流-電壓曲線由線性狀態向非線性狀態轉變,并且εr越大,非線性特征越明顯.當εr為0.15時,扶手椅型碳納米管(6,6)的電流在[–2.0 V,–1.6 V]和[1.6 V,2.0 V]偏壓范圍內的增量非常小,甚至有些降低,說明電子導電通道并沒有隨著偏壓的增加而增加,存在電子電導平臺效應.這是由于徑向壓縮形變使得碳納米管的直徑變小,在相對較高的偏壓下電子動能增大,電子間散射增強,導致了電流隨偏壓的增大不再線性增加.研究結果表明,扶手椅型碳納米管受到的徑向壓縮形變越大,碳納米管電流-電壓曲線非線性特征越明顯;碳納米管的直徑越大,徑向壓縮形變對其電子輸運能力的影響越小.

為了進一步分析圖5中電流-電壓曲線的變化規律,圖6(a)—圖6(c)分別給出εr為0,0.10以及0.15時扶手椅型碳納米管(6,6)在0,0.5,1.0,1.5及2.0 V偏壓下的透射譜,圖7給出εr為0時扶手椅型碳納米管(11,11)在0,0.5,1.0,1.5及2.0 V偏壓下的透射譜,取費米能級E=0 eV為能量參考點,偏壓窗為[–VB/2,VB/2],即圖6和圖7中黑色虛線之間的區域,對通過偏壓窗的透射系數進行積分可以得到碳納米管的電流大小.

圖6 扶手椅型碳納米管(6,6)在0,0.5,1.0,1.5及2.0 V偏壓下的透射譜 (a) εr=0 ;(b) εr=0.10 ;(c)εr=0.15Fig.6.Transmission spectrum of Armchair CNT (6,6) under the bias voltage of 0,0.5,1.0,1.5 and 2.0 V with different radial deformation:(a) εr=0 ;(b) εr=0.10 ;(c) εr=0.15 .

如圖6和圖7所示,零偏壓時費米能級處的透射系數均為2,且透射系數不隨偏壓的增大而產生變化,這表明扶手椅型碳納米管(6,6)及(11,11)是金屬性的,驗證了電流在[–1.3 V,+1.3 V]低偏壓范圍內呈線性變化的規律.當εr為0且偏壓窗大小相同時,圖6(a)以及圖7中積分面積的大小幾乎相同,說明直徑不同的扶手椅型碳納米管(6,6)和(11,11)在相同偏壓情況下電子導通通道的數量幾乎相同,使得電流的大小也幾乎相同,驗證了圖5(a)和圖5(b)中兩條黑色方塊的電流-電壓曲線幾乎相同的規律.隨著偏壓的增加,圖6中費米能級處的透射平臺數值始終保持為2,但透射平臺的寬度逐漸減小,遠離費米能級的透射平臺的高度逐漸降低,并向費米能級移動.特別地,碳納米管的εr越大,遠離費米能級的透射平臺下降得越快,向費米能級移動得也越快.上述現象導致遠離費米能級的透射平臺的數值下降為1,并隨著偏壓的增加而進入偏壓窗.在εr為0.10且有較大偏壓時,積分面積的增量減少;在εr為0.15且有較大偏壓時,積分面積幾乎停滯不變,這個結果驗證了圖5中電流隨偏壓非線性變化的規律.

圖7 εr=0 時扶手椅型碳納米管(11,11)在0,0.5,1.0,1.5及2.0 V偏壓下的透射譜Fig.7.Transmission spectrum of Armchair CNT (6,6) with the radial deformation of 0 under the bias voltage of 0,0.5,1.0,1.5 and 2.0 V.

為了研究不同εr對手性不同的單壁碳納米管電子輸運性質的影響,選取直徑為8.61 ?的鋸齒型碳納米管(11,0)在εr分別取0,0.10及0.15時的電流-電壓特性進行分析,結果如圖8所示.可以看出,電流-電壓曲線均關于(0,0)點對稱.眾所周知,碳納米管(m,n)的金屬性或半導體性與m,n的值有關,當m=3n時,碳納米管呈金屬性,其他情況時則呈半導體特性,所以鋸齒型碳納米管(11,0)屬于半導體性碳納米管.圖8黑色方塊曲線為在εr=0 時得到的電流-電壓曲線,符合半導體材料電流-電壓曲線的特性,即需要一定的電壓才能導通,且導通后隨著偏壓的增加,電流迅速地非線性增長.當εr0 時,電流在[–1 V,1 V]偏壓范圍內幾乎為零,呈現截止狀態,在較大偏壓范圍下呈非線性增長;當εr0.10和εr0.15 時,電流在[–0.4 V,0.4 V]和[–0.1 V,0.1 V]小偏壓范圍內幾乎為零,在[–2 V,–0.4 V],[0.4 V,2 V]和[–2 V,–0.1 V],[0.1 V,2 V]偏壓范圍內隨偏壓絕對值的增加,電流的絕對值呈線性增長趨勢.特別地,在[–2 V,+2 V]范圍內,電流絕對值的最值也在300 μA附近,結合圖5可以看出,在相同的偏壓狀態下,電流最值的大小與管徑無關,同時存在一定徑向壓縮形變的半導體性碳納米管也可以達到金屬性碳納米管的電流最值.

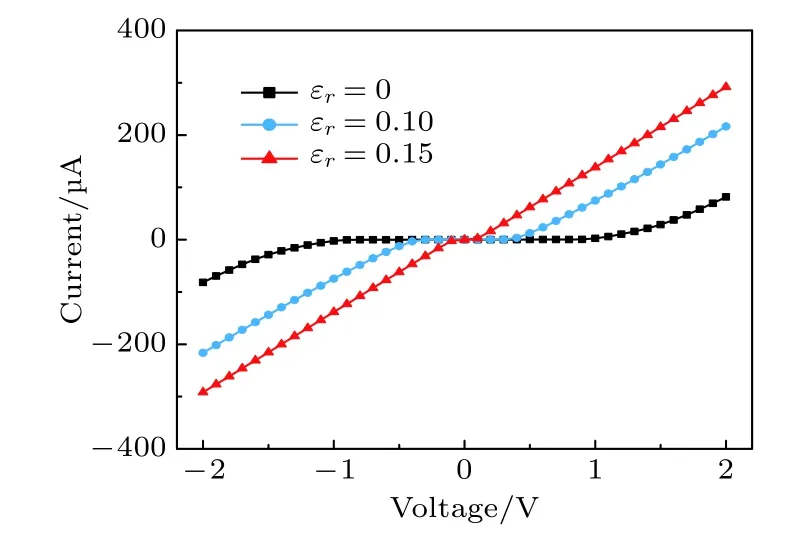
圖8 鋸齒型碳納米管(11,0)在 εr 為0,0.1和0.15下的電流-電壓(I-V)曲線Fig.8.Current-voltage (I-V) curve of Zigzag CNT (11,0)with the radial deformation of 0,0.1 and 0.15.

為進一步解釋圖8中電流變化規律,圖9(a)—圖9(c)給出εr為0,0.1及0.15時鋸齒型碳納米管(11,0)在0,0.2,0.5,1及1.5 V偏壓下的透射譜,其中黑色虛線代表偏壓窗,灰色陰影部分代表偏壓窗內透射系數的積分面積.

如圖9所示,在費米能級右邊存在一個數值為零的透射平臺,透射平臺的寬度隨著徑向壓縮形變量的增加而減小;相反地,費米能級兩側數值為2的透射平臺的寬度隨徑向壓縮形變量的增加而增加.隨著偏壓的增加,費米能級兩側不為零的透射平臺的高度逐漸降低,且徑向壓縮形變量越大,透射平臺下降得越快,這與扶手椅型碳納米管(6,6)透射譜的變化規律相似;但不同的是,費米能級兩側不為零的透射平臺隨著偏壓的增加逐漸遠離費米能級,且徑向壓縮形變量越大,透射平臺遠離費米能級越快.在εr為0.1和0.15時,隨著鋸齒型碳納米管(11,0)兩側偏壓慢慢增加,在費米能級處出現了新的數值為2的透射平臺,并且透射平臺的寬度隨著偏壓的增加而增加,使得積分面積不斷增加.上述結果驗證了圖8中在較大偏壓下且εr為0.1和0.15時,電流呈線性增長的規律.

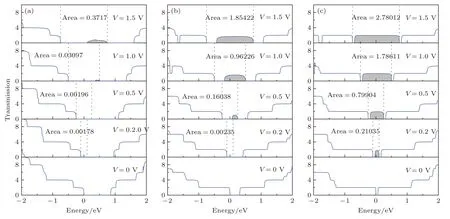
圖9 鋸齒型碳納米管(11,0)在0,0.2,0.5,1及1.5 V偏壓下的透射譜 (a) εr=0 ;(b) εr=0.1 ;(c)εr=0.15Fig.9.Transmission spectrum of Zigzag CNT (11,0) under the bias voltage of 0,0.2,0.5,1 and 1.5 V with different radial deformation:(a) εr=0 ;(b) εr=0.1 ;(c) εr=0.15 .

在不同徑向壓縮形變下,扶手椅型碳納米管與鋸齒型碳納米管的電子輸運性質的變化規律是不同的,下面通過分析碳納米管的電子結構來解釋這一現象.使用本文計算參數模擬得到:當εr為0,0.1以及0.15時,扶手椅型碳納米管(6,6)的能隙分別為0.028,0.132和0.341 eV,即εr越大,能隙越大;當εr為0,0.1以及0.15時,鋸齒型碳納米管(11,0)的能隙分別為0.857,0.307和0.020 eV,即εr越大,能隙越小.對于扶手椅型碳納米管來說,不存在徑向壓縮形變時的能隙應嚴格為零,但因為本文是使用第一性原理進行理論計算的,這是一種近似計算方法,所以計算結果0.028 eV與實際會有一定的誤差.扶手椅型碳納米管具有很高的軸向對稱性,徑向壓縮形變破壞了扶手椅型碳納米管的結構對稱性,產生量子排斥效應,導致能隙變大.鋸齒型碳納米管的對稱性較低,徑向壓縮形變降低了鋸齒型碳納米管的電子的束縛度,使得原簡并能級發生分裂,導致能隙變小.能隙的增大使得扶手椅型碳納米管的電流-電壓曲線產生了非線性的變化;能隙的降低使得鋸齒型碳納米管從原來的半導體性向金屬性轉變,電流-電壓曲線由非線性向近似線性轉變.

為了研究不同εr對片層不同的碳納米管電子輸運性質的影響,選取直徑為14.92 ?的雙壁碳納米管(6,6)@(11,11)和三壁碳納米管(2,2)@(6,6)@(11,11),圖10(a)和圖10(b)分別為雙壁碳納米管和三壁碳納米管在εr取0,0.1及0.15時的電流-電壓曲線.雙壁碳納米管和扶手椅型單壁碳納米管(6,6)及(11,11)的電流-電壓曲線變化規律相同,但片層的增加,電子數與電子輸運通道也相應地增加了,所以在相同偏壓下,雙壁碳納米管電流絕對值的最值在600 μA附近,三壁碳納米管電流絕對值的最值在800 μA附近.上述現象表明,碳納米管管壁的層數越多,電子輸運能力就越強,在相同偏壓下得到的電流也越大.如圖10(b)所示,三壁碳納米管的伏安特性曲線出現了不對稱性,在正負偏壓絕對值相等的情況下,負偏壓下電流的絕對值大于正偏壓下的電流,同樣地,負偏壓下隨徑向壓縮形變量增加,電流的非線性變化特征也越顯著.這是由于三壁碳納米管存在層間耦合使得能級簡并度降低,體系的增大使得費米能級附近電子態增多,電子能夠通過相鄰管間快速振動產生躍遷,導致了電流出現較大振蕩以及電流-電壓曲線不關于原點對稱.

為進一步解釋圖10中電流變化規律,圖11(a)給出εr為0時,雙壁碳納米管在0,0.5,1.0,1.5及2.0 V偏壓下的透射譜;圖11(b)給出εr為0時,三壁碳納米管在–1.5,–0.5,0,0.5及1.5 V偏壓下的透射譜,其中黑色虛線代表偏壓窗,灰色陰影部分代表偏壓窗內透射系數的積分面積.

圖10 碳納米管在 εr 為0,0.1和0.15下的電流-電壓曲線 (a)雙壁;(b)三壁Fig.10.Current-voltage curve of CNT with the radial deformation of 0,0.1,0.15:(a) DWCNT;(b) MWCNT.

圖11 εr=0 時碳納米管的透射譜 (a)雙壁碳納米管在0,0.5,1.0,1.5及2.0 V偏壓下的透射譜;(b)三壁碳納米管在–1.5,–0.5,0,0.5及1.5 V偏壓下的透射譜Fig.11.Transmission spectrum of CNT with the radial deformation of εr=0 :(a) DWCNT under the bias voltage of 0,0.5,1.0,1.5 and 2.0 V;(b) MWCNT under the bias voltage of–1.5,–0.5,0,0.5 and 1.5 V.

如圖11(a)所示,費米能級處的透射系數在零偏壓時為4,且不隨偏壓的增大而產生變化,這表明雙壁碳納米管(6,6) @ (11,11)是金屬性的,驗證了圖10(a)中電流在低偏壓范圍內呈線性變化的規律.當εr0 且偏壓窗大小相同時,雙壁碳納米管(6,6) @ (11,11)的積分面積近乎是扶手椅型單壁碳納米管(6,6)和(11,11)的2倍,這是由于管壁的增加導致了電子導通通道的數量成倍增加,使得電流大小也成倍地增加,驗證了圖10(a)中黑色方塊電流-電壓曲線的斜率是圖5中黑色方塊電流-電壓曲線的2倍.雙壁碳納米管透射譜的變化規律與扶手椅型單壁碳納米管的變化規律相似,即隨著偏壓的增加,費米能級處的透射平臺數值始終保持為4,透射平臺的寬度減小,遠離費米能級的透射平臺高度降低并向費米能級移動.如圖11(b)所示,三壁碳納米管體系增大,電子數增加,電子導通通道數量增加,導致了在相同偏壓窗下三壁碳納米管的積分面積比單壁碳納米管和雙壁碳納米管的大.同時,隨著碳納米管片層數量的增多,三壁碳納米管存在層間耦合作用,使得能級分裂,三壁碳納米管的透射譜存在多個透射峰且波動較大.隨著偏壓的增加,遠離費米能級處的透射系數下降并進入到偏壓窗口中,特別地,遠離費米能級處的透射系數在負偏壓下下降的速度比在正偏壓下的慢,使得在偏壓窗大小相同時,負偏壓下的積分面積大于正偏壓下的積分面積,驗證了圖10(b)中三壁碳納米管的電流-電壓曲線是關于原點不對稱的.

4 結論

利用分子動力學方法研究了碳納米管與不同金屬界面的接觸行為,結果表明:徑向壓縮形變量εr與碳納米管的長度、直徑、片層數量成反比,同時由于金屬材料性質的不同,碳納米管與鉑表面接觸后得到的εr比金、鋁表面的大.基于緊束縛密度泛函理論和非平衡格林函數結合的第一性原理,系統地研究了不同直徑、手性、片層、徑向壓縮形變碳納米管的電子輸運性質.結果表明:當不存在徑向壓縮形變時,金屬性單壁碳納米管的電流在[–2 V,2 V]的偏壓范圍內呈線性增長趨勢,電流的最值在300 μA附近,電流大小與直徑大小無關;當金屬性單壁碳納米管受到徑向壓縮形變時,電流-電壓曲線在相對較大的偏壓下會呈現非線性增長趨勢.半導體性單壁碳納米管受到徑向壓縮形變后,電流-電壓曲線會向金屬性轉變.在同等偏壓下,雙壁碳納米管的電流比單壁碳納米管的高1倍;在受到徑向壓縮形變時,雙壁碳納米管電流-電壓曲線產生的變化與金屬性單壁碳納米管的電流-電壓曲線變化規律一致.在同等偏壓下,三壁碳納米管的電流比單壁碳納米管的高2倍,其電流-電壓曲線存在較大振蕩.上述研究結果可為設計制造基于碳納米管的納米電子器件和微納集成電路提供理論依據.

感謝上海大學高性能計算中心提供的計算資源和技術支持.