高壓下Py-FeO2、Py-FeOOH 和ε-FeOOH 晶體結構與彈性特征的第一性原理研究

顧小雨，劉 雷

（中國地震局地震預測研究所高壓物理與地震科技聯合實驗室，北京 100089）

地球表面70%被水覆蓋，同時更大量的水以不同形式賦存在地球內部。地表的水可以通過板塊俯沖作用被帶到地球內部，隨著深度的增加，地球內部的水將經歷復雜的遷移過程[1]。水在地球深部中的運移和儲存會對地球內部動力學和物質循環演化產生影響，同時還影響地殼和水圈的演化規律。水的存在顯著影響成巖礦物的化學和物理性質，包括礦物相關系、熔化溫度、流變特性、電導率和地震速度等。在地幔深度范圍內，水主要以羥基形式存在于礦物晶格[2]。最近對含水礦物超石英（stishovite）的原位激光與X 射線衍射（X-ray diffraction，XRD）實驗表明，超石英可以在地幔溫度壓強條件下穩定存在，超石英有可能成為下地幔中運輸和儲存水的關鍵礦物[3]。Li 等[4]使用從頭算分子動力學和熱力學方法計算了20～135 GPa 和5 800～5 000 K 條件下鐵與硅酸鹽熔體之間的水的分配比，驗證了水的親鐵性，發現地核可能是一個包含地球大部分水的大型水庫，這可能是引起地心低密度的原因。但是，目前水如何輸送到地球的深部，以及在哪些階段進行，仍然存在很大的爭議。地幔物質的性質或許可以通過某些地震學觀測約束得到，但是理解地幔的具體組成需要完備的、高質量的高溫高壓礦物數據，如密度、穩定性、彈性性質[2-27]等。因此，研究高溫高壓下含水礦物的性質，對了解地球深部的結構、礦物組成以及深部水循環具有重要意義。

本研究選擇地球深部重要的含水相礦物黃鐵礦型FeO2（Py-FeO2）、FeOOH（Py-FeOOH）以及ε-FeOOH[5-7]作為研究對象。Py-FeO2和Py-FeOOH 是2016 年在高溫高壓實驗中被發現穩定存在的新礦物[5-6]，實驗和理論結果都證明了從ε-FeOOH 到黃鐵礦型FeOOH 的轉化關系，ε-FeOOH 和黃鐵礦型FeOOH 之間的相邊界位于60 GPa、1 500 K[7]。

Hu 等[5]使用第一性原理計算和實驗，首次確定了76 GPa、1 800 K 條件下穩定存在的P 相（黃鐵礦型FeO2）。Bo 等[8]利用密度泛函理論（density functional theory，DFT）和DFT + DMFT 方法研究了FeO2的電子結構和結構性質，FeO2的晶體結構由Fe2+和O22-二聚體組成，其中Fe 離子被八面體O 原子包圍，FeO2在高壓下表現出金屬-絕緣體（MIT）轉變（由氧二聚體鍵長度變化驅動的絕緣類型）。Hu 等[6]進一步確定了P 相至少穩定到133 GPa、2 000 K 條件下，實驗中還發現了具有黃鐵礦型結構的FeOOHx，利用第一性原理計算方法約束和量化了P 相（Py-FeOOHx）中的氫含量（0.39 ＜x＜ 0.81）。Nishi 等[7]發現了新黃鐵礦型FeOOH 相，可在地幔底部的條件下穩定存在，并最終分離成Fe2O3和H2O。Zhang 等[9]進行了第一性原理計算，評估了黃鐵礦型FeO2的穩定性和彈性性質。Huang 等[10]進行了第一性原理計算，發現氫的加入顯著影響了高壓下黃鐵礦型FeO2H-FeO2體系的結構特性、壓縮行為和各向異性。Liu 等[11]利用高壓實驗和理論計算分析了Py-FeOOHx的聲速結果，發現鐵和水能在86 GPa、2 200 K 條件下反應生成Py-FeOOHx。Yuan 等[12]基于原位XRD 實驗和第一性原理計算，研究了Fe-H2O 在高壓下的相變特征，發現在低于78 GPa 的條件下產生FeHx和FeO，高于78 GPa 的條件下生成Py-FeOOHx和FeHx。Zhuang 等[13]利用Kawai 型多砧壓機和XRD 實驗證明了在Py-FeOOHx轉化為ε-FeOOH 的過程中，ε-FeOOH 發生了部分脫氫反應，以ε-FeOOHx的形式存在于下地幔中。Deng 等[14]利用第一性原理分子動力學研究了P 相的固液兩相的熱彈性性質，發現通過相對少量的熔融FeOOHx可以解釋觀察到的地幔邊界上方超低速區（ultra-low velocity zones，ULVZs）的地震異常。Hou 等[15]結合高壓電導率實驗、拉曼光譜測量和第一性原理模擬，研究了黃鐵礦型FeOOHx（x≤ 1）中氫的狀態，發現當壓強超過73 GPa時，對稱的羥基鍵被軟化，H（或質子）在其晶體位置附近變得分散。高度擴散的氫為電荷和質量提供了新的輸運機制，這決定了地球深部的電導率和磁性等地球物理性質，以及地幔底部中氧化還原、氫循環和氫同位素混合的地球化學過程。Thompson 等[16]利用第一性原理計算了黃鐵礦體系FeOOHAlOOH 在60～140 GPa 條件下的彈性性質和地震波速，發現黃鐵礦型(Al0.5～0.6, Fe0.4～0.5)OOH 可以很好地吻合下地幔中超低速區的壓縮和剪切速度，富含鋁的CaCl2型(Al,Fe)OOH 可能形成大的低剪切速度區域（large low shear-wave velocity provinces，LLSVPs）。

Bendeliani 等[17]在9.0 GPa、400 K 條件下合成了ε-FeOOH，XRD 和中子衍射實驗[18-20]表明，ε-FeOOH 具有空間群Pmn21的正交結構。實驗發現[21-22]，α-FeOOH 在5 GPa、200 ℃的條件下需要較長的反應時間才能生成ε-FeOOH。Suzuki[23-24]利用同步加速XRD 實驗，得到了8.6 和11 GPa、700 K 溫壓條件下ε-FeOOH 的晶體結構參數和體積模量（K）。Otte 等[25]利用DFT 確定了ε-FeOOH 的穩定性，同時得到了ε-FeOOH 的結構、磁性和電子性。Gleason 等[26]采用實驗與DFT 計算相結合的方法，研究了ε-FeOOH 的結構和電子自旋躍遷。Thompson 等[27-28]使用DFT 研究了ε-FeOOH 的結構和彈性性質，并利用XRD 實驗對ε-FeOOH 的高壓行為進行研究，發現在0～75 GPa 壓力范圍內ε-FeOOH 有2 個連續的結構相變，(18 ± 1) GPa 時由于壓力誘導的氫鍵對稱化而產生的P21nm→Pnnm結構變化，在(45 ± 2) GPa時經歷了等結構的一級相變。

Py-FeO2、Py-FeOOH 和ε-FeOOH 3 種礦物作為Fe-H2O 體系尚未被系統地研究，Py-FeOOH 和Py-FeO2的彈性性質還有待進一步探索。第一性原理方法在探索物質在高溫高壓下的結構、彈性、譜學等方面取得了豐碩的成果，且計算精度不斷提高[29-39]。為此，本研究通過第一性原理計算分析0～350 GPa 范圍內的Py-FeO2和Py-FeOOH 以及0～170 GPa 范圍內的ε-FeOOH 的晶體結構、彈性模量以及波速等性質，系統地比較3 種礦物的物性差異，為了解高壓下Fe-H2O 體系礦物物性演化及其在地球深部賦存特征提供數據支持。

1 方法與理論

采用基于DFT 的第一性原理方法，使用Materials Studio-CASTEP[40]模塊，計算了Py-FeO2、Py-FeOOH 和ε-FeOOH 在不同壓強下的結構變化。晶胞結構優化計算使用基于PBE（Perdew-Burke-Ernzerh）交換關聯函數的廣義梯度近似方法（generalized gradient approximation，GGA），GGA 方法更適用于模擬含氫鍵體系礦物[24,27,35]。在收斂性測試的基礎上，平面波基組展開的截斷能均為571.4 eV，布里淵區設置K點的網格參數為6 × 6 × 6（Py-FeO2）、6 × 6 × 6（Py-FeOOH）、5 × 6 × 8（ε-FeOOH）。

第一性原理計算的第一步需要對Py-FeO2、Py-FeOOH 和ε-FeOOH 的晶體模型進行幾何優化，求得局域最穩定結構，晶體結構模型如圖1 所示。Py-FeO2和Py-FeOOH 屬于立方晶系（空間群Pa3，原子序數Z= 4）[5-7]，ε-FeOOH 為正交晶系（空間群Pmn21，Z= 2），結構中的Fe 和O 原子形成了CaCl2型結構[25]。不同壓強下ε-FeOOH、Py-FeOOH 和Py-FeO2的晶胞參數及結構內各原子位置都通過BFGS 方法進行了優化。通過應力-應變關系計算彈性常數，控制應變大小為0.05，以保障ε-FeOOH、Py-FeOOH 和Py-FeO2處于彈性形變狀態。彈性模量利用Voigt-Reuss-Hill 近似方法計算得出。

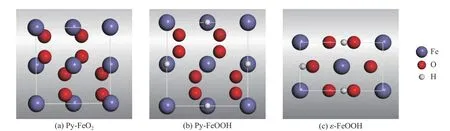
圖1 Py-FeO2、Py-FeOOH 和ε-FeOOH 的晶體結構Fig. 1 Crystal structure of Py-FeO2, Py-FeOOH and ε-FeOOH

2 結果與討論

首先對Py-FeO2、Py-FeOOH 和ε-FeOOH 的晶體結構進行優化，得到穩定結構的晶格參數，見表1。Py-FeO2的晶格常數和晶胞體積與前人計算值[5]的相對偏差分別為0.14%和0.40%，與實驗值[5]的相對偏差分別為2.4%和1.7%。Py-FeOOH 的晶胞體積與前人計算值[7]的相對偏差為2.3%，晶格常數和晶胞體積與實驗值[5,7]的相對偏差都不超過0.5%。ε-FeOOH 的晶胞體積與前人計算值[25]的相對偏差為0.02%，晶胞體積與實驗值[17,23-24]的最大相對偏差為14%，晶格常數a、b、c與實驗值[17,23-24]的最大相對偏差分別為4.8%、4.7%、3.4%，前人研究結果中，ε-FeOOH 的體積模量計算值[24]與實驗值[17,23-24]的最大相對偏差為32%。ε-FeOOH 的晶格常數、晶胞體積和體積模量與實驗值的偏差略大，主要是由于計算中使用了GGA 方法，從而低估了結構內原子間的內聚力[17,23-24,41-43]。總體而言，本研究的計算結果與文獻中的計算和實驗結果[5-7,17,23-25]的一致性較好，表明采用的計算方法和參數設置是合理可靠的。

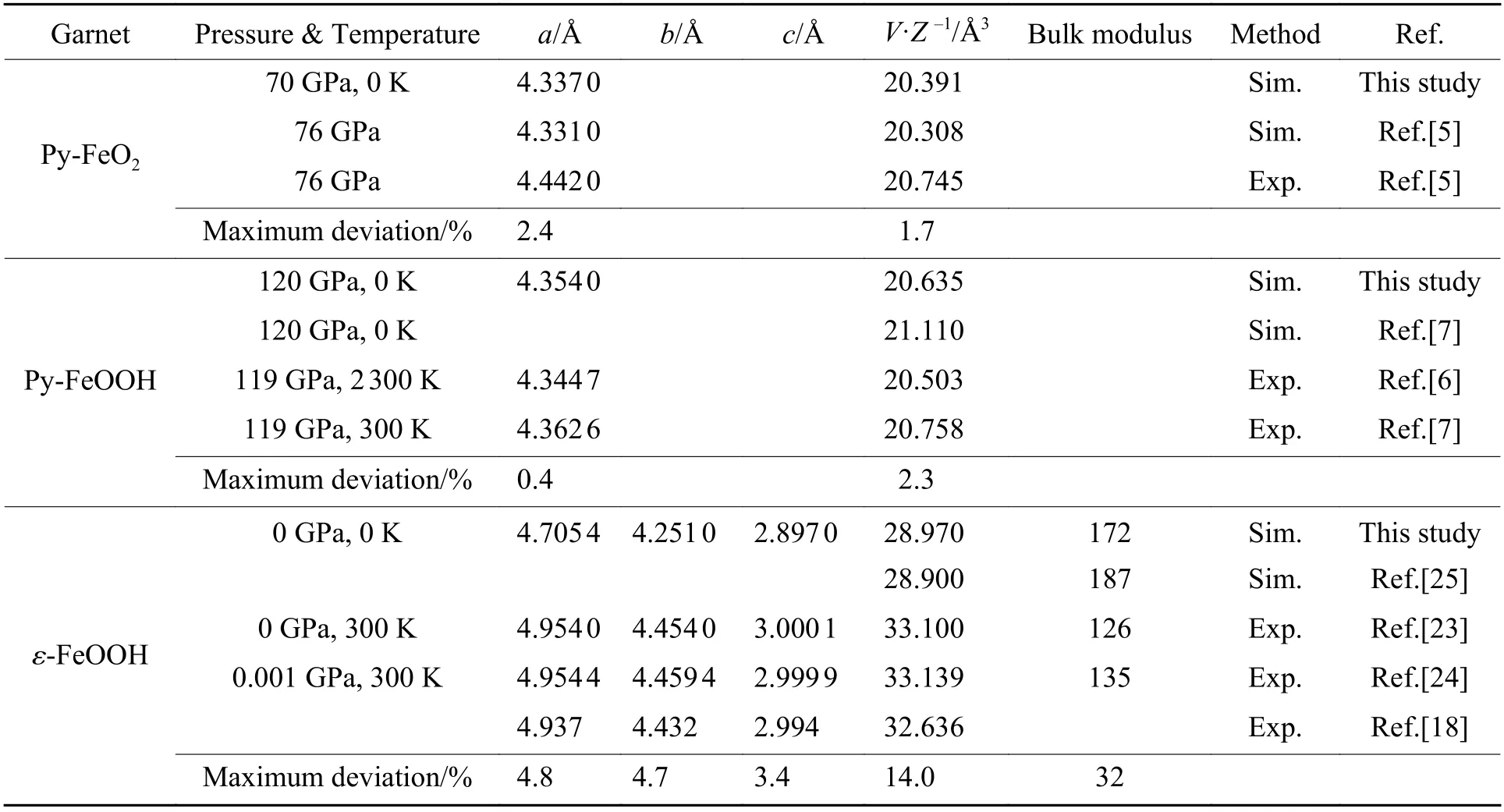
表1 Py-FeO2、Py-FeOOH 和ε-FeOOH 的晶格參數和體積模量Table 1 Lattice parameters and bulk moduli of Py-FeO2, Py-FeOOH and ε-FeOOH

2.1 晶體結構和密度變化

0～350 GPa 條件下的Py-FeO2和Py-FeOOH 以及0～170 GPa 條件下的ε-FeOOH 的晶格常數如圖2 所示。Py-FeO2和Py-FeOOH 的結構為立方晶系（a=b=c），晶格常數隨壓強的增加呈逐漸減小的趨勢，晶胞體積也隨著壓強的增加而降低。ε-FeOOH 的結構為正交晶系（a、b、c不相等），晶格常數隨著壓強的增大而逐漸減小，0～170 GPa區間內c軸長度相比a、b軸長度大幅減小，但在33 GPa 附近有異常突變，a、b軸長度突然增加，c軸長度突然減小。c軸上只有共邊的氧原子和氫鍵，相比有共邊的鐵原子以及鐵氧鍵的a、b軸，更容易被壓縮。本研究在確定計算方法和參數后，具體計算了0～350 GPa 壓力條件下Py-FeO2、Py-FeOOH 以及0～170 GPa 壓力條件下ε-FeOOH的晶格常數和密度。

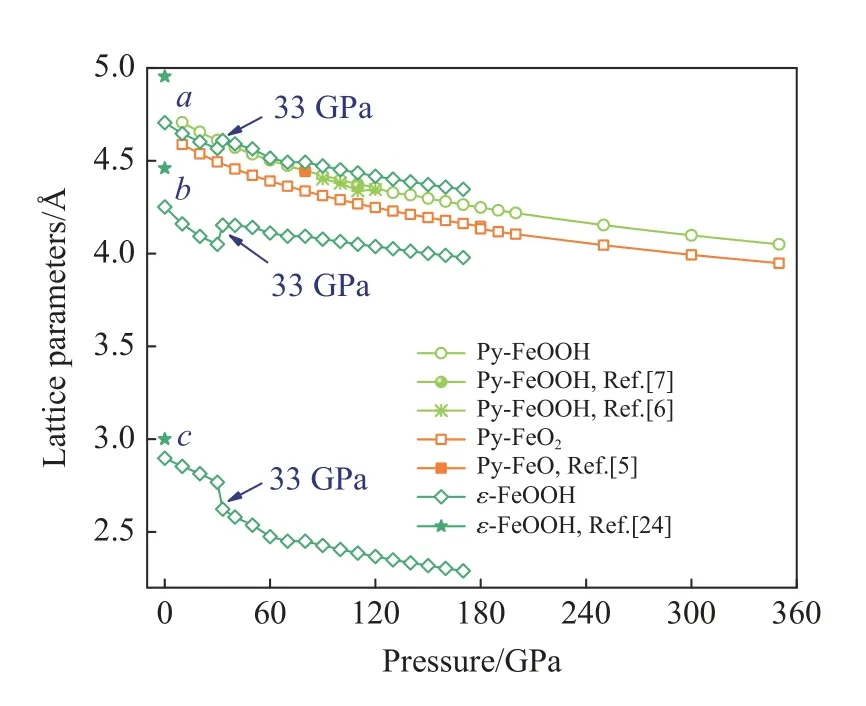
圖2 Py-FeO2、Py-FeOOH 和ε-FeOOH 的晶格常數隨壓強的變化Fig. 2 Lattice parameters of Py-FeO2, Py-FeOOH and ε-FeOOH under high pressures

ε-FeOOH 的晶格常數在33 GPa 附近發生了突變，可能是ε-FeOOH 結構在壓強驅動下出現了氫鍵對稱化現象。氫鍵對稱化與壓強關系的相關研究表明，氫鍵對稱化現象會在30～40 GPa 的壓強驅動下在各種含有弱氫鍵的礦物相中產生，如冰的Ⅶ相、D 相、In-OOH 相以及含水硫化物系統等[44-47]。礦物中的羥基通常以不對稱結構的O―H···O 開始，氫原子通過強短共價鍵（O―H）與一個氧原子結合，氫原子與另一側的氧原子通過弱長氫鍵（H···O）結合。隨著深度和壓強的增加，羥基的共價鍵（O―H）延長，弱氫鍵（H···O）縮短，直到兩個鍵的長度相等，H 到達兩個相鄰氧原子的對稱中心。物質晶體結構在高壓下發生氫鍵對稱化現象，在具體數據中表現為羥基的共價鍵（O―H）和弱氫鍵（H···O）的鍵長變為O···O 鍵距離的一半[44]。

在33 GPa 以上，ε-FeOOH 結構中羥基的鍵長與O···O 鍵之間距離的一半幾乎相等，如圖3 所示。在ε-FeOOH 相這類含有弱氫鍵的體系中，常壓下O···O 之間的距離一般為2.6 ?，羥基的鍵長一般為1.0 ?；隨著壓強的增加，ε-FeOOH 的晶胞體積逐漸縮小，33 GPa 時，O···O 之間的距離逐漸縮小至2.338 ?；羥基的鍵長隨著壓強的增加反而逐漸延長，33 GPa時羥基的鍵長逐漸增加至1.170 ?，此時羥基鍵長為O···O 距離的一半；隨著壓強繼續增加（33 GPa之后），ε-FeOOH 結構中O···O 之間的距離和羥基鍵長繼續減小，羥基鍵長與O···O 距離的一半相等。

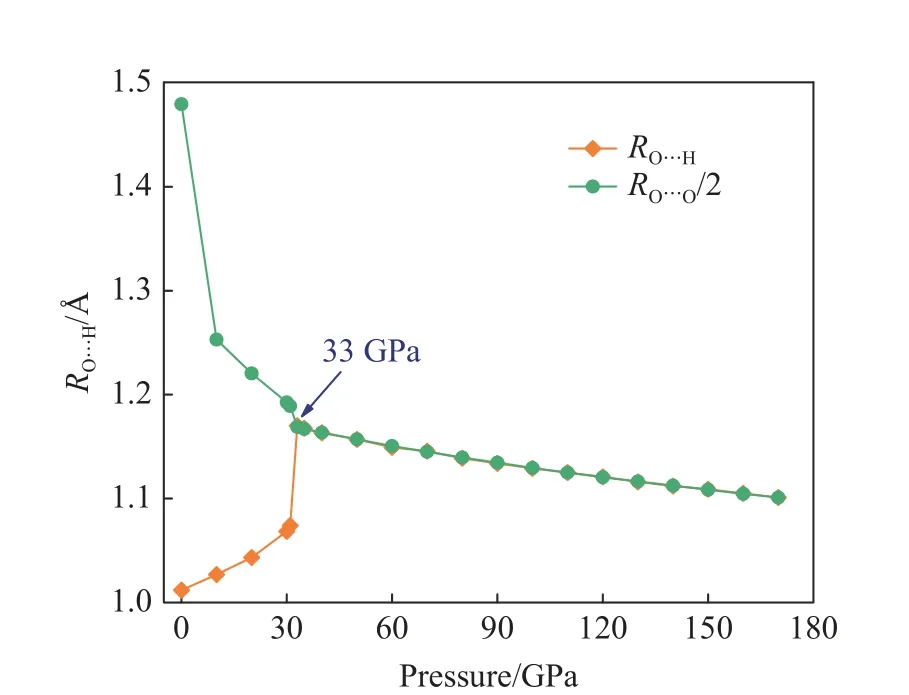
圖3 ε-FeOOH 結構中羥基鍵長和氧氧鍵長隨壓強的變化Fig. 3 Hydroxyl bond length and oxygen bond distance of ε-FeOOH under high pressures

P y-F e O O H 的結構中存在羥基，但P y-FeOOH 的晶格常數在30～40 GPa 沒有發生突變，原因是Py-FeOOH 晶體結構內不存在不對稱的O―H···O，而且在前人的實驗[6-7]中Py-FeOOH 的壓強（大于70 GPa）超過發生氫鍵對稱化的壓強條件（30～40 GPa）。Py-FeO2的結構內不存在羥基，結構中O―O 鍵長隨壓強變化的趨勢也與ε-FeOOH 結構不同，計算發現結構中O―O 鍵長隨壓強的增加逐漸減小（見圖4），與晶格常數隨壓強變化的趨勢相同。

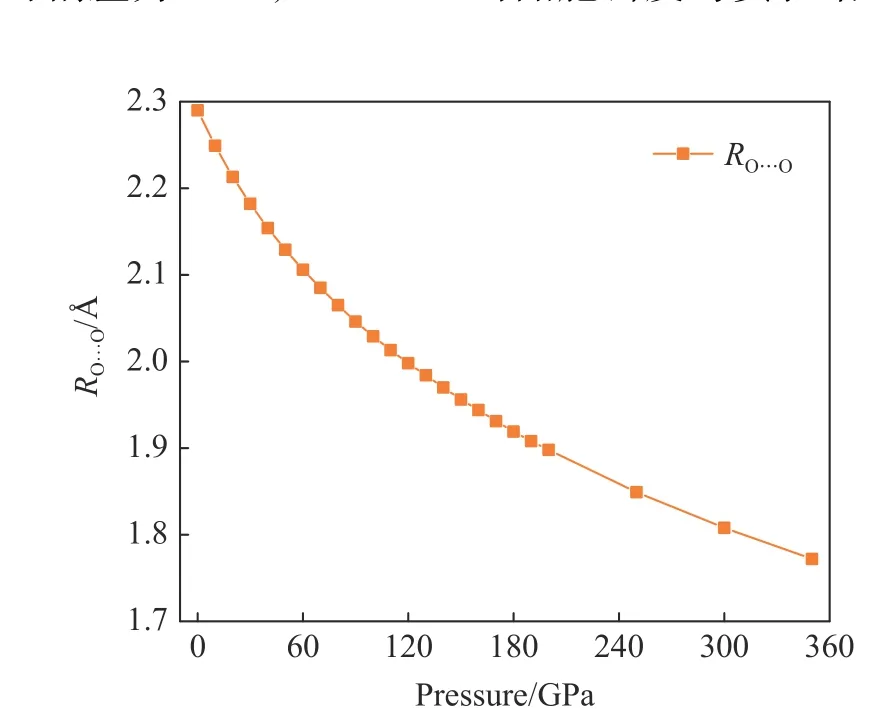
圖4 Py-FeO2 結構中氧氧鍵長隨壓強的變化Fig. 4 Oxygen bond length of Py-FeO2 under high pressures

Py-FeO2、Py-FeOOH 和ε-FeOOH 的晶胞密度隨壓強的增加而增加（見圖5），Py-FeO2、Py-FeOOH 和ε-FeOOH 的密度在同等壓強條件下依次減小，Py-FeO2的密度最高，Py-FeOOH 的密度比Py-FeO2降低9.4%，ε-FeOOH 的密度比Py-FeO2降低14.4%。計算得到的密度隨壓強的變化趨勢與實驗結果[5,7]基本相符，Py-FeO2的晶胞密度與實驗結果[5]的相對偏差為0.5%，Py-FeOOH的晶胞密度與實驗結果[7]的相對偏差為0.8%，ε-FeOOH 的晶胞密度與實驗結果[7]的相對偏差為2.5%。

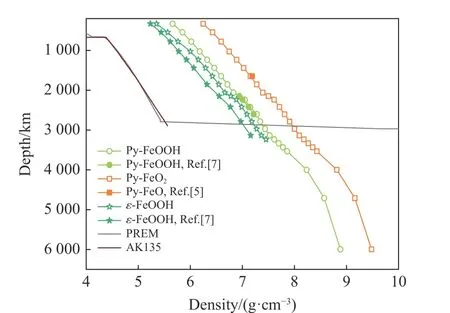
圖5 Py-FeO2、Py-FeOOH 和ε-FeOOH 的密度隨深度的變化Fig. 5 Variation of density of Py-FeO2, Py-FeOOH and ε-FeOOH with depth

在0～3 000 km 深度范圍內，Py-FeO2、Py-FeOOH 和ε-FeOOH 的密度高于典型地球密度結構模型（見圖5），與地幔的平均密度（5 g/cm3）相比[11]，Py-FeO2、Py-FeOOH 和ε-FeOOH 的密度更高。Py-FeO2、Py-FeOOH 和ε-FeOOH 的密度曲線在2 898 km（核幔邊界）附近與 PREM 和 AK135 模型相交，地球核部密度遠高于Py-FeO2、Py-FeOOH 和ε-FeOOH。與周圍的地幔相比，由于其明顯更高的密度，Py-FeO2、Py-FeOOH 將繼續向地球深部下沉。研究發現，在超過100 GPa 的壓強條件下，Py-FeO2、Py-FeOOH 會與AlOOH 和MgSiO4H2形成固溶體[7]，Tsuchiya 等[48]預測AlOOH 能以黃鐵礦型結構穩定存在至170 GPa，形成的固溶體會降低整個體系的密度，使之更接近PREM 模型。因此，Py-FeO2、Py-FeOOH 和ε-FeOOH 及固溶體的存在可能會對地幔的密度產生重要影響。

2.2 彈性性質

礦物的彈性性質是建立地球內部模型的重要參數，彈性性質包括彈性常數和彈性模量。為了研究Py-FeO2、Py-FeOOH 和ε-FeOOH 的彈性性質，分別計算了10～350 GPa 范圍內Py-FeO2和Py-FeOOH 以及0～170 GPa 范圍內ε-FeOOH 的彈性常數，結果見表1。

礦物的穩定性不僅包括能量的穩定性，還包括力學穩定性，力學穩定性可以采用Born-Huang 穩定性判據[49]進行判斷。

(1) Py-FeO2和Py-FeOOH 的結構是立方晶系，有3 個獨立彈性常數（C11、C12、C44），穩定性條件為：Cii＞ 0（i= 1, 4），C12＞ 0，C11-C12＞ 0，C11+ 2C12＞ 0。

(2) ε-FeOOH 的結構是正交晶系，有9 個獨立彈性常數（C11、C12、C13、C22、C23、C33、C44、C55、C66），穩定性條件為：Cii＞ 0（i= 1, 2, 3, 4, 5, 6），C11+C22+C33+ 2（C12+C13+C23） ＞ 0，C11+C22- 2C12＞ 0，C11+C33-2C13＞ 0，C22+C33- 2C33＞ 0。

Py-FeO2和Py-FeOOH 在0～350 GPa 內滿足立方晶系結構的穩定性條件，ε-FeOOH 在13～170 GPa范圍內滿足正交晶系結構的穩定性條件，表明它們均具有力學穩定結構。ε-FeOOH 是針鐵礦（α-FeOOH）、四方纖鐵礦（β-FeOOH）、纖鐵礦（γ-FeOOH）的高壓多形相。實驗和數值模擬研究證實，ε-FeOOH可以在約10 GPa 條件下形成，低壓下無法穩定存在[13-22]，與本計算結果（13 GPa）相符合。

Py-FeO2和Py-FeOOH 的彈性常數C11、C12、C44隨壓強的增加而線性增加（見圖6），整體上看，Py-FeOOH 的彈性常數大于Py-FeO2的彈性常數。Py-FeO2和Py-FeOOH 的彈性常數變化與前人結果[9-10]基本一致。ε-FeOOH 的彈性常數隨壓強的變化如圖6 和圖7 所示，其中C11、C12、C22、C33、C66、C13、C23隨著壓強的增加線性增加，C44隨壓強的增加而減小，C55隨壓強的增加變化不大。ε-FeOOH 的彈性常數在33 GPa 附近大幅變化，這是由于結構隨著壓強變化而產生了氫鍵對稱化現象。這一現象表明，ε-FeOOH 的彈性常數與氫鍵強度密切相關。對角彈性常數C44體現了晶格中（100）晶面沿著（010）晶向剪切應變的抵抗能力，（100）晶面上只有共邊的氧原子和氫鍵，彈性常數C44在高壓下的強度較低。壓強的增加使C44逐漸減小，意味著額外的壓力將導致ε-FeOOH 的結構穩定性降低。對于正交晶系結構的ε-FeOOH，需要滿足的穩定性條件為：Cii＞ 0 （i= 1, 2, 3, 4, 5, 6），C11+C22+C33+ 2（C12+C13+C23） ＞ 0，C11+C22-2C12＞ 0，C11+C33- 2C13＞ 0，C22+C33- 2C33＞ 0。因此，ε-FeOOH 能穩定存在的壓力邊界（170 GPa）被限定。

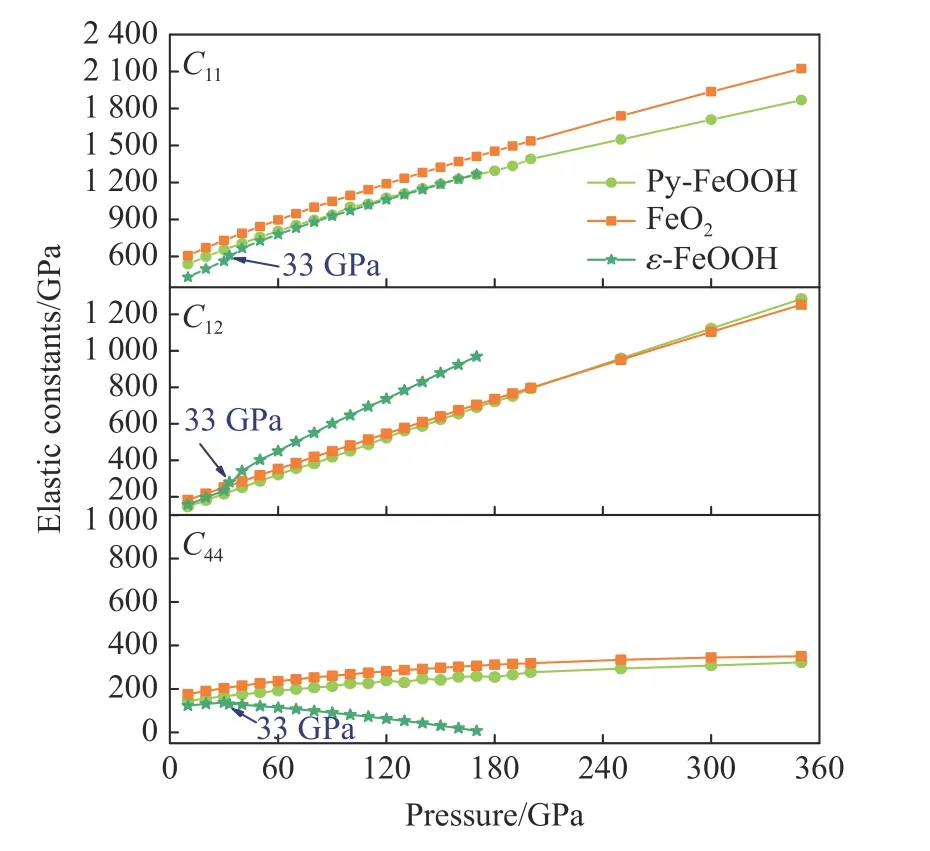
圖6 Py-FeO2、Py-FeOOH 和ε-FeOOH 的彈性常數（C11、C12、C44）隨壓強的變化Fig. 6 Elastic constants (C11, C12, C44) of Py-FeO2,Py-FeOOH and ε-FeOOH under high pressures

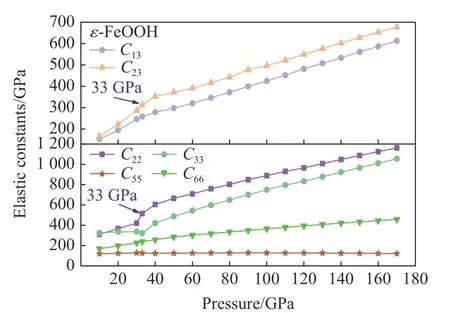
圖7 ε-FeOOH 的彈性常數（C13、C23、C22、C33、C55、C66）隨壓強的變化Fig. 7 Elastic constants (C13, C23, C22, C33, C55, C66) of ε-FeOOH under high pressures

物質的彈性性質通常還可以用體積模量（K）和剪切模量（G）表示，一般采用Voigt 模型和Reuss 模型計算得到。由Voigt-Reuss-Hill 理論[50]可知，Voigt 模型和Reuss 模型計算得到的彈性模量為多晶體彈性模量的上、下限，而Hill 模型則是兩者的數學平均，得到的計算結果與實驗值的一致性更好，因此本研究采用Hill 模型計算彈性模量。

Py-FeO2、Py-FeOOH 和ε-FeOOH 的體積模量和剪切模量隨壓強的變化見圖8。對比體積模量可知，Py-FeO2最高，Py-FeOOH 和ε-FeOOH 在高壓下幾乎一致；Py-FeO2的剪切模量最大，ε-FeOOH的剪切模量最小。Py-FeO2、Py-FeOOH 和ε-FeOOH的體積模量隨著壓強的增加線性增加，Py-FeO2和Py-FeOOH 的剪切模量隨壓強的增加線性增加。ε-FeOOH 的彈性常數C44隨壓強的增加而減小，剪切模量由彈性常數推導[45]可得（與C44的變化正相關），因而ε-FeOOH 的剪切模量呈現隨壓強增加而下降的趨勢。ε-FeOOH 的彈性模量在33 GPa 附近大幅增加，這是由結構內的氫鍵對稱化引起的。壓力誘導ε-FeOOH 結構發生氫鍵對稱化，提高了氫鍵的強度，致使彈性模量隨之增加。Py-FeO2、Py-FeOOH 和ε-FeOOH 的體積模量隨壓強變化速率大于剪切模量隨壓強變化速率。

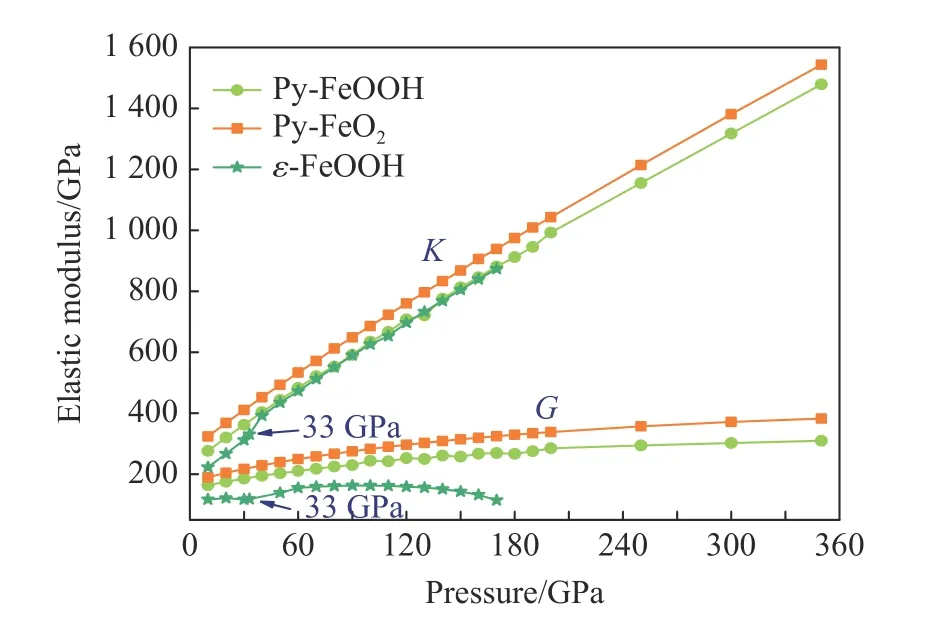
圖8 Py-FeO2、Py-FeOOH 和ε-FeOOH 的彈性模量隨壓強的變化Fig. 8 Bulk and shear moduli of Py-FeO2, Py-FeOOH and ε-FeOOH under high pressures

2.3 波速隨壓強變化的關系

Py-FeO2、Py-FeOOH 和ε-FeOOH 是地幔及核幔邊界的重要組成礦物，了解不同深度的地幔物質的物理性質，如密度、彈性性質和地震波速，可以更好地限定地幔物質的巖石學和化學組成模型。根據不同壓強下Py-FeO2、Py-FeOOH 和ε-FeOOH 的密度和彈性模量計算得到的剪切波速（vs）和壓縮波速（vp）如圖9 所示。與實驗數據[11,16]相比，Py-FeO2、Py-FeOOH 的剪切波速的相對偏差分別為32%和22%，壓縮波速的相對偏差分別為15%和6.8%。NRIXS 實驗與理論計算的絕對值相比有一定偏移，其原因在于在高壓和高溫條件下進行NRIXS 實驗極具挑戰性[11]。ε-FeOOH 的剪切波速的相對偏差約為6%，壓縮波速與Zhuang 等[13]的研究結果基本一致。

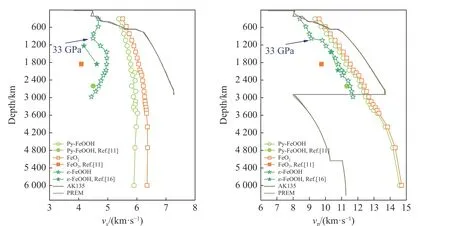
圖9 Py-FeO2、Py-FeOOH 和ε-FeOOH 的地震波速隨深度的變化Fig. 9 Variations of seismic wave velocities of Py-FeO2, Py-FeOOH and ε-FeOOH with depth

Py-FeO2、Py-FeOOH 和ε-FeOOH 的壓縮波速均隨壓強的增加而增加，Py-FeO2的剪切波速隨壓強的增加而增加，增加速率相對較小。Py-FeOOH 的剪切波速在0～2 000 km 深度范圍內隨深度的增加而增大，在2 000～6 000 km 深度范圍內變化較小（5.8 km/s ＜vs＜ 6.0 km/s）；ε-FeOOH 的剪切波速在33 GPa（深度約900 km）發生突變，在0～900 km 深度范圍內隨深度的增加而減小，在900～3 000 km 深度范圍內隨深度的增加先增大后減小。ε-FeOOH 在33 GPa 壓力下發生的氫鍵對稱化現象可能在一定程度上影響地幔過渡帶的密度和地震波速突變現象（從圖9 中可以看到波速突變）。ε-FeOOH 的剪切波速在50 GPa 之后再次出現波速隨壓力增大而減小的情況，但其壓縮波速卻呈現隨壓力增大而增大的趨勢，這是因為求解壓縮波速時方程中的體積模量遠遠大于剪切模量，削弱了結構變化帶來的影響。ε-FeOOH 的剪切波速發生了兩次波速軟化，可能與壓力誘導下ε-FeOOH 的結構相變有關。Thompson等[28]的最新研究表明，在0～75 GPa 壓力范圍內，ε-FeOOH 有兩次連續的結構相變，(18±1) GPa 時壓力誘導的氫鍵對稱化導致P21nm→Pnnm相變，在(45±2) GPa 經歷等結構的一級相變。ε-FeOOH 的兩次波速軟化很可能是兩次連續的結構相變導致的，具體分析還需要更多的數據支撐。

Py-FeO2、Py-FeOOH 和ε-FeOOH 的波速之間的大小關系顯示，ε-FeOOH 的波速最低，而Py-FeO2的波速最高。在地球深部，水的存在對地震波速有較大影響，計算結果表明，不含水的Py-FeO2波速明顯較高。Py-FeO2、Py-FeOOH 和ε-FeOOH 的波速曲線在400～700 km 深度范圍內與PREM 和 AK135 波速模型相交，在700～2 898 km（核幔邊界）深度范圍內的波速遠遠低于 PREM 和 AK135 波速模型。

綜合計算結果，可以發現，黃鐵礦型FeO2和FeOOH 具有高密度、低波速的特點，與地幔ULVZs 的性質一致。地核-地幔邊界區域的ULVZs 對地球的化學成分和熱結構具有重要影響，但它們的起源一直存在爭論[14]。如果Py-FeO2和Py-FeOOH 富集下沉到核幔邊界，可能會成為ULVZs 的來源。

3 結 論

運用第一性原理方法，計算了ε-FeOOH、Py-FeOOH 和Py-FeO2在不同壓強下的晶體結構變化和彈性性質。Py-FeO2和Py-FeOOH 的晶格常數隨壓強的增加呈現逐漸減小的趨勢，晶胞體積也隨著壓強的增加而降低。ε-FeOOH 的晶格常數整體變化趨勢是隨著壓強的增加逐漸減小，0～170 GPa 區間c軸長度相比a、b軸長度大幅減小，但在33 GPa 附近有異常突變，a、b軸長度突然增加，c軸長度突然減小。c軸上只有共邊的氧原子和氫鍵，相比有共邊的鐵原子以及鐵氧鍵的a、b軸，更容易被壓力誘導壓縮。Py-FeO2、Py-FeOOH 和ε-FeOOH 的晶胞密度隨壓強的增加而增加，Py-FeO2、Py-FeOOH 和ε-FeOOH 的密度在同等壓強條件下依次減小，Py-FeO2的密度最高。

Py-FeO2和Py-FeOOH 的彈性常數C11、C12、C44隨壓強增加線性增加；ε-FeOOH 的彈性常數C11、C22、C33、C66、C12、C13、C23隨壓強的增加線性增加，C44隨壓強的增加線性減小，C55幾乎不隨壓強變化。ε-FeOOH 的彈性常數在33 GPa 附近大幅變化，這是由于結構隨著壓強變化而產生的氫鍵對稱化現象。這一現象表明，ε-FeOOH 的彈性常數與氫鍵強度密切相關。Py-FeO2、Py-FeOOH 和ε-FeOOH 的體積模量以及Py-FeO2、Py-FeOOH 的剪切模量隨壓強的增加線性增加，ε-FeOOH 的剪切模量在33 GPa 突變升高。對比體積模量可知，Py-FeO2最高，Py-FeOOH 和ε-FeOOH 在高壓下幾乎一致；Py-FeO2的剪切模量最大，ε-FeOOH 的剪切模量最小。

Py-FeO2、Py-FeOOH 和ε-FeOOH 的壓縮波速隨壓強的增加而增加，Py-FeO2的剪切波速隨壓強的增加而增加。Py-FeOOH 的剪切波速在0～2 000 km 深度范圍內隨深度增加而減小，在2 000 ～6 000 km深度范圍內變化較小（5.8 km/s ＜vs＜ 6.0 km/s）；ε-FeOOH 的剪切波速在33 GPa（深度約900 km）發生突變。Py-FeO2、Py-FeOOH 和ε-FeOOH 的波速對比顯示，ε-FeOOH 的波速最低，Py-FeO2的波速最高。綜合研究發現，黃鐵礦型FeO2和FeOOH 具有高密度、低波速的特點，與地幔ULVZs 的性質一致。Py-FeO2和Py-FeOOH 在形成之后，可能會繼續富集下沉到核幔邊界，成為ULVZs 的來源。ε-FeOOH 在超過33 GPa 壓強條件下發生的氫鍵對稱化給ε-FeOOH 的結構帶來顯著變化，同時氫鍵對稱化會影響原子間相互作用，進而改變ε-FeOOH 的彈性性質和地震波速。

本研究豐富了Py-FeO2、Py-FeOOH 相在高壓下的彈性模量數據，為研究地球深部含鐵的含水礦物提供了新的數據支持，同時，對于高溫高壓下Py-FeO2、Py-FeOOH 和ε-FeOOH 及其固溶體在下地幔的賦存形式還需要開展深入研究，以探索其在地幔深部的賦存和對地幔物質組成和結構的影響。