沖擊加載下金屬鋁中氦泡演化行為的相場模擬

萬 曦，姚松林，裴曉陽

（中國工程物理研究院流體物理研究所沖擊波物理與爆轟物理重點實驗室, 四川 綿陽 621999）

材料在加工和儲存過程中不可避免地會產生缺陷。缺陷的存在可能顯著影響材料的力學性能，因此相關研究得到持續的關注。放射性環境下，材料可能遭受氦原子或氦離子等粒子的輻照，從而在材料中形成氦泡等缺陷[1-2]。已有研究表明，氦泡的存在會顯著影響材料的力學性能[3-6]，包括動力學性能和靜力學性能。早期的研究集中在準靜態研究領域，主要關注氦泡導致的氦脆與腫脹現象[3-7]。近年來，強動載荷下氦泡的行為與影響得到越來越多的關注[8-22]。強動載荷下材料的變形是一個超快動力學過程，力學響應一般呈現顯著的時間非平衡和空間非均勻等特性，相關研究十分復雜而困難。然而，受測量手段和實驗條件的限制，無法實時得到沖擊過程中材料內部的演化過程[23-25]。當前，人們主要通過測量強動載荷下材料的界面粒子速度獲得高時間分辨的動態變形信息，再結合樣品回收表征以及理論建模反推材料內部的變形過程[26-29]。

微介觀尺度下，人們主要通過表征回收樣品[14-15]或者原子模擬[18-20]獲得氦泡的演化規律及其對局域塑性變形的影響特征。Glam 等[17]通過表征回收樣品，發現沖擊加載前后氦泡出現明顯的聚集長大特征，這對深入認識損傷演化早期底層變形機理具有十分重要的意義。Shao 等[18]通過原子模擬對整個層裂過程中損傷形態的演化進行了研究，指出動態拉伸過程中大孔洞的形成源于小孔洞的匯合，而初始孔洞與氦泡的存在抑制了孔洞的長大。此外，Kubota 等[12]通過在模型中預設不同類型的初始缺陷，研究了不同類型的初始微缺陷及不同尺寸的氦泡對材料動態強度的影響；王海燕等[8]則對氦泡局域應力分布導致的位錯演化非均勻性進行了研究。

宏觀尺度下，人們通過測量速度波剖面，獲取了含孔洞材料的狀態方程、屈服強度以及拉伸強度，通過建立基于均勻化假設的唯象模型，對實驗現象進行了解釋。例如：Reisman 等[10]首先采用準等熵實驗獲得了孔隙度對輻照不銹鋼力學響應的影響規律，隨后通過建立含孔洞坍縮的演化方程，再現了因孔洞坍縮導致波剖面塑性前沿斜率顯著降低的關鍵特征。Raicher 等[13]建立了含氦泡鋁的狀態方程，并檢驗了氦泡的存在對材料沖擊加載響應的影響。Glam 等[17]采用沖擊加載手段對反應堆輻照摻硼鋁樣品的層裂強度進行了系列研究，結果表明，不同環境溫度下氦泡對層裂強度的貢獻呈現相反的趨勢，室溫下氦泡的存在導致層裂強度增大，而高溫下則導致層裂強度顯著降低。他們采用一個含氦泡內壓的唯象模型，再現了室溫下氦泡導致層裂強度增大的實驗現象，卻沒有明確指出導致該現象的原因。對于高溫下氦泡導致層裂強度減小的實驗現象，Glam 等則定性地指出，可能是由于氦泡的存在降低了塑性流動，同時有助于孔洞增長。

總的來說，當前對氦泡如何影響材料動力學行為的研究，無論是實驗還是理論模擬都相對較少。如何利用有限的實驗數據獲取更豐富的動態變形信息，對數值模擬工作提出了更高的要求。宏觀模擬完全忽略了微結構演化行為，對真實物理過程的描述不夠合理，且完全忽略了氦泡與位錯的相互作用。原子模擬可以有效地描述單個氦泡的演化行為及其對局域位錯演化的影響，但所能描述的時空尺度有限，且原子模擬結果難以給出氦泡演化行為對位錯集體演化行為的影響，進而限制了其為更大尺度力學響應特征提供理論支撐。

就動載下氦泡的演化行為而言，目前還缺少一個可以在更大時空尺度下考慮氦泡微結構效應，并可有效描述氦泡與位錯演化相互影響的模擬技術。在前期的工作中，我們已證實相場（phase field）方法可以有效描述沖擊下新相的生長過程，并能夠與宏觀力學響應有效關聯起來。類比新相生長過程，氦泡的生長過程同樣有望用相場方法描述，而晶體塑性理論可以在連續尺度描述塑性流動行為。為此，本研究將相場方法引入沖擊加載下氦泡的動態演化行為分析，通過與晶體塑性理論耦合，對沖擊加卸載過程中氦泡的演化行為及其對局域塑性變形的影響進行探討，以獲得規律性認識。相關研究可為解讀宏觀強度行為提供理論參考。

1 理論模型

在模擬材料的動態力學響應時，一般選用流體彈塑性模型描述[30]。基于流體彈塑性假設，可將變形拆分為球量響應和偏量響應，分別采用狀態方程和本構模型予以描述。本研究將在流體彈塑性理論框架下處理含氦泡鋁材料的力學響應。

分別建立不同的模型描述基體鋁材料和氦泡的力學響應，采用相場模型描述氦泡的演化，采用晶體塑性模型描述基體鋁材料的彈塑性響應。采用晶體塑性模型描述基體鋁材料的彈塑性響應的原因在于，大量的研究已經證實晶體塑性模型可以較合理地描述沖擊加載下材料的黏塑性響應，從而更加準確地預測氦泡/基體鋁材料界面處的應力分布，進而更加合理地描述氦泡生長行為。而選擇相場模型描述氦泡的演化行為則主要是由于相場方法具有強大的界面處理能力。下面將分別介紹相場模型和晶體塑性模型。

1.1 流體彈塑性分解

1.2 晶體塑性模型

晶體材料的塑性變形主要由位錯滑移和孿晶變形引起，而位錯作為塑性變形的基本單元在這兩種機制中都起著重要作用[34]。采用Orowan 方程可將宏觀層面的塑性應變率與微觀層面的位錯運動以及位錯生成關聯起來，其表達式為

采用Austin 等[38-39]提出的基于位錯亞結構演化的本構模型描述位錯密度演化，根據位錯在塑性變形過程中的作用將位錯區分為可動位錯和不可動位錯。可動位錯負責塑性滑移，不可動位錯負責控制材料的屈服應力，則有

1.3 基于相場方法的氦泡演化模型

相場模型是目前模擬材料微結構演化的重要的理論與計算工具。相場方法的優勢在于可以反映界面演化的動力學效應。基于擴散界面的思想可以有效避免求解具有運動邊界條件的微分方程組這一復雜的數學問題。相場模型借助序參量（場變量）將尖銳界面擴散為具有一定厚度的界面，界面的演化通過序參量的演化來實現[40-44]。

在求得序參量之后，就可以進一步求解壓力與溫度的演化。這里將壓力和溫度隨時間的變化率表示為比容和序參量隨時間變化率的函數，即

在實際計算過程中，考慮到氦泡內壓與物質密度均遠低于外加載荷，因此忽略氦泡物質密度以及內壓對計算結果的影響，即假設氦泡的密度和內壓均為零。在處理氦泡覆蓋的區域或氦泡/基體界面處相關力學參量時，物質密度、應力與內能均視為兩種材料的加權平均，即

2 計算模型

2.1 計算模型介紹

上述物理模型通過二次開發的二維有限元程序實現。其中，相場模型和晶體塑性模型已經在前期工作中應用于沖擊相變和動態塑性變形行為研究，模型的合理性及有效性得到驗證[28-29,44]。

對含氦泡鋁材料進行模擬研究，二維幾何模型如圖1 所示，模型寬1 μm，長5 μm。模型包括飛片和樣品，模擬從沖擊瞬間開始；模型下半部分為飛片，存在一個初始速度，即沖擊速度；上半部分為鋁樣品，初始速度為零。截取橫向足夠長鋁板中寬1 μm 的一段，左右邊界的橫向位移設置為零，上邊界為自由界面。模型網格大小為10 nm，橫向節點數為101，縱向節點數為501，總節點數為50 601。在模型中固定或隨機選取節點，設置初始序參量為1，即初始氦泡位置和大小，其他節點對應基體鋁材料，初始序參量設置為零。

2.2 模型參數

應用相場方法描述氦泡的演化，選用關鍵參數—動力學系數來控制界面演化速率，即氦泡生長速率。在有限元框架下，較大的變形將導致計算難以推進，為此選擇較小的動力學系數。不同的動力學系數描述的氦泡生長速率存在差異，但不影響對氦泡與位錯集體演化行為相互作用的規律性判斷。通過設置不同的飛片沖擊速度和動力學系數，發現氦泡增長速率與沖擊速度、動力學系數正相關，需要通過設置沖擊速度和動力學系數避免氦泡生長過快。經過對比，選取沖擊速度為100 m/s、動力學系數L=500進行模擬。晶體塑性模型相關參數在前期工作中有詳細討論。

計算中所使用的材料參數和模型參數如表1、表2、表3 和表4 所示。表1 列出了金屬鋁的狀態方程與聲子拖曳系數等參數，B0為室溫聲子拖曳系數，B′T為聲子拖曳系數關于溫度的導數。表2 列出了金屬鋁的彈性常數（c11、c12、c44）及其關于溫度的導數（dc11/dT、dc12/dT、dc44/dT）。表3 列出了晶體塑性模型參數，αHN為參考成核速率，αMult為無量綱模型參數，αanni為表征湮滅速度的無量綱參數，vI為俘獲過程中的特征速率，ρinitial為初始位錯密度，模型參數的確定參見文獻[45]。表4 列出了相場模型參數。

表1 狀態方程參數與聲子拖曳系數Table 1 Parameters of equation of states and phonon drag coefficients

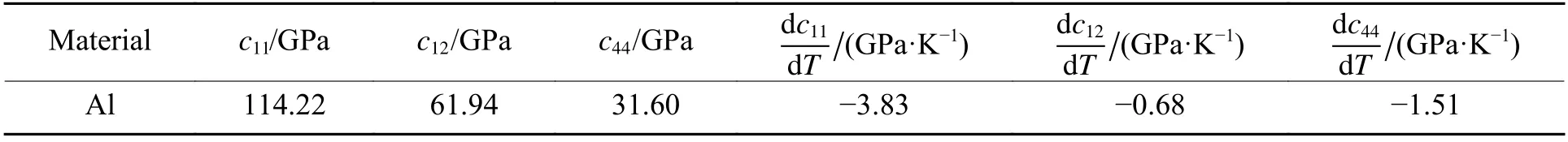
表2 彈性常數及其關于溫度的導數Table 2 Elastic constants and temperature derivatives of the elastic constants

表3 晶體塑性模型參數Table 3 Parameters of the crystal plasticity model

表4 相場模型參數Table 4 Parameters of the phase field model

3 計算結果與分析

本研究模擬的實驗構型為飛片撞擊樣品，飛片與樣品相互作用后，在界面處分別向樣品和飛片中發射沖擊波，沖擊波與飛片后界面和樣品自由面作用后，反射稀疏波。兩束稀疏波在樣品中相遇，產生拉應力，導致局域孔洞或氦泡生長和聚集，最終形成層裂。圖2 為應力波的傳播示意圖。

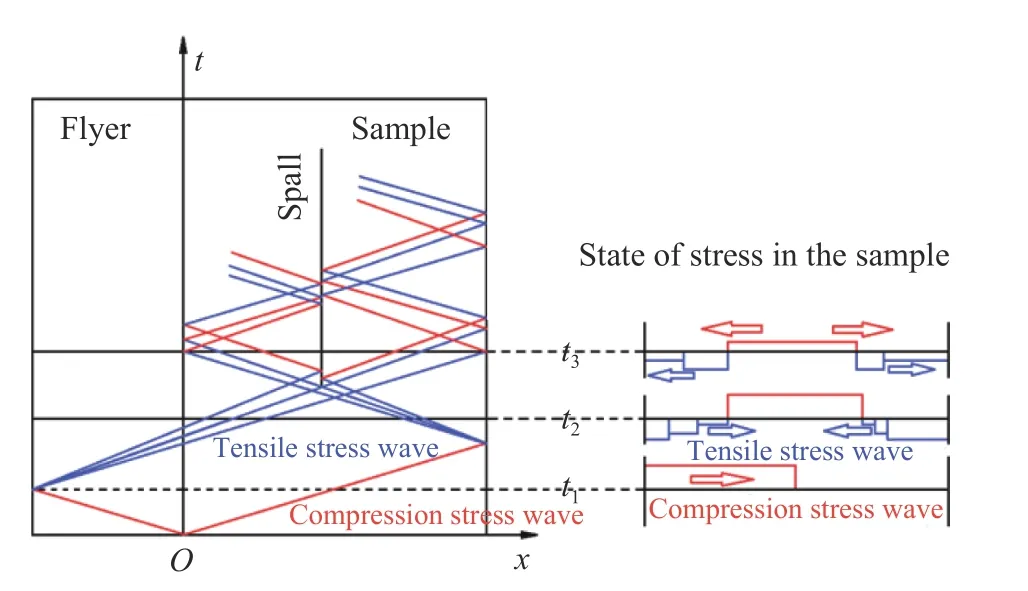
圖2 應力波傳播示意圖Fig. 2 Schematic diagram of evolution of stress wave

應用上述模型，對沖擊下金屬鋁中的氦泡演化行為及其對局域位錯集體演化行為的影響進行了數值模擬研究。主要研究內容包括3 個部分：氦泡的結構非均勻性、沖擊下單個氦泡的生長行為以及兩個或多個氦泡的聚集長大行為。

3.1 氦泡的結構非均勻性

首先模擬分析了沖擊壓縮過程中單個氦泡與沖擊波的相互作用。模擬結果表明，沖擊波到達后，氦泡的結構非均勻性導致局域應力集中和塑性變形集中。從分切應力云圖可以看出，分切應力最大值集中在4 個對角線方向，對應剪應力最大方向，如圖3 所示。

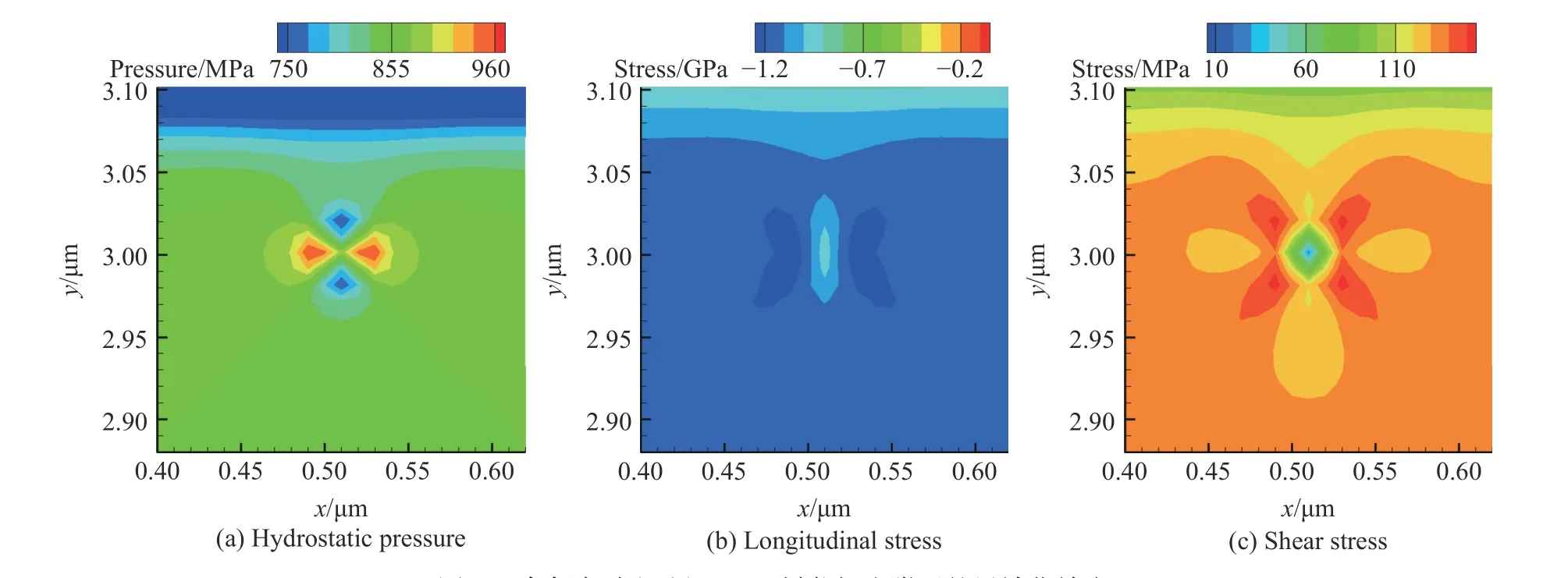
圖3 沖擊波到達后（0.1 ns 時刻）氦泡附近的局域化效應Fig. 3 Localization effect near the helium bubble at the arrival of the shock wave (0.1 ns)

從計算結果中提取了沖擊壓縮過程中位錯密度的演化歷史，如圖4 和圖5 所示。計算結果表明，可動位錯密度主要集中在撞擊面附近以及氦泡的4 個對角線方向，最大位錯密度約為1015m-2。特別地，氦泡附近4 個對角線方向對應剪應力最大值方向。隨著應力波在樣品中反復傳播，氦泡對角線方向高位錯密度區域逐漸擴展，同時氦泡周圍的位錯密度不斷累積，在二維空間內逐漸將對角線方向高位錯密度區域連接起來，如圖5 所示。

除變形局域化以外，計算結果表明，氦泡的存在還會導致應力波傳播發生改變。沖擊波與氦泡相互作用會導致沿沖擊波傳播方向發射稀疏波，沿垂直于沖擊波傳播方向發射壓縮波，體現為氦泡附近縱向區域的壓力低于鋁基體區域，而橫向區域的壓力高于鋁基體區域，如圖3(a)和圖3(b)所示。

氦泡與沖擊波相互作用引起的應力波傳播改變與于繼東[40]模擬的相變微結構與沖擊波相互作用的結果一致。根據Yao 等[45]和Gurrutxaga-Lerma 等[46]最新的動態塑性變形研究結果可知，沿縱向發射的稀疏波實則為沖擊波陣面上塑性松弛所發射的稀疏波。由于波后區域是超聲速的，Gurrutxaga-Lerma 等在研究“彈性前驅衰減”現象時指出，該稀疏波會追趕上沖擊波前，導致“彈性前驅衰減”現象出現。基于該認識，可以預期，氦泡與沖擊波相互作用發射的稀疏波最終也會追趕上沖擊波前，并導致彈性前驅進一步衰減。該研究結果能夠解釋Glam 等[17]在實驗中發現的含氦泡摻硼鋁的動態屈服應力略低于不含氦泡摻硼鋁，即含氦泡材料的動態屈服應力略小于不含氦泡材料的動態屈服應力。

3.2 沖擊下單個氦泡的生長行為

Glam 等[17]對含氦泡摻硼鋁材料進行了沖擊實驗，結果顯示沖擊后氦泡出現長大特征。在本研究的模擬過程中，如果不對氦泡在應力波傳播過程中的演化行為做任何限制，氦泡會在沖擊壓縮波的作用下出現變形，模擬結果趨于不可控，與前人的實驗結論背離，因此基于前人實驗得出的氦泡演化物理圖像，限定氦泡僅在拉伸應力的作用下長大，在壓應力的作用下不發生演化。從計算結果中提取氦泡尺寸隨時間的變化關系，并對時間求微分，從而獲得了氦泡長大速率隨時間的變化關系。在統計氦泡尺寸時，將序參量大于0.5 的區域確定為氦泡的直徑，即半高全寬法。

計算結果表明，卸載波到達前，氦泡直徑幾乎不發生變化，如圖6 所示，0.5 ns 時序參量分布幾乎與開始時設置的序參量分布相同，與真實的物理圖像一致。由圖7、圖8 和圖9 可知，氦泡的生長行為在卸載波到達后才較為顯著，生長速率（dR/dt）在第1 次與第2 次卸載波到達時最大。隨后，氦泡的生長速率迅速衰減，后期氦泡尺寸幾乎不發生變化。圖9 中縱向剪應力演化歷史與氦泡生長速率演化相對應：壓縮波到達后，剪應力迅速上升，塑性變形導致剪應力最終被松弛至屈服面，壓縮應力作用下氦泡不發生演化；稀疏波到達后，剪應力反向增大，拉伸剪應力作用下氦泡的生長速率迅速增大；隨著沖擊波在材料中不斷傳播和反射，剪應力幅值不斷下降，氦泡的生長速率不再顯著。

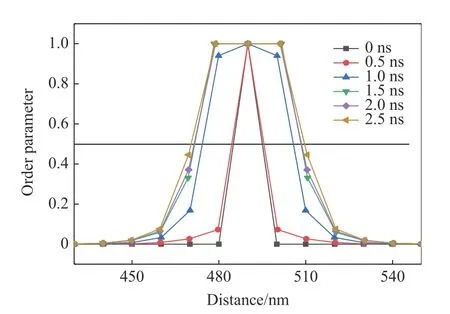
圖6 不同時刻氦泡序參量的空間分布Fig. 6 Spatial distribution of order parameter at different times

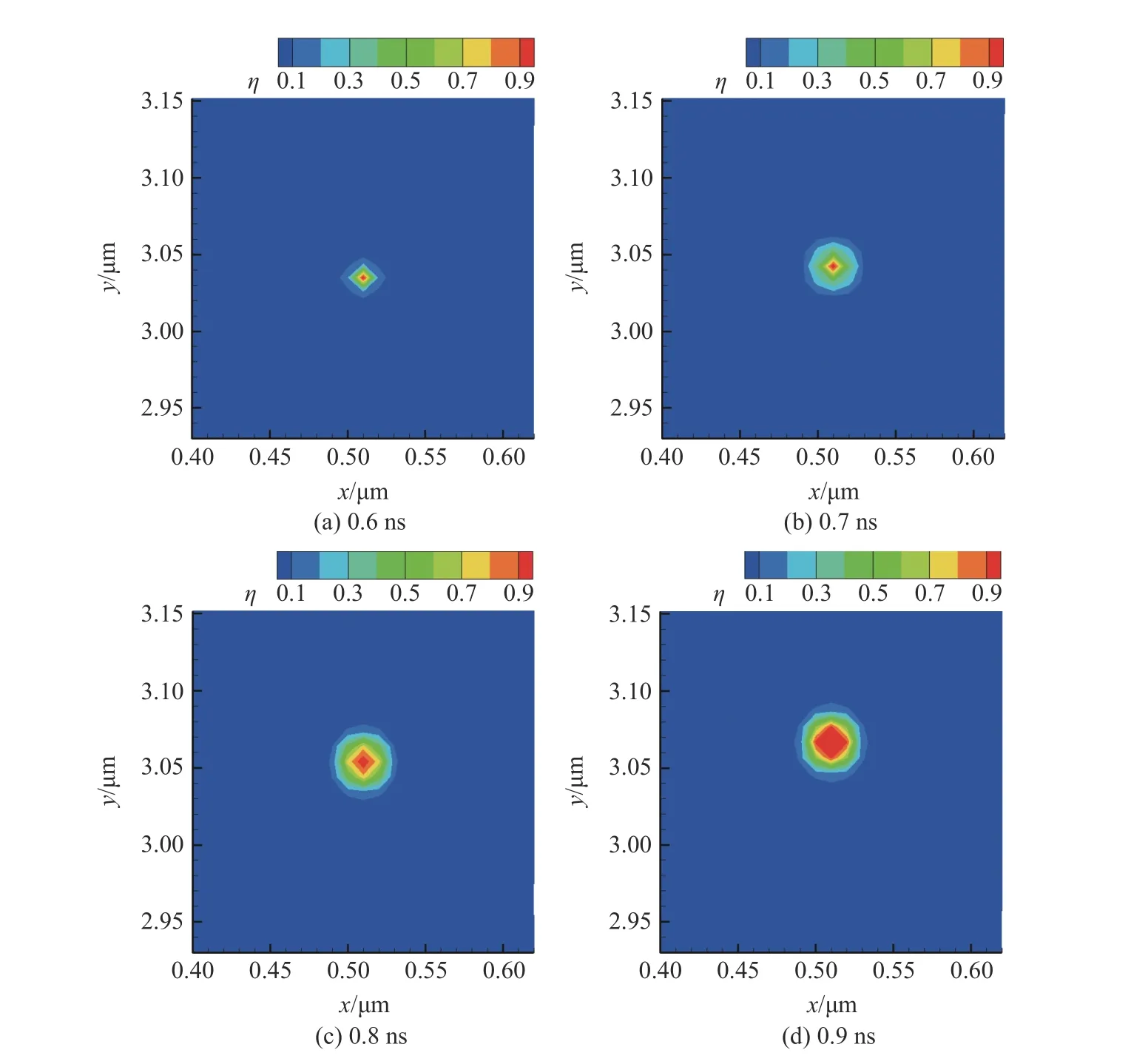
圖7 第1 次與第2 次卸載波到達后氦泡的演化行為Fig. 7 Evolution of helium bubbles when the first and second unloading waves arrive

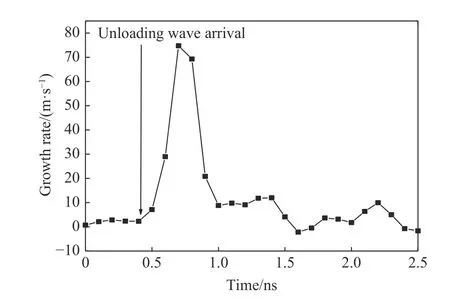
圖8 氦泡生長速率隨時間的變化關系Fig. 8 Time history of the growth rate of helium bubbles

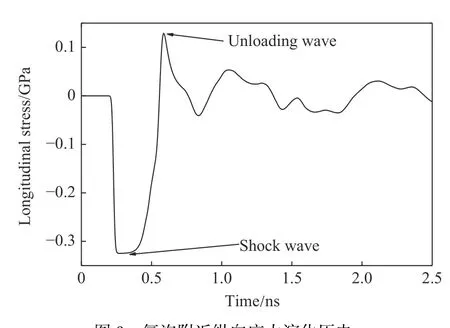
圖9 氦泡附近縱向應力演化歷史Fig. 9 Time history of longitudinal shear stress near the helium bubbles

從能量的角度來講，隨著沖擊波在樣品中不斷傳播與反射，塑性耗散和氦泡演化共同導致能量耗散，卸載波初次到達氦泡所在區域時所攜帶的能量最大，為氦泡快速生長提供了條件，氦泡快速生長不斷消耗卸載波所攜帶的能量，使卸載波攜帶能量急劇降低，進而導致氦泡演化驅動力減小，因此氦泡的生長速率在卸載波到達后達到極大值，隨后發生顯著衰減。

3.2.1 塑性模型對氦泡演化行為的影響

采用理想彈塑性模型和晶體塑性模型計算的氦泡長大行為存在差異，對比結果如圖10 所示。可見，采用晶體塑性本構模型計算的氦泡長大速率更快。

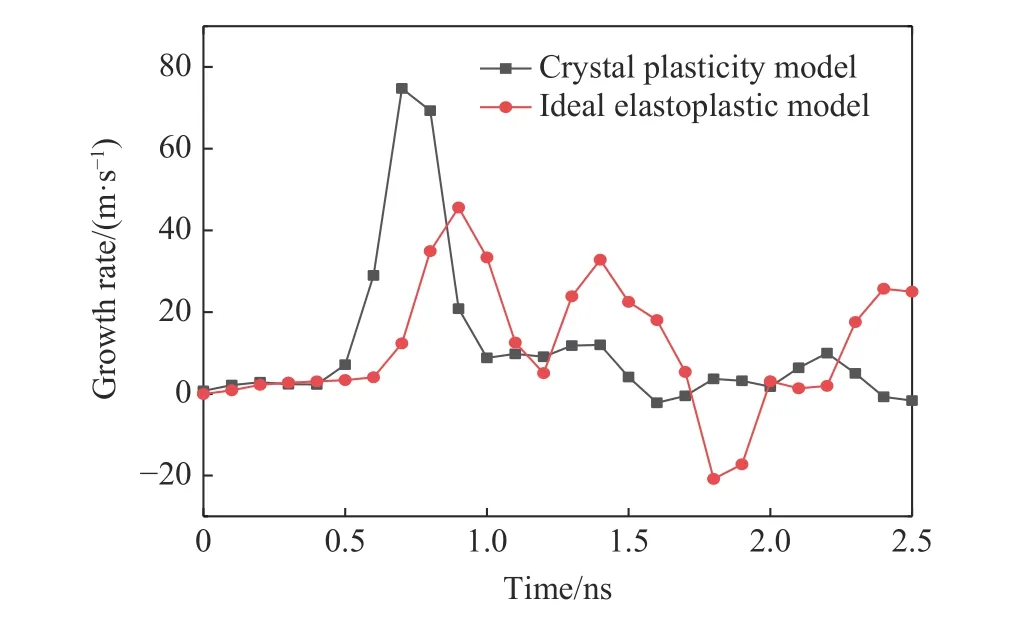
圖10 在300 K 環境溫度、100 m/s 的加載速度下不同模型模擬的氦泡長大速率Fig. 10 Growth rates of helium bubbles simulated by different constitutive models at 300 K and impact velocity of 100 m/s

晶體塑性模型與理想彈塑性模型的最大差異在于對屈服行為的描述。在理想彈塑性模型中，剪應力松弛至屈服的過程瞬間發生并完成，因此應用該模型計算時剪應力始終處于較低水平。而黏塑性本構模型中，剪應力的松弛是一個弛豫過程：在彈性前驅波作用下，剪應力迅速上升，有限的位錯滑移來不及將剪應力迅速松弛下來；塑性沖擊波到達后，一方面塑性壓縮使剪應力不斷增加，而塑性松弛又使剪應力不斷減小；隨著位錯密度的累積，塑性松弛效應主導剪應力演化，剪應力迅速下降，直至達到臨界分切應力[23,25]。該過程對應整個沖擊前沿，在該過程中剪應力得以更多地參與到驅動氦泡長大。因此，采用黏塑性本構模型計算的氦泡長大速率高于采用理想彈塑性模型的計算結果，從而進一步表明一個準確的塑性本構模型對描述非均勻微結構演化行為和影響的重要性。

3.2.2 溫度對氦泡演化行為的影響

采用同樣的構型和模型參數，計算了600 K 環境溫度下氦泡的演化行為，并與室溫下氦泡的演化行為進行了對比，如圖11 所示。計算結果表明，氦泡的生長速率隨溫度的升高而增大。該現象可以歸因于聲子拖曳機制主導沖擊加載下的位錯運動。在研究FCC 金屬的動態屈服應力熱硬化現象時，Yao 等[45]指出，聲子拖曳機制作用下，位錯運動速率隨溫度的升高而降低，塑性耗散速率更低。塑性耗散速率的改變會導致氦泡演化的驅動力Gibbs自由能發生改變

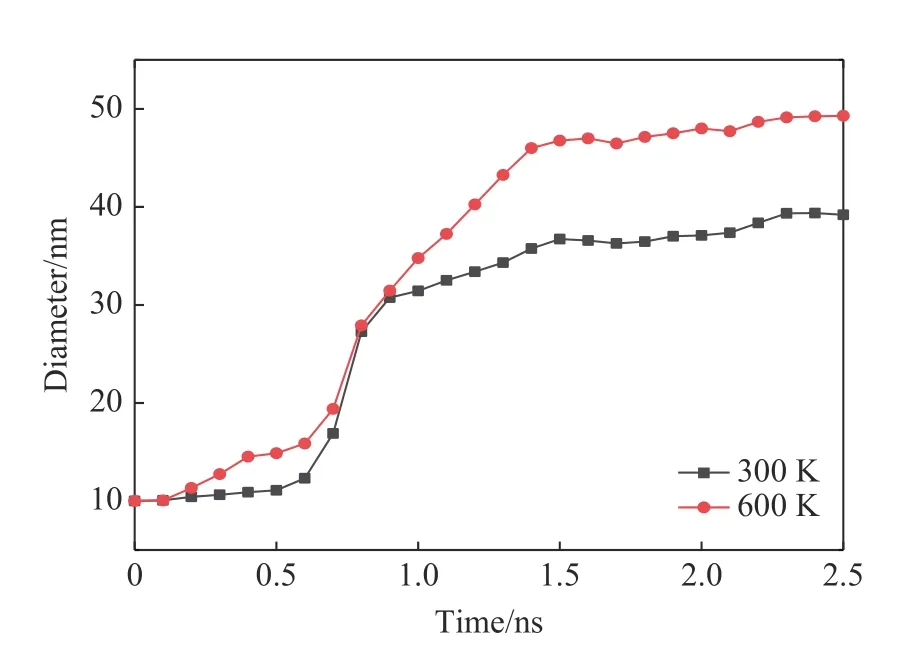
圖11 不同環境溫度下氦泡生長速率對比Fig. 11 Comparison of growth rates of helium bubble at different ambient temperatures

3.2.3 初始位錯密度對氦泡演化行為的影響

為探究不同初始位錯密度對氦泡生長行為的影響，選取初始位錯密度分別為1011和1013m-2，模擬了氦泡生長速率隨時間的變化，計算結果如圖12 所示。對比氦泡生長速率隨時間的變化關系可知，初始位錯密度越高，氦泡的生長速率越慢。這仍然可以從能量的觀點解釋，更多的初始位錯將消耗更多的剪切應變能，因此用于驅動氦泡生長的剪切應變能更少。

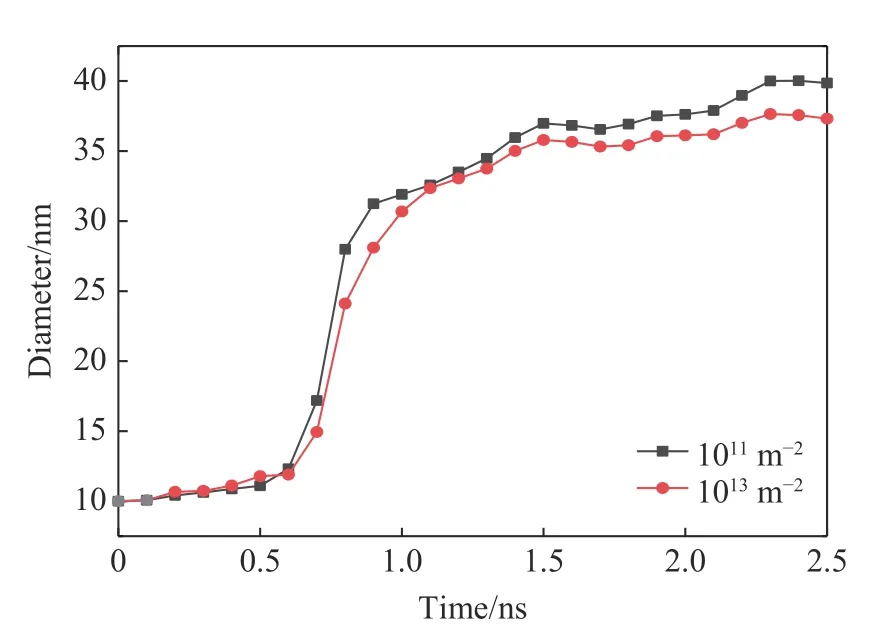
圖12 不同初始位錯密度下氦泡生長速率的對比Fig. 12 Comparison of growth rates of helium bubble under different initial dislocation densities

3.3 兩個或多個氦泡的聚集行為

Glam 等[17]對比沖擊前后鋁材料中的氦泡尺寸發現，沖擊載荷作用下氦泡尺寸顯著增大。根據氦泡演化的物理圖像可知，氦泡生長一方面源于拉應力作用下氦泡自身的發展，另一方面則是由于小氦泡聚集融合形成大氦泡，為此模擬了兩個或多個氦泡的聚集長大行為。受所使用方法的限制，彈塑性模型僅能模擬動力學系數最大值為500 時的氦泡演化過程，而在模擬兩個或多個氦泡時，設置動力學系數為500 時模擬結果顯示的氦泡生長行為不顯著，因而將動力學系數提高到800，設置溫度為600 K 進行模擬，使氦泡的生長行為更加顯著。盡管如此，計算結果仍然能夠定性地反映兩個或多個氦泡的長大聚集行為。

如圖13 所示，用序參量η 的分布表示不同相態氦泡與基體的分布，計算結果能夠描述兩個相鄰氦泡的長大聚集過程。盡管兩個氦泡的初始位置關于沖擊加載方向左右對稱，且其他條件完全相同，但是從氦泡的演化過程來看，兩個相鄰氦泡的演化行為并不完全一樣，左氦泡的長大速率略高于右氦泡。考慮到兩個氦泡所處的初始條件和加載條件一致，因此推斷氦泡生長過程對周圍的影響存在一定的范圍，當兩個氦泡相距足夠近時，生長過程中會出現能量競爭現象，進而導致生長速度不一致，即相鄰氦泡的演化存在競爭關系。

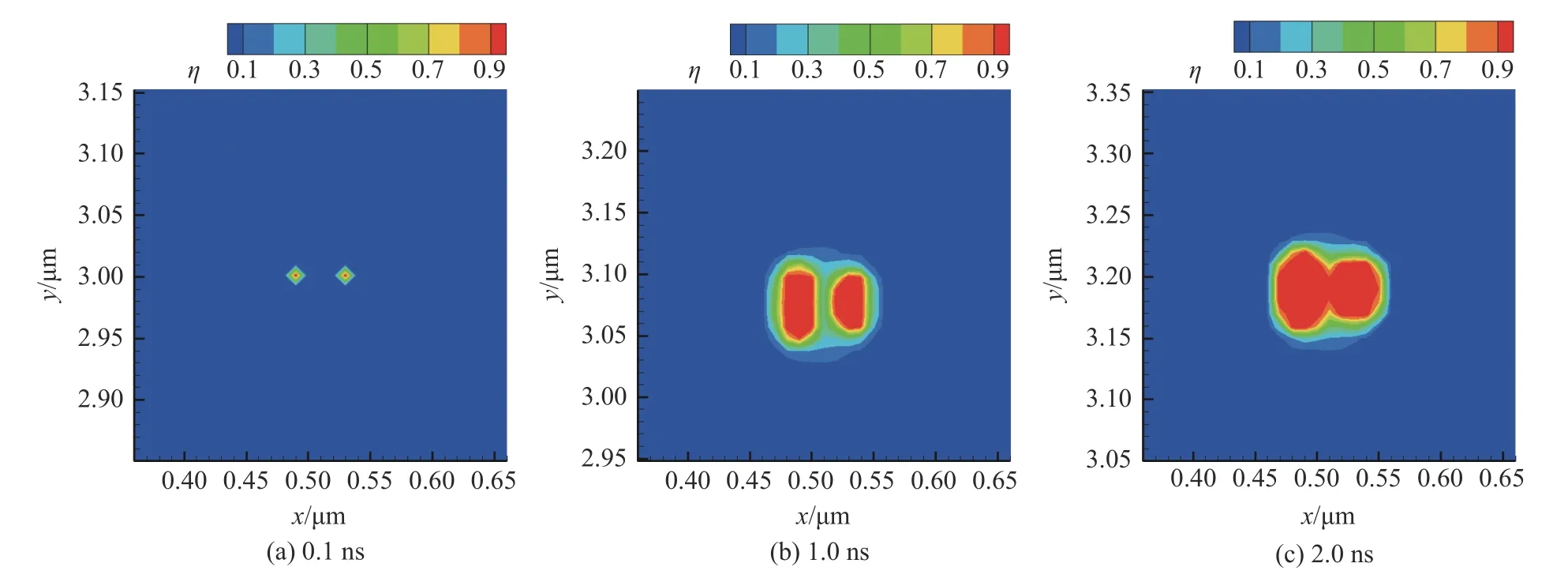
圖13 兩個氦泡的長大聚集過程Fig. 13 Growth and aggregation of two helium bubbles

盡管兩個氦泡的演化行為存在差異，但是兩個氦泡附近的剪應力和局域塑性變形并沒有呈現明顯的非對稱性，包括局域塑性變形、臨界分切應力分布等，如圖14 所示。對此，分析認為當兩個氦泡相距足夠近時，氦泡結構非均勻性導致的應力局域化和單個氦泡的作用效果近似一致。

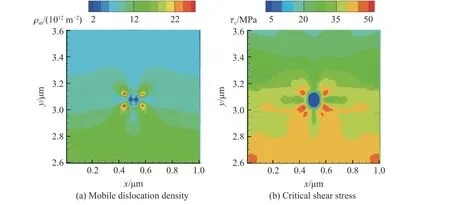
圖14 1.0 ns 時刻氦泡附近的可動位錯密度與臨界分切應力分布Fig. 14 Contours of mobile dislocation density and critical shear stress near helium bubble at 1.0 ns

此外，對比了距離較遠的兩個氦泡的演化行為，兩個氦泡的初始位置仍然關于沖擊加載方向左右對稱。計算結果表明，距離較遠的兩個氦泡的長大過程不會出現明顯差異，側面證明了氦泡生長過程對剪切應變能的消耗存在一定的范圍，如圖15 所示。

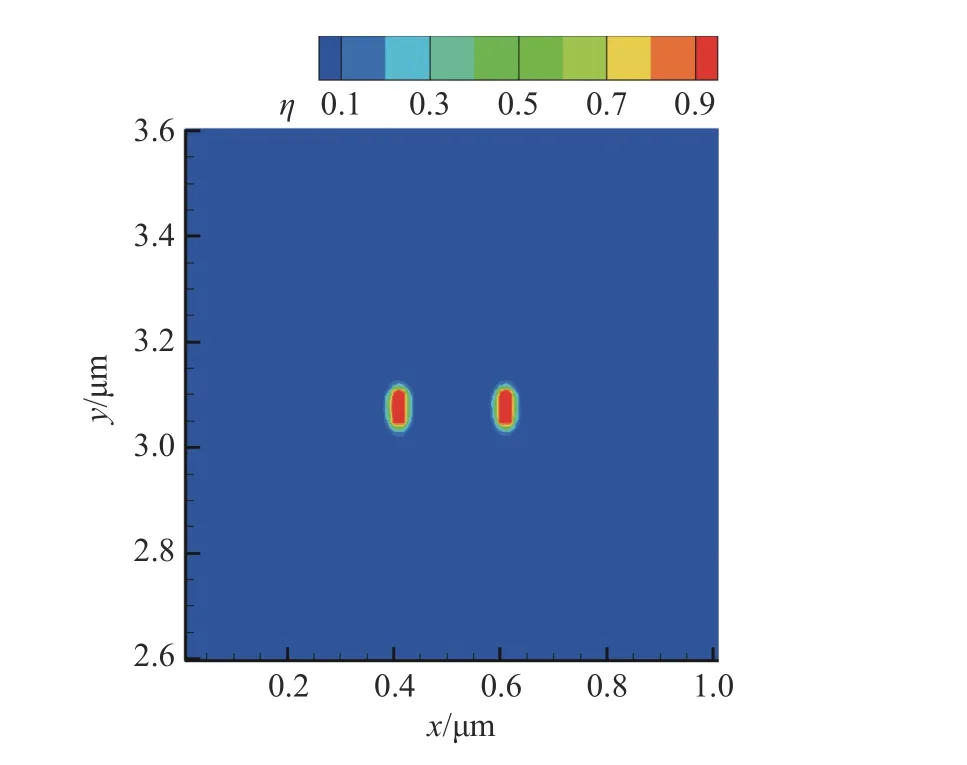
圖15 兩個氦泡距離較遠時1.0 ns 時刻的序參量分布Fig. 15 Distribution of order parameters at 1.0 ns when two helium bubbles are far apart

當預置很多氦泡時，受沖擊后氦泡的生長和聚集行為如圖16 所示。可以看出，氦泡的演化行為和前面所得結果一致，在壓縮波的作用下氦泡幾乎不生長，卸載波到達后氦泡尺寸出現明顯的變化。從演化結果可以得出：由于氦泡之間的相互作用以及氦泡對周圍應力分布的影響，當氦泡較多、分布較密時，氦泡聚集主要發生在沖擊波傳播方向。

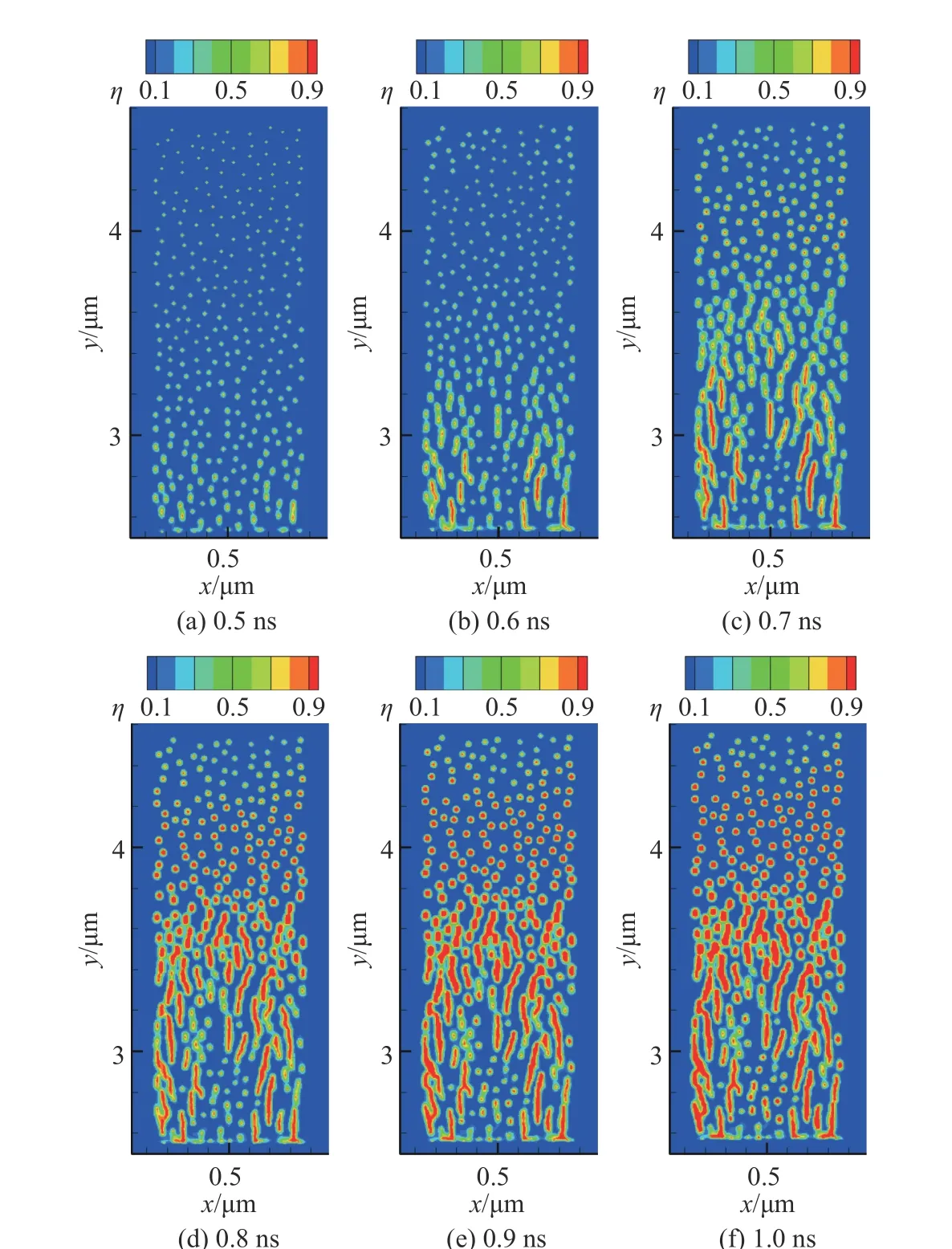
圖16 較多初始氦泡時的沖擊演化行為Fig. 16 Impact evolution behavior of more initial helium bubbles

4 總 結

基于相場方法建立了可描述沖擊下氦泡演化的物理模型，并應用該模型研究了不同外加條件下氦泡的長大行為及其對局域位錯集體演化行為的影響。結果表明：氦泡的結構非均勻性會導致局域應力集中和塑性變形集中；在與沖擊波相互作用的過程中，局域塑性變形沿沖擊波傳播方向發射稀疏波，該稀疏波與塑性松弛過程發射的稀疏波共同導致動態屈服應力減小。從氦泡的生長行為來看，氦泡的生長與塑性變形呈競爭關系。在輸入剪切應變能一定的情況下，更大的氦泡密度以及更快的生長速率會消耗更多的剪切應變能，導致塑性變形量更小，表觀強度更大；反之，更快的塑性變形速率導致氦泡生長更慢，進而使層裂強度更大。盡管如此，由于氦泡本身是一種微觀缺陷，因此暫時無法直接將其演化行為與宏觀力學響應聯系起來。另外，受限于有限元方法處理大變形的能力，目前暫時只能對早期的氦泡演化行為進行研究，無法模擬氦泡聚集并貫通這一物理過程。