問題驅動數學教學的基本原則與思想及其實施步驟

王海青，曹廣福

問題驅動數學教學的基本原則與思想及其實施步驟

王海青1，曹廣福2

（1．惠州學院 數學與統計學院，廣東 惠州 516007；2．廣州大學 數學與信息科學學院，廣東 廣州 510006）

問題是促動學科發展的原始動力，數學也不例外．問題驅動數學教學研究依據課程標準“要創設合適的教學情境，提出合適的數學問題”的要求，進行相應的理論思考和實踐探索．問題驅動數學教學的關鍵是創設真實的問題并賦予問題有效的情境，教師引領學生在問題情境空間中探究生成數學知識，習得數學思想方法并學會思考．基于問題驅動理論與數學學科的特點剖析問題驅動數學教學的基本原則和基本思想，構建針對具體課時的問題驅動教學實施步驟，為教學的設計與組織提供參考．

問題驅動；問題情境；數學教學；數學思想

1 問題驅動與數學教學

由于數學的特點和教材編寫的需要，數學教科書基本上是以概念的描述、定理的證明、法則的論證等構成形式化的邏輯演繹體系，而知識產生的原始問題與豐富背景都幾乎消失殆盡．這使學習者在一堆符號化的邏輯推理中很難體會到所蘊含的數學美及其重要價值．但“數學并不是按照教科書中的方式發展的”[1]．問題是促進學科發展的原始動力，數學也不例外．M. Kline就曾指出：“每一個數學分支均是為攻克一類問題而發展起來的．”[2–3]因此，合乎情理和邏輯的數學教學也應圍繞問題展開．

《普通高中數學課程標準（2017年版）》[4]強調“教學活動應該把握數學的本質，創設合適的教學情境，提出合適的數學問題……教學情境包括現實情境、數學情境、科學情境”，并指出“情境創設和問題設計要有利于發展數學學科核心素養”．教師需通過問題與情境引導學生經歷知識的生成過程，揭示數學的本質并學會思考．要求設計合適的教學情境和數學問題為學生提供具有挑戰性的實踐創新平臺，問題驅動數學教學研究也正是基于課程標準的要求進行相應的理論和實踐探討．問題驅動教學的實質就是指要創設真實的問題并賦予有效的情境，教師引領學生圍繞問題情境探究發現，在解決問題的過程中體驗數學的“再發現”過程，習得具體的知識獲得相應的數學思想方法[5]．

以問題驅動教學，能再現數學豐富多樣的“火熱”思考過程，揭示數學本質并教學生學會思考；以問題驅動教學，有助于學生在問題情境中從事探索活動，在經歷數學發現的過程中生成“形式化”的數學概念與原理并習得數學思想方法．數學教育家張奠宙先生曾提出“以問題驅動的新概念數學”[6]，李大潛院士也大力提倡“問題驅動的應用數學研究”[7]，還有許多文獻從不同的角度探討了問題驅動下的數學教學[8–11]．2018和2019年出版的著作《問題驅動的中學數學課堂教學》[5，12–13]的理論與實踐卷、概率與統計卷、復數與三角卷系統地探討了問題驅動教學理論及其在中學數學課堂上的應用．

2 問題驅動數學教學的基本原則

問題驅動數學教學遵循“由問題到理論”，是對荷蘭數學教育家弗賴登塔爾“再創造”思想的具體化．弗賴登塔爾認為任何數學都是“數學化”的結果，學數學就是學“數學化”的過程[14]．從現實情境發現問題并抽象出數學模型或數學問題的符號化過程稱為“橫向數學化”．從不同角度和層次分析、表征與解決數學模型或問題的形式化過程稱為“縱向數學化”．但弗賴登塔爾的數學教育觀主要從學生認知層面強調教學組織過程，根據學生的“數學現實”將一系列的教學材料通過“再創造”將之“數學化”地組織起來，即“如何教”．問題驅動教學除了關注“如何教”，也重視“教什么”與“為什么教”．它從教育哲學層面深入到數學內部去剖析知識的背景與價值，進而創設能反映本質，符合學生實際的問題與情境驅動教學，使學生經歷完整的“數學化”過程．

數學的產生與發展在解決現實問題、科學問題和內部矛盾的過程中逐步完善．所以，數學概念或原理的形成可以是源于現實生活、自然與工程等科學或者是數學本身的問題．只要是“具有啟發性的、本原性的、觸及數學本質、能夠在教學中起統帥作用的”[6]問題都是好問題、真問題．真問題又常劃分為“本原性問題”和“派生性問題”兩類[9]：前者指促使事物產生的最初根源，后者是指某個數學理論產生之后根據自身邏輯發展產生的問題．問題有助于數學本質的揭示，但“問題不等于問題情境”[15]，只有當學生面對問題有解決它的心向和欲望——即具備有意義學習的條件時，問題才能構成問題情境，才能真正做到以問題驅動教學．從數學的發展史看，有效的問題情境材料應“具有一定的生活意義、數學價值或科學價值”[9]．要創設恰當的問題及其情境，需追溯數學史回答以下3個問題：這個內容當初是怎么產生與發展的？人們為什么要去研究它？它有什么價值？通過歷史挖掘承載在具體數學知識之上的問題背景、思想方法以及數學家的研究精神．由此可見，基于問題驅動的教學設計與教學實施至少需遵循以下3個原則．

2.1 問題驅動原則

正如哈爾莫斯所言，問題是數學的心臟．問題也是數學課堂的核心，教學應依據歷史與學生實際對教材重組“再創造”，提出合適的真實問題，創設有效的教學情境驅動概念與原理的教學．教師為學生提供探索活動的適當問題空間，引導他們在“做數學”的過程中發現數學并習得相應的數學思想、學會思考，進而運用所學解決具體問題、鞏固新知、體驗“用數學”的過程．圍繞恰當問題情境展開教學，有助于培養學生發現問題與提出問題、分析問題與解決問題的能力．

2.2 密切聯系現實原則

這里的“現實”有兩層含義：一是指學生的數學基礎與實際生活經驗，二是數學產生的背景．問題驅動教學的關鍵是創設真實的問題并賦予有效的情境，教師進行教學的設計與組織時必須考慮學習主體——學生的現實，使提出的問題在學生思維的“最近發展區”，使依據數學產生背景所創設的教學情境是學生所能理解的現實情境、科學情境或數學情境．數學在解決各種各樣的問題中形成相應的概念和原理，教學應該創設適當的問題及其情境反映這個過程并讓學生體會到數學的廣泛應用性、深刻性、嚴謹性與趣味性．學生在問題情境中經歷從現實世界向數學世界和符號世界過渡的完整“數學化”過程，在獲得基本知識與技能、基本思想與活動經驗的同時學會“用數學的眼光觀察世界、用數學的思維思考世界、用數學的語言表達世界”[4]，促使數學學科核心素養的形成和發展．

2.3 知識生成原則

學生已有的知識儲備和相應的知識結構是學習新知識的重要支架．新知應在舊知的基礎上引發，學生在經歷知識的發生過程中建立起知識間的實質和意義聯系，進而形成良好的整體認知結構，促進學生對知識的理解并實現學習的遷移．這也要求教師深入到數學內部剖析教材內容，確定教學的困難或存在的問題，明確單元的整體知識結構以及各知識點在單元內部、單元之間、數學學科內部和外部之間的聯系，理清知識脈絡與所體現的主要數學思想，以尋找教學的合適生長點．

3 問題驅動數學教學的基本思想

有效實施問題驅動數學教學的前提是教師能依據歷史和學生實際重構教材，整體把握教學內容，確定核心問題，設置恰當的現實問題情境，在此基礎上引領學生經歷“數學化”的完整過程．數學具有“原始形態”“學術形態”“教育形態”3種存在形式[16]．教師應具備將知識在數學史中的“原始形態”和教科書中的“學術形態”轉化為再現知識發生發展過程的“教育形態”的能力．如果說，研究數學史和教科書是為了揭示數學知識的本質與教學價值，以厘清“教什么”與“為什么教”．那么將數學的“原始形態”和“學術形態”有效轉化為便于學生接受的“教育形態”，就是為了解決“如何教”的問題．因此，問題驅動數學教學的組織與實施需把握以下4個基本思想．

3.1 基于對教學單元的整體把握 深入理解具體課時內容

課時內容是單元的一個部分，單元則是數學學科結構中最小的整體．要掌握局部的課時內容，就需理解其在單元中的地位與作用．進一步地，還需了解單元與數學學科整體結構的聯系，甚至是與其它學科的聯系．這樣才能設置恰當的問題與情境更好地組織具體課時的教學．要整體把握數學單元，就是要依據課程與單元專題的總體目標、教材的體系、數學史和學生的實際去深入剖析教學內容的價值與地位．換句話說，把握數學知識的整體結構是為了服務局部的課時內容，為了更好地揭示知識背后的思想及相互間的聯系．而充滿各種聯系的局部內容構成了具有生命力的整體認知結構．

3.2 基于歷史與學生現實“再創造”教材內容 呈現知識的教育形態

數學專著的內容基本以學術形態呈現一堆數學化的形式結果，看不到知識的起源與發展，感受不到數學家曲折而豐富的思考過程．教科書雖然不同于數學專著，但為了便于組織也基本按照“定義→定理或公式法則的證明→應用”的順序組織教材．數學史則是以原始形態表現數學，反映知識的發生發展和思想方法的形成過程，但也包含了各種細節以及數學家所走過的彎路．弗賴登塔爾強調數學教學要經歷歷史上的重要步驟卻并非要重復歷史，而是要依據歷史結合學生的數學現實將數學的學術形態和原始形態轉化為適合學生學習的教育形態．所以，教師需整體把握數學學科知識，運用數學史知識和學生實際重構教材，圍繞問題在課堂教學組織中有的放矢地再現數學家“火熱的思考”過程，提升學生的數學素養．

3.3 基于問題驅動教學 揭示概念與原理的本質

數學概念特別是基礎的核心概念是數學這座大廈的基石，相應的理論和定理構成了大廈的框架，各個定理、命題之間的相互關系及其蘊含的思想方法則充實了框架結構，形成了有血有肉的整體．以問題驅動教學是生成概念和獲得原理的最佳途徑，學生在合適的問題空間中進行探索活動并體驗數學思想方法的形成過程．雖然在實際的數學課堂教學中，不可能每節課都圍繞著一個核心問題展開教學．但對于在數學知識體系中起著基礎作用的重要概念和定理，最適合也最需要以問題驅動的方式展開教學來揭示數學的本質．通過問題驅動教學，讓學生深刻體驗數學概念與原理背后所隱藏的思想方法，體驗到數學的價值、作用與魅力．

一般而言，對于新課——如概念、定理、性質或公式的講授，應盡可能地選擇恰當問題設置真實有效的情境展開教學，讓學生有機會親歷數學的再發現過程．而在圍繞一節課的核心問題驅動教學的過程中，為了幫助學生更好地開展探究活動，教師仍需要給合學生的實際設置一系列有啟發性的、有前后邏輯關系的問題鏈．如果把核心問題比作“大問題”，那么問題鏈就是為了大問題的解決而設置的一個個小臺階，讓不同學習能力的學生都有機會到達目標——解決大問題并揭示數學本質．為鞏固新知，讓學生深刻理解概念的內涵與外延、原理的適用范圍與限制條件等，同樣也要設置一系列反映概念本質屬性、原理實質的變式問題進行習題課的教學．可見，問題總是教學的中心，但“問題鏈”與本原性問題、派生性問題在教學中的意義及作用不盡相同．

3.4 基于“數學化”的方法組織教學內容 構建相互聯系的知識結構

將數學內容問題化，將問題情境化，并以問題驅動教學是為了更好地實現“數學化”．讓學生經歷“數學化”過程的實質也是要求教師用“數學化”的方法組織教學內容的過程．弗賴登塔爾指出要教充滿聯系的數學，才有利于學生理解、記憶與運用知識，才能形成數學的整體結構．學生經歷橫向數學化的過程將數學與外部現實聯系起來，經歷縱向數學化的過程則是在數學的內部建立起彼此間豐富的聯系．通過“數學化”，幫助學生將一個個概念、原理、公式、法則有機組織在一起形成完善的知識體系獲得對數學本質的理解，實現知識在數學學科內部及其與其它學科之間的密切聯系．

4 問題驅動數學教學的基本步驟

數學研究的起點可以是數學問題也可以是科學問題或現實問題，在解決問題的過程中抽象出數學的概念與原理，進而運用結論解決其它的數學問題、科學問題或現實問題．數學研究的過程也反映了數學教育的基本過程，如圖1[5]，從“數學到數學”與從“現實到數學”是數學教育的兩條基本主線．“數學化”的出發點指研究的起點是數學問題，“生活化”的出發點指研究的起點為科學問題或現實問題．不管是從數學本身出發還是從現實開始，研究所獲得的結論既可用以解決數學問題也可處理實際問題．

圖1 數學教育的基本過程

數學教學是對數學的“再創造”，是要引領學生經歷數學的再發現過程．如果數學來源于生活問題或科學問題，教學情境就盡可能與學生生活實際密切聯系，體現數學的生活價值或科學價值．強調數學知識與現實生活的聯系也是“淡化形式，注重實質”[17-18]的教學體現．如果知識產生于數學內部的發展需要，問題就應融于適當的數學情境，反映知識的數學價值．這或許與徐利治先生所說的“數學教育不必強調應用，可以完全從數學的角度進行數學教育”[19]有一定的相通之處．

圖1給出了數學教育的基本路線與框架．對于具體課時的中學數學教學，為便于教師的把握與操作，可根據數學教育的基本過程，構建出更具操作性的問題驅動課時教學的基本步驟，如圖2．課時教學組織過程經歷Ⅰ→Ⅱ→Ⅲ→Ⅳ的4個步驟．

教學的起點可以是蘊含數學問題的科學情境、現實情境，也可以就是反映知識本質的數學情境，不管是哪種起點形式都要經歷“數學化”的教學組織過程．而且教學的終點都指向應用，用獲得的數學概念或原理解決數學問題或者實際問題．問題驅動數學教學讓學生經歷從感性認識上升到理性認識的學習過程，經歷發現問題與提出問題、分析問題與解決問題的過程，經歷數學知識與思想方法的形成過程．學生在數學活動中激發了探究精神，增強了數學建模能力和思辨能力，提升了問題意識和應用意識，發展了數學核心素養．

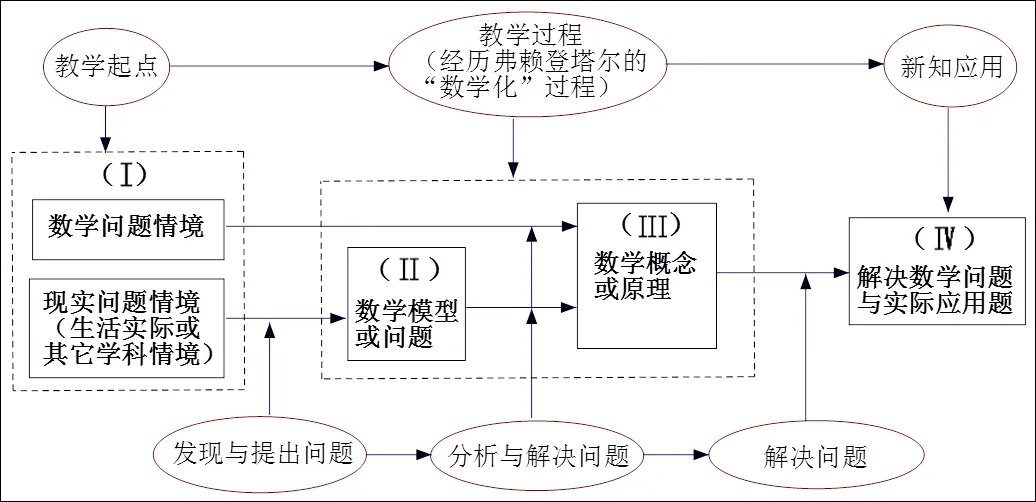
圖2 問題驅動數學課時教學的基本步驟

5 問題驅動數學教學的幾種形式

根據問題驅動數學課時教學的基本步驟，由于不同的問題情境，教學過程的展開也略有不同．

5.1 若促使數學知識產生的背景是來自現實或科學的本原性問題

此時教學過程基本按照圖2經歷從Ⅰ→Ⅱ→Ⅲ→Ⅳ的4個步驟，讓學生經歷從現實情境或科學情境抽象出數學模型或問題到解決問題獲得新知，再到應用新知的過程，學生同時經歷了“橫向數學化”與“縱向數學化”．比如“平面向量”單元“向量”概念的教學．向量本身就有極強的物理背景，自然可以通過分析學生所熟悉的既有大小又有方向的力（如重力、浮力、彈力等）后歸納抽象出向量的概念，從物理世界過渡到數學的符號世界，經歷橫向數學化．然后再深入探討向量的幾何表示方法、相等向量與共線向量的定義，在數學內部盡可能建立與向量的聯系，實現縱向數學化．再在解決問題中鞏固和運用向量的概念．

5.2 若促使數學知識的形成源于數學自身邏輯的本原性問題

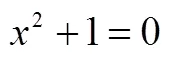
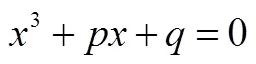
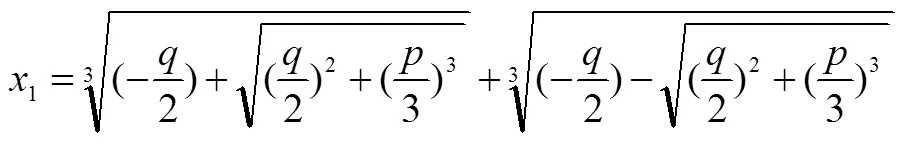
于是人們不得不考慮負數平方根的性質及其與實數的聯系，由此引入新數——虛數單位i和復數的概念．教學完全可以結合這樣的數學背景創設情境激起學生的認知沖突自然進入“縱向數學化”，然后從不同的角度理解和用不同的方式表征新知識，進而形成完善的概念并應用概念．

5.3 若數學知識的形成是源于數學內部形式邏輯推導的派生性問題

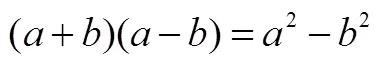
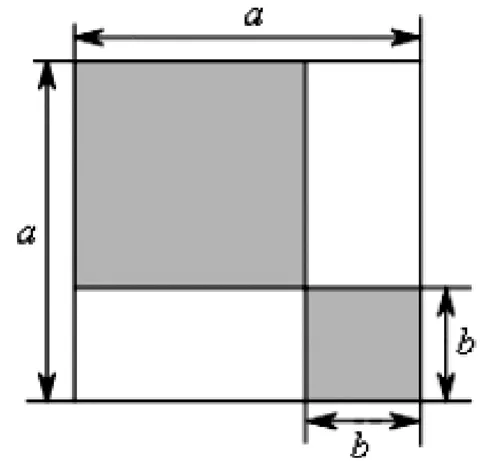
圖3 平方差公式的幾何解釋

[1] 鄧納姆．微積分的歷程——從牛頓到勒貝格[M]．李伯民，王軍，張懷勇，譯．北京：人民郵電出版社，2010：14．

[2] KLINE M. Calculus: An intuitive and physical approach [M]. New York: Dover Publications, Inc, 1998: 2.

[3] 高雪芬，汪曉勤．M·克萊因的HPM思想——以《微積分》為例[J]．數學教育學報，2012，21（4）：24-27．

[4] 中華人民共和國教育部．普通高中數學課程標準（2017年版）[M]．北京：人民教育出版社，2018：81-82，91-92．

[5] 曹廣福，張蜀青．問題驅動的中學數學課堂教學·理論與實踐卷[M]．北京：清華大學出版社，2018：7-8．

[6] 張奠宙，張蔭南．新概念：用問題驅動的數學教學[J]．高等數學研究，2004，7（3）：8-10．

[7] 李大潛．從數學建模到問題驅動的應用數學[J]．數學建模及其應用，2014，3（3）：1-9．

[8] 裴新寧．在“實習場”中“做科學”——問題驅動的科學探究學習環境設計[J]．全球教育展望，2001，30（1）：48-53．

[9] 曹廣福，張蜀青．論數學課堂教學與評價的核心要素——以高中導數概念課為例[J]．數學教育學報，2016，25（4）：17-20．

[10] 沈威，曹廣福．高中三角函數教育形態的重構[J]．數學教育學報，2017，26（6）：14-21．

[11] 盧建川．基于問題驅動的高中復數教學研究與教學內容的重構[D]．廣州：廣州大學，2016：25-95．

[12] 曹廣福，張蜀青，羅荔齡．問題驅動的中學數學課堂教學·概率與統計卷[M]．北京：清華大學出版社，2018：1-201．

[13] 曹廣福，盧建川，沈威．問題驅動的中學數學課堂教學·復數與三角卷[M]．北京：清華大學出版社，2019：1-160．

[14] 弗賴登塔爾．數學教育再探[M]．上海：上海教育出版社，1999：33-34．

[15] 鄭毓信．“問題意識”與數學教師的專業成長例[J]．數學教育學報，2017，26（5）：1-5，92．

[16] 李祎．高水平數學教學到底該教什么[J]．數學教育學報，2014，23（6）：31-35．

[17] 陳重穆，宋乃慶．淡化形式，注重實質[J]．數學教育學報，1993，2（2）：4-9．

[18] 陳重穆，宋乃慶．再談“淡化形式，注重實質”[J]．數學教育學報，1996，5（2）：15-18．

[19] 徐利治．談談我青少年學習數學的一些經歷和感想[J]．數學通報，2007，46（12）：1-5．

[20] 王海青．數學史視角下“數系的擴充和復數的概念”的教學思考[J]．數學通報，2017，56（4）：15-19．

The Fundamental Principles and Thoughts of Problem-Driven Mathematics Teaching and Its Implementation Steps

WANG Hai-qing1, CAO Guang-fu2

(1. School of Mathematics & Statistics, Huizhou University, Guangdong Huizhou 516007, China;2. School of Mathematics and Information Science, Guangzhou University, Guangdong Guangzhou 510006, China)

Problems is the original driving force for the development of disciplines, and mathematics is no exception. The problem-driven mathematics teaching research is based on the requirements of the curriculum standard “to create appropriate teaching situations and put forward appropriate mathematical problems”, and carry out corresponding theoretical thinking and practical exploration. The key to problem-driven mathematics teaching is to create real problems and explore them in effective situations. Teachers lead students to explore and generate mathematical knowledge in problem situations, acquire mathematical thinking methods and learn to think. Based on the problem-driven theory and the characteristics of mathematics, the basic principles and thoughts are analyzed, and the implementation steps of problem-driven mathematics teaching for specific classes are constructed to provide reference for teaching design and organization.

problem-driven; problem situations; mathematics teaching; mathematical thoughts

G632

A

1004–9894（2022）01–0024–04

王海青，曹廣福．問題驅動數學教學的基本原則與思想及其實施步驟[J]．數學教育學報，2022，31（1）：24-27．

2021–10–26

廣東省學校德育科研課題——基于“立德樹人”的高校課程育人途徑探索——以數學學科為例（2019GXSZ055）；廣東省教育研究院2019年教育研究課題——“U-G-S”協同機制下數學教師職前培養與職后培訓一體化建設研究；惠州學院自主創新能力提升計劃課題——整體主義視野下數學教師教學素養的提升研究（hzu201912）；惠州學院高等教育教學研究與改革課題——問題驅動教學的數學課堂研究（JG2018011）

王海青（1978—），女，廣東河源人，副教授，博士，主要從事數學史與數學教育研究．

[責任編校：周學智、陳雋]