怎樣促進學生提出和解決高價值的數學問題——等腰三角形單元教學對比實驗研究

吳增生，鄭燕紅，吳海燕，王澤峰

怎樣促進學生提出和解決高價值的數學問題——等腰三角形單元教學對比實驗研究

吳增生1，鄭燕紅2，吳海燕3，王澤峰4

（1．浙江省臺州市仙居縣教育教學研究中心，浙江 臺州 318000；2．浙江省臺州市仙居縣安洲中學，浙江 臺州 317300；3．浙江省臺州市仙居縣橫溪鎮新生中學，浙江 臺州 317312；4．浙江省臺州市天臺縣赤城中學，浙江 臺州 317200）

近幾十年來，對問題提出教學的研究卓有成效，問題提出與問題解決的認知關系、與數學與學生的學業成就關系、教學策略、教學模式等諸方面理論架構日趨成熟．但是教學實踐案例研究不夠廣泛和深入，特別是用數據說明教學效果的案例很少．研究以初中“等腰三角形”單元內容為例，提出了“用大觀念引領，基于單元整體教學設計，整合已有問題提出教學方法，促進學生提出和解決高價值的問題”的教學策略，在典型的城區學校和農村學校分別選擇樣本進行教學對比實驗，收集數據并用SPSS20.0軟件進行分析，并進一步進行效應量（ES）分析．結果表明，用這種教學策略能顯著提高促進學生提出并解決高質量的數學問題．

等腰三角形；問題提出和解決；教學對比實驗

1 研究背景

“提出問題”是科學研究中的一個重要環節，也是數學思考的開端．1989年，全美數學教師理事會（National Council of Teachers of Mathematics，簡稱NCTM）頒布的《學校數學課程與評價標準》提出“在數學教學中提供讓學生提出問題的機會”的主張，這標志著把“問題的提出”正式作為數學教育的問題來研究，引發了問題提出教學法研究的蓬勃發展．研究者從問題提出與問題解決的關系、問題提出與數學學業水平的關系、問題提出的認知策略、問題提出教學模式及實踐等方面展開研究，取得了豐富的成果．（1）問題提出與問題解決認知關系的研究．蔡金法等人進一步明確界定了問題提出教學的相關概念及不同表現形式，明確了問題提出與問題解決相融合的認知機制[1]．Christou、Mousoulides、Pittalis和Pitta-Pantazi（2005）通過考察職前教師用動態幾何軟件工具在平行四邊形研究中提出和解決問題能力的關系，發現這些職前教師在提出問題與解決問題活動中的認知表現符合蔡金法等人提出的上述理論框架．（2）問題提出與學生學業成就的研究．蔡金法等人研究發現，學生的問題提出活動可以發展學生的學業成就，反之，學生的高學業成就可以促進其提出好的數學問題（Cai和Hwang，2002；Cai等，2013），Silver（1997）研究發現問題提出促進學生的創造性思維能力，Kotsopoulos和Cordy（2009）等人以初中生為例，發現通過問題提出活動可以改進學生對數學知識的理解[1]．（3）問題提出的策略和方法研究．Kilpatrick（1987）提出了一些數學問題提出策略：觀念的聯結、類比、一般化、反駁、換位思維法和觀念組合法等，通過運用這些策略，可以幫助學生提出更多的好問題[2]；Silver（1994）提出了兩種提出問題的策略：一種是根據情境來提出問題，另一種是改編現有問題來提出新問題[3]；Moore-Russo和Weiss（2011）基于數學家決定后續研究方向的常用變式思考方式，以幾何內容為例，提出在已有問題基礎上提出新問題的5種策略[1]：強化/弱化條件，強化/弱化結論，一般化，特殊化，反向思考．（4）問題提出教學的研究．Contreras（2003）提出的PPM（Problem Posed Model）教學模式認為教師可以通過例題來講授提出問題的一般模式，激發學生提出問題[4]；Kontorovich等人在后續研究中（2012）就課堂上學生特定的集體活動情境，提出了解釋數學問題提出復雜性的綜合性理論框架：任務的組織、學生的知識基礎、問題提出的啟發式與圖式、小組工作的行為與互動模式及個體對適切性的考慮[5]．由Ellerton（2013）提出[6]、并經Xie（2017）[7]等進一步完善的主動學習框架（active learning framework），有助于在真實、復雜的數學教學環境中確定問題提出的位置和師生的角色及其變化．此外，經過Hildebrand（1999）[8]、Contreras（2007）[9]、GonzaLes（1998）[10]、Yeap（2009）[11]、Schloemer（1994）[12]等研究者的努力，在問題提出的教學目標和教學方案、師生角色定位、學習任務設計等諸方面取得豐富的成果．English（1997）在小學五年級5個班級中進行問題提出訓練實證研究，從五年級的150名學生中選出11位數感能力強而解決新穎問題弱的學生、4位數感能力弱而解決新穎問題強的學生以及12位兩者都強的學生（共27人）參與為期一年的提出問題系統訓練活動，通過前后訪談測評數據分析，發現進行問題提出訓練的學生在“創造新問題，發展新內容和拓展問題結構”3個指標上取得了較好的發展[13]．

Cifarelli和Cai（2005）提出的問題提出與問題解決認知循環理論，揭示了數學問題提出和問題解決的關系，在一般意義上為問題提出與問題解決融合教學提供了宏觀的認知活動框架．Silver給出了兩種提出問題的策略，明確了數學問題提出的基本分類和基本來源，為問題提出教學提供了可參照的方向．Moore-Russo和Weiss（2011）進一步細化了Silver的問題提出策略，提出了更具有操作性的問題提出方法，便于在教學中整合問題提出與解決活動，達成課程目標；Contreras、Kontorovich、Ellerton、Xie等人的教學模式研究，給出了可操作的教學設計和實施的方法，English（1997）的實證研究，為研究促進學生提出和解決問題能力的教學干預研究提供了有益的啟發．

在國內，數學問題提出教學研究始于20世紀90年代，2001—2003年快速發展，然后趨于平穩[14]．隨著課程改革的深入，“四基”“四能”要求出現在2011版義務教育課程標準及2017版普通高中數學課程標準中，又出現了快速發展的勢頭．呂傳漢、汪秉彝（2006）曾構建數學“情境—問題”的教學模式，給出了問題提出和解決的系統教學策略體系，建立了一個幫助教師設計提出問題情境的項目組，基于通常的課程，引領教師開發出了一系列的教學案例，在中國10個省市超過300所學校參與了該項目的培訓與研究[15]．蔡金法認為，問題提出教學研究中，對于用問題提出評估師生的數學思維，問題提出教學的理論框架，目前已經基本成型，目前缺的是具體的實踐來實現這些理念[16]．2019年，蔡金法帶領浙江蕭山的一批小學數學教師，開發了一批教學案例，發表于《小學數學教學》增刊上．此外，《數學教育學報》于2002—2003年集中發表了數學問題提出教學案例研究的論文．

已有研究表明，開展問題提出教學，能有效促進學生解決問題能力和創造性思維能力的發展（Cai和Hwang，2002；Cai等，2013；Silver，1997）；而且也有了促進學生提出問題的策略框架（如呂傳漢、汪秉彝提出的“情境—問題”策略，Silver提出的兩條策略，Moore-Russo和Weiss基于幾何內容的問題提出具體方法，English提出的發展學生問題提出和解決能力的訓練框架，等等）；通過訓練，教師和學生也有能力提出問題．但是，研究中也發現了學生提出的問題質量往往不高，往往會提出非數學、不可解和不相關的問題[17]．English（1997）提出的訓練問題提出和解決能力的策略框架是針對班級中的部分同學進行的，不能直接遷移到通常課程的課堂教學中，在國內已有的實踐研究中，至今很少發現基于數據分析的融合問題提出和解決教學實證研究，導致這些教學案例在改進學生學習、發展學生的問題提出和問題解決能力的效果方面說服力不足．

在許多案例中，教師把學生提出問題的數量作為首選目標，導致課堂滿堂問（細節性而繁多的變式問題），沒有幫助學生從宏觀上基于單元提出研究主題，沒有把問題提出與問題研究與解決很好地融合起來．如果說，小學階段可以通過變式提問實現學生對數學結構的多元理解，改進學習，到了初中高中，這種基于細節的繁多提問會干擾學生的學習．

開展問題提出和解決教學，首先要引導學生提出和解決高價值的數學問題．美國很多學者對提出的問題進行了不同的分類，雖然涉及到提出問題的流暢性、延展性、獨創性[18]，蔡金法給出了“不好”的問題3個現象——“非數學、不可解和不相關”，但是還沒有明確判斷問題好壞的一般標準．事實上，“不好的問題”反面，即“數學的、可解的、相關的”是“好”的問題的基礎，從數學學科本質上看，什么是“好”的問題？陳省身先生說過，一個好的數學家要知道什么叫好的數學，什么是不好或不太好的數學，有的數學是具有開創性的，有發展的，這就是好的數學；有些數學也蠻有意思，但漸漸變成游戲了[19]．這說明，“發展性”是數學好問題的核心特征．此外，學生的學習是基于課程內容的，需要達成課程目標的，“與課程內容及目標的契合性”也應該是好問題的主要特征之一（這里實際上把蔡金法提出的“相關性”特征進行了進一步的可操作性的細化描述）．因此，研究者將高價值的問題界定為具有“發展性，可解性，與課程內容及目標的契合性”3個特征的數學問題．問題的發展性指的是提出的問題具有創新性和內生性，能生成一系列新問題；問題的可解性指的是提出的問題在學生知識經驗范圍內是可解的；與課程內容及目標的契合性指的是，提出的問題反映數學的本質，反映相關課程的核心內容，有利于達成當前內容的課程目標．雖然創新性和情境性也是高價值問題的重要特征，但是在平時課堂中是體現在“發展性”中的．盡管依據課程內容進行的提出問題教學中，學生提出的是課本上的問題，但是對學生來說，如果是新穎的，這樣的問題也是他的拓展和創新，問題既可以從現實情境中發現和提出，也可以基于數學內在發展的邏輯來提出．

其次，開展問題提出和解決教學，還要有促進學生提出高價值數學問題的切實有效的教學策略和方法．學生提出問題需要經驗支撐，是具有領域特殊性的，需要基于具體內容的學習研究進行，從具體研究過程中形成“怎樣研究一類對象”的大觀念（Big Ides），引領學生有序地提出高價值的數學問題，這與Contreras（2003）提出的“通過例題講授提出問題的一般方法”觀點一脈相承，也與李懷軍、張維忠提出的“以學科大概念為中心選擇主題內容，創設情境，引導學生提出和解決問題”的觀點一致[20]．

數學問題提出，本質上是提出對事物的本質屬性、普遍聯系和一般規律的疑問，通過數學抽象實現數學化，引入研究對象，明確研究內容和研究目標，是對“在一定條件下能得到事物數量關系和空間形式的哪些屬性、關系和規律”的問題表述．在提出數學問題的過程中，需要對情境中對象及其關系進行數學結構化抽象和邏輯推理，這需要直觀想象、數學抽象、邏輯推理、數學運算、數學建模、數據分析等關鍵能力的支撐，它是數學學科核心素養的綜合體現；同時也是引發這些數學核心素養相關活動的起點．因此，開展提出問題和解決問題活動，對促進學生數學核心素養的發展，有著重要的作用．

研究者以等腰三角形內容為主題，用數學學科大觀念整合各種問題提出教學方法進行研究性單元整體教學設計，用下面3個策略引導學生提出并解決高價值的問題系列：（1）用學科大觀念引領，創設現實情境和數學情境引導學生通過類比和聯想提出主問題；（2）運用“類比，強化/弱化條件，強化/弱化結論，一般化，特殊化，反向思考”等策略引導學生從主問題中逐步分化出子問題系列，把總目標分解為一系列可達成的子目標，最終達成總目標，解決主問題；（3）通過對問題及其提出和解決過程的反思質疑和類比提出新問題，這與元認知相關．通過教學對比實驗，基于數據分析，考察這些教學策略能否促進學生提出和解決特殊三角形內容中新的高價值問題．

2 研究設計

2.1 概念界定

2.1.1 “問題提出”

要在具體內容中實施“問題提出”教學，明確“在教育意義上什么是問題提出”是基礎性的．在數學教育中，問題的提出指的是師生為了教學和學習目的而提出數學問題的活動，Cai和Hwang（2019）就數學問題提出從教師的角度和學生的角度做了全面的界定[21]，將“問題提出”定義為“師生基于特定情境（問題情境）形成（或再形成）和表達問題（或任務）的活動”，并將教師問題提出分解為5種特定的智力活動：（1）教師自己根據給定的情境提出數學問題；（2）教師預測學生根據給定的情境可能提出的問題種類；（3）教師通過改變現有的問題來提出問題；（4）教師為學生設定能夠提出問題的數學情境；（5）教師為學生提出可解決的數學問題．

2.1.2 幾何圖形研究的大觀念

研究表明，專家在解決問題時，具備了圍繞核心概念和原理的高度結構化的知識體系，而組織這種結構化知識體系的頂層組織結構、思想和觀念稱之為大觀念，這種大觀念有力地支撐了專家比新手具有更強大的提出問題和解決問題能力[22]．幾何大觀念指的是：融合空間視覺和用語言符號表達的邏輯推理研究幾何圖形的屬性及其關系，獲得對空間本質的理性認識．具體體現為：如何研究一類圖形及其關系的基本路徑、內容和思想方法，比如如何通過抽象獲得研究對象（從分析典型圖形的構成要素及其關系入手），概念的定義方式（名義定義、發生式定義、屬加種差定義等，它是確定圖形的充分必要條件），幾何圖形的性質指的是什么（確定圖形的必要條件——要素及相關要素各自及相互之間的穩定關系），判定是什么（確定圖形的充分條件——要素之間的關系），用什么路徑和方法（如抽象的思想、推理的思想、變換思想，定性研究與定量研究相結合的思想）研究等[23]．幾何圖形研究的一般觀念也體現在問題提出的層次性和系統性上：首先基于整體情境產生頂層目標，提出主問題；再根據研究思路逐步推進分化出指向總目標的子目標體系，從主問題出發提出層次清晰、指向主問題的子問題系列，通過總結、反思和質疑，提出新的、深層次的問題．

2.2 研究假設

在等腰三角形單元教學中，用幾何圖形研究大觀念引領，創設現實情境和數學情境引導學生通過類比聯想提出主問題；在圖形特例研究的一般思路和圖形變換思想引領下，運用“類比、強化/弱化條件、強化/弱化結論、一般化、特殊化、反向思考”等策略引導學生從主問題中逐步分化出子問題系列，并解決主問題；通過對問題及其提出和解決過程的反思質疑和類比提出新的研究問題．通過這樣的教學，可以有效促進學生提出和解決高價值的數學問題．

2.3 樣本與變量

選擇城區和農村有代表性的兩所初級中學作為實驗學校，城區學校是某縣城典型的大型普通初中，生源較好，農村學校是另一個縣的大型普通農村初中，學生水平中等．在城區初中選擇4個班級（共187人，其中男101人，女86人），兩個實驗班（95人，男49人，女46人），兩個控制班（91人，男52人，女40人）；農村初中選擇兩個班級共130人（男73人，女55人），一個班級為實驗班（67人，男40人，女27人），另一個班級為控制班（63人，男33人，女30人），共選取樣本317人．前兩章（三角形和全等三角形）章測試成績都沒有顯著性差異（>0.05）．實驗班和控制班由同一位教師執教（教齡10年以上的優秀教師），教學實驗前對實驗教師進行為期1天的培訓，實驗過程通過互聯網進行伴隨指導．通過這些措施，控制學生學業成績基礎變量和教師專業水平變量對教學效果的影響．著重分析實施這些教學策略對學生提出和解決高價值數學問題水平的影響．

2.4 教學對比實驗

2.4.1 教學的內容

教學內容是人民教育出版社課程標準教科書（2012版）第13章第三單元“等腰三角形”．

2.4.2 控制班教學方案

控制班根據教材的規定進行常規教學．進行基于知識點的講解式教學，第一課時為等腰三角形的性質，第二課時為等腰三角形的判定，學習知識點，講解例題，進行配套練習和作業，習題課1課時，共3課時．

2.4.3 實驗班教學方案

采用前文提出的教學策略進行單元整體教學．回顧與復習1課時，等腰三角形整體研究1課時，習題課1課時，共3課時．設計數學內在發展的邏輯情境和現實情境，基于三角形研究的路徑、內容和方法引導學生類比直角三角形提出“研究等腰三角形”這一主問題．教師再依據幾何圖形研究的大觀念引導學生規劃研究路徑，根據研究路徑分化出子目標，提出子問題系列，逐步解決主問題．然后，反思和總結問題解決的思想與方法，形成經驗，對問題提出和解決過程進行整體評價質疑，提出新問題．基于已有問題提出新問題的過程中采用Moore-Russo和Weiss的基于已有問題提出新問題的策略，通過類比、圖形的特殊化和一般化、反向思考（從性質定理的逆命題出發提出判定的問題）等方法提出子問題系列，通過這些子問題的解決最終系統地解決主問題：“怎樣研究等腰三角形？能得到哪些研究結論？”在解決了這一主問題后，基于研究過程的反思和總結，可以進一步提出等邊三角形和等腰直角三角形（通過特殊化）、含有30°角的直角三角形（通過分割和類比）及不等邊三角形（通過一般化）等研究問題．這些將作為評估學生提出和解決高價值問題能力問卷調查中的主要任務．等腰三角形的研究思路如圖1所示，教學過程中問題提出過程如圖2表示．

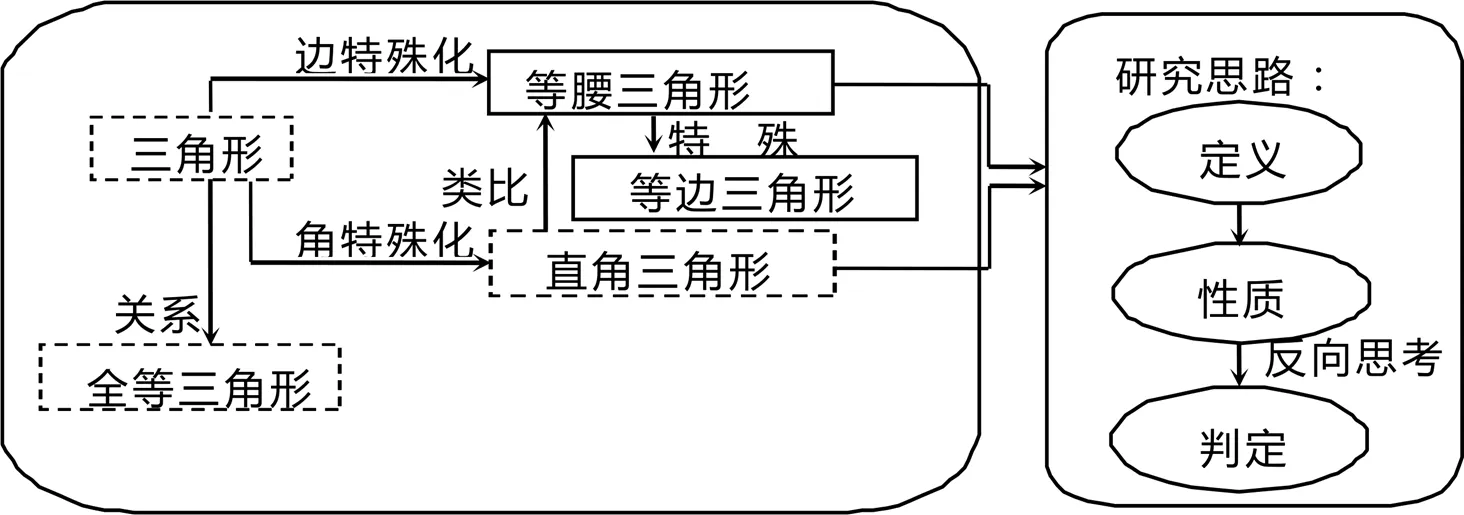
圖1 等腰三角形研究思路

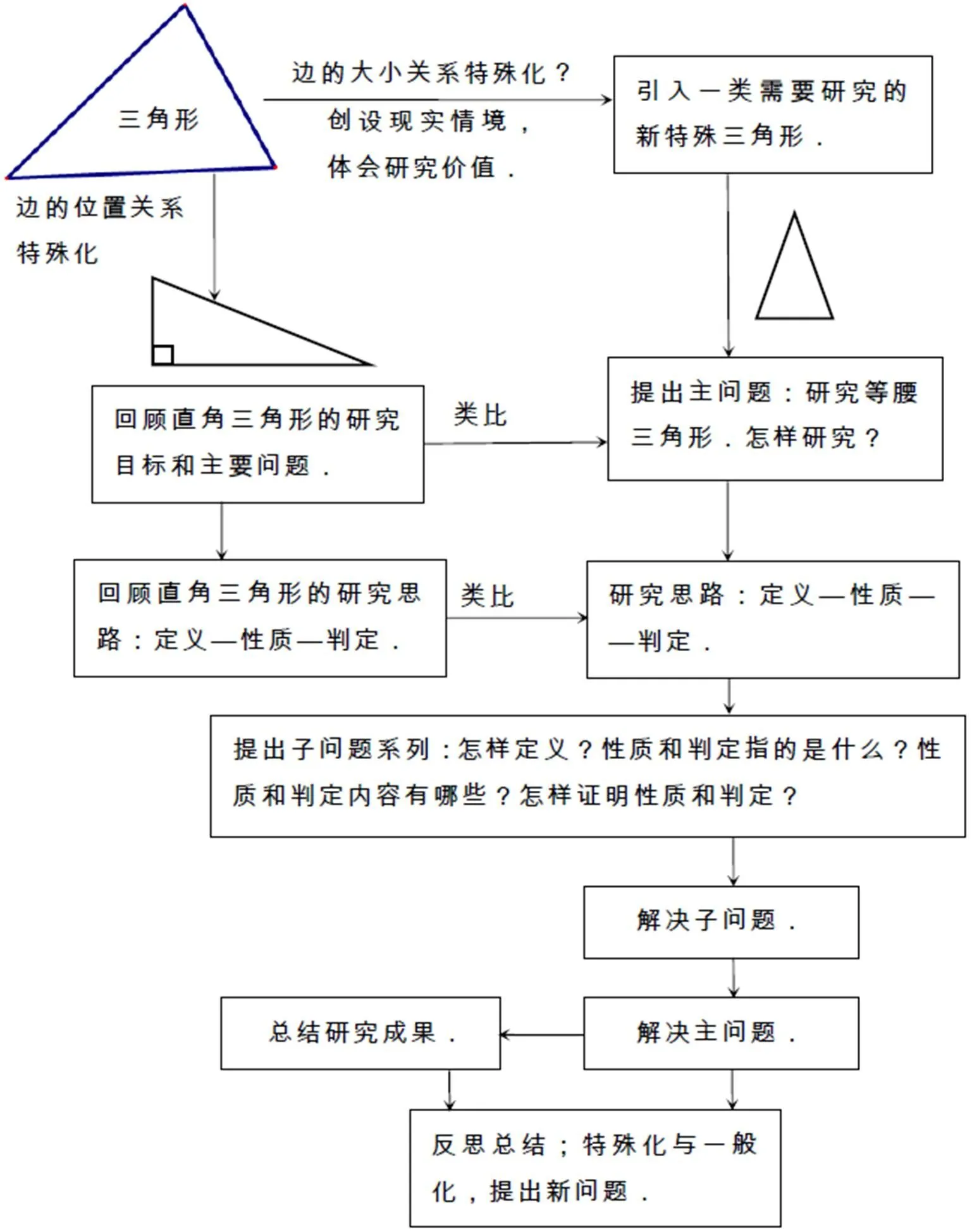
圖2 等腰三角形教學中問題提出和解決活動過程

2.4.3 實驗班教學過程

*預備教學

總結“三角形”“全等三角形”兩章內容的學習經驗，比如：如何引入研究對象（從現實情境中引入三角形和全等三角形）；從哪些角度定義三角形和全等三角形的（從三角形的邊、角基本元素關系角度給出充分必要條件）；從哪些角度研究性質（從三角形的邊、角這些基本元素和中線、高線和角平分線等相關元素的關系角度探索其不變性）；怎樣研究三角形全等的判定條件（從三角形的基本元素和相關元素關系出發，尋找能判定三角形全等的充分條件）；按照什么路徑研究三角形的：給出定義—研究性質—研究關系—研究特例（教科書中安排了對直角三角形兩銳角關系的研究，研究的路徑是：給出定義—研究性質—研究判定）．設計這一預備學習活動的目的是通過復習回顧形成“研究一類幾何圖形”的數學活動經驗，形成幾何圖形研究的大觀念．

*實施正式教學活動

（1）提出主問題．教師創設數學情境和現實情境，運用適當的指導語引導學生引入等腰三角形，提出主問題：研究等腰三角形的空間結構特征．

教師：前面我們在研究三角形的基本性質中，研究了直角三角形這種幾何圖形，你認為它是由一般的三角形怎樣特殊化得到的？類似地，你能提出需要研究的、新的、特殊的三角形嗎？

學生：

問題1：研究有一個角為60°的三角形（三角形內角的特殊化）；

問題2：研究有一個角為45°的三角形（三角形內角的特殊化）；

問題3：研究兩邊相等的三角形（三角形邊的大小關系的特殊化）；

……

教師評價啟發：在提出的特殊三角形中，兩邊相等的三角形在現實中出現得比較多（展示生活中等腰三角形形象的圖片），因此，首先來研究等腰三角形．

設計意圖：創設數學和現實情境，在圖形特例研究大觀念引領下，通過特殊化和類比引入研究對象．

（2）明確研究目標．教師運用適當的指導語引導學生分析主問題中的研究對象的構成（或決定）要素和相關要素，提出從哪些方面研究主問題．

教師：要研究等腰三角形，你覺得要研究哪些內容？可以類比前面直角三角形和全等三角形來提出要研究的問題．

學生：

問題1 什么是等腰三角形，等腰三角形有哪些性質？怎樣判定？

師生活動：教師引導學生回顧等腰三角形的定義，介紹頂角、腰、底邊等概念．并進一步提出研究等腰三角形性質和判定問題．

問題2 研究等腰三角形的性質，性質指的是什么？

問題3 研究等腰三角形的判定，判定指的是什么？

教師評價總結：對于一類幾何圖形，明確定義、研究基本性質和判定，是研究的基本內容．主要從邊、角等基本要素以及中線、高線和角平分線等相關要素研究．

設計意圖：通過等腰三角形的要素分析，明確研究內容和目標，提出研究的主問題．

（3）規劃研究路徑．教師通過指導語引導學生規劃研究的思路和基本方向．

教師：要用推理的方法研究等腰三角形的性質和判定，類比直角三角形，你能從研究方案的角度提出哪些問題？

學生：

問題1 從哪里出發研究性質和判定？——從定義出發，即從“三角形的兩邊相等”這個條件出發．

問題2 研究的思路是什么？定義—性質—判定．

教師評價啟發：下面，從定義出發，從邊、角等基本要素和中線、高線、角平分線等角度研究它們各自的關系，得到三角形的性質．

設計意圖：通過類比提出怎樣研究的問題，規劃研究的思路．

（4）建構等腰三角形性質研究的子問題系統．教師通過指導語引導學生提出性質研究的子問題并加以解決．

教師：從等腰三角形的兩邊相等這一條件出發，要研究性質，你能提出哪些問題？

學生：

問題1 邊有什么性質？

教師評價：這是定義．那么，除此以外還能提出哪些研究問題？

學生：

問題2 角有什么性質？

問題3 中線、高線、內角平分線有什么性質？

教師評價啟發：大家能提出這些性質的猜想嗎？是怎樣發現這些性質的？

學生活動：

用測量、觀察和對折實驗的方法發現性質：等腰三角形的兩底角相等，頂角的平分線、底邊上的中線和高線重合，兩腰上的中線、高線及兩底角的平分線長相等，等等．

教師引導學生進一步通過質疑直觀發現的可靠性，提出問題4：為了確定猜想是否正確，需要證明．怎樣證明這些猜想？

引導學生進行一步提出派生性問題：

證明幾何命題的步驟有哪些？已知條件是什么？結論是什么？

學生活動：獨立地證明猜想，寫出已知、求證和證明，進行證明過程的交流和質疑，并進一步證明等腰三角形的軸對稱性，理解等腰三角形的性質是它的軸對稱性在它的構成要素、相關要素上的反映．

設計意圖：在圖形研究的大觀念引領下，理解圖形的性質指的是什么，提出性質的研究問題；通過直觀觀察、想象、歸納的方法提出性質猜想，通過演繹推理證明猜想，得到性質．從而解決性質研究的主問題．

（5）構建等腰三角形判定研究的子問題系統．教師引導學生類比直角三角形研究，依據研究思路，提出等腰三角形判定的子問題，并逐一加以解決．

教師：研究等腰三角形的判定，要解決哪些問題？

學生：

問題1 什么是等腰三角形的判定？滿足什么條件的三角形是等腰三角形？

問題2 可以從哪些方面提出等腰三角形的判定？

問題3 可能有哪些判定？

教師啟發：能從三角形的構成要素和相關要素出發，找到可以判定三角形兩邊相等的最少條件嗎（從角的關系找，從中線、高線和內角平分線關系找）？

學生活動：通過類比直角三角形的研究，指出從角、中線、高線、角平分線角度通過考察性質定理的逆命題提出判定猜想：有兩個角相等的三角形是等腰三角形；一邊上的中線、高線和其對角平分線中有兩條重合的三角形是等腰三角形（學生可能提出“三線合一”條件，教師引導減少條件得到這個猜想）．

教師啟發：先從等腰三角形的基本要素邊和角的角度研究其判定，在得到等腰三角形判定的猜想后還需要做什么？

學生活動：獨立證明提出的判定猜想，畫出圖形，寫出已知、求證及證明過程，進行交流與質疑．

教師啟發：現在來研究從三角形的相關元素關系出發研究等腰三角形的判定．

學生活動：學生分組研究，提出猜想，給出證明．

設計意圖：在圖形研究的大觀念引領下，理解圖形特例的判定指的是什么，提出判定的研究問題；通過對性質定理的逆向思考，從考察其逆命題中提出判定的猜想．并通過演繹推理證明猜想，解決判定研究的子問題．

（5）引導學生反思總結．教師在等腰三角形的定義、性質、判定等探究環節結束后，引導學生及時地進行反思總結．

定義環節總結：

教師：得到了等腰三角形的定義，能總結一下是怎么得到的嗎？

學生：類比直角三角形定義，從邊的大小關系的特殊化得到的．

性質研究環節總結：

教師：等腰三角形的性質的條件和結論分別是什么？能總結你的研究過程嗎？從哪些方面總結？

學生：等腰三角形性質的條件是“兩邊相等”，結論是“這兩邊所對的內角相等，底邊上的高線、中線和頂角平分線重合”，這些性質是等腰三角形的軸對稱性在等腰三角形的構成要素和相關要素上的反映，是通過觀察、歸納提出猜想，再證明的方法研究的．

判定環節總結：

教師：等腰三角形判定的條件和結論分別是什么？能總結你的研究過程嗎？從哪些方面總結？你能總結等腰三角形的研究思路、研究內容和研究方法嗎？

學生：

等腰三角形判定的條件是“兩個角相等”結論是“等角所對的邊相等”；條件是“一邊上的中線、高線與它的對角的平分線中有兩條重合”結論是“其余兩邊相等”．

等腰三角形的研究思路是：定義—性質—判定．

等腰三角形的研究內容是：性質和判定；從邊、角和“三線”角度考慮．

研究方法是：通過直觀觀察和歸納發現結論，提出猜想，證明猜想；交換性質定理的條件與結論位置，提出判定猜想．一般到特殊的思想，軸對稱變換思想、類比的思想．

在等腰三角形研究整體完成后，引導學生總結研究過程及知識結構如圖3．

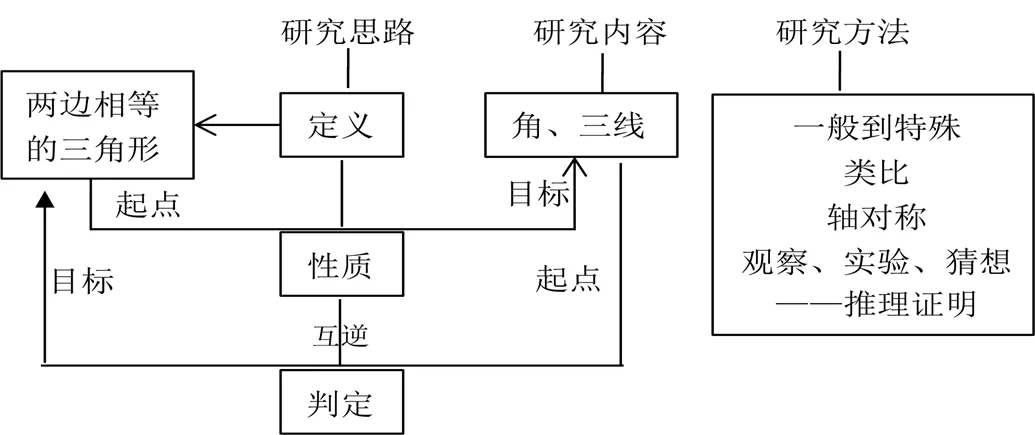
圖3 等腰三角形研究活動總結

設計意圖：通過分階段的反思總結，進一步提煉圖形特例的研究思路、研究內容、研究方法，發展學生的元認知，為后繼學習提供可遷移的問題提出和解決活動經驗．

2.5 數據分析方法

2.5.1 設計前后測訪談題目

為了檢驗這種教學方法能否促進學生在特殊三角形研究領域提出和解決高價值的問題，設計教學前后的兩次書面訪談任務作為評價工具．在等腰三角形內容教學前，安排一次前置性訪談I，在等腰三角形內容教學后，安排教學后訪談Ⅱ．兩次訪談時間均為60分鐘．

訪談I：類比直角三角形，你能通過特殊化提出新的特殊三角形進行研究嗎？請你把三角形特殊化后得到盡可能多的新三角形，提出研究問題，選擇一類特殊的三角形進行研究，寫出研究報告．

訪談Ⅱ：類比直角三角形和等腰三角形，你能發現新的特殊三角形嗎？請寫出盡可能多的新三角形，畫出圖形，提出研究問題，選擇一類特殊三角形進行研究，寫出研究報告．

2.5.2 訪談結果的數字化編碼方案

收集學生提出的問題及其解決過程，進行數字化編碼（方案事前由研究者設計，編碼由非實驗教師實施），在數字化編碼的基礎上，用SPSS20.0分析前后訪談的相關性和均值差異．

提出問題成績從提出問題的數量和質量兩方面進行賦分編碼，編碼的具體方案為：根據提出符合前文提出的高價值特征的問題數量，每個問題記1分，提出有創新性的主問題每個問題加1分．如在訪談I中提出含45o角的直角三角形研究問題，含有30o的直角三角形等研究問題，含有60o角的直角三角形研究問題，都計1分．如果提出含有50o角的直角三角形，由于在學生認知水平上不可解，則不得分．如果是提出兩銳角互余的三角形研究問題，由于實質上是直角三角形研究問題，缺乏發展性，則不得分．如果提出等腰三角形、等邊三角形、不等邊三角形等問題，因為從新的特殊化角度提出問題，具有創新性和發展性，每個問題記2分．在訪談Ⅱ中，如果提出等邊三角形的研究問題得1分，提出等腰直角三角形（或含有45o角的直角三角形）研究問題得2分（因為同時考慮了邊的特殊化和角的特殊化），提出含有30o的等腰三角形得1分，如果提出不等邊三角形的研究問題得2分，等等．由于提出問題訪談具有開放性，采用按照學生實際提出問題的數量和質量編碼方法，不設總分限制．

解決問題的成績包含定義、性質、判定的數學表達的全面性、準確性，以及推理過程的邏輯性．具體編碼方案為：定義0～2分，定義準確2分，基本準確1分，不準確0分；性質0～4分，準確描述性質2分，不夠準確1分，不相關0分，證明過程按照嚴謹性給0～2分；判定0～4分，準確表述2分，不夠準確1分，不相關0分，證明過程根據其嚴謹性給0～2分；提出與教科書不一樣的性質和判定加1分，能給出正確證明的，再加3分．滿分14分．

2.5.3 數據分析方法

首先用SPSS20.0進行相關檢驗，分析317位學生的前后測成績相關性，問題提出的前后測及問題解決的前后測均在0.01水平上顯著相關，具有較好的信度．在此基礎上，采用SPSS20.0對實驗樣本和控制樣本的問題提出成績增量和問題解決成績增量的均值進行獨立樣本檢驗分析，并在此基礎上進一步計算效應量值（ES Cohen’s），

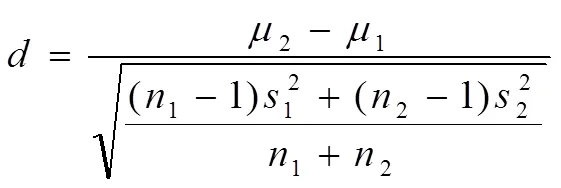
分析實驗樣本與控制樣本在提出和解決問題成績增量之間差異，其中的值為0.2以上，0.5以上，0.8以上分別對應著小、中、大的效應．

3 研究結果

用SPSS20.0分析城區學校及農村學校的前測成績，發現問題提出與問題解決成績均沒有顯著性差異（>0.1）.再計算問題提出和問題解決的成績增量（后測成績—前測成績），用SPSS20.0進行獨立樣本檢驗，城區組結果如表1、表2，農村組結果如表3、表4．

表1 城區學校成績增量組統計量

表2 城區學校成績增量獨立樣本檢驗

表3 農村學校成績增量組統計量

表4 農村學校成績增量獨立樣本檢驗

由表1、表2可知，城區學校中，實驗樣本的在特殊三角形研究領域中問題提出和問題解決成績提升增量顯著地好于控制樣本（<0.05）．由表3、表4可知，在農村學校，實驗樣本的在特殊三角形研究領域中問題提出和問題解決成績提升增量顯著地好于控制樣本（<0.05）．

進一步計算Cohen’s進行效應量（）檢驗，問題提出的增量值和問題解決的增量值Cohen’s計算結果如表5、表6．

問題提出增量中，城區實驗樣本與控制樣本的值為0.56，說明這些教學策略取得中效果，農村實驗樣本和控制樣本值0.81，說明這些教學策略取得大效果．問題解決增量中，城區實驗樣本與城區控制樣本值為0.65，農村實驗樣本與農村控制樣本的值為0.54，說明這些教學策略取得中效果．

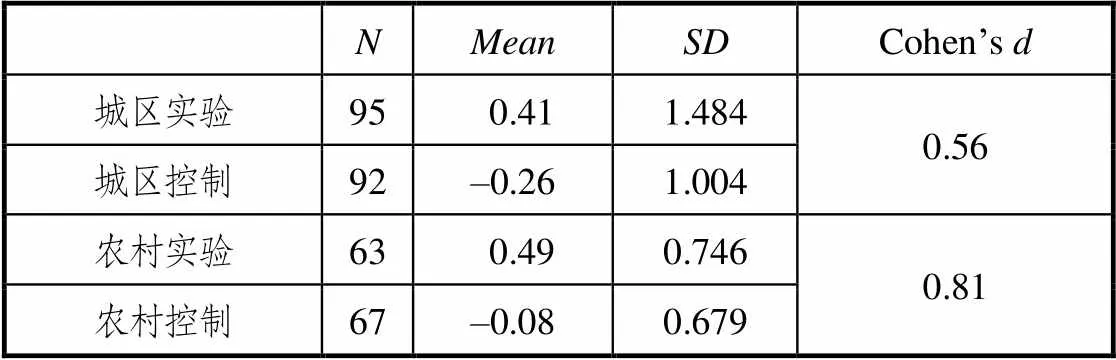
表5 問題提出增量Cohen’s d計算

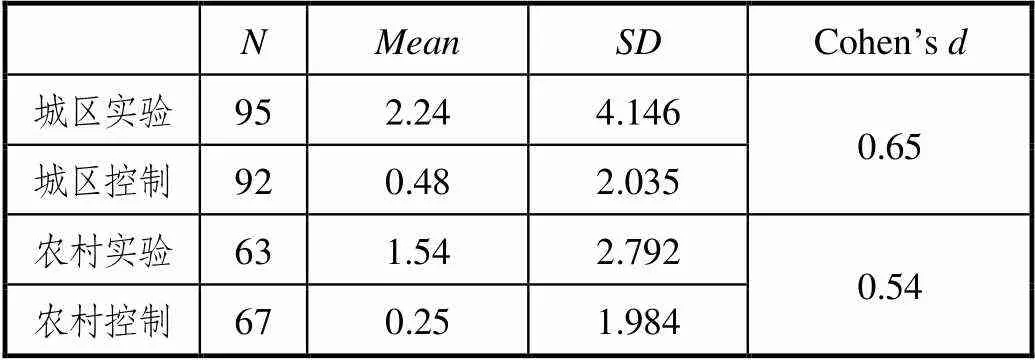
表6 問題解決增量Cohen’s d計算

4 研究結果的討論

上述數據分析顯示，通過研究提出的問題提出和解決教學策略組織教學，可以顯著促進學生提出和解決有價值的問題．產生這種效應的原因如下．

第一，根據Cifarelli和Cai（2005）的問題提出和問題解決認知循環發展理論設計問題提出和問題解決相融合的教學宏觀結構，讓學生完整經歷了問題的發現、提出、分析和解決過程，可以幫助學生更深刻地理解問題提出與問題解決的關系，學會從反思和總結已有問題提出和解決過程中總結經驗，有利于提出和解決新的有價值的問題．通過給學生創造提出問題和解決問題的機會，讓學生在問題提出和解決實踐中形成問題意識，形成問題提出和解決的活動經驗．

第二，在等腰三角形的教學過程中，讓學生完整地經歷等腰三角形的性質、判定的研究過程，基于幾何圖形的直觀想象進行概念的形成、性質和判定的語言概括并通過邏輯推理建立知識結構的過程，這符合幾何推理能力發展基于視覺空間與語言符號推理相結合的認知原理【Duval（2017）[24]，Tall D，等（2012）[25]】，可以比較有效地提高學生的幾何推理能力，支撐了等腰三角形研究中幾何問題解決活動．

第三，在等腰三角形的研究中，引導學生通過類比提出新的研究問題，發展等腰三角形的知識內容，通過子問題系列細化等腰三角形研究，形成有序分級的問題系統，這符合English（1997）提出的發展學生“創造新問題，發展新內容和拓展問題結構”能力的提出和解決問題能力的訓練框架，有利于學生提出和解決問題能力的發展．

第四，對三角形與全等三角形的回顧與復習是用幾何圖形研究的大觀念指導的，這種大觀念可以讓學生領會組織幾何知識及問題提出和解決的“幾何直觀和語言符號表達的邏輯推理相結合”的頂層觀念，引導學生從研究對象的引入和定義、研究思路的規劃、研究內容的確定、研究方法的總結等諸方面對已有的三角形及直角三角形研究過程進行整體回顧和整理，獲得一類幾何圖形及其特例研究的大觀念，這種通過復習活動獲得的幾何特殊圖形研究大觀念，為學生引入新的特殊三角形，提出主問題，提出和解決子問題，最終解決主問題提供了思考的方向標和導航框架．

第五，等腰三角形研究主問題提出過程中，實際上以從一般三角形到直角三角形的特殊化為參照，采用了Kilpatrick（1987）提出的類比策略及Moore-Russo和Weiss （2011）提出的基于已有問題提出新問題的特殊化變式提問方法，類比直角三角形進行，這也為在等腰三角形研究經驗基礎上通過特殊化引入新的特殊三角形，提出新問題提供了經驗支撐．

正是由于上述原因，實驗班學生能提出新的一類特殊三角形的研究問題，在幾何特殊圖形研究的大觀念引領下，進行系統的研究，解決新問題，寫出研究報告．由于控制班采用了基于知識點的碎片化教學，沒有提供提出問題、進行系統研究并最終解決問題等活動機會，也沒有幾何特殊圖形研究大觀念的指導，導致學生在面對“沒有具體題目”情境時，束手無策，不知道朝著什么方向思考．

5 研究的意義和局限

5.1 研究的意義

首先，研究根據問題提出教學的相關理論，通過教學實踐再次驗證了Cifarelli和Cai的問題提出和解決交替融合策略的可行性和有效性及Kilpatrick、Silver、Moore-Russo和Weiss、English等人提出的問題提出教學策略的有效性．

其次，研究提出了用幾何圖形研究的大觀念作為學生提出和解決問題的方向標和導航框架，基于單元內容進行教學整體設計，綜合運用各種促進學生提出問題的策略和方法，為學生提出和解決高價值的問題提供了方法論上的支撐，能有效促進學生在反思總結的基礎上通過類比和特殊化進一步提出新的特殊三角形的研究問題，并能進行系統研究．這是研究的創新點，也可以作為問題提出和解決的新策略應用在今后在課堂中，引導學生提出高價值的問題并加以系統研究與解決．

研究提出的“高價值數學問題”的特征是“發展性、可解性、與數學內容及其學習目標的契合性”，這一觀點可以為判斷教師和學生提出問題的價值提供一種參照．

最后，研究為等腰三角形內容的問題提出教學提供了一個典型的教學案例，而且這一案例的教學效果具有實證數據的證據支撐．

5.2 局限和展望

雖然研究者考慮到了中國的城鄉學校二元差異，分別從城區和農村選擇了有代表性的初中學校，對317名學生，6個班級（城區4個班級，農村2個班級）進行教學對比實驗，但研究過程并沒不包括農村偏遠學校，今后需要進一步研究偏遠地區學校是否適合這種問題提出教學；其次，總體上學生提出問題的水平還不夠高，可能需要長期堅持這種教學方法才能產生更好的總體效果；第三，大觀念對數學問題的提出起到了很好的導航作用，但這種專家具有的一般觀念是分領域的，今后需要根據不同的內容進行分別研究并進行教學實踐驗證；第四，研究通過綜合應用問題提出的相關理論和幾何圖形研究的大觀念進行問題提出教學研究，影響教學效果的因素可能既有給學生提供問題提出和解決機會的作用，同時還有數學大觀念的引領作用，今后需要深入研究這些要素各起到什么作用.

6 研究結論

研究表明，以等腰三角形單元內容為主題，用“怎樣研究一類幾何圖形”的大觀念為引領，采用單元整體教學，綜合應用Cifarelli和Cai的問題提出和解決交替融合策略，Kilpatrick、Silver、Moore-Russo和Weiss、English等人提出的提出問題教學策略，能顯著提高學生提出和解決高價值的數學問題的能力．這些教學策略在等腰三角形內容中可以進一步具體化為：用幾何圖形特例研究大觀念引領，創設現實情境和數學情境引導學生通過類比聯想提出主問題；在圖形特例研究整體思路和圖形變換思想引領下，運用“類比、強化/弱化條件、強化/弱化結論、一般化、特殊化、反向思考”等策略引導學生從主問題中逐步分化出子問題系列，分步解決子問題，最終解決主問題；通過對問題解決過程的反思質疑和類比提出新的研究問題．

研究不僅為這些已有的教學策略的有效性提供了有確定證據的教學實踐案例闡釋，而且，首次提出了“用數學大觀念整合各種問題提出教學方法進行研究性單元整體教學”教學設計思想，給出了3個具體的教學策略，并通過教學對比實驗檢驗其有效性．這為問題提出教學方法應用于課堂教學實踐，提供了一條可行的新技術路線．

[1] CAI J, HWANG S, JIANG C, et al. Problem-posing research in mathematics education: Some answered and unanswered questions [M]. New York: Springer, 2015: 3–34.

[2] KILPATRICK J. Problem formulating: Where do good problems come from [M] // SCHOENFELD A H. Cognitive science and mathematics education. Hillsdale: Lawrence Erlbaum Associates, 1987: 123–147.

[3] SILVER E A. On mathematical problem posing [J]. For the Learning of Mathematics, 1994, 14 (1): 19–28.

[4] CONTRERAS J N. A problem-posing approach to specializing, generalizing, and extending problems with interactive geometry software [J]. The Mathematics Teacher, 2003, 96 (4): 270–275.

[5] KONTOROVICH I, KOICHU B, LEIKIN R, et al. An exploratory framework for handling the complexity of mathematical problem posing in small groups [J]. The Journal of Mathematical Behavior, 2012, 31 (1): 149–161.

[6] ELLERTON N F. Engaging pre-service middle-school teacher-education students in mathematical problem posing: development of an active learning framework [J]. Educational Studies in Mathematics, 2013, 83 (1): 87–101.

[7] XIE J, MASINGILA J O. Examining interactions between problem posing and problem solving with prospective primary teachers: A case of using fractions [J]. Educational Studies in Mathematics, 2017, 96 (1): 101–118.

[8] HILDEBRAND C, LUDEMAN C J, MULLIN J. Integrating mathematics with problem solving using the mathematician’s chair [J]. Teaching Children Mathematics, 1999, 5 (7): 434–442.

[9] CONTRERAS J. Unraveling the mystery of the origin of mathematical problems: Using a problem-posing framework with prospective mathematics teachers [J]. The Mathematics Educator, 2007, 17 (2): 15–23.

[10] GONZALES N A. Problem posing: A neglected component in mathematics courses for prospective elementary and middle school teachers [J]. School Science and Mathematics, 1994, 94 (2): 78–84.

[11] HAR Y B. Mathematical problem posing in Singapore primary schools [M] // KAUR B, YEAP B H, KAPUR M. Mathematical problem solving: Yearbook 2009, association of mathematics educators. World Scientific, 2009: 102–116.

[12] SCHLOEMER C G. Integrating problem posing into instruction in advanced algebra: Feasibility and outcomes (Doctoral dissertation) [Z]. Retrieved from ProQuest Dissertations and Theses. (UMI No. 741899141), 1994.

[13] ENGLISH L D. The development of fifth-grade children’s problem-posing abilities [J]. Educational studies in Mathematics, 1997, 34 (3): 183–217.

[14] 尚亞明，何憶捷，熊斌．中國數學問題提出研究的回顧與展望[J]．數學教育學報，2019，28（6）：81–86．

[15] 呂傳漢，汪秉彝．論中小學“數學情境與提出問題”的教學[J]．數學教育學報，2006，15（2）：74–79．

[16] 蔡金法，姚一玲．數學“問題提出”教學的理論基礎和實踐研究[J]．數學教育學報，2019，28（4）：42–46．

[17] CAI J, HWANG S. Generalized and generative thinking in US and Chinese students’ mathematical problem solving and problem posing [J]. The Journal of Mathematical Behavior, 2002, 21 (4): 401–421.

[18] 于文華．美國數學問題提出：是非與評述[J]．數學教育學報，2018，27（2）：24–28．

[19] 國際數學大師陳省身談二十一世紀的數學[J]．高等數學研究，2001，4（2）：2–5．

[20] 李懷軍，張維忠．國外“數學問題提出教學法”研究：回顧與前瞻[J]．浙江師范大學學報（自然科學版），2020（1）：108–114．

[21] CAI J, HWANG S. Learning to teach through mathematical problem posing: Theoretical considerations, methodology, and directions for future research [J]. International Journal of Educational Research, 2020 (102):101–391.

[22] NIEMI D, VALLONE J, VENDLINSKI T. The power of big ideas in mathematics education: Development and pilot testing of POWERSOURCE assessments. CSE Report 697 [Z]. National Center for Research on Evaluation, Standards, and Student Testing (CRESST), 2006.

[23] 章建躍．研究三角形的數學思維方式[J]．數學通報，2019，58（4）：1–10．

[24] DUVAL R. Understanding the mathematical way of thinking: The registers of semiotic representations [M]. Springer International Publishing, 2017: 1.

[25] TALL D, YEVDOKIMOV O, KOICHU B, et al. Cognitive development of proof [M] // HANNA G, de VILLIERS M. Proof and proving in mathematics education. Springer, Dordrecht, 2012: 13–49.

How to Promote Students to Pose and Solve High-Value Mathematical Problems——A Comparative Experimental Study on Isosceles Triangle Unit Teaching

WU Zeng-sheng1, ZHENGYan-hong2, WU Hai-yan3, WANG Ze-feng4

(1. Education and Teaching Research Center of Xianju County, Zhejiang Taizhou 318000, China;2. Anzhou Middle School, Xianju County, Zhejiang Taizhou 317300, China;3. Xinsheng Middle School, Hengxi Town, Xianju County, Zhejiang Taizhou 317312, China;4. Chicheng Middle School, Tiantai County, Zhejiang Taizhou 317200, China)

In recent decades, the research on the teaching of problem posing has been fruitful. The theoretical framework of the cognitive relationship between problem posing and problem solving, the relationship between mathematics and students’ academic achievement, teaching strategies and teaching models has become increasingly mature. However, the case studies of teaching practice are not extensive and in-depth, especially the cases that use data to illustrate the teaching effect are few. Taking the content of the “Isosceles Triangle” unit of junior high school as an example, the study puts forward the teaching strategy of “leading with big ideas, based on the holistic teaching design of the unit, integrating existing problem posing teaching methods, and promoting students to pose and solve high-value problems”. The samples were selected in typical urban schools and rural schools forthe comparative teaching experiment. The data were collected and analyzed with SPSS20.0 software, and further Effect Size (ES) analysis was conducted. The results show that this teaching strategy can significantly improve students’ ability to pose and solve high-value mathematical problems.

isosceles triangle; problem posing and solving; comparative teachingexperiment

G632.4

A

1004–9894（2022）01–0042–10

吳增生，鄭燕紅，吳海燕，等．怎樣促進學生提出和解決高價值的數學問題——等腰三角形單元教學對比實驗研究[J]．數學教育學報，2022，31（1）：42-51．

2021–10–01

人民教育出版社義務教育課標教材《圖形與幾何》專題研究（KC2019-057）

吳增生（1962—），男，浙江仙居人，特級教師，正高級教師，浙江師范大學教育碩士導師，教育部第三批國培專家，主要從事中學數學教育研究．

[責任編校：陳漢君、陳雋]