大規(guī)模工程電磁場的億自由度可擴展并行計算方法

金 亮 李育增 楊慶新 張 闖 閆 帥

大規(guī)模工程電磁場的億自由度可擴展并行計算方法

金 亮1,2李育增1,2楊慶新1,2張 闖1,2閆 帥3

（1. 省部共建電工裝備可靠性與智能化國家重點實驗室（河北工業(yè)大學(xué)） 天津 300130 2. 河北省電磁場與電器可靠性重點實驗室（河北工業(yè)大學(xué)） 天津 300130 3. 中國科學(xué)院電工研究所 北京 100081）

精確和快速的電磁場計算，是電工裝備精細(xì)模擬和優(yōu)化設(shè)計的基礎(chǔ)。該文在高性能云平臺的高速互聯(lián)彈性集群上開展可擴展并行計算研究，使用OpenMpi作為消息傳遞庫，選取的區(qū)域分解算法為對偶原始有限元撕裂內(nèi)聯(lián)（FETI-DP）法，通過改進主從/對等的并行程序框架實現(xiàn)電導(dǎo)率不變時渦流場磁矢勢的并行計算，在降低編程復(fù)雜度的同時提高了并行計算效率。使用C語言編寫程序，用國際TEAMProblem7基準(zhǔn)問題驗證可擴展并行計算方法。該文將主從/對等并行程序框架和對偶原始有限元撕裂內(nèi)聯(lián)（FETI-DP）法引入電磁計算領(lǐng)域，提高了并行計算效率和可擴展性，為大規(guī)模工程電磁場計算提供了一種新的實踐和理論方法。

并行計算 電磁場數(shù)值計算 有限元法 對偶原始有限元撕裂內(nèi)聯(lián)法

0 引言

現(xiàn)代電工裝備是支撐智能電網(wǎng)和國家重點重大項目的關(guān)鍵裝備。在向高技術(shù)參數(shù)的發(fā)展過程中，現(xiàn)代電工裝備的設(shè)計需考慮性能優(yōu)化、制造工藝約束、服役特性和極限工作條件，因而計算電磁學(xué)對于精細(xì)模擬的作用日益凸顯[1-2]。

對于計算電磁學(xué)而言，有限元法（Finite Element Method, FEM）是一種強大的電磁場數(shù)值計算方法，它具有模擬復(fù)雜介質(zhì)和精細(xì)幾何的能力。由于普通計算機的計算能力無法滿足電工裝備精細(xì)模擬的計算需求，導(dǎo)致以下幾個問題：一是常使用簡化數(shù)值模型降低計算量，其計算結(jié)果的可信度降低。如大型電力變壓器垂直漏磁場導(dǎo)致的渦流和磁滯損耗計算問題，一般采用將多層硅鋼片進行整體等效的方法，導(dǎo)致局部熱點計算難以反映實際情況[3]。二是對于含縫隙或小氣隙的多尺度（空間）問題，網(wǎng)格精度滿足不了實際要求。如存在mm級縫隙的m級裝備——特大型電機、近零磁場環(huán)境裝置等，由于尺寸差距過大導(dǎo)致設(shè)計指標(biāo)與實際性能具有巨大差別[4]。三是受計算速度限制，一些精細(xì)模擬難以完成，產(chǎn)品級精細(xì)模型的計算面臨計算時間過長的問題[5]。如特高壓變壓器的仿真計算需要多組工況的計算，而一次計算需要幾天甚至幾十天的時間。

面對大型而復(fù)雜的計算問題，并行計算是提高計算效率的有效方法之一。在電工領(lǐng)域中，并行計算方法已經(jīng)被廣泛應(yīng)用以提高計算效率。如文獻[6]提出了利用圖數(shù)據(jù)庫對電力系統(tǒng)進行建模、并在圖內(nèi)存數(shù)據(jù)庫上進行圖并行計算的方法，相比于傳統(tǒng)串行計算的能量管理系統(tǒng)，在線潮流和靜態(tài)安全分析的速度上有顯著的提高。文獻[7]提出了一種基于CPU-GPU異構(gòu)的靜態(tài)電壓穩(wěn)定域邊界并行計算方法，避免了直接法計算量大、計算復(fù)雜度高的缺陷，提高了靜態(tài)電壓穩(wěn)定域的搜索效率。文獻[8]提出了一種基于多核并行計算的有限集模型預(yù)測算法（Finite Control Set Model Predictive Control, FCS-MPC），有效降低了傳統(tǒng)FCS-MPC算法的執(zhí)行時間。針對計算精度高的大規(guī)模工程有限元法在電磁場計算方面耗時長的問題，并行計算是有效的解決方法之一[9]。為了有效解決大規(guī)模計算問題，在高頻大尺寸領(lǐng)域一般采用將整個計算域劃分為更小子域的有限元區(qū)域分解法[10-12]。如，采用魯棒的區(qū)域分解方法——對偶原始有限元撕裂內(nèi)聯(lián)法（Dual-PrimalFinite Element Tearing and Interconnecting, FETI-DP）解決多尺度有限元建模問題[13]；使用區(qū)域分解法，在子域之間采用不連續(xù)的Galerkin方法提高不連續(xù)結(jié)構(gòu)的電磁計算收斂性[14]。針對工頻或低頻電工裝備，計算效率較高的單元接單元（Element by Element, EBE）并行有限元法在渦流場計算領(lǐng)域得到了初步應(yīng)用和原理性驗證[15]。大型電工裝備的硅鋼片，由于每片厚度僅為0.1～0.5mm，三維有限元建模和渦流計算困難，采用基于信息傳遞接口（Massage Passing Interface, MPI）和非結(jié)構(gòu)化四面體網(wǎng)格的并行有限元程序可高效完成百萬自由度的計算[16]。為了推廣并行計算的使用范圍和收斂性，LU重組方法可使近似奇異的有限元矩陣得到正則化，適用于大型渦流、開關(guān)磁阻電機和隨鉆測井問題[17]。目前，有限元并行計算方法在國內(nèi)外工程領(lǐng)域的現(xiàn)實需求使其得到了快速的發(fā)展[18-20]。并行計算的應(yīng)用從結(jié)構(gòu)動力分析、地球物理發(fā)展到高頻電磁場、工頻和低頻電磁場，甚至是電力系統(tǒng)以及靜態(tài)電磁場等方面[21-28]。在電氣領(lǐng)域，由于大型電機、變壓器等電工設(shè)備或應(yīng)用電磁原理大型裝備的容量和規(guī)模越來越大，對于精細(xì)模擬的要求越來越高、計算規(guī)模的需求也日趨龐大。為滿足電磁精細(xì)模擬對于計算規(guī)模、易用性的需求，高性能公有云、私有云和混合云成為高性能計算的一種有效解決方法[29-31]。

在巖土工程數(shù)值模擬領(lǐng)域，并行計算技術(shù)已經(jīng)發(fā)展到百萬、千萬乃至億自由度的計算規(guī)模[32-34]。目前，三維工程電磁場的有限元計算及其并行方法的計算規(guī)模多為數(shù)百萬自由度的線性和非線性問題。計算規(guī)模、計算時間方面尚不能滿足特大型電機、變壓器等電工設(shè)備或應(yīng)用電磁原理大型裝備的工程和科學(xué)計算需求。

因而本文在百萬自由度的電磁并行計算方法研究基礎(chǔ)上[35-36]，提出一種基于OpenMpi的億自由度高效可擴展并行計算方法。首先搭建云計算彈性集群，改進主從/對等模型，并建立并行程序框架，推導(dǎo)電導(dǎo)率不變時的渦流場磁矢勢法，推導(dǎo)并論述FETI-DP區(qū)域分解算法的收斂性和魯棒性，最后使用國際TEAM Problem 7案例驗證了億自由度可擴展并行計算方法。

1 計算集群

云計算主要使用虛擬化、分布式存儲技術(shù)將計算機集群的計算資源、存儲資源、網(wǎng)絡(luò)及相關(guān)服務(wù)組成資源池。對于用戶，云計算即為三個層次服務(wù)：Infras-tructure as a Service（IaaS），Platform as a Service（PaaS）和Software as a Service（SaaS）。基于云計算的有限元仿真系統(tǒng)如圖1所示。圖中，SSL為安全套接字協(xié)議（Secure Sockets Layer），JSCH為安全外殼協(xié)議（Secure Shell, SSH）的純Java實現(xiàn)，KVM為基于內(nèi)核的虛擬機（Kernel-based Virtual Machine, KVM）。從IaaS 到SaaS（從硬件到軟件或服務(wù)），用戶可按照自己的計算需求從資源池中獲得動態(tài)易擴展、可管理的資源及服務(wù)。

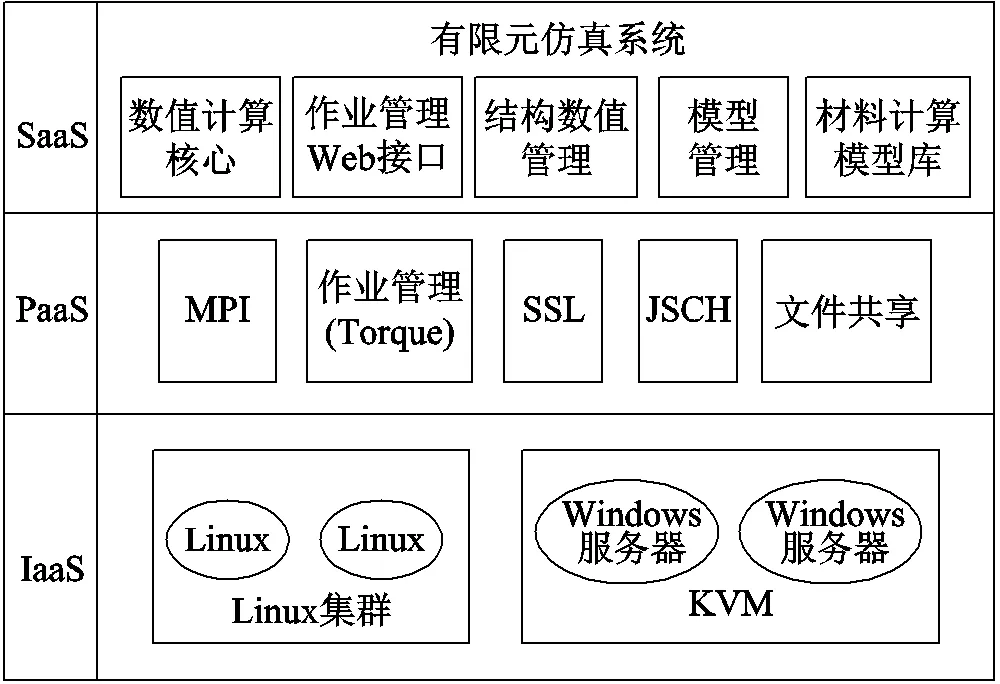
圖1 基于云計算的有限元仿真系統(tǒng)

對于高性能計算，云計算一般采用管理節(jié)點虛擬化和計算節(jié)點非虛擬化的混合架構(gòu)。計算機集群由21臺雙路28核心、128GB內(nèi)存的服務(wù)器組成。1臺作為管理節(jié)點（Master），負(fù)責(zé)計算任務(wù)的分發(fā)和調(diào)度，其余20臺作為計算節(jié)點（Slaver）實現(xiàn)計算與存儲。集群之間通過Infiband協(xié)議實現(xiàn)30Gbit/s光纖互聯(lián)。存儲系統(tǒng)采用Hadoop 分布式文件系統(tǒng)（Hadoop Distributed File System, HDFS）。

2 有限元可擴展并行算法

可擴展并行計算是指并行算法能有效利用可擴展處理器核心數(shù)的能力。并行程序計算性能的下降主要是由于數(shù)值計算過程中迭代計算需要在不同處理器核心及不同節(jié)點之間將OpenMpi通信用于交換邊界數(shù)據(jù)。在主從模式，由于所有的數(shù)據(jù)通信均需通過管理節(jié)點實現(xiàn)，因此通信時間隨核心數(shù)和計算規(guī)模的增加急劇增加導(dǎo)致，其計算效能在大規(guī)模計算中下降嚴(yán)重。本文主要通過子進程間直接進行點對點的通信且子進程間完全對等的方法改進傳統(tǒng)的主從模式，建立基于主從/對等模型的并行程序框架，在實現(xiàn)進程間的高效交換邊界數(shù)據(jù)的同時，兼顧主從模式程序清晰易調(diào)試的優(yōu)點。具體為：任務(wù)分配采用主從模式，分區(qū)取得子任務(wù)進入有限元計算后，子進程與子進程間直接進行點對點的通信，且子進程間完全對等。

2.1 并行程序框架

并行程序框架如圖2所示。圖中主程序、主進程、從進程、前處理數(shù)據(jù)讀取模塊為并行、串行相一致的程序或模塊；剖分與數(shù)據(jù)分割模塊、剖分模塊、數(shù)據(jù)分發(fā)模塊、數(shù)據(jù)接收模塊、求解器同步模塊為并行計算模塊；求解器、結(jié)果輸出模塊、子程序通信模塊為并行獨有模塊。首先采用前處理數(shù)據(jù)讀取Gidpre模塊讀入有限元前處理數(shù)據(jù)，通過剖分與數(shù)據(jù)分割Mpartition模塊對全局的有限元數(shù)據(jù)進行任務(wù)分割，并結(jié)合有限元剖分Mgetpart模塊將對應(yīng)各子分區(qū)的數(shù)據(jù)和細(xì)剖分指令發(fā)送到對應(yīng)子進程。子進程的數(shù)據(jù)接收Spart、自由度處理和解初始化Spre、剛度矩陣Sgetpart等模塊完成從主進程接收分配的區(qū)域任務(wù)數(shù)據(jù)，并進一步細(xì)化網(wǎng)格和組裝剛度矩陣。然后各子進程使用求解器Starta、子進程通信testa、求解器Ssolv等模塊完成有限元求解流程和數(shù)據(jù)通信。各子進程間的點對點通信完成數(shù)據(jù)交換是在求解器Ssolv模塊求解過程中每一次迭代計算子程序完畢后進行，通過通信模塊Scom完成。

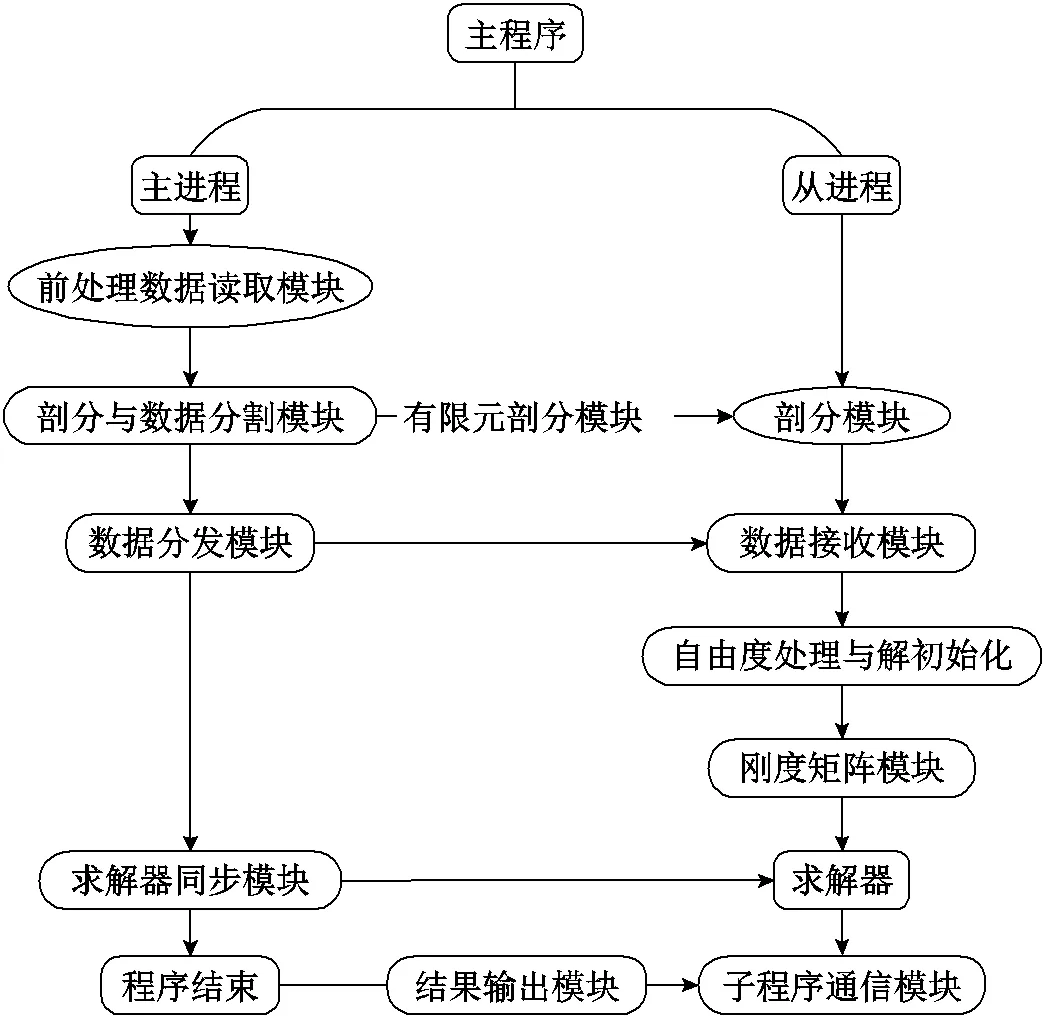
圖2 并行程序框架

2.2 基于OpenMpi的并行程序通信

OpenMpi的工作機制如圖3所示。MPI作為消息傳遞接口是一個并行計算的應(yīng)用程序接口，能協(xié)調(diào)多臺主機間的并行計算，且并行規(guī)模上的可伸縮性很強。基于組件架構(gòu)MPI實現(xiàn)的OpenMpi，可通過組合不同組件來實現(xiàn)不同的功能，具有靈活、高效、適用性高等特點，適用于分布式內(nèi)存之間的信息通信。主從/對等模型使得并行計算框架具有高度并行化的特點。為實現(xiàn)億自由度的并行計算規(guī)模，并行計算框架運行在由多個計算節(jié)點組成的集群系統(tǒng)中，是典型的分布式內(nèi)存系統(tǒng)，本文采用OpenMpi實現(xiàn)對本地指令和數(shù)據(jù)的直接訪問以及管理節(jié)點和計算節(jié)點之間的消息傳遞。由MPI層、點對點傳輸層（PML）、字節(jié)傳輸層（BTL）、BTL管理層四部分組成的節(jié)點間通信架構(gòu)，如圖4所示。MPI層的作用是為MPI程序提供程序接口；在PML中，BTL組件管理所有的消息傳遞，實現(xiàn)了點對點通信原語，MPI層點對點語義通過PML運行，消息調(diào)度與進程策略嵌于協(xié)議中；由于多種功能組件需要BTL組件，BTL管理層（BML）給BTL的初始化與通過BTL進行資源恢復(fù)提供工具，在BTL初始化完成后，BML層對于BTL的內(nèi)聯(lián)功能被有效略過；BTL層架構(gòu)包含了一組RDMA的通信單元，通過發(fā)送/接收端與基于RDMA端之間的內(nèi)部數(shù)據(jù)連接實現(xiàn)數(shù)據(jù)轉(zhuǎn)換的統(tǒng)一方法，以上四部分實現(xiàn)了節(jié)點間消息傳遞功能。基于進程調(diào)度的OpenMpi，并行擴展能力強，可滿足成千上萬計算節(jié)點的并行需求，且計算效率最高，但將串行程序并行化需要大量修改原有的串行代碼和架構(gòu)，導(dǎo)致編程工作量大、調(diào)試難度很大。本文的程序采用C語言編寫，并在架構(gòu)上考慮了并行的需要，因而采用OpenMpi實現(xiàn)并行指令和數(shù)據(jù)的通信和管理，達(dá)到提高并行計算效率的目的。同時采用了檢查點設(shè)置/回卷恢復(fù)功能，建立進程、節(jié)點失效恢復(fù)的容錯系統(tǒng)。

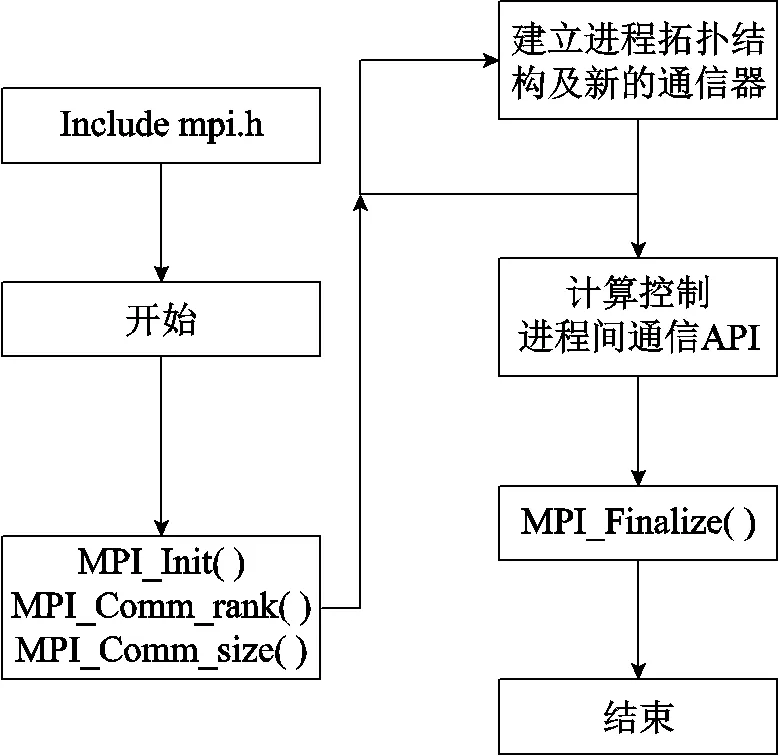
圖3 OpenMpi工作機制

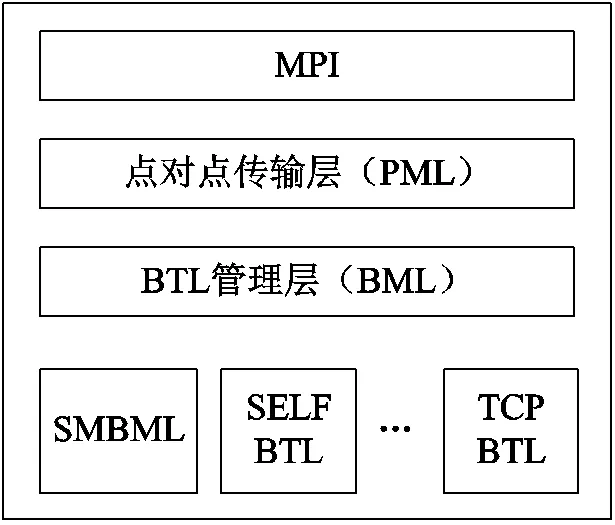
圖4 節(jié)點間通信架構(gòu)

2.3 電導(dǎo)率不變時的渦流場磁矢勢A法

在渦流區(qū)內(nèi)，在忽略位移電流的情況下，Maxwell方程可寫作[37]

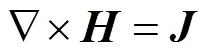
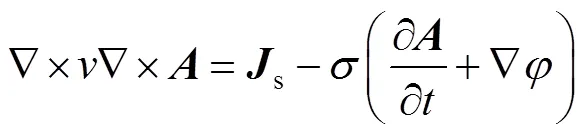
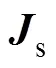
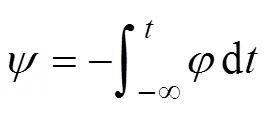
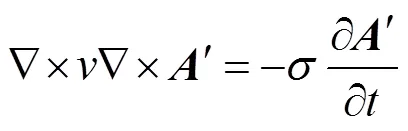
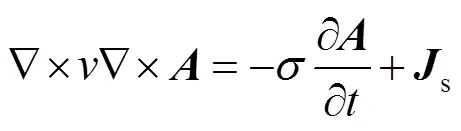
當(dāng)源電流隨時間按正弦變化，矢量可用復(fù)數(shù)計算。于是式（6）成為復(fù)矢量方程的三維渦流場矢量磁位微分方程及其邊值問題，即

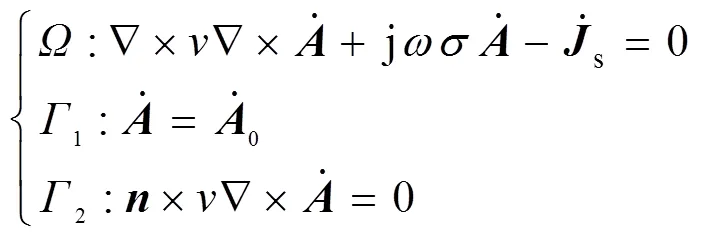
式（7）可通過伽遼金方法，可以得到一個線性方程的有限元系統(tǒng)

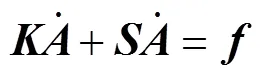
式中

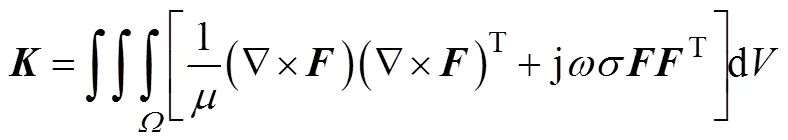
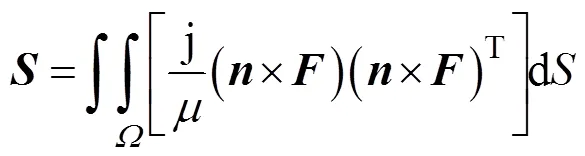
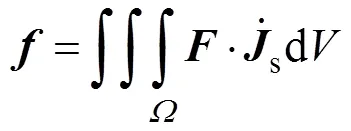
最后，電場強度表達(dá)式為

2.4 區(qū)域分解和并行算法

為了處理規(guī)模較大的模型，本文采用多層劃分框架Metis。Metis是一組串行程序，用于對圖進行分區(qū)、對有限元網(wǎng)格進行分區(qū)以及為稀疏矩陣生成填充順序。Metis中的算法是基于多級遞歸對分、多級路和多約束分區(qū)方案。

區(qū)域分解方法（Domain Decomposition Method, DDM）將原來的大規(guī)模問題分解成更小的子域問題，并使用并行計算方法對其進行獨立處理，從而使總計算時間顯著縮短。并行算法采用一種魯棒的區(qū)域分解方法——對偶原始有限元撕裂內(nèi)聯(lián)法（FETI-DP）提高有限元計算效率和擴展能力[22]。

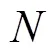
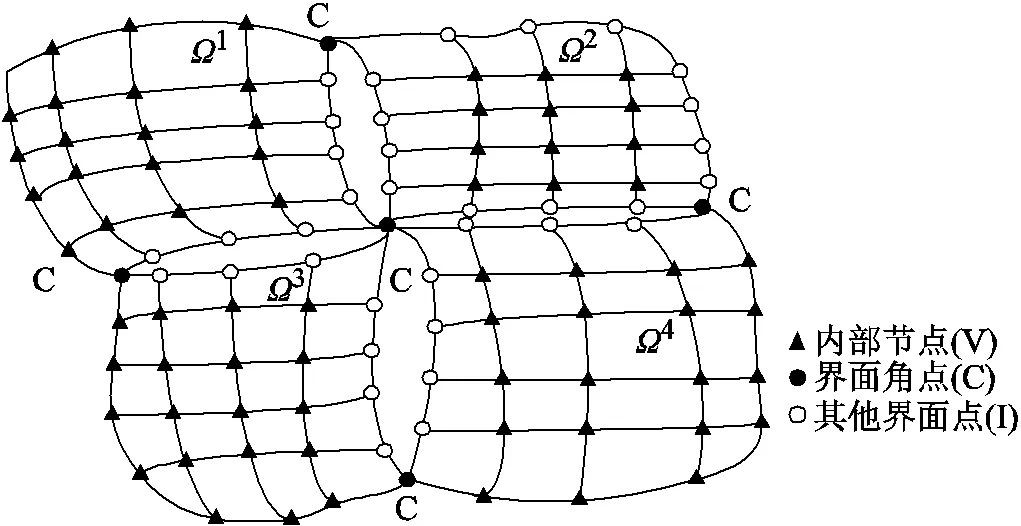
圖5 FETI-DP 算法網(wǎng)格剖分及節(jié)點分類

在每個子域界面上，應(yīng)滿足場量的連續(xù)性，即

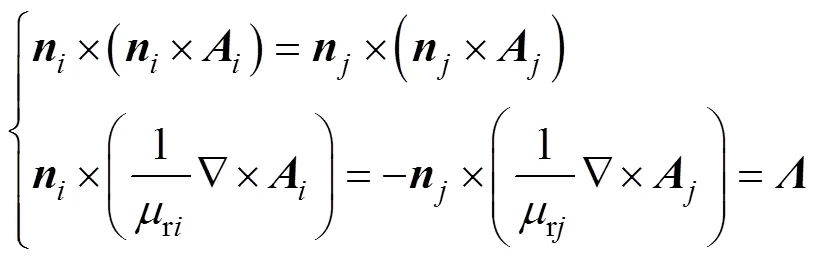
式中，、為兩個相鄰子域的編號。

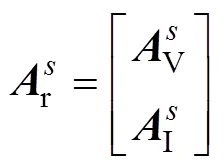
則有限元的子域剛度方程可定義為

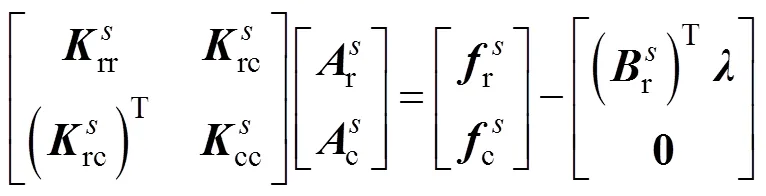
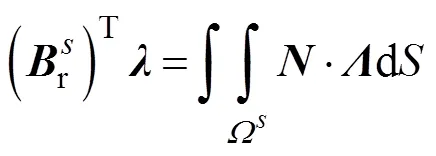
子域分界面上的連續(xù)性方程可表示為

通過矩陣運算，由式（15）、式（16）與式（17）消去分界面的自由度，可以將原問題轉(zhuǎn)變?yōu)榍蠼怅P(guān)于界面拉格朗日乘子的一個對稱正定對偶問題，即

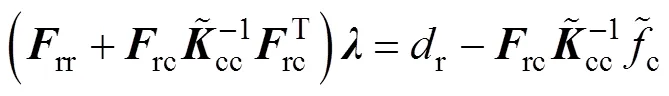
其中

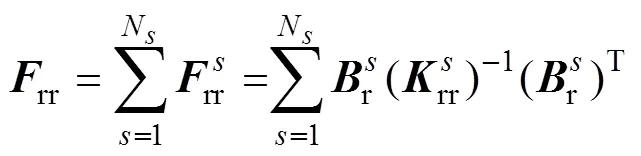
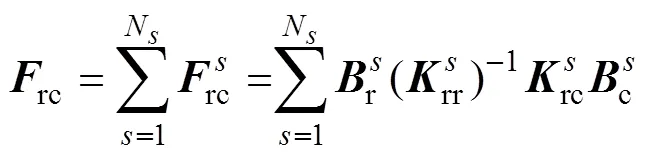
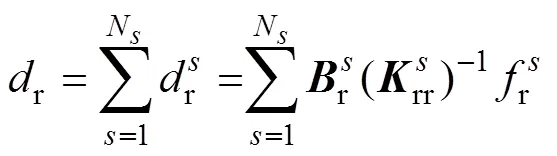
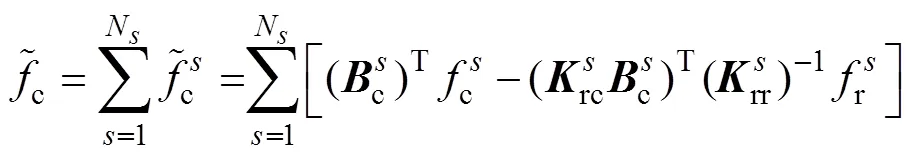
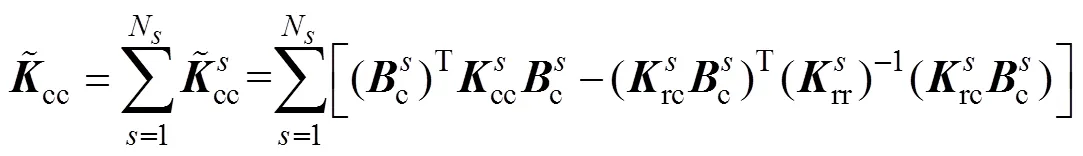
通過求解式（18）得到，然后將代入式（15）求得子域的，進而得到全局。由于原問題轉(zhuǎn)變?yōu)榍蠼怅P(guān)于界面拉格朗日乘子的一個對稱正定對偶問題，F(xiàn)ETI-DP方法具有良好的擴展性和收斂性。

3 計算案例

并行算法的實現(xiàn)是基于FELAC計算平臺，具體實現(xiàn)過程，如圖2所示。OpenMpi采用基于intel 14.0.2編譯器編譯的mpi。操作系統(tǒng)為Red Hat 6.5，內(nèi)核版本為2.6.32-431.TH.x86_64。單機串行程序在Felac開發(fā)平臺上開發(fā)完成，并行程序在上述的軟硬件環(huán)境下開發(fā)、運行和測試。

π的并行計算程序在計算集群多節(jié)點上的并行程序測試，如圖6所示。

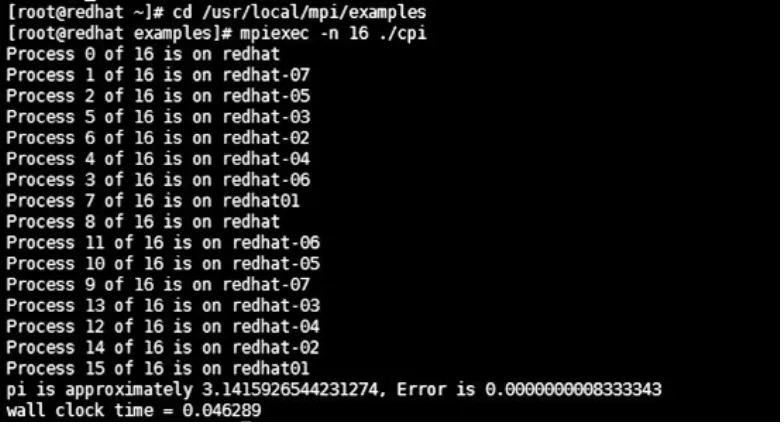
圖6 多節(jié)點并行程序測試

國際TEAM（Testing Electormagnetic Analysis Methods）基準(zhǔn)問題是為了測試和驗證電磁工程問題的電磁場數(shù)值計算方法正確性而建立的一系列標(biāo)準(zhǔn)模型和案例。TEAM Problem 7是檢驗三維渦流場數(shù)值計算精度的標(biāo)準(zhǔn)模型，由矩形載流線圈和導(dǎo)體板組成，線圈通以正弦電流，如圖7a所示。矩形載流線圈一般由絕緣漆包銅線繞制，導(dǎo)體板一般為鋁板。可用于模擬電工設(shè)備中金屬構(gòu)件的交變漏磁場引起的損耗。

可由式（12）計算電場強度，鋁板中感應(yīng)渦流密度e的求解公式為

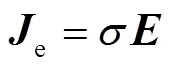
磁通密度計算公式為

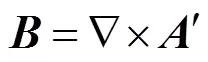
采用多層劃分框架Metis對含空氣域的整體進行分區(qū)后的情況，如圖7b所示。由于矩形載流線圈和導(dǎo)體板均為非導(dǎo)磁性材料，磁場和電場分布在一個比較大的空間內(nèi)并考慮到幾何結(jié)構(gòu)為方形，因此包含矩形載流線圈和導(dǎo)體板的空氣域為方形結(jié)構(gòu)。采用多層劃分框架Metis對線圈和導(dǎo)體板進行分區(qū)后的情況，如圖7a所示。從圖7a和圖7b可知多層劃分框架Metis可對求解域進行區(qū)域分解，且分區(qū)較為規(guī)則和均勻。

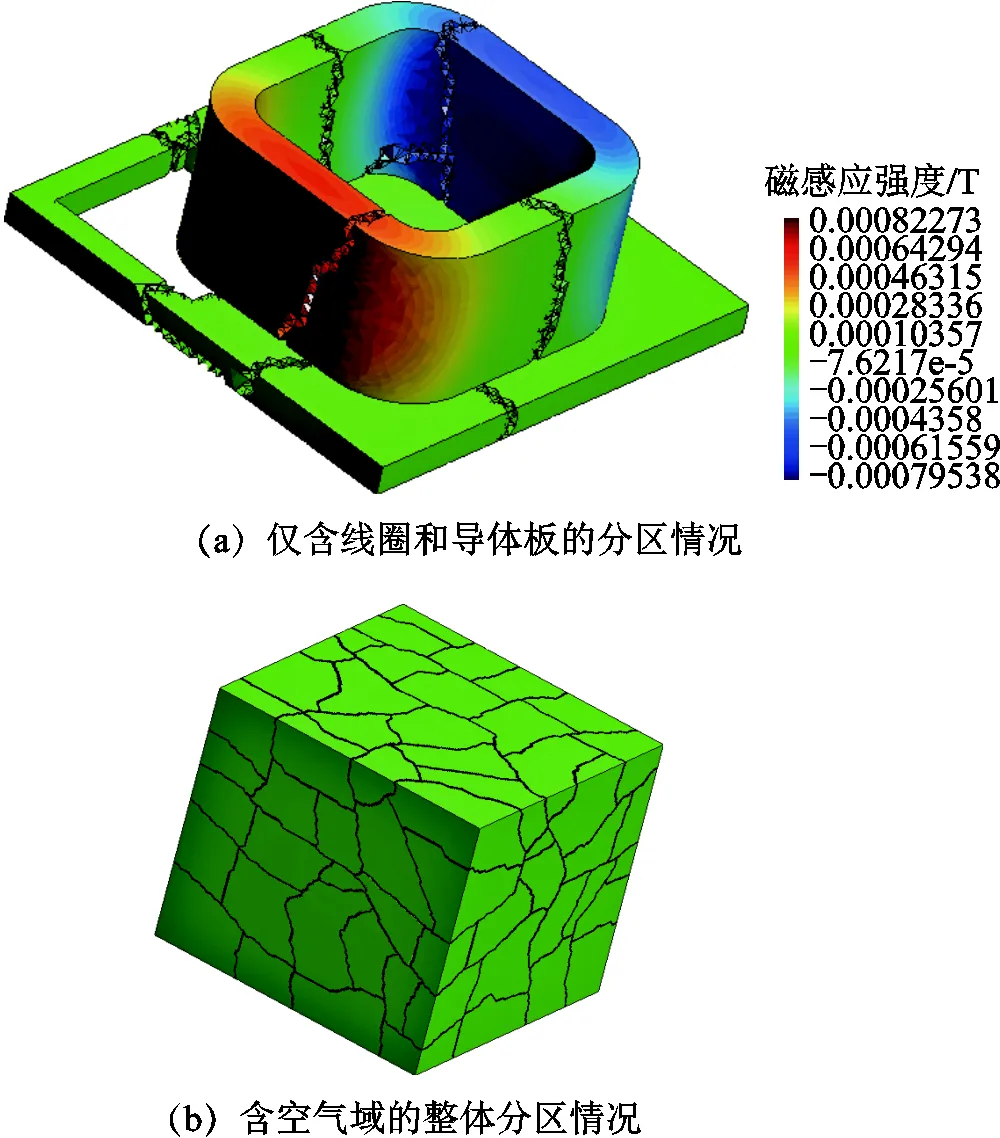
圖7 TEAM Problem 7基準(zhǔn)問題計算案例

200Hz時導(dǎo)體板上表面電流分量分布如圖8所示。電流虛部和實部的分布情況和電磁感應(yīng)定律是一致的，電流在矩形載流線圈正下方的導(dǎo)體板開孔邊界處最大、在遠(yuǎn)離矩形載流線圈的導(dǎo)體板外邊緣處最小。

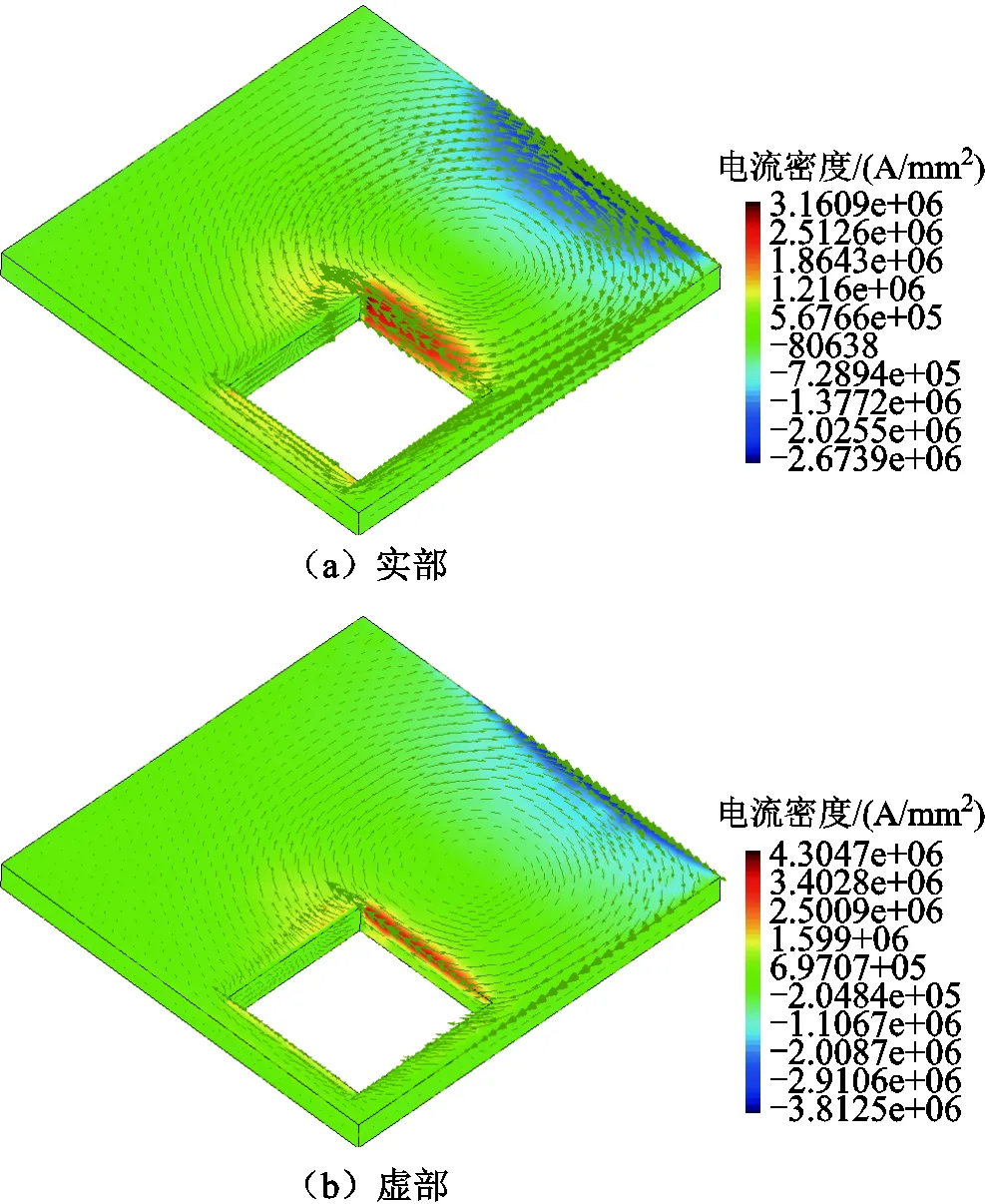
圖8 200Hz時導(dǎo)體板上表面電流Y分量分布

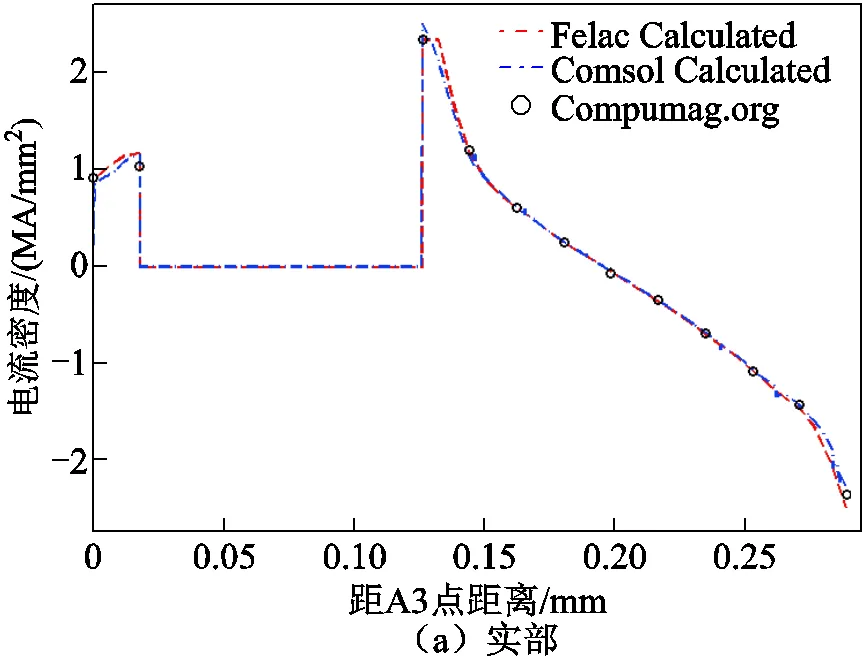
200Hz時空氣中A3-B3直線上磁場分量的計算值和測量值，如圖9所示。其中，直線A3-B3是指Team Problem7文獻中給出的測量線[39]。A3-B3是緊鄰導(dǎo)體板上表面的一條位于空中的直線，A3坐標(biāo)值為（0mm, 72mm, 34mm），B3坐標(biāo)值為（288mm, 72mm, 34mm）。圖9中的Felac Calculated是指可擴展并行計算方法得到的計算值；Comsol Calculated是指電磁場數(shù)值計算軟件Comsol計算得到的計算值；Compumag. org是指Team Problem7文獻中給出的測量值[39]，結(jié)果證明本文并行計算方法的計算結(jié)果是正確的。

1）小規(guī)模測試

有限元的測試規(guī)模為節(jié)點330萬、自由度2 643萬、單元數(shù)2 091萬，為評價并行計算的效率，分別采用100核、200核、300核和400核進行測試。加速比為單個CPU計算運行時間s與個CPU計算運行時間p()之間的比值p()=s/p()。個CPU的并行計算效率為p()=p()/，并行效率可以理解為每個CPU的平均利用率。以100核作為基準(zhǔn)的并行性能見表1。

表1 小規(guī)模測試的并行性能

Tab.1 Performance for small-scale testing

2）大規(guī)模測試

有限元的測試規(guī)模為節(jié)點數(shù)1 256萬、自由度數(shù)10 049萬、單元數(shù)7 436萬。為評價并行計算的效率，分別采用100核、200核、300核、400核進行測試，以100核作為基準(zhǔn)的并行性能見表2。

節(jié)點數(shù)、自由度數(shù)、單元數(shù)的數(shù)量將會影響計算規(guī)模的大小。隨著計算規(guī)模的增加將會使并行計算過程的迭代計算時間和并行計算總時間明顯增加。對比兩個測試結(jié)果，采用100核、200核、300核、400核時，大規(guī)模測試的計算效率相比小規(guī)模測試變化不大。實驗結(jié)果證明本文提出的大規(guī)模工程電磁場億自由度可擴展并行計算方法具有很好的并行計算效率和魯棒性。

表2 大規(guī)模測試的并行性能

Tab.2 Performance for big-scale testing

4 結(jié)論

本文研究并改進傳統(tǒng)的主從并行程序框架，建立了主從/對等并行程序框架，基于電導(dǎo)率不變時渦流場磁矢勢法和對偶原始有限元撕裂內(nèi)聯(lián)（FETI-DP）法建立了可擴展并行計算方法，調(diào)用400個計算核心實現(xiàn)了渦流場的高效并行計算，成功地將數(shù)值計算規(guī)模提高到1億自由度。數(shù)值計算的加速比結(jié)果表明可擴展并行計算方法具有很好的可擴展性能和很高的并行計算效能，同時點對點的對等模型為更大規(guī)模的并行數(shù)值計算奠定了基礎(chǔ)。研究成果為大型復(fù)雜電工裝備產(chǎn)品級模型的高效和高精度數(shù)值模擬提供了有效的理論和實踐方法。

在后續(xù)研究中，將進一步提高并行計算規(guī)模和加速比，基于A-phi方法實現(xiàn)TEAM Problem21案例的實現(xiàn)億節(jié)點并行計算。

[1] Cheng Zhiguang, Norio Takahashi, Yang Sumei, et al. Loss spectrum and electromagnetic behavior of Problem 21 family[J]. IEEE Transactions on Magnetics, 2006, 42(4): 1467-1470.

[2] 謝德馨, 程志光, 楊仕友, 等. 對當(dāng)前計算電磁學(xué)發(fā)展的觀察與思考——參加COMPUMAG2011會議有感[J]. 電工技術(shù)學(xué)報, 2013, 28(1): 136-141.

Xie Dexin, Cheng Zhiguang, Yang Shiyou, et al. Observation and consideration on the current development of computational electromagnetics—in perspective of COMPUMAG2011[J]. Transactions of China Electrotechnical Society, 2013, 28(1): 136-141.

[3] Hihat Nabil, Napieralska-Juszczak Ewa, Lecointe Jean-Philippe, et al. Equivalent permeability of step-lap joints of transformer cores: computational and experimental considerations[J]. IEEE Transactions on Magnetics, 2011, 47(1): 244-251.

[4] 李立毅, 孫芝茵, 潘東華, 等. 近零磁環(huán)境裝置現(xiàn)狀綜述[J]. 電工技術(shù)學(xué)報, 2015, 30(15): 136-140.

Li Liyi, Sun Zhiyin, Pan Donghua, et al. Status reviews for nearly zero magnetic field environment facility[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 136-140.

[5] 程志光, 劉濤, 范亞娜, 等. 基于TEAM P21三維雜散場問題建模仿真與驗證[J]. 電工技術(shù)學(xué)報, 2014, 29(9): 194-203.

Cheng Zhiguang, Liu Tao, Fan Yana, et al. TEAM P21-based validation of 3-D stray-field modeling and simulation[J]. Transactions of China Electrotechnical Society, 2014, 29(9): 194-203.

[6] 劉廣一, 戴仁昶, 路軼, 等. 基于圖計算的能量管理系統(tǒng)實時網(wǎng)絡(luò)分析應(yīng)用研發(fā)[J]. 電工技術(shù)學(xué)報, 2020, 35(11): 2339-2348.

Liu Guangyi, Dai Renchang, Lu Yi, et al. Graph computing based power network analysis applications[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2339-2348.

[7] 李雪, 張琳瑋, 姜濤, 等. 基于CPU-GPU異構(gòu)的電力系統(tǒng)靜態(tài)電壓穩(wěn)定域邊界并行計算方法[J]. 電工技術(shù)學(xué)報, 2021, 36(19): 4070-4084.

Li Xue, Zhang Linwei, Jiang Tao, et al. CPU-GPU heterogeneous computing for static voltage stability region boundary in bulk power systems[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4070-4084.

[8] 劉濤, 習(xí)金玉, 宋戰(zhàn)鋒, 等. 基于多核并行計算的永磁同步電機有限集模型預(yù)測控制策略[J]. 電工技術(shù)學(xué)報, 2021, 36(1): 107-119.

Liu Tao, Xi Jinyu, Song Zhanfeng, et al. Finite control set model predictive control of permanent magnet synchronous motor based on multi-core parallel computing[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 107-119.

[9] 管建和. 電磁場有限元法解釋分布式并行計算的研究[D]. 北京: 中國地質(zhì)大學(xué)（北京）, 2006.

[10] Li Yujia, Jin Jianming. A new dual-primal domain decomposition approach for finite element simulation of 3-D large-scale electromagnetic problems[J]. IEEE Transactions on Antennas and Propagation, 2007, 55(10): 2803-2810.

[11] Zhen Peng, Lee JinFa. Non-conformal domain decomposition method with mixed true second order transmission condition for solving large finite antenna arrays[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(5): 1638-1651.

[12] Xue Mingfeng, Jin Jianming. A hybrid conformal/ nonconformal domain decomposition method for multi-region electromagnetic modeling[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(4): 2009-2021.

[13] Xue Mingfeng, Jin Jianming. Nonconformal FETI-DP methods for large-scale electromagnetic simulation[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(9): 4291-4305.

[14] Mario A Echeverri Bautista, Francesca Vipiana, Matteo Alessandro Francavilla, et al. A nonconformal domain decomposition scheme for the analysis of multiscale structures[J]. IEEE Transactions on Antennas and Propagation, 2015, 63(8): 3548-3560.

[15] 唐任遠(yuǎn), 吳東陽, 謝德馨. 單元級別并行有限元法求解工程渦流場的關(guān)鍵問題研究[J]. 電工技術(shù)學(xué)報, 2014, 29(5): 1-8.

Tang Renyuan, Wu Dongyang, Xie Dexin. Research on the key problem of element by element parallel FEM applied to engineering eddy current analysis[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 1-8.

[16] Zheng Weiying, Cheng Zhiguang. An inner-constrained separation technique for 3D finite element modeling of GO silicon steel laminations[J]. IEEE Transactions on Magnetics, 2012, 48(8): 2277-2283.

[17] Wang Yao, Jin Jianming, Philip TKrein. Application of the LU recombination method to the FETI-DP method for solving low-frequency multiscale electromagnetic problems[J]. IEEE Transactions on Magnetics, 2013, 49(10): 5346-5355.

[18] Van Emden Henson, Ulrike Meier Yang. BoomerAMG: a parallel algebraic multigrid solver and preconditioner[J]. Applied Numerical Mathematics, 2002, 41(1): 155-177.

[19] Ralf Hiptmair, Xu Jinchao. Auxiliary space preconditioning for edge elements[J]. IEEE Transactions on Magnetics, 2008, 44(6): 938-941.

[20] Zhang Linbo. A parallel algorithm for adaptive local refinement of tetrahedral meshes using bisection[J]. Numerical Mathematics a Journal of Chinese Universities English Series, 2009, 2(1): 65-89.

[21] George Karypis, Vipin Kumar. Multilevel k-way partitioning scheme for irregular graphs[J]. Journal of Parallel and Distributed Computing, 1998, 48(1): 96-129.

[22] Charbel Farhat, Michel Lesoinne, Patrick LeTallec, et al. FETI-DP: a dual–primal unified FETI method—Part I: a faster alternative to the two-level FETI method[J]. International Journal for Numerical Methods in Engineering, 2001, 50(7):1523-1544.

[23] Xue Mingfeng, Jin Jianming. A preconditioned dual-primal finite element tearing and interconnecting method for solving three-dimensional time-harmonic Maxwell's equations[J]. Journal of Computational Physics, 2014, 274: 920-935.

[24] James Ahrens, Kristi Brislawn, Ken Martin, et al. Large-scale data visualization using parallel data streaming[J]. IEEE Computer Graphics and Applications, 2001, 21: 34-41.

[25] 史燕琨, 熊華強. 基于偽并行遺傳算法的配電網(wǎng)電容器優(yōu)化配置[J]. 電力系統(tǒng)保護與控制, 2009, 37(20): 57-60.

Shi Yankun, Xiong Huaqiang. Optimal capacitor arrangement based on pseudo parallel genetic algorithm[J]. Power System Protection and Control, 2009, 37(20): 57-60.

[26] 黃靖, 張曉鋒, 葉志浩. 大型船舶電力系統(tǒng)分布式并行潮流計算方法[J]. 電力系統(tǒng)保護與控制, 2011, 39(7): 50-55.

Huang Jing, Zhang Xiaofeng, Ye Zhihao. A distributed parallel load flow calculation method for large ship power system[J]. Power System Protection and Control, 2011, 39(7): 50-55.

[27] 簡金寶, 楊林峰, 全然. 基于改進多中心校正解耦內(nèi)點法的動態(tài)最優(yōu)潮流并行算法[J]. 電工技術(shù)學(xué)報, 2012, 27(6): 232-241.

Jian Jinbao, Yang Linfeng, Quan Ran. Parallel algorithm of dynamic optimal power flow based on improved multiple centrality corrections decoupling interior point method[J]. Transactions of China Electrotechnical Society, 2012, 27(6): 232-241.

[28] David MFernández, Maryam Mehri Dehnavi, Warren JGross, et al. Alternate parallel processing approach for FEM[J]. IEEE Transactions on Magnetics, 2012, 48(2): 399-402.

[29] Gabriel Mateescu, Wolfgang Gentzsch, Calvin JRibbens. Hybrid computing—where HPC meets grid and cloud computing[J]. Future Generation Computer Systems, 2011, 27(5): 440-453.

[30] Ismail Ari, Nitel Muhtaroglu. Design and implementation of a cloud computing service for finite element analysis[J]. Advances in Engineering Software, 2013, 60-61: 122-135.

[31] 符偉. 云計算環(huán)境下的線性有限元方法研究[D]. 武漢: 華中科技大學(xué), 2013.

[32] Zhang Y, Gallipoli D, Augarde C E. Simulation- based calibration of geotechnical parameters using parallel hybrid moving boundary particle swarm optimization[J]. Computers and Geotechnics, 2009, 36(4): 604-615.

[33] 張友良, 馮夏庭, 茹忠亮. 基于區(qū)域分解算法的巖土大規(guī)模高性能并行有限元系統(tǒng)研究[J]. 巖石力學(xué)與工程學(xué)報, 2004, 23 (21): 3636-3641.

Zhang Youliang,Feng Xiating, Ru Zhongliang. Large-scale high performance parallel finite element system based on domain decompositioin method in geomechanics[J]. Chinese Journal of Rock Mechanics and Engineering , 2004, 23(21): 3636-3641.

[34] Zhang Youliang, Domenico Gallipoli. Development of an object-oriented parallel finite element code for unsaturated soils[M]. Berlin Heidelberg: Springer, 2007.

[35] 金亮, 汪東梅, 邱運濤, 等. 基于彈性云計算集群的國際TEAM Problem 7基準(zhǔn)問題計算方法[J]. 電工技術(shù)學(xué)報, 2017, 32(8): 144-150.

Jin Liang, Wang Dongmei, Qiu Yuntao, et al. A calculation method for the international benchmark Problem of TEAM 7 based on elastic cluster in cloud computing[J]. Transactions of China Electrotechnical Society, 2017, 32(8): 144-150.

[36] 金亮, 邱運濤, 楊慶新, 等. 基于云計算的電磁問題并行計算方法[J]. 電工技術(shù)學(xué)報, 2016, 31(22): 5-11.

Jin Liang, Qiu Yuntao,Yang Qingxin, et al. A parallel computing method to electromagnetic problems based on cloud computing[J]. Transactions of China Electrotechnical Society, 2016, 31(22): 5-11.

[37] 顏威利, 楊慶新, 汪友華, 等. 電氣工程電磁場數(shù)值分析[M]. 北京：機械工業(yè)出版社, 2006.

[38] 張友良, 譚飛, 張禮仁, 等. 巖土工程億級單元有限元模型可擴展并行計算[J]. 巖土力學(xué), 2016, 37(11): 3309-3316.

Zhang Youliang, Tan Fei, Zhang Liren, et al. Scalable parallel computation for finite element model with hundreds of millions of elements in geotechnical engineering[J]. Rock and Soil Mechanics, 2016, 37(11): 3309-3316.

[39] Problem 7 asymmetrical conductor with a hole[DB/OL].https://www.compumag.org/wp/wp-content/uploads/2018/ 06/problem7.pdf.

Extensible Parallel Computing Method with Hundreds of Millions of Freedoms for Large-Scale Engineering Electromagnetic Field

Jin Liang1,2Li Yuzeng1,2YangQingxin1,2Zhang Chuang1,2Yan Shuai3

（1. State Key Laboratory of Reliability and Intelligence of Electrical Equipment Hebei University of Technology Tianjin 300130 China 2. Key Hebei Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability Hebei University of Technology Tianjin 300130 China 3. Institute of Electrical Engineering Chinese Academy of Sciences Beijing 100081 China）

Accurate and rapid electromagnetic field calculation is the basis of fine simulation and optimization design of electrical equipment. In this paper, the scalable parallel computing research is carried out on the elastic cluster of high-speed interconnected high-performance cloud platform. OpenMpi is used as the message passing library, and the dual-primal finite element tearing and interconnecting (FETI-DP) method is selected as the domain decomposition algorithm. The parallel computing of eddy current magnetic vector potentialwith constant conductivity is achieved by improving the master-slave/peer parallel program framework, which can reduce the complexity of programming and improve the efficiency of parallel computing. The program is written in C language and the scalable parallel computing method is verified by the benchmark problem of international TEAM Problem 7. In this paper, the master-slave/peer-to-peer parallel program framework and the dual-primal finite element tearing and interconnecting FETI-DP method are introduced into the field of electromagnetic computing, which improves the efficiency and scalability of parallel computing, and provides a new practical and theoretical method for large-scale engineering electromagnetic field calculation.

Parallel computing, numerical calculation of electromagnetic fields, finite element method, dual-primal finite element tearing and interconnecting(FETI-DP)

10.19595/j.cnki.1000-6753.tces.211050

TM153

國家自然科學(xué)基金面上項目（51977148）和國家自然科學(xué)基金重大研究計劃項目（92066206）資助。

2021-07-09

2021-11-01

金 亮 男，1982年生，博士，教授，研究方向為工程電磁場與磁技術(shù)、電磁場云計算和電磁無損檢測等。E-mail：jinliang@tju.edu.cn（通信作者）

李育增 男，1996年生，碩士研究生，研究方向為工程電磁場。E-mail：lyz18330774321@163.com

（編輯 郭麗軍）