基于有限單元和模型降階的儲能飛輪轉子動力學建模及分析

周傳迪， 柳亦兵， 朱萬程， 張昊隨

(1．華北電力大學 電站能量傳遞轉化與系統教育部重點實驗室，北京 102206；2．華北電力大學 先進飛輪儲能技術研究中心，北京 102206)

飛輪儲能系統(FESS)具有功率密度大、無污染和充放電速度快等優點，被廣泛應用于工程領域。飛輪儲能系統的充放電過程通過飛輪轉子的升降速實現，轉子工作轉速寬，但工作轉速范圍可能包括臨界轉速，導致振動問題突出[1]，因此有必要對飛輪轉子進行動力學建模和分析。

目前，飛輪轉子動力學建模方法主要包括有限元法、傳遞矩陣法及集中質量法。在有限元建模方面，唐長亮等[2-3]建立了飛輪轉子的有限元模型，對轉子的不平衡響應進行了分析，通過實驗驗證了計算結果的準確性。在集中質量建模方面，蔣書運等[4]建立了飛輪轉子的集中質量模型，采用拉格朗日法得到了轉子的運動微分方程并進行了動力學數值仿真。戴興建等[5]建立了飛輪轉子的集中質量模型，分析了飛輪轉子的動特性。Wang等[6]建立了四自由度飛輪-阻尼器的集中質量模型，采用拉格朗日法獲得了四自由度飛輪的動力學方程，采用有限元法求解擠壓油膜阻尼器動態特性的雷諾方程，將計算得到的不平衡響應與試驗結果進行對比。Qiu等[7]為100 kg級飛輪儲能系統研制了一種擺錘調諧質量阻尼器，利用拉格朗日定理建立了該系統的四自由度動力學模型，從理論和實驗上分析了系統的模態特性、臨界轉速和不平衡響應，并通過實驗驗證了擺錘調諧質量阻尼器抑制振動的有效性。上述2種建模方法中，有限元法可以得到比較準確的計算結果，但是其計算量較大、計算耗時長；集中質量法將飛輪等效為若干集中質量點，降低了飛輪轉子自由度，減少了計算量，但是未考慮轉子輪盤厚度的影響，導致分析結果存在誤差[8-9]。飛輪轉子的半徑和轉速增加受到材料強度限制，主要通過增加轉子輪盤厚度來增加儲能，采用集中質量法對轉子輪盤厚度較大的飛輪轉子進行動力學建模會影響計算結果的準確性。

筆者借鑒集總參數建模方法[10]，綜合有限單元法[11]和模型降階法[12]，考慮轉子輪盤厚度，提出一種適用于飛輪轉子的建模方法。首先依據集總參數法對飛輪轉子進行質量離散化，得到飛輪轉子-軸承系統的質量、阻尼和陀螺矩陣以及各軸段的抗彎剛度，然后利用有限單元法計算各軸段的剛度矩陣，再依據飛輪轉子剛體假設，采用模型降階轉換矩陣對模型進行簡化，得到最終的飛輪轉子-軸承系統模型。為驗證建模方法的適用性，筆者以飛輪轉子-軸承系統為對象，基于Jeffcott轉子集中質量建模方法、本文的建模方法以及有限元建模方法進行動特性計算，求解飛輪轉子在不同輪盤厚度下的固有頻率，對比3種建模方法的計算結果，以有限元模型計算結果作為基準，探究3種建模方法在不同轉子輪盤厚度情況下的計算誤差，并驗證本文建模方法的合理性。

1 飛輪儲能系統簡介

飛輪儲能系統本體部分的主要結構有徑向軸承、軸向磁軸承、飛輪轉子、電機轉子、雙向電機及飛輪外殼、抽真空與冷卻系統等組成，如圖1所示。

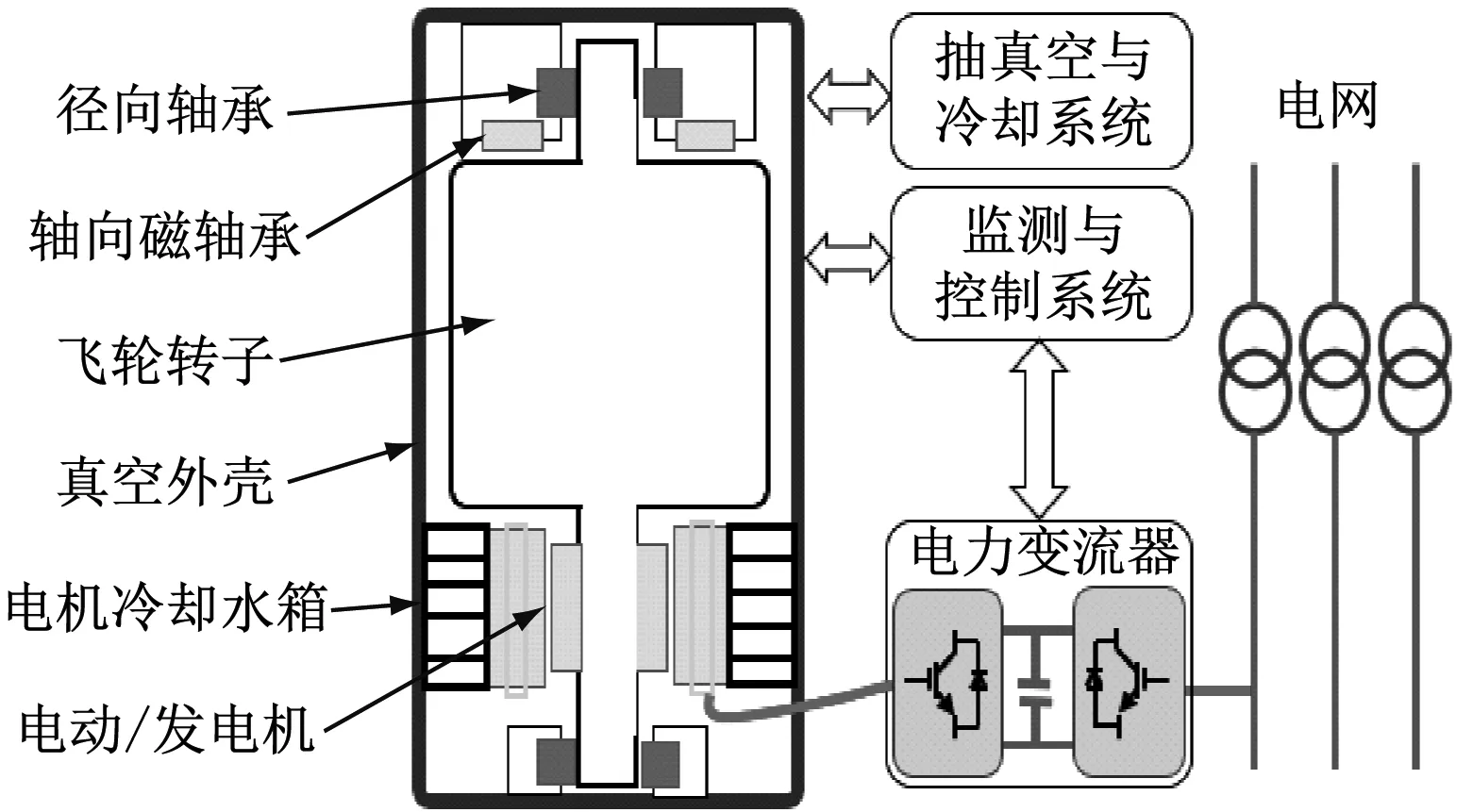
圖1 飛輪儲能系統簡化模型

飛輪儲能系統通過雙向電機對電能與動能進行轉換，做到能量的儲存和釋放。充電時，電能通過電機轉換為動能，帶動飛輪轉子進行升速，直到飛輪轉子達到最大工作轉速，電機停止驅動，完成充電過程。放電時，飛輪轉子的動能通過電機轉換為電能進行放電，飛輪轉子轉速降低，直到降至最小工作轉速，此時停止放電，飛輪轉子完成放電過程。

飛輪轉子-軸承系統是飛輪儲能系統的關鍵子系統之一，為了保證飛輪轉子安全穩定運行，有必要對飛輪轉子-軸承系統進行動力學建模和動特性分析。

2 飛輪轉子-軸承系統建模方法

2.1 基于有限單元法和模型降階法的飛輪轉子-軸承系統動力學建模

由圖1可知，飛輪轉子-軸承系統主要由轉軸、轉子輪盤、電機軸套和上下徑向軸承組成。為了方便理解筆者提出的基于有限單元法和模型降階法的飛輪轉子動力學建模方法，暫時不考慮電機軸套，對飛輪轉子-軸承系統進行簡化，如圖2所示，其中c1、c2分別為上、下軸承的阻尼，k1、k2分別為上、下軸承的剛度。

圖2 飛輪轉子-軸承系統簡化模型

飛輪轉子軸向由永磁軸承支撐，徑向由機械軸承支撐，建立動力學模型時不考慮轉子軸向振動，并將徑向軸承簡化為彈簧和阻尼系統。圖2中飛輪轉子可分為3個軸段：上軸段①，長度為L1；飛輪轉子輪盤②，長度為L2；下軸段③，長度為L3。假設飛輪轉子有5個節點(圖2中節點1～節點5)，上、下軸承分別位于節點1、節點4上。基于以上假設，對飛輪轉子進行動力學建模。

根據動力學相關理論，考慮陀螺效應的飛輪轉子-軸承系統運動方程的一般形式可以描述為：

(1)

式中：qu為自由度坐標；Mu、Cu、Gu和Ku分別為飛輪轉子-軸承系統的質量矩陣、阻尼矩陣、陀螺矩陣和剛度矩陣；Fu為系統所受到的外力和不平衡力；w為轉子轉速；Mx、My分別為x和y方向的質量；Cx、Cy分別為x和y方向的阻尼；Fux、Fuy分別為x和y方向的外力；qux、quy分別為x和y方向的位移；G、-GT分別為x和y方向的陀螺矩陣。

只要推導出上述各個矩陣的表達式，即可得到完整的飛輪轉子-軸承系統動力學方程。

首先，利用集總參數法對飛輪轉子進行離散化，如圖3所示。將圖2中的上軸段①、飛輪轉子輪盤軸段②和下軸段③分別標記為i=1、2、3軸段。圖3(a)給出了轉子的第i個軸段的集中質量模型，其中mi、Li、Jpi、Jdi、EiIi分別為第i個軸段的質量、軸段長度、極轉動慣量、赤道轉動慣量和抗彎剛度。

考慮轉子軸段的質量和剛度，依據質量不變和轉動慣量不變原則，將第i個軸段轉化為2個有慣性無剛度的集中質量點以及有剛度無質量的彈性軸組成的模型，如圖3(b)所示。其中，mi,u、Jpi,u、Jdi,u分別為第i個軸段集中在第i個質量點上的質量、極轉動慣量和赤道轉動慣量；mi,d、Jpi,d、Jdi,d分別為第i個軸段集中在第i+1個質量點上的質量、極轉動慣量和赤道轉動慣量。計算公式如下：

(2)

(a) (b)

圖2中的轉子模型有3個軸段，因此可得到4個集中質量點，將各個軸段集中在各個質量點處的參數相加，可以得到各個質量點處的集總質量和轉動慣量。

(3)

不考慮轉軸內阻尼，可以得到飛輪轉子-軸承系統的質量矩陣Mu、阻尼矩陣Cu和陀螺矩陣Gu的表達式：

(4)

式中：xi為x方向各節點位移；yi為y方向各節點位移；θxi和θyi為轉角。

式(4)忽略了自由度θy1、θy4、θx1和θx4，這是因為本文所用軸承為短軸承約束，該轉動自由度可由其他自由度表示。

為考慮轉子各個軸段的剛度對飛輪轉子-軸承系統動特性的影響，采用有限元法，以軸段作為單個單元求解其剛度矩陣。飛輪轉子輪盤②可視為無分布力、無約束的梁單元，如圖4所示，其中L為梁單元長度，EI為抗彎剛度，M1、M2為兩端點的扭矩，F1、F2為兩端點的力。上軸段①和下軸段③可視為具有短軸承約束的梁單元，如圖5所示，其中kb為軸承約束剛度。

圖4 無分布力、無約束梁單元

圖5 短軸承支撐梁單元

對于圖4所示的無分布力、無約束的梁單元，可根據文獻[13]得到其剛度矩陣方程：

(5)

對于圖5所示的短軸承支撐的梁單元，可將軸承等效為彈簧剛度[13]，且沒有支撐力矩M。因此，短軸承支撐梁單元具有以下邊界約束：

(6)

將式(6)代入式(5)可得：

6L·x1+2L2·θy1-6L·x2+4L2·θy2=M2=0

(7)

由于M2=0，自由度θy2可由x1、θy1、x2表示：

(8)

為方便分析，對式(5)進行矩陣分塊可得：

(9)

將式(9)化為方程組形式：

(10)

對式(10)中第2個公式進行分析，得到Uu2與Uu1的關系式：

(11)

(12)

由此得到下軸段③的剛度矩陣方程為：

(13)

依據F2=-kbx2，將彈簧納入梁單元中可得：

(14)

綜上，上軸段①、飛輪轉子輪盤②和下軸段③的剛度矩陣分別為：

(15)

式中：kb1、kb2為上、下軸承約束剛度；I1～I3為3個軸段的轉動慣量。

將3個軸段的剛度矩陣置于相應的節點位置并按照有限元法組合得到飛輪轉子-軸承系統的剛度矩陣：

(16)

其中，

觀察圖2轉子模型發現，飛輪轉子輪盤②的直徑與上軸段①和下軸段③的直徑相差較大，節點2與節點3之間的剛度較大。為了簡化方程，將飛輪轉子輪盤②視為剛體，用節點5代替節點2和節點3。假設飛輪轉子輪盤②中心節點5的自由度坐標為(x5，y5，θx5，θy5)，依據剛體和小位移假設，得到圖2中節點2的自由度(x2，y2，θx2，θy2)和節點3的自由度(x3，y3，θx3，θy3)與(x5，y5，θx5，θy5)的關系：

(17)

式中：Lz1和Lz2分別為節點5與節點2和節點3的距離。

根據式(17)，矩陣E1和E2存在以下關系：

(18)

根據式(18)可得：

ETqub=0

(19)

假設存在模型轉換矩陣T滿足下式：

qub=Tqr

(20)

其中，qr=[x1x5θy5x4]T。

將式(20)代入式(19)可得：

ETqub=ETTqr=0

(21)

由于qr不為零，可得：

ETT=0

(22)

根據文獻[13]得到模型轉換矩陣T還應該滿足矩陣Y1為非奇異矩陣條件：

(23)

經計算得到的模型轉換矩陣為：

(24)

其中，

利用模型轉換矩陣T對式(1)所示的模型進行模型簡化后得到飛輪轉子-軸承系統的運動方程：

(25)

其中，M=TTMuT,G=TTGuT,C=TTCuT,K=TTKuT,F=TTFu,q=[x1x5θy5x4y1y5θx5y4]T。

2.2 基于Jeffcott轉子的集中質量模型

在轉子動力學建模方面，基于Jeffcott轉子模型的集中質量法應用較為廣泛[14-15]。Jeffcott轉子模型適用于轉子動特性的定性分析，在定量分析方面，其對具有薄輪盤的轉子建模誤差不大，但是針對儲能飛輪轉子此類具有厚輪盤的轉子，其建模誤差較大。

為了探究基于Jeffcott轉子模型的飛輪轉子在不同輪盤厚度下的建模誤差，基于Jeffcott轉子模型對飛輪轉子進行動力學建模，探討其建模誤差來源，為下文基于該模型的飛輪轉子動特性計算和誤差對比提供理論參考，僅作為后續章節不同模型之間的計算誤差對比之用。

根據Jeffcott轉子模型的簡化假設，將上軸段①和下軸段③視為有彈性無質量軸，飛輪轉子輪盤②簡化為一個質量集中在節點5處的圓盤，只考慮飛輪轉子的平動自由度(x5，y5)和轉動自由度(θx5，θy5)，根據達朗貝爾原理，采用Jeffcott轉子模型建立的考慮陀螺效應的飛輪轉子-軸承系統的動力學方程[22]如下：

(26)

式中：m為飛輪轉子輪盤②的質量；Jd為轉子赤道轉動慣量；Jp為轉子極轉動慣量。

式(26)中各個剛度項的計算公式如下：

(27)

式中：a、b分別為飛輪轉子中心節點5與上、下軸承的距離。

綜上所述，方程式(26)的剛度項來自于軸承彈簧剛度以及上軸段①和下軸段③的抗彎剛度，質量項主要來自飛輪轉子輪盤②的質量。因此，Jeffcott轉子模型的主要誤差來源于忽略轉軸質量和忽略轉子輪盤厚度產生的剛度影響。

3 建模方法驗證

為了探究各建模方法在不同轉子輪盤厚度下的誤差，對基于Jeffcott轉子模型、本文模型及有限元模型建立的飛輪轉子動力學模型進行變轉子輪盤厚度的固有頻率計算，以有限元模型的計算結果作為基準對其他2種模型進行誤差分析。

對于實際的飛輪轉子系統而言，大多數飛輪轉子在轉軸上嵌套有電機轉子。考慮電機轉子質量和附加剛度的影響，建立了如圖6所示的飛輪轉子-電機轉子-軸承系統模型，并計算了在不同轉子輪盤厚度下的前兩階固有頻率，其中轉子輪盤厚度變化范圍為25～300 mm，在轉子輪盤直徑一定的情況下，對應的轉子輪盤厚度與直徑比為0.08～1，其他參數見表1。

圖6 飛輪轉子-電機轉子-軸承系統模型

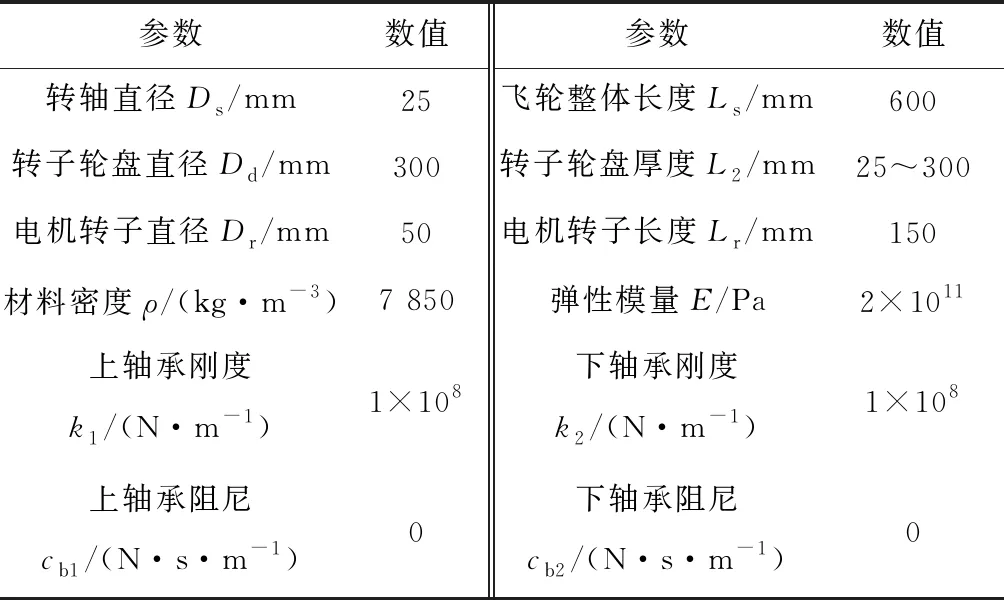
表1 飛輪轉子-電機轉子-軸承系統參數

飛輪轉子-電機轉子-軸承系統的前兩階固有頻率隨轉子輪盤厚度變化曲線如圖7所示。對于一階固有頻率，隨著轉子輪盤厚度增加，本文模型與有限元模型計算結果均呈先減小后增大的趨勢，Jeffcott轉子模型的計算結果一直呈減小趨勢。當轉子輪盤厚度較小時，本文模型與有限元模型計算結果有一定誤差，隨著轉子輪盤厚度增加，相對誤差逐漸減小。Jeffcott轉子模型的計算結果在轉子輪盤厚度較小時與有限元模型計算結果接近，隨著轉子輪盤厚度增加，相對誤差逐漸增大。

(a) 一階固有頻率

(b) 二階固有頻率

對于二階固有頻率，隨著轉子輪盤厚度增加，本文模型與有限元模型計算結果均呈先減小后增大的趨勢，Jeffcott轉子模型的計算結果一直呈減小趨勢。本文模型的計算結果與有限元模型計算結果吻合，當轉子輪盤厚度增加至一定值時開始略有差別。Jeffcott轉子模型的計算結果與有限元模型計算結果在轉子輪盤厚度較小時較為接近，隨著轉子輪盤厚度增加，兩者的相對誤差逐漸增大。

Jeffcott轉子模型的固有頻率ωd與剛度、質量的關系為：

(28)

式中：ks為轉子的軸段及支撐的串聯剛度；ms為轉子的質量，由于Jeffcott轉子模型不考慮轉子厚度，因此其剛度不隨轉子輪盤厚度變化而變化，而轉子質量隨著轉子輪盤厚度的增加而增大，從而導致轉子的固有頻率隨轉子輪盤厚度的增加一直呈減小趨勢。

圖8為不同轉子輪盤厚度下，基于本文模型和Jeffcott轉子模型計算得出的飛輪轉子-電機轉子-軸承系統的前兩階固有頻率與有限元模型計算結果的相對誤差。從圖8可以看出，對于一階固有頻率，Jeffcott轉子模型的計算結果在轉子輪盤厚度較小時相對誤差小，轉子輪盤厚度為0.03 m時，相對誤差為0.28%，隨著轉子輪盤厚度的增加，相對誤差一直增大，當轉子輪盤厚度增加至0.3 m時，相對誤差達到最大值55.78%。轉子輪盤厚度為0.25 m時，本文模型計算結果的相對誤差達到最大值6.24%，隨著轉子輪盤厚度增加，相對誤差逐漸降低，在轉子輪盤厚度為0.165 m時相對誤差達到最小值0.014%，之后隨著轉子輪盤厚度進一步增加，相對誤差開始逐漸增大，轉子輪盤厚度為0.285 m時相對誤差增大至2.97%。

(a) 一階固有頻率相對誤差

(b) 二階固有頻率相對誤差

對于二階固有頻率，Jeffcott轉子模型的計算結果相對誤差隨轉子輪盤厚度增加而增大，轉子輪盤厚度為0.3 m時，相對誤差達到最大值79.77%。本文模型的計算結果相對誤差一直較小，轉子輪盤厚度為0.3 m時，相對誤差達到最大值2.89%。

圖9給出了不同轉子輪盤厚度與直徑比情況下，本文模型和Jeffcott轉子模型計算得出的飛輪轉子-電機轉子-軸承系統的前兩階固有頻率與有限元模型計算結果的相對誤差。從圖9可以看出，基于Jeffcott轉子模型的飛輪轉子在轉子輪盤厚度與直徑比為0.08～0.23時，其一階固有頻率相對誤差在10%以下；轉子輪盤厚度與直徑比為0.08～0.12時，二階固有頻率相對誤差在10%以下；轉子輪盤厚度與直徑比為>0.23～1時，相對誤差均在10%以上，因此Jeffcott轉子模型不適于厚輪盤飛輪轉子的動力學建模和動特性計算。

圖9 飛輪轉子-電機轉子-軸承系統的前兩階固有頻率相對誤差隨轉子輪盤厚度與直徑比的變化

對于本文模型，轉子輪盤厚度與直徑比為0.35～0.73時，相對誤差不超過1%，轉子輪盤厚度與直徑比在0.08～<0.35、>0.73～1內總體相對誤差也較小，最大不超過6.24%，比較適用于厚輪盤飛輪轉子的動力學建模和動特性計算。

4 結 論

(1) 當轉子輪盤厚度較小，轉子輪盤厚度與直徑比為0.08～0.23時，3種建模方法計算得到的固有頻率相差較小，總體上本文模型與有限元模型的計算結果更為接近。當轉子輪盤厚度逐漸增加，轉子輪盤厚度與直徑比大于0.23時，Jeffcott轉子模型的計算結果與有限元模型計算結果的相對誤差已超過10%，而本文模型的計算結果則始終與有限元模型計算結果比較吻合，相對誤差一直較小，轉子輪盤厚度與直徑比為0.35～0.73時相對誤差最小。

(2) 采用Jeffcott轉子模型對轉子輪盤厚度與直徑比較大的飛輪轉子進行動力學建模時相對誤差偏大，本文的建模方法對于具有較大輪盤厚度與直徑比的飛輪轉子動力學建模有較好的適用性。