一維彈性碰撞二級結論的幾種推導方法及應用
董廷燦
(安徽省明光中學)
碰撞問題是高中物理中的典型問題,其中一維彈性碰撞問題一直是高考的熱點,這類問題所涉及的數學運算往往比較麻煩,但是若能夠活用一維彈性碰撞的二級結論,特別是掌握其推導方法,將大大提高解題的速度.
1 一維彈性碰撞的二級結論
如圖1所示,兩個質量分別為m1、m2,大小相同的剛性小球分別以速度v10、v20在光滑的水平面上沿同一直線運動,若它們能發生碰撞(為一維彈性碰撞),碰撞后它們的速度分別是v1、v2,以地面為參考系,將兩個小球看作系統,在碰撞過程中由動量守恒定律及機械能守恒定律得
圖1
聯立①、②兩式解得
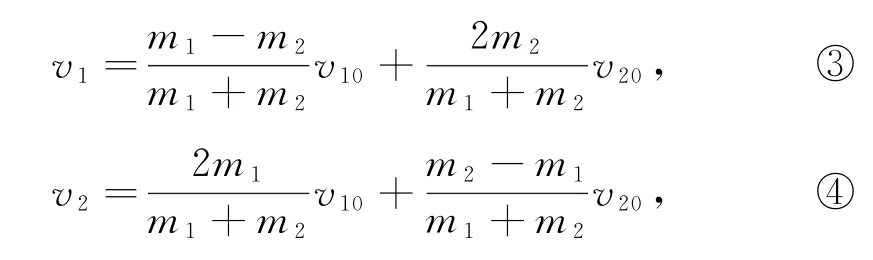
式③、式④即為一維彈性碰撞普適公式常用的二級結論,很多教師會讓學生記住結論便于求解.
在一維一動碰一靜的彈性碰撞中,可以令v10=v0,v20=0,整理得
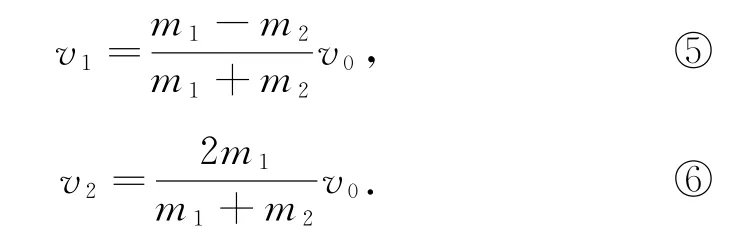
當m1>m2時,解得v1>0,v2>0;
當m1=m2時,解得v1=0,v2=v0;
當m1<m2時,解得v1<0,v2>0.
即“大碰小,一起跑;小碰大,要反彈;質量相等,速度交換”.
以上二級結論在高考和平時模擬中的應用是比較廣泛的,那么應該如何推導呢?
2 5種推導方法
2.1 因式分解法
由式①、式②移項可得

式⑧進一步整理得
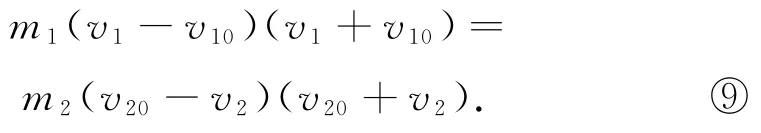
將⑦⑨兩式左右相比,可得
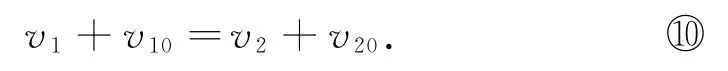
聯立⑦⑩兩式解得
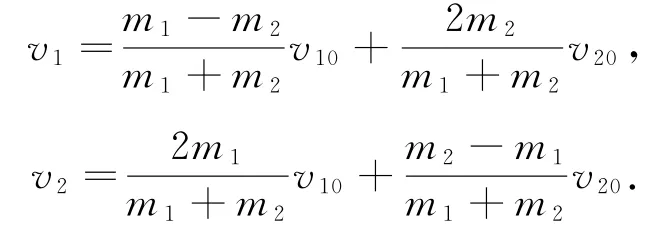
2.2 求根公式法
由式①得
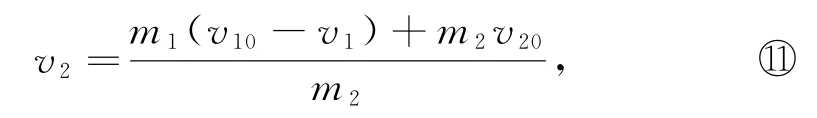
代入式②得
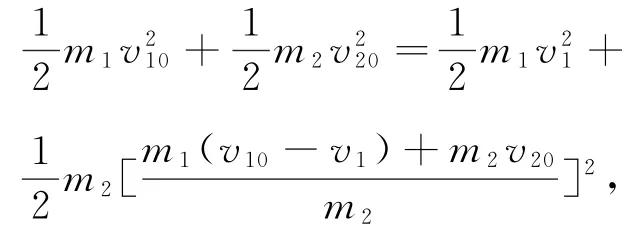
整理得
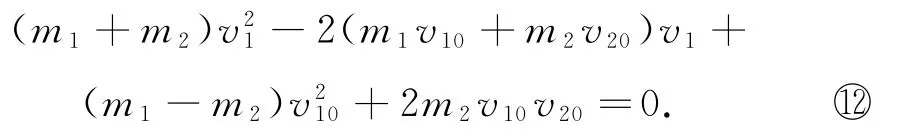
代入求根公式得
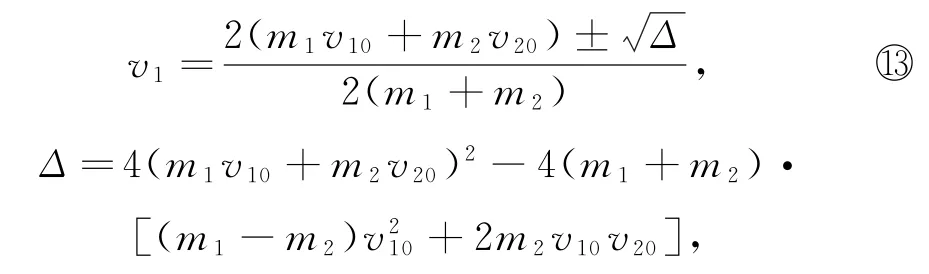
整理得
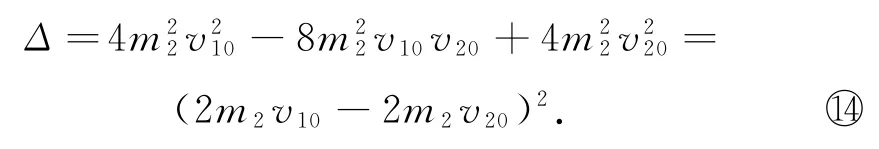
代入式?得
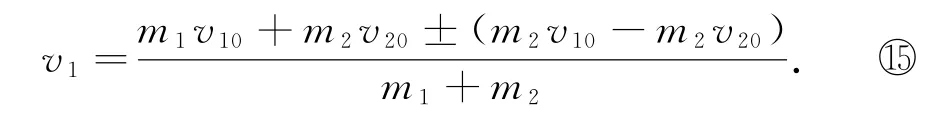
考慮到碰撞之后兩物體的速度一定會改變,式?中只有一個解是符合要求的,即
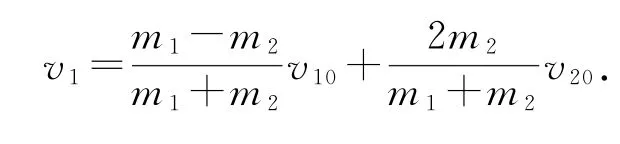
2.3 參考系法
假設將兩個質量分別為m1、m2大小相同的剛性小球,置于以速度v20水平向右勻速運動的慣性系內,則在該慣性系中,小球m1的速度為v10-v20,小球m2的速度為0,這就相當于以地面為參考系的一維一動碰一靜的彈性碰撞,代入式⑤、式⑥得

再以地面為參考系,對式?、式?整理可得
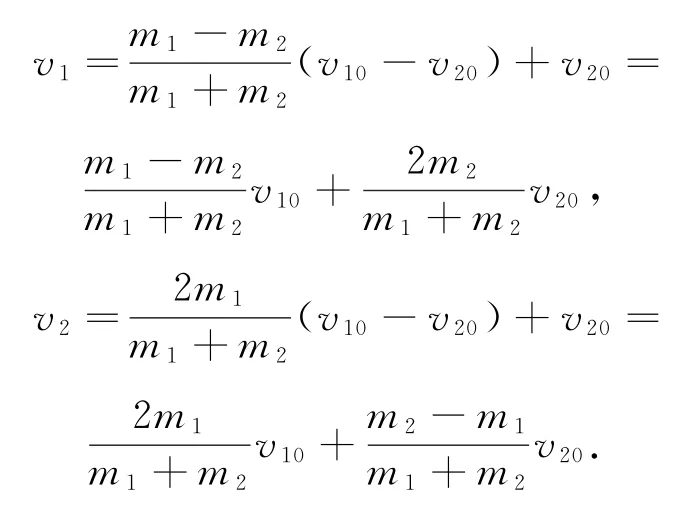
2.4 恢復系數法
1)恢復系數
恢復系數是反映碰撞時物體形變恢復能力的參數,它只與碰撞物體的材料性質有關,其定義為兩物體碰撞后的分離速度(v2-v1)與碰撞前的接近速度(v10-v20)之比,如圖2所示,即

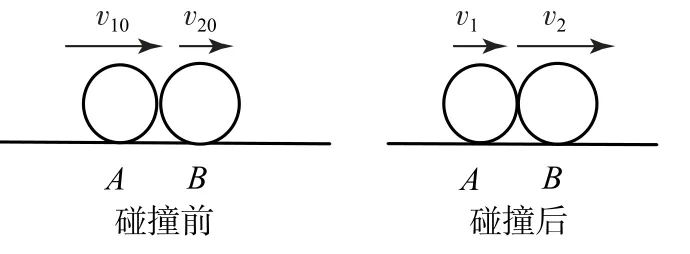
圖2
e是一個由實驗測定的常數,恢復系數的取值如下:發生彈性碰撞時e=1;非彈性碰撞時0≤e<1;完全非彈性碰撞時e=0.
2)推導過程
把式?代入式①得
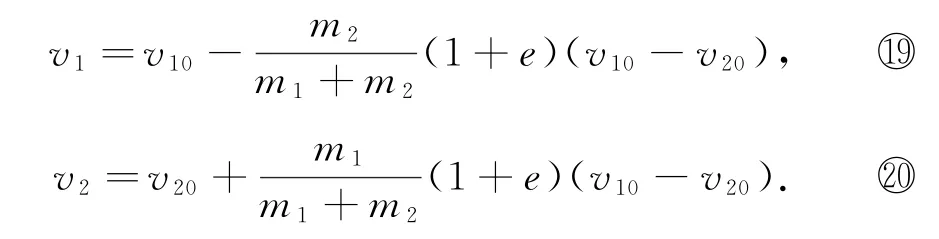
由式⑩可得發生彈性碰撞時v1+v10=v2+v20,整理得v10-v20=v2-v1,代入式?得恢復系數e=再代入??兩式整理得
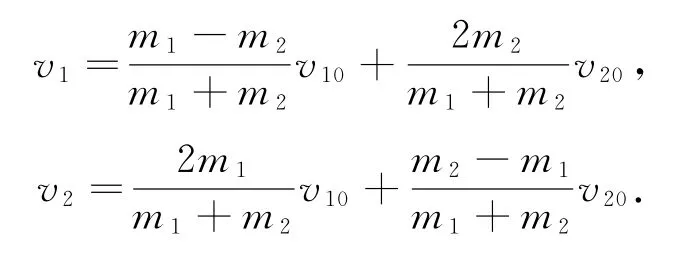
2.5 質心系法
質心是描述質點系整體運動狀態的代表點,是系統中位置矢量關于質量的加權平均值.定義質點系的質心參考系(或質心系)為原點固定在質心上且沒有轉動的參考系(平動參考系).
在質心參考系中,兩小球的總動量始終為零,而對于彈性碰撞,兩小球碰撞前后相對質心的速度大小不變,方向相反.由于兩小球系統所受合力為零,且系統總動量守恒,故系統質心的速度vC(質心相對于實驗室系的速度等于各質點動量之和與質心系各質點總質量的比值)不變,根據動量守恒定律可得
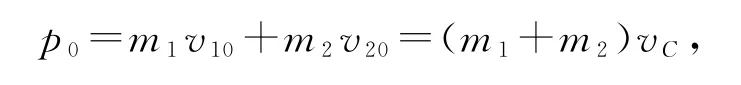
碰撞前,小球A相對質心的速度為v相對1=v10-vC.碰撞后,小球A相對質心的速度為v′相對1=v1-vC.因為v′相對1=-v相對1,即v1-vC=vC-v10,解得
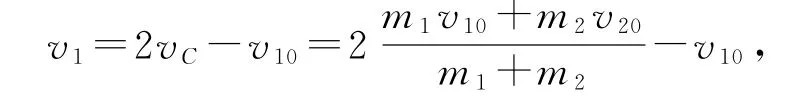
同理,亦可得碰撞后小球B的速度為
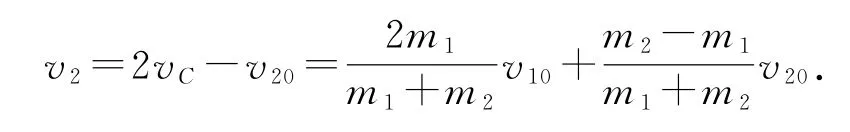
3 學以致用
例1 如圖1所示,A、B兩球大小相同,質量分別為m1、m2,分別以速度3v0、v0在光滑的水平面上沿同一方向做勻速直線運動,某一時刻兩球發生了彈性碰撞,碰后它們的速度分別為v1、v2,以兩球初速度方向為正方向,則下列說法正確的是( ).
A.若m1>m2,碰后A、B兩球的速度方向不變
B.若m1=m2,碰后v1=v0,v2=3v0
C.若m1<m2,碰后A球反彈,B球仍沿原方向運動
D.碰撞后兩球速度必滿足v2-v1=2v0
解析
把v10=3v0和v20=v0分別代入③④兩式整理得
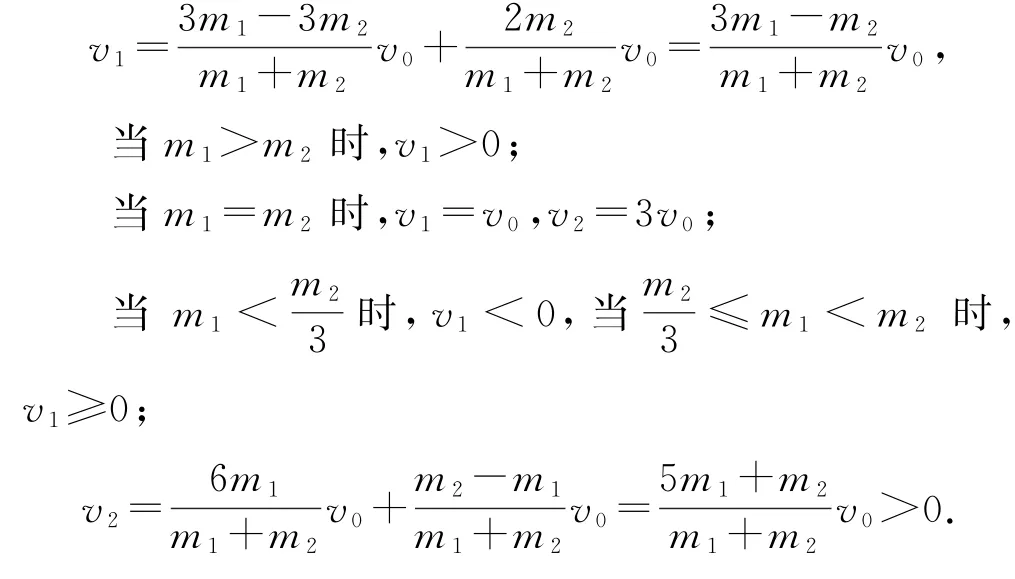
所以選項A、B正確,C錯誤.
由于兩球碰撞是一維彈性碰撞,把v10=3v0,v20=v0分別代入進一步整理得v2-v1=2v0,所以選項D正確.
例2如圖3所示,某科技興趣小組為了設計一種發射火箭的方案,選擇了兩個質量分別為m1和m2的彈性小球A、B疊放在一起,從高度為h處自由落下,高度h遠大于兩小球半徑,所有的碰撞都是完全彈性碰撞,且都發生在豎直方向.已知m2=7m1,則小球m1反彈后能達到的高度為( ).
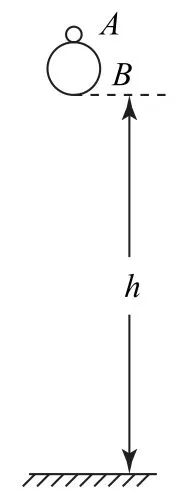
圖3
A.hB.3.5h
C.6.25hD.7h
解析
方法1(二級結論法) 下降過程為自由落體運動,觸地時兩球速度相同,由自由落體運動公式可得碰撞地面之后,速度瞬間反向,大小相等,選m1與m2碰撞過程為研究過程,碰撞前后動量守恒,設碰后m1、m2速度大小分別為v1、v2,選向上方向為正方向,則
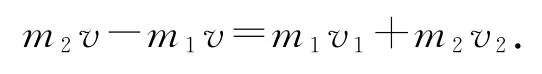
由能量守恒定律得
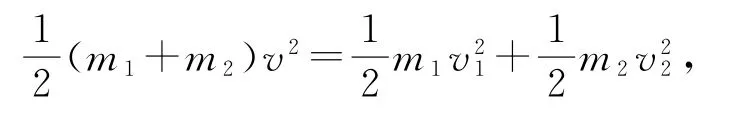
且m2=7m1,聯立解得
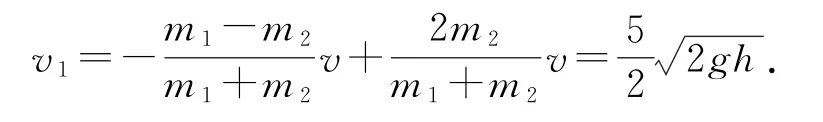
反彈后高度為H=6.25h.
方法2(質心系法) 設兩小球碰撞過程中的質心速度為vC.由動量守恒定律得
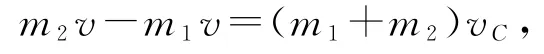
解得
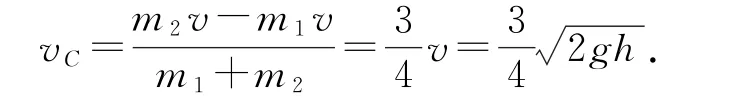
所以碰后A球的速度為
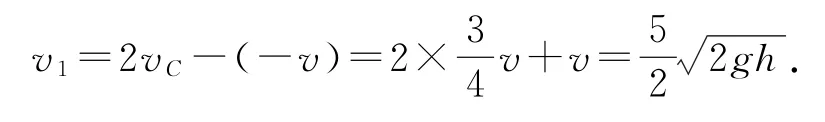
反彈后高度為H=6.25h.
例3 (2021年湖南卷)如圖4所示,豎直平面內一條足夠長的光滑傾斜軌道與一長為L的水平軌道通過一小段光滑圓弧平滑連接,水平軌道右下方有一段弧形軌道PQ.質量為m的小物塊A與水平軌道間的動摩擦因數為μ,以水平軌道末端O點為坐標原點建立平面直角坐標系xOy,x軸的正方向水平向右,y軸的正方向豎直向下,弧形軌道P端坐標為(2μL,μL),Q端在y軸上.重力加速度為g.
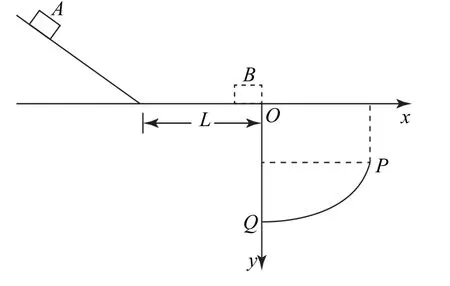
圖4
(1)若A從傾斜軌道上距x軸豎直高度為2μL的位置由靜止開始下滑,求A經過O點時的速度大小;
(2)若A從傾斜軌道上不同位置由靜止開始下滑,經過O點落在弧形軌道PQ上的動能均相同,求PQ的曲線方程;
(3)將質量為λm(λ為常數且λ≥5)的小物塊B置于O點,A沿傾斜軌道由靜止開始下滑,與B發生彈性碰撞(碰撞時間極短),要使A和B均能落在弧形軌道上,且A落在B落點的右側,求A下滑的初始位置距x軸高度的取值范圍.
解析
(1)A沿傾斜軌道由靜止開始下滑到O點的過程中,由動能定理得
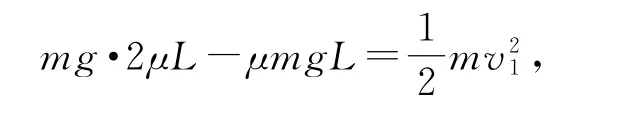
解得
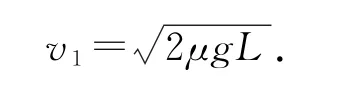
(2)假設A落到P點,結合平拋運動規律可得
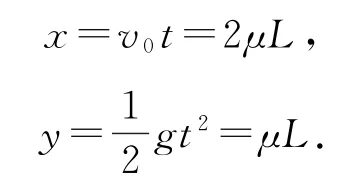
解得
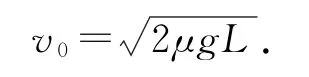
則落到軌道上時的動能
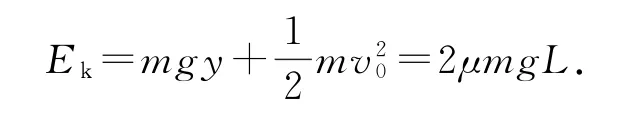
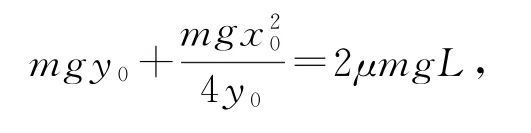
變形得
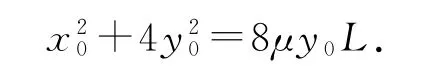
當x0=0時,y0=2μL,則PQ的曲線方程為
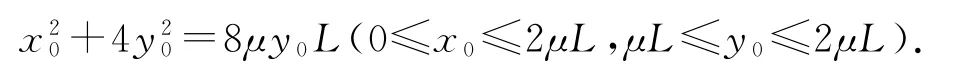
(3)令A碰撞前速度為v,釋放高度為h,由動能定理得
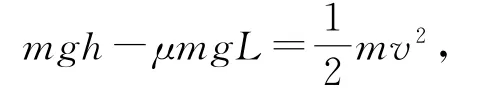
A、B發生彈性碰撞,碰撞過程中系統動量守恒,機械能守恒,設碰撞后A速度為vA,B速度為vB,可得
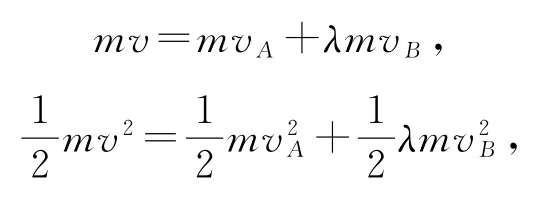
由λ≥5可知vA<0,即A碰后反彈,速度大小為
根據題意,為保證B落在軌道上,則vB≤v0=,即
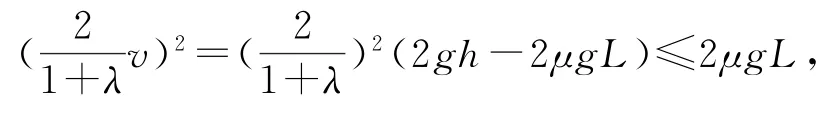
解得
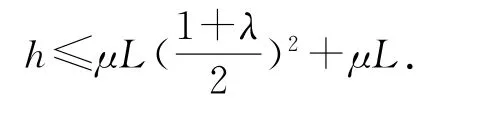
A反彈后,經歷一次往返后從O點拋出,拋出的速度為v2,由動能定理得
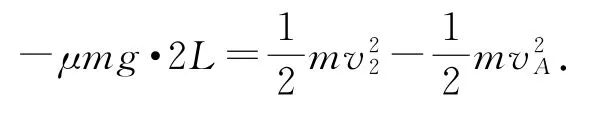
為保證A落在軌道上,則,即
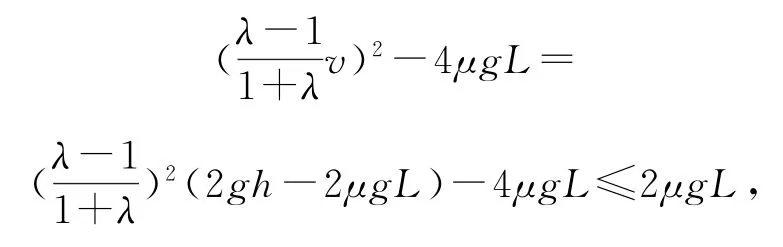
解得
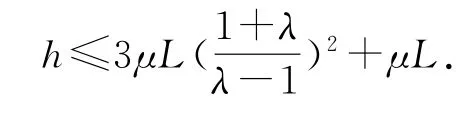
又為保證A落點在B右側,則v2>vB.
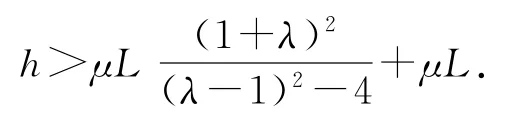
因為λ≥5,則μL小.
則釋放高度的取值范圍為
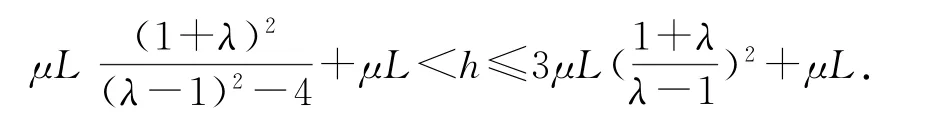
點評
由例1可知“大碰小,一起跑)小碰大,要反彈)質量相等,速度交換”的二級結論不是對任意的一維彈性碰撞都是成立的,它的適用條件是一維一動碰一靜的彈性碰撞,所以掌握結論的推導過程,進而理解其適用條件比只記結論更為重要.同時,合理地掌握一些二級結論,如例1中利用一維彈性碰撞恢復系數e=1,即兩物體碰撞后的分離速度等于碰撞前的接近速度)例2中利用質心速度vC=,且碰后A、B兩球的速度分別為v1=2vC-v10、v2=2vC-v20)例3中利用一動碰一靜的特殊情況下的二級結論,可以提高解題的效率.

