高中物理質能方程相關問題釋疑

周 凱

（深圳實驗學校光明部）

高中物理教材關于質能方程的介紹是十分簡潔的，人教版2007年版《選修3－4》“狹義相對論的其他結論”一節中對其的描述如下：相對論另一個重要結論就是大家都很熟悉的愛因斯坦質能方程E＝mc2.式中m是物體的質量，E是它具有的能量.人教社2019年版教材對相對論的內容進行了整合，質能方程只是出現在《選擇性必修三》“核力與結合能”一節“質量虧損”描述中，并且只是將其描述為“愛因斯坦已經給我們指出了物體的能量與它的質量的關系”，未明確稱之為質能方程.可見，兩版教材都只是直接給出質能方程的數學形式，并沒有對其具體含義進行深入解釋.筆者在聽課及教學中發現學生及部分教師關于質能方程的理解存在以下問題：(1)質能方程中的“能量”指的是物體的哪種能?(2)與之前學習的機械能、電勢能、內能等相比，這是一種新的形式的能量嗎?(3)今后再用能量觀點解決問題時，要不要考慮這種能量?要深入理解以上問題，需要借助相對論的有關知識.本文將從相對論的角度對這3個問題予以解釋.

1 相對論的質點動能公式

牛頓力學中將力定義為動量對時間的變化率，我們將其直接關聯到相對論中，可得

其中

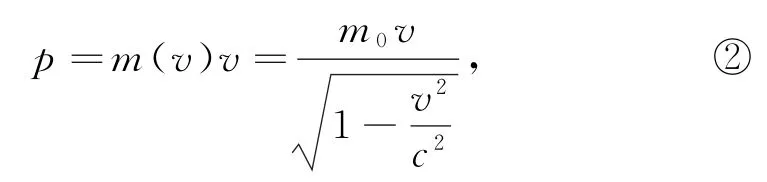
式②中c為光速，m0為質點的靜質量，m為質點的相對論質量，它是速率v的函數.

我們假定在相對論中，功能關系仍具有牛頓力學中的形式，質點的動能等于外力使它從靜止狀態開始運動所做的功，即

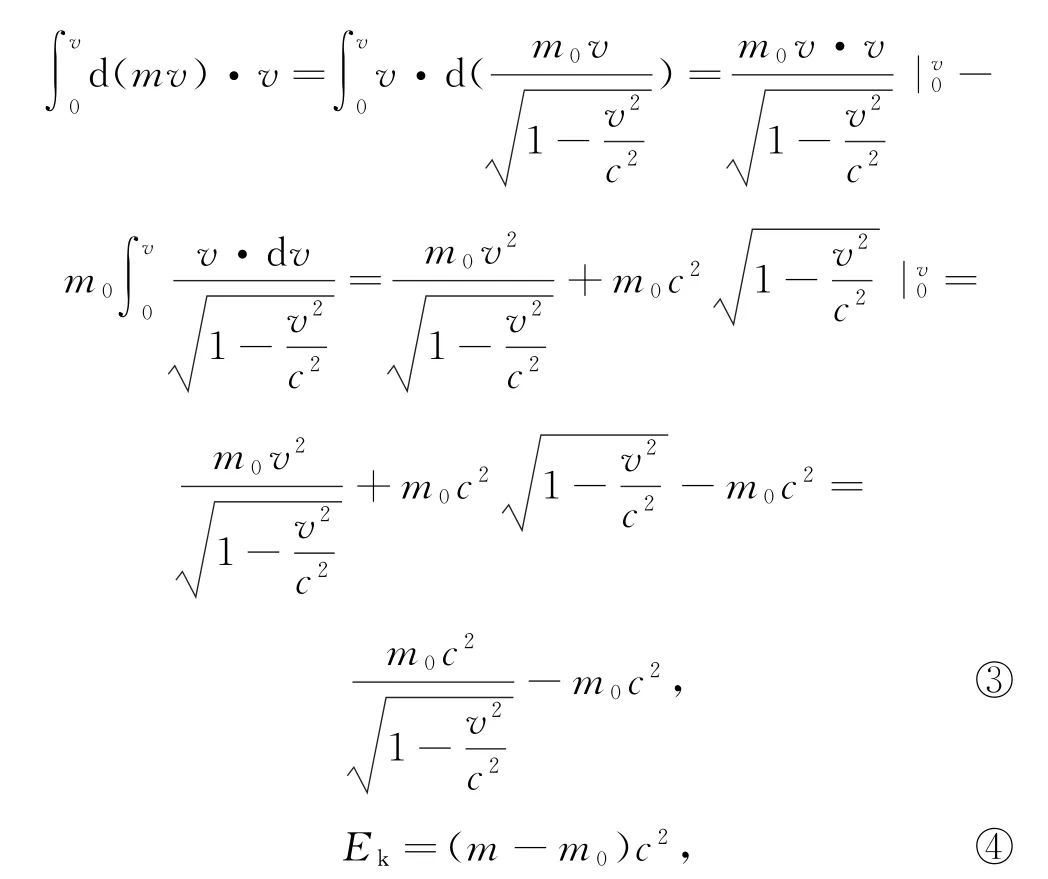
式④就是相對論的質點動能公式.質點的動能等于因運動而引起的質量的增量Δm＝m－m0與光速平方的乘積.

在非相對論近似下，v?c，我們可以對式③進行級數展開，忽略v的高次項，可得

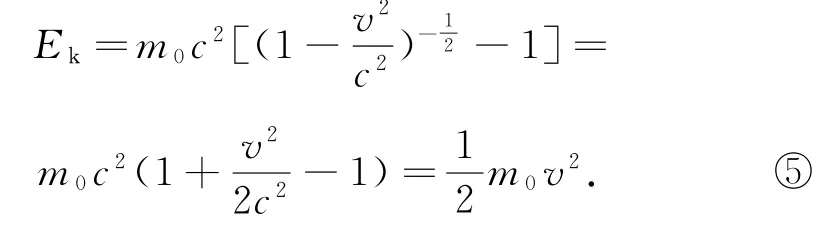
這樣相對論動能公式就簡化為經典動能公式.

2 質能方程

我們對相對論動能公式式④移項后得

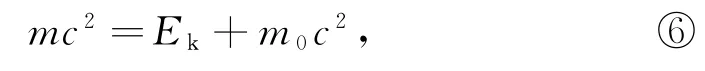
式⑥等號右邊第二項可以理解為質點靜止時所具有的能量，稱為靜能量，用符號E0表示，即

式⑥等號左邊mc2為物體的動能和靜能量之和，稱為物體總能量，用符號E表示，即

式⑧稱為質能關系或質能方程.質能方程是相對論動力學的一個重要結論，它揭示了物質的兩個基本屬性(質量與能量)之間的聯系和對應關系.

3 對相關問題的解釋

由質能方程可知，當物體靜止時，內部仍有復雜的運動，仍然具有m0c2的巨大能量.所以相對論能量mc2并不是經典力學中的動能或機械能，而是包含了物體全部能量(機械能、電磁能、熱能、光能、原子和分子的動能和勢能以及原子核能等)在內的總能量.這樣就回答了前文中的(1)(2)兩個問題.

對于問題(3)，今后再用能量觀點解決問題時，要不要考慮物體的靜能量或總能量?高中階段對于相對論的知識要求較低，學生遇到的絕大多數問題都是非相對論情況下的，運用牛頓力學即可解決.我們在用能量觀點解決問題時，還是按照經典力學的方法，考慮物體的機械能、電勢能、內能等即可，不必考慮能量mc2.可能有學生要問，需要考慮式⑦中物體的靜能量嗎?在非相對論情況下，對能量附加一個常量是沒有意義的，故無須加上靜能量.然而在相對論情形中，我們必須考慮物體的靜能量，因為這一項的出現是相對論協變性要求的結果.