非等時距灰色模型在建筑物沉降預測中的應用*
崔 偉,張緒濤,阮興群,孟凡濤
(1.聊城大學建筑工程學院,山東 聊城 252000;2.山東華科規劃建筑設計有限公司,山東 聊城 252000)
0 引言
沉降監測和預測是保證建筑物安全質量的重要方式[1-3]。當今我國城市化建設快速推進,尤其是高層建筑拔地而起,但是隨著建筑物高度不斷增加、荷載不斷加大以及監測預測分析未能及時跟進,造成了大量工程事故[4]。為此把握地基沉降發展規律并進行沉降預測有非常重要的意義[5]。國內學者對于建筑物沉降預測進行了大量研究:陳威等[6]將三點法與灰色模型(grey model,GM)相組合進行路基沉降預測,結果表明該方法可較好地用于路基沉降預測;姜獻東等[7]將灰色系統理論應用于軟基沉降預測;單瑞等[8]通過牛頓插值平均法與泊松曲線相結合的方式應用于高層建筑沉降預測中,結果表明泊松曲線預測與實際沉降預測曲線吻合性較好,擬合精度較高;劉光秀等[9]通過建立灰色-Gompertz組合模型,對高速公路軟土路基進行沉降預測分析,取得了良好效果。但是,目前建立的建筑物沉降預測模型大多算法繁雜不易實現,進而影響工程實際應用。
為提高預測模型的序列應用性和預測結果的可靠性,滿足工程實際應用,引入組合思維,根據聊城市昌潤祥荷園8號樓實測數據,通過三次樣條插值和灰色模型相結合,建立起非等時距灰色模型,將實測數據與預測數據對比分析,驗證本文方法的可行性,并采用控制變量法,對時間間隔和觀測次數兩種因素進行了精度分析,為構建高精度預測模型提供借鑒。
1 非等時距灰色模型
1.1 三次樣條插值法下的等時距數據轉化
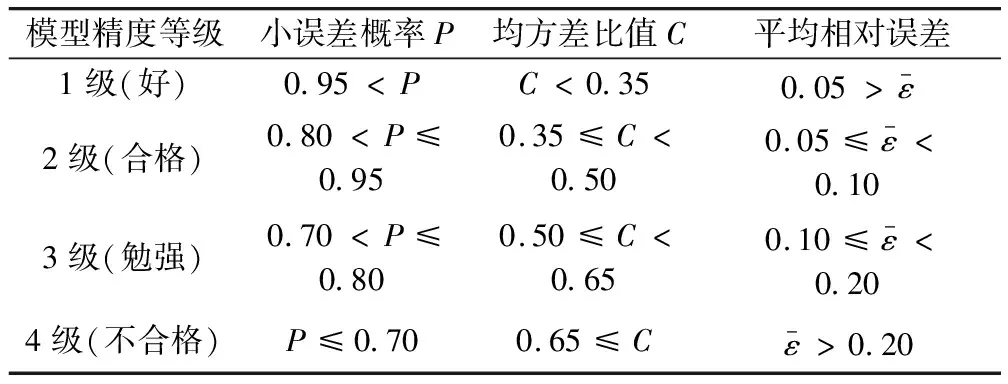
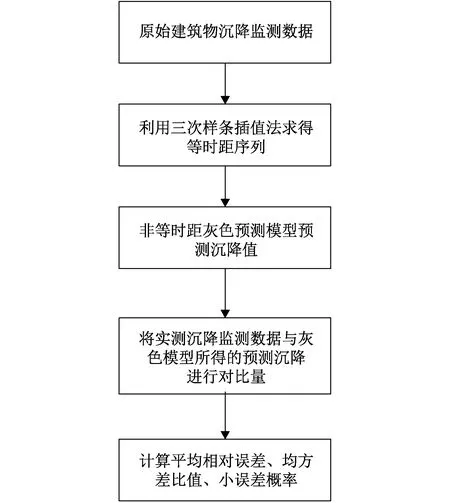
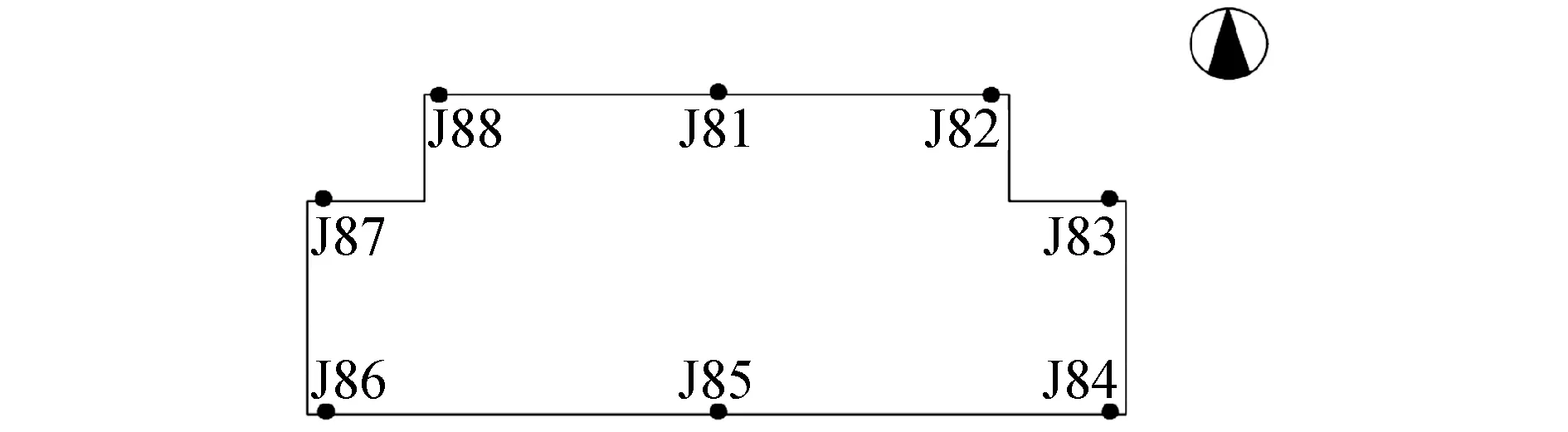
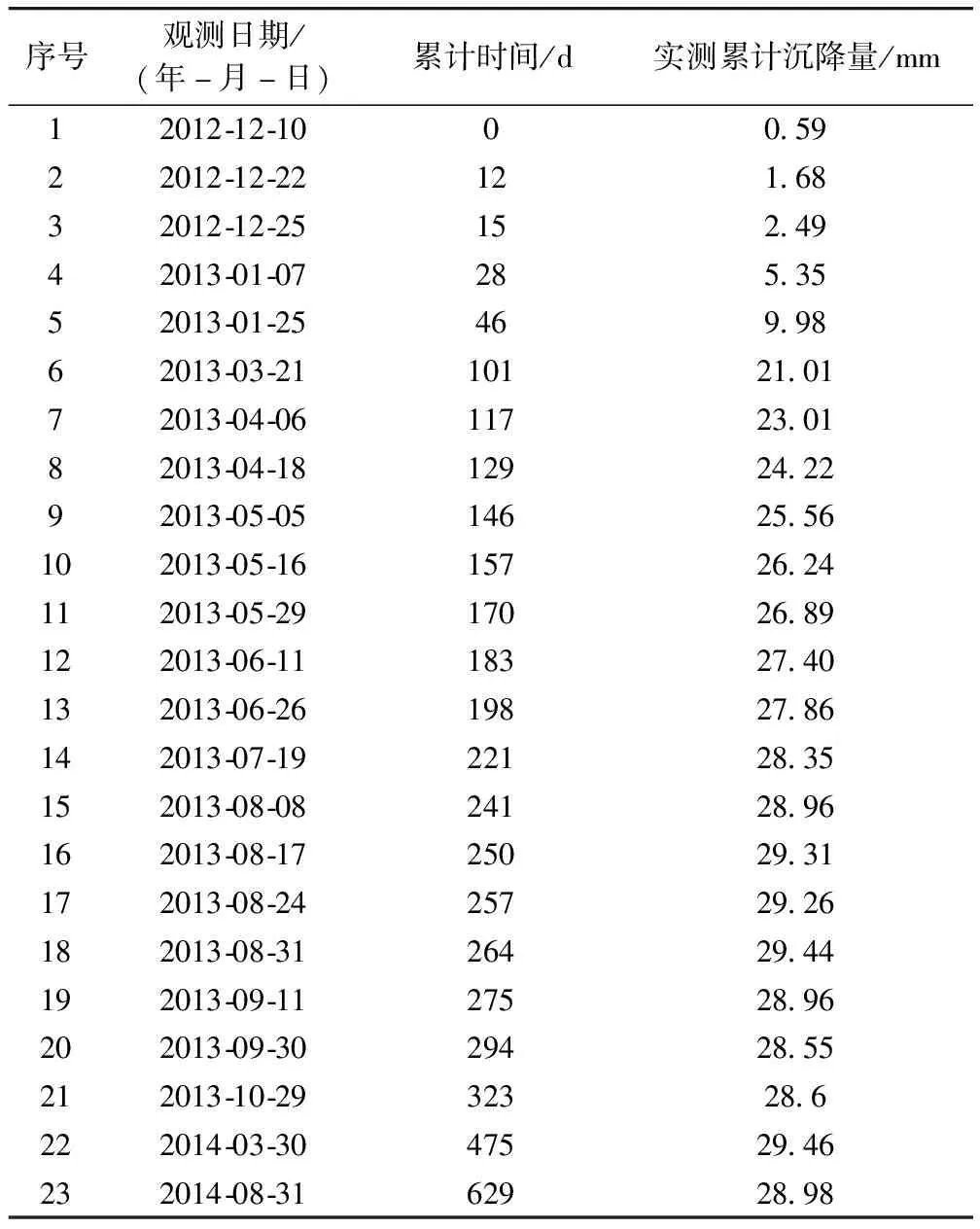
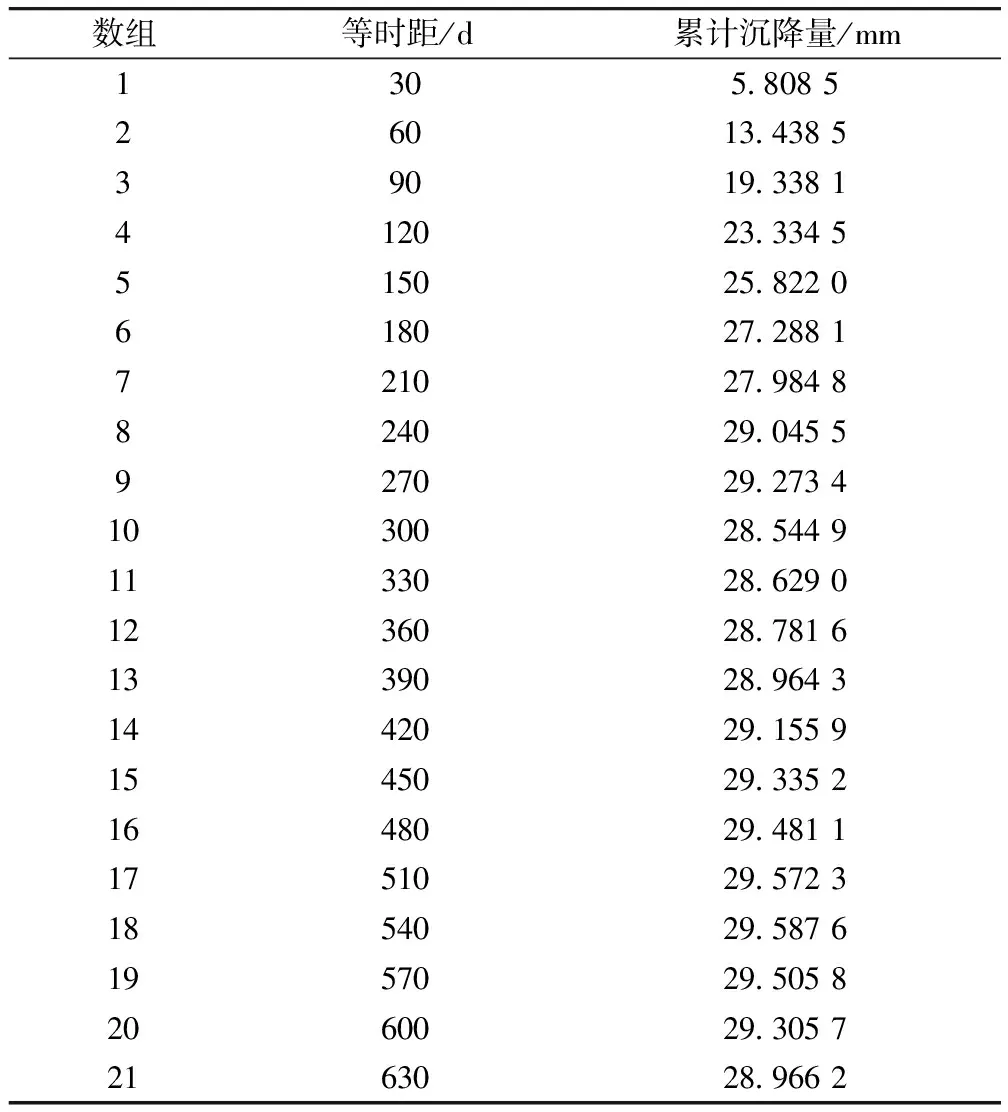
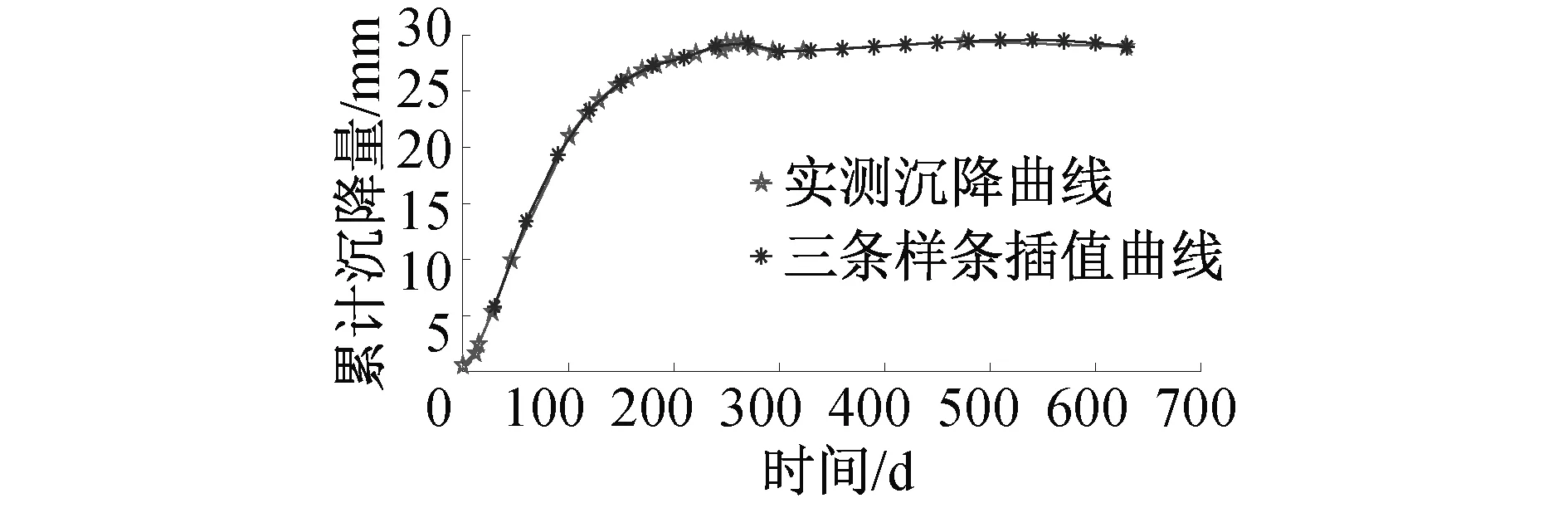
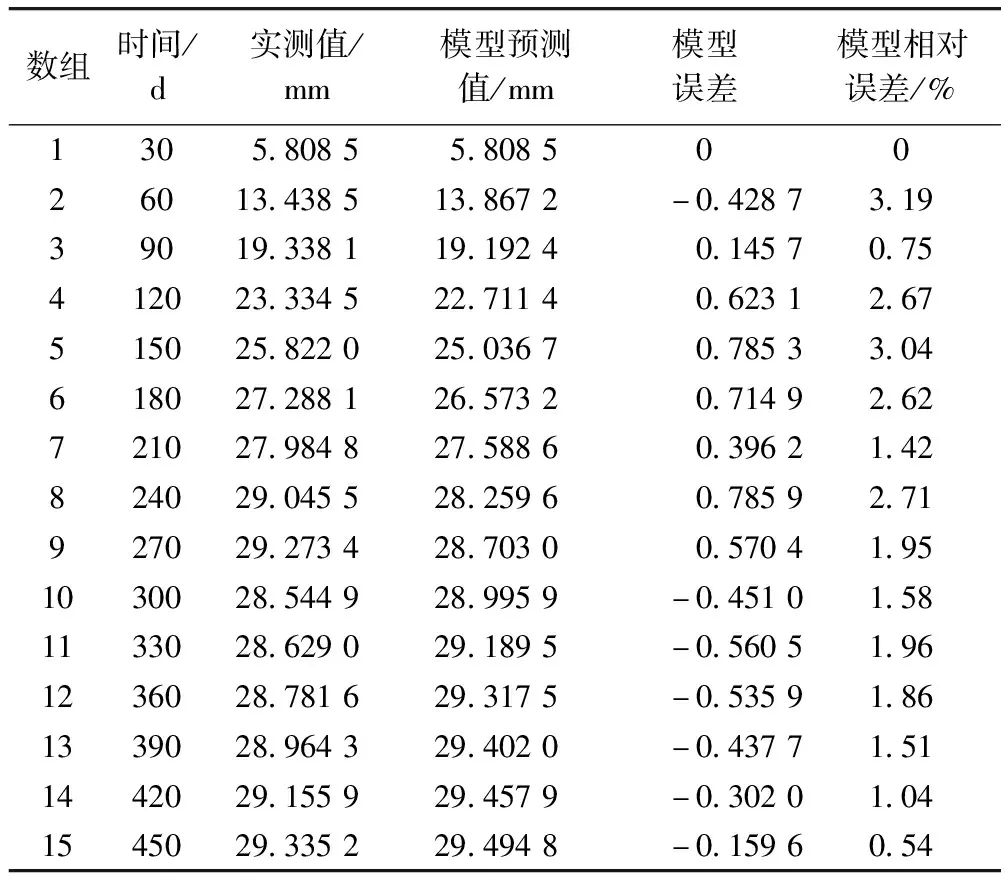
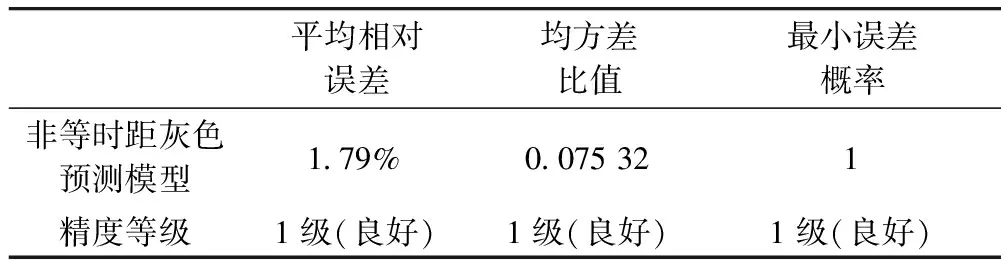
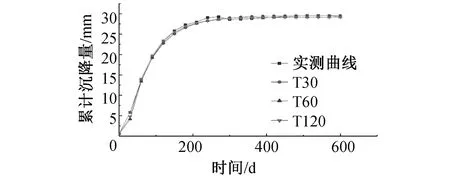
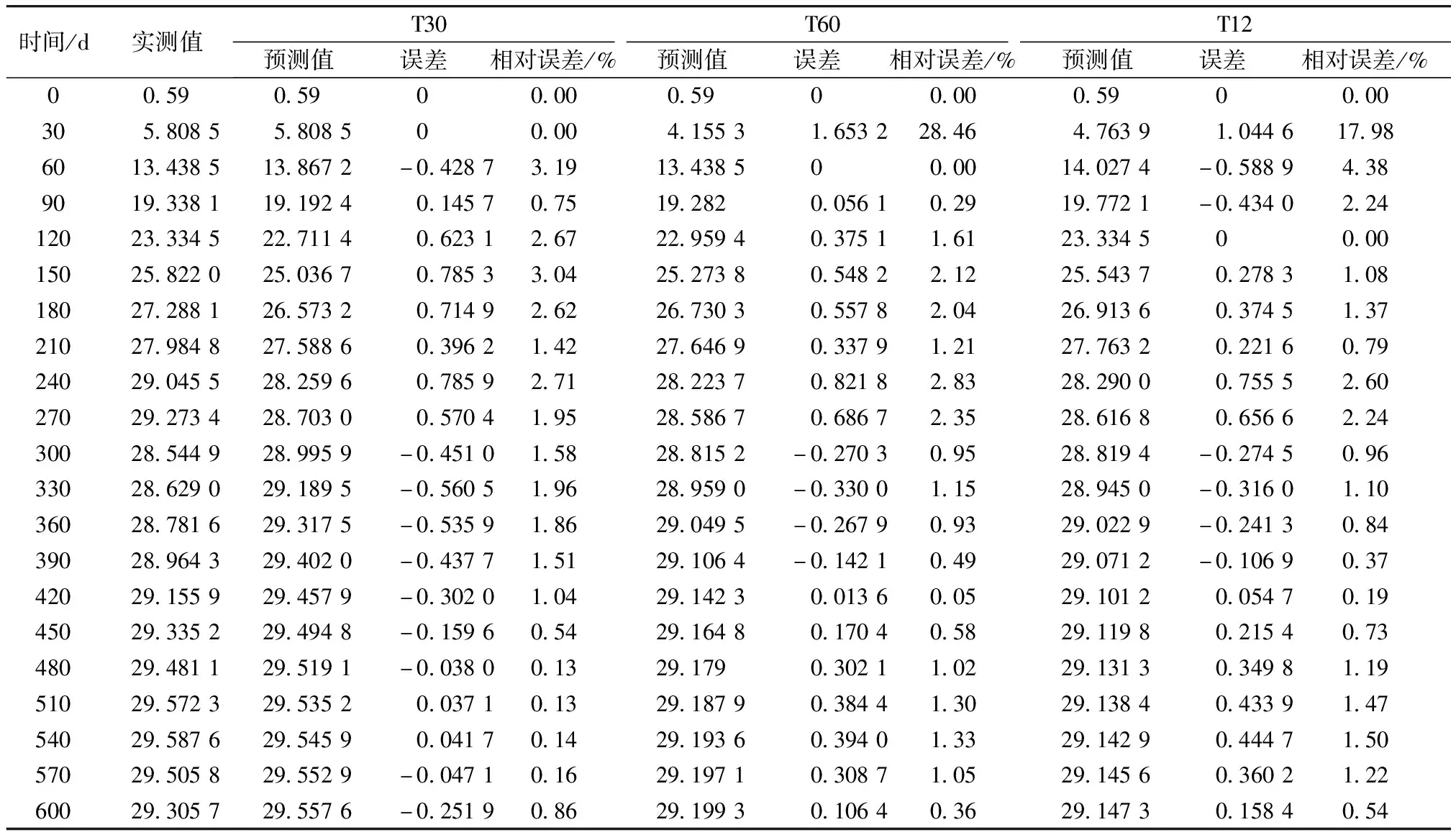
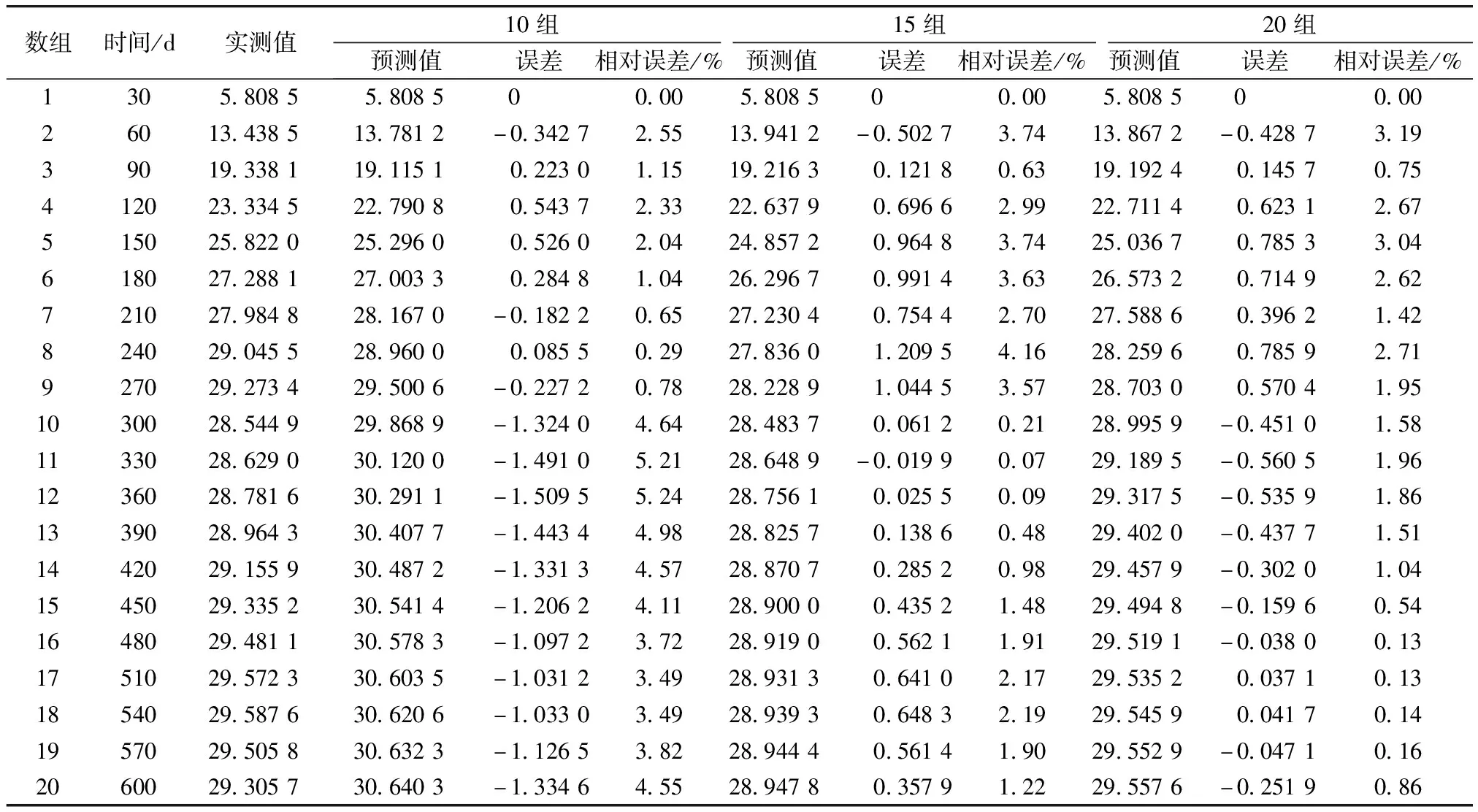
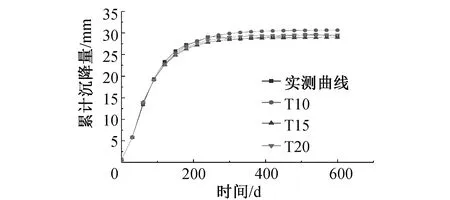
三次樣條插值[10]是依據數學方法,在樣點之間進行插值估算,生成平滑曲線的方法。其數學定義如下:若函數S(x)∈C2[a,b],區間[a,b]之間存在著數據節點a=x0 (1) (2) 對該矩陣進行求解得其結果,代入式(1),可以得到每個小區間的三次樣條插值函數表達式。 考慮到三次樣條插值計算量較大,為此在本文中,利用軟件Matlab工具箱的spline函數[11]完成上述計算。具體代碼如下。 4)插值估算所求時間的對應沉降量:m′=spline(t,p,t′)。 通過上述過程,原始沉降數據就轉化成為了等時距沉降數據,為下一步非等時距灰色預測模型的建立提供應用基礎。 在灰色系統理論中,灰色模型[12-14]建模算法簡單,預測精度高,但觀測時間不是等間隔的。本文所建立的非等時距灰色模型突破了傳統灰色模型應用的障礙,是應用相對簡便而且充分挖掘有價值信息的建模方法,其應用性有巨大潛力。 1)設非等時距灰色預測模型的原始序列為X0: X0={x0(1),x0(2),…,x0(n)} (3) 2)對非等時距灰色預測模型原始數列進行累加,可以得到新的數列X(1): X(1)={x(1)(1),x(1)(2),…,x(1)(n)} (4) 3)X(1)的緊鄰均值生成序列Z(1); Z(1)={z(1)(1),z(1)(2),…,z(1)(n)} (5) 式中:Z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1) (6) 其時間響應式為: (7) 4)采用最小二乘的理論方法計算得到灰度參數值,參數a,b可以通過建立微分方程求解: (8) (9) 5)計算可以求取參數a,b然后代入(7)即可得到非等時距灰色預測模型。 6)將非等時距灰色預測模型計算新生成的數列累減還原,得到模型的擬合值或預測值。 (10) 式中:k為時間序列,k=2,3…n。 以上非等時距灰色模型建立過程。 非等時距灰色模型精度評定具體標準如表1所示。 表1 模型精度評定標準 預測模型的精度大小是由均方差比C和小誤差概率P決定,其計算公式為: (11) (12) (13) 根據以上內容分析,對于本文的非等時距灰色模型算法流程進行簡要總結:首先將建筑物原始沉降數據利用Matlab工具箱完成三次樣條插值,得到基于原始數據的等時距序列,其次進行非等時距灰色預測模型的建立,得到預測沉降數據。然后進行預測值與實測值的沉降量精度對比,計算平均相對誤差、小誤差概率、均方差比值,具體流程如圖1所示。 圖1 沉降預測計算流程 為分析非等時距灰色預測模型應用于建筑物沉降預測的精度效果,根據聊城昌潤祥荷園8號樓J81實測數據,利用Matlab代碼編程進行三次樣條插值法處理,隨后進行非等時距灰色模型的建模,并對預測模型進行精度分析。 昌潤祥荷園8號樓高層住宅樓項目位于聊城市東昌路以北、徒駭河以西新征地塊。共1棟27層高層住宅樓。建筑物主體沉降觀測點使用0.3mm精密水準儀觀測,采用閉合線路二等水準測量。沉降點布置如圖2所示。 圖2 平面沉降點布置 聊城昌潤祥和園8號樓J81實測沉降數據如表2所示。 表2 聊城昌潤祥荷園8號樓J81實測沉降數據資料 根據上文非等時距灰色預測模型理論可知,表2的沉降觀測數據均是非等時距的,而所建立的灰色預測模型是建立在原始數據等時距基礎上的,為此必須進行等時距處理,方便進行下一步建模工作。本次采用三次樣條插值法處理原始沉降數據J81,采用等時間間隔為30d,J81沉降點沉降數據經過三次樣條插值法得到的等時距沉降數據如表3所示。 表3 聊城昌潤祥荷園8號樓J81等時距沉降數據 通過三次樣條插值法得到等時距沉降量,其中1~20屬于內插數值,21屬于外推數值。為保證精度要求,下面對插值效果進行定性定量分析,如圖3所示。 圖3 J81實測曲線與三次樣條插值曲線效果 由圖3可以看出,三次樣條插值法的插值效果是很滿意的,究其原因,在于三次樣條插值法并不是線性插值,區別于線性插值的隆起不平帶來的曲線連續性差,反觀三次樣條插值法在各段連接之處連續性好而且各節點都是光滑連接,因此從根本上保證了插值所得的等間隔序列更加符合工程實際要求,為建立預測模型打下堅實基礎。 X(1)= 計算X(1)的相鄰均值序列,記為Z(1)即: Z(1)= 構造矩陣Y與B: 利用式(8)求灰色參數a=0.414 3,b=12.249 5,則計算得到觀測點的非等時距灰色預測模型的沉降預測公式為: 模型擬合效果比較,比較前15期的擬合精度,如表4所示。 表4 模型擬合效果比較 由表4可知,沉降實測值與預測值誤差范圍為-0.560 5~0.785 9,相對誤差在3%左右。 從檢驗模型的3種方法上看,精度評定等級也很好,滿足了工程要求。其中平均相對誤差越小越好,小誤差概率越小越好,其中均方差比為0.075 32(見表5),數值比較小,說明殘差比較集中,擺動幅度小,原始數據比較分散,擺動幅度大,所以體現的擬合效果是比較好的。 表5 模型擬合精度比較 模型建立的目的是為更好地進行沉降預測,模型預測結果比較如表6所示。 表6 模型預測結果比較 由表6可知,沉降實測值與預測值誤差范圍為-0.594 5~0.041 7,相對誤差在2%左右。 非等時距灰色預測模型的預測沉降值曲線與實測值曲線對比效果如圖4所示。模型預測精度比較如表7所示。 綜上所述,結合圖4以及表5和表7,可以明顯看出擬合結果、預測值與實測值的變化趨勢非常接近,誤差和平均相對誤差都很小,由此可見非等時距灰色預測模型的擬合程度較好,能夠很好地反映出建筑物沉降變化規律。 非等時距灰色預測模型的精度是建筑物沉降預測的核心問題,因此通過對整個建模過程的思考來看,時間間隔、累計沉降觀測數量這兩個關鍵問題的選取顯得至關重要。故本文采用控制變量法,對時間間隔和觀測次數兩種因素進行了預測模型精度分析,為構建高精度的非等時距灰色預測模型提供借鑒。 本文中選取不同時間間隔為T=30,T=60,T=120,控制相同的觀測次數為20,進行預測模型的預測值與實測值精度分析。 通過實測插值沉降量和非等時距灰色建模理論由此可以分別得到T=30,T=60,T=120的非等時距灰色預測模型表達式: (k=2,3,…,n) (14) (k=2,3,…,n) (15) (k=2,3,…,n) (16) 由非等時距灰色預測模型表達式可計算各時段的沉降預測值,得到各觀測點的沉降預測曲線,從而與實際沉降觀測數據進行比較,如表8所示。 進一步計算T30,T60,T120的平均相對誤差分別為:1.35%,2.39%,2.04%。 為進一步觀察出預測模型的精度,繪制實測曲線與相同觀測次數下不同等間隔T30,T60,T120的曲線對比效果如圖5所示。 通過表8與圖5,可以很明顯看出等時間間隔為30d的預測模型精度更優,更加貼近實測曲線,結果表明不同時間間隔,控制不同的沉降觀測次數所建立的模型,表明短時間間隔的預測模型精度更好。 圖5 實測曲線與相同觀測次數下不同等間隔的曲線對比效果 表8 不同等時間間隔下相同觀測次數的誤差統計 其次控制相同的時間間隔為T30,不同的觀測次數。選用10組、15組以及20組建立預測模型進行精度分析,如表9所示。 表9 不同觀測次數下相同等時間間隔的誤差統計 通過計算可以得到10組、15組以及20組所建預測模型的平均相對誤差分別為:2.93%,2.92%,1.32%。 為更清晰觀察其預測效果,繪制實測曲線與相同時間間隔T30下不同觀測次數10組、15組、20組的曲線對比效果,如圖6所示。 圖6 實測曲線與相同時間間隔T30下不同觀測次數曲線對比效果 通過對比,可以發現20組所建立的灰色預測模型預測精度是更優的。結果表明:相同的時間間隔,不同的沉降觀測次數所建預測模型,長時間觀測次數的預測模型精度更優。 1)通過本文所建立的非等時距灰色模型,對建筑物沉降進行預測,其擬合效果是滿足要求的,精度水平也達到了一級,從而驗證了本文非等時距灰色模型在建筑物沉降預測中的可行性,也為其他類似工程預測提供了參考。 2)三次樣條插值法處理建筑物實測數據,尤其是在非等時距序列方面體現出優越的擬合效果,其主要因為是良好收斂性、穩定性優越以及二階光滑度即二階導數連續等特點,可以在工程數據處理中起到重要作用,為其他類似工程數據處理提供借鑒。 3)本文所建立的非等時距灰色預測模型設置了兩個控制因素(時間間隔和觀測數據量),當這兩個控制因素取值不同時,模型預測結果的精度也不同。選擇短時間間隔且長時間觀測次數的預測模型精度上會得到更好的預測效果,增加了預測模型的可調節性和優化可能性。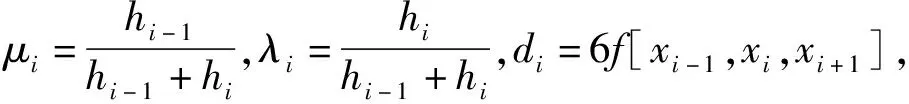
1.2 非等時距灰色模型的建立
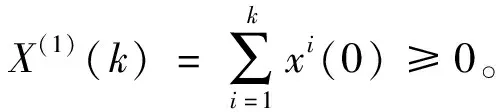
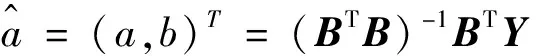
1.3 非等時距灰色模型的精度檢驗
1.4 非等時距灰色模型的算法流程
2 工程應用實例
2.1 項目概況
2.2 沉降監測數據處理
2.3 非等時距灰色模型建立
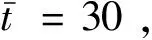
2.4 非等時距灰色模型精度分析

3 影響非等時距灰色模型精度的關鍵問題
3.1 不同等時間間隔下相同觀測次數的精度分析
3.2 不同觀測次數下相同等時間間隔的精度分析
4 結語

