三相交錯LLC諧振變換器空載問題的研究

劉宏洋，張萌，何清林

（黑龍江科技大學電氣與控制工程學院，黑龍江哈爾濱，150022）

0 引言

LLC諧振變換器拓撲結構簡單，且可在原邊實現ZVS以及副邊實現ZCS，所以其應用已進行了長足的發展，相較于過去的幾十年，應用領域已越來越廣泛，以至于對LLC諧振變換器的性能、效率、功率密度、EMC、EMI等提出了更高要求。對于單相LLC諧振變換器來說，在輸出端只設置電容作為濾波元件，并無電感，變壓器二次繞組注入的整流正弦波電流在輸出濾波電容上產生了較大的電壓紋波，諧振頻率又是開關頻率的二倍，這就導致了濾波電容量需要很大，就會不利于功率的等級提升。而三相交錯LLC諧振變換器除LLC變換器的眾多優點之外，還由于三橋臂互差120°，此拓撲易于均流，利用相位差，使電流相互交疊，消除一部分紋波，導通電流有所降低。

LLC諧振變換器工作在不同環境中時，隨著負載工況的改變及輸入側電壓的差異，原邊會失去軟開關特性，變為容性開關，使工作的可靠性降低，尤其是在輕載工況時，開關頻率高就會使開關損耗急劇上升，致使輸出側電壓不受控制，變換器效率降低，而在傳統的設計中一般會選擇增加假負載，但無形中增加了一部分額外的損耗，因此解決以上問題和輕載時增益失真問題就十分重要。

1 設計方案

1.1 三相交錯LLC諧振變換器結構

三相LLC諧振變換器采用星型聯結，可實現各相均衡電流，每一相都有開關、諧振腔、變壓器、整流濾波單元以及負載構成。開關網絡是由三相半橋逆變的六個功率開關管組成，每一個功率開關管都會并聯一個體二極管，正是由于體二極管的存在才實現了軟開關；諧振網絡包括諧振電感Lr、諧振電容Cr和勵磁電感Lm；變壓器和整流網絡進行能量的傳輸；濾波網絡對輸出端產生的電流紋波進行吸收，以延長變換器的運行壽命；而負載就代表著變換器的運行工況，負載的不同就需要不同的控制策略，以避免在輕載狀態時電壓失控現象的發生，所以使變換器在不同工況下都能穩定運行是非常重要的。

1.2 空載優化問題的研究

圖1 電路原理圖

LLC諧振變換器中存在寄生元器件，在重載運行時，這些寄生元器件對電路有極小的影響，甚至沒有影響，但是隨著所加負載的逐漸減輕，寄生元器件的影響就開始顯現，甚至可以影響電路的正常運行。在三相LLC諧振變換器中變壓器的匝間電容和副邊整流二極管結電容就是主要的影響因素，將其統稱為寄生電容，其表達公式為：

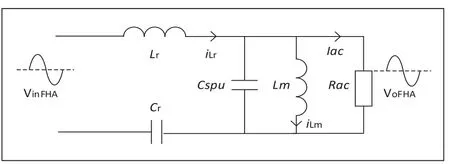
圖2 FHA下的電路等效模型

在整流網絡中器件都為純阻性，因此電壓與電流不存在相位差，則整流網絡輸出端的電流（IO）與輸入側電流的有效值（Ir）之間的關系為：

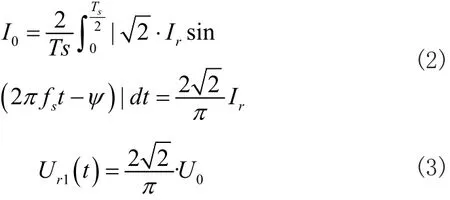
中心抽頭式變壓器原邊副邊匝數比為n:1:1，將輸出側阻抗換算到原邊，對輸出側阻抗進行歸一化處理，得：

得輕載工況下傳遞函數：

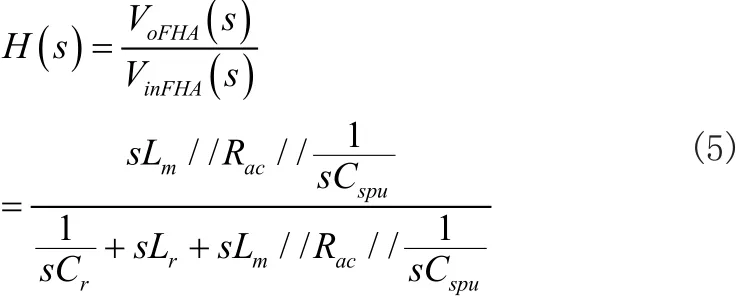
則輕載工況下增益為：

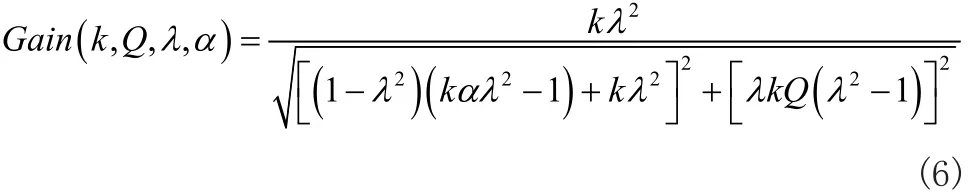
由圖3可見，隨著負載工況的減輕，寄生電容的影響會變得愈來愈明顯，在諧振網絡中會多出一個高頻率的諧振點，而考慮到寄生電容因素影響曲線示意圖才會與現實工況相接近。在實際工況中，隨著負載的逐漸降低，輸出側電壓就會不斷升高，工作頻率就會隨之增大，由于寄生電容的存在，達到某一工作頻率范圍時，增益曲線就會重新多出一個拐點頻率，導致輸出端電壓不穩定，增益就會失真。為優化寄生電容在輕載工況中的影響，就需要合理的設計Q值和k值。

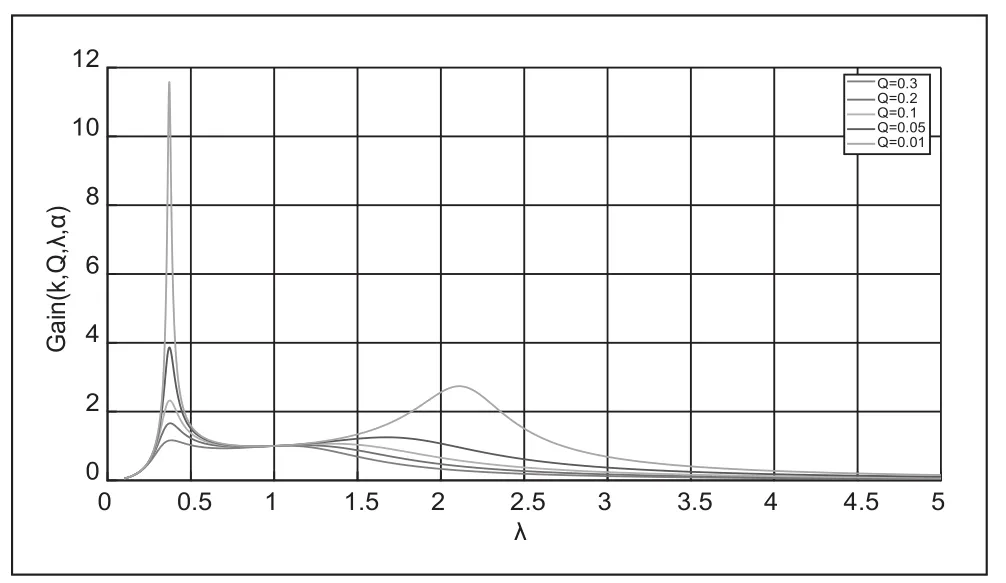
圖3 考慮寄生電容影響下的直流增益曲線圖

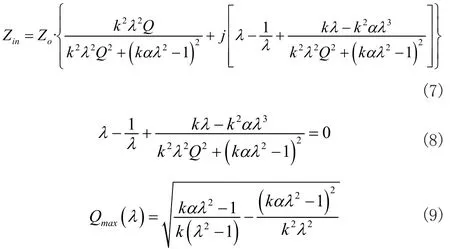
當阻抗角極小時，諧振網絡會工作在感性區域與容性區域之間的臨界區域，此時的變換器會存在一定的運行風險，所以Q值要相對小于Qmax，使變換器穩定工作，以實現原邊的ZVS。隨著Q值得減小，增益電流就會愈來愈大，負載變小得情況下所受寄生電容干擾就會愈來愈強，增益曲線的性能就會變差。

如圖1-4所示，當k值不同時，相應的直流增益曲線也不盡相同，工作頻率也不盡一樣。當k值愈來愈大時，直流增益卻愈來愈小，所得到的工作頻率的范圍就愈來愈大，那也就是說所有的變量中只有k值發生變化時，相同負載工況下，Lr和Cr是一定的，k值變大，那么隨之變大的就是Lm，那么勵磁電流就會降低，以至于開關損耗也會隨之變小。

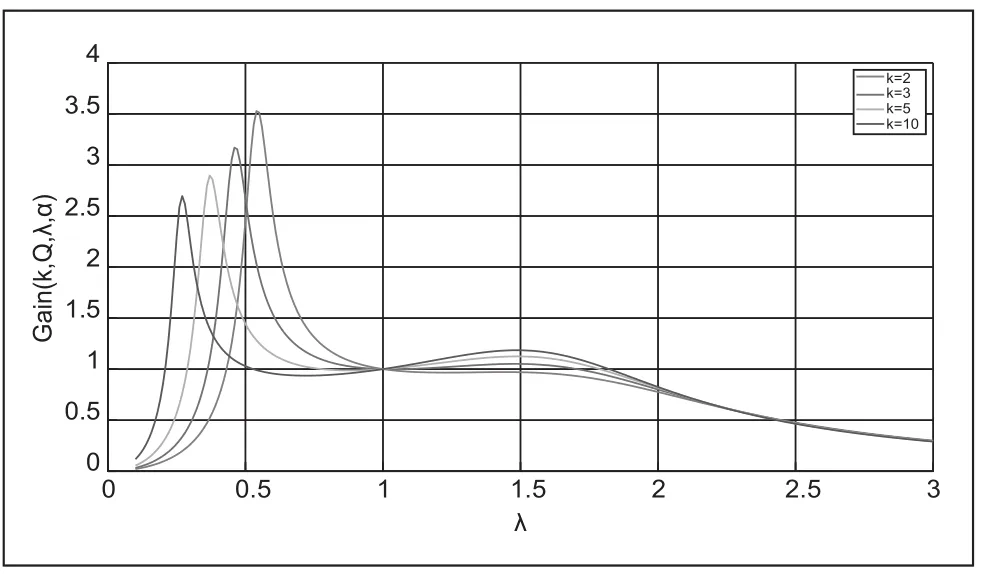
圖4 不同k值下直流增益曲線圖

2 實驗結果

輸入側電壓給定為400V，Q值給定為0.323，k值給定為 6，Lm、Lr、Cr的給定分別為：10.224uH、1.276uH、483.76nF，工作頻率范圍設定為100kHz～200kHz，通過調節變換器的帶載能力，分別測得重載工況與輕載工況下的輸出側電壓波形、驅動脈沖信號波形以及變換器一次側電壓輸出波形，波形如圖5、圖6所示，可以清晰的看出，在輕載工況下，其驅動脈沖信號波形和變換器一次側電壓輸出波形仍存在失真，這正是因為有寄生電容的存在，才導致該現象的產生，所以要繼續優化Q值、k值，以削弱寄生電容的影響。

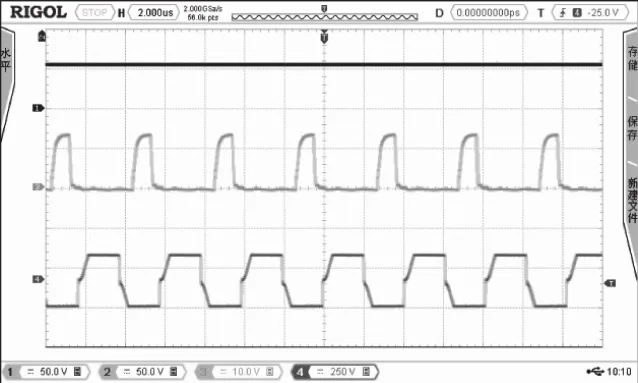
圖6 輕載工況下波形圖

3 結論

在此處分析了變壓器匝間電容與整流管結電容對三相LLC諧振變換器輕載工況時的影響，在輕載工況下如果不考慮寄生電容，所生成的直流增益曲線與實際情況有很大的出入，導致變換器不能在全工況下穩定運行，甚至會損壞變換器。通過分析優化變換器輕載啟動的因素，以確定出最優的Q值與k值，將損耗與危害降到最低，最后通過實驗來證明理論與策略的正確性與可靠性。