融入數形結合思想 有效建構數學概念

☉羅二連

在小學生學習數學概念時，要能夠融進數形結合的思想來賦予數學概念具象化的特征，從而讓學生能夠從直觀中提取出對概念的理解，進而能夠建立概念性數學認知。那么，如何在“倍數與因數”一課的教學中利用數形結合思想來促進學生深入理解數學概念呢？

一、在數形結合中引入數學概念

在數學概念教學時，引入數學概念是極為重要的環節。在這一環節之中借助于數形結合可以讓學生直觀形象地感知數學概念產生的生活基點，有效地實現數學學習的生活化。

例如，教學“倍數和因數”一課，我就是利用數形結合的方式引出數學概念，促進學生直觀地感知數學概念。

教學片斷：用課件呈現“用12個邊長1 厘米的小正方形拼擺成一個大長方形，有多少種擺法呢？”

師：請大家拿出自己手中的小正方形，拼一拼、擺一擺。

學生嘗試擺成長方形，教師巡視指導。

師：誰來說一說自己的擺法。

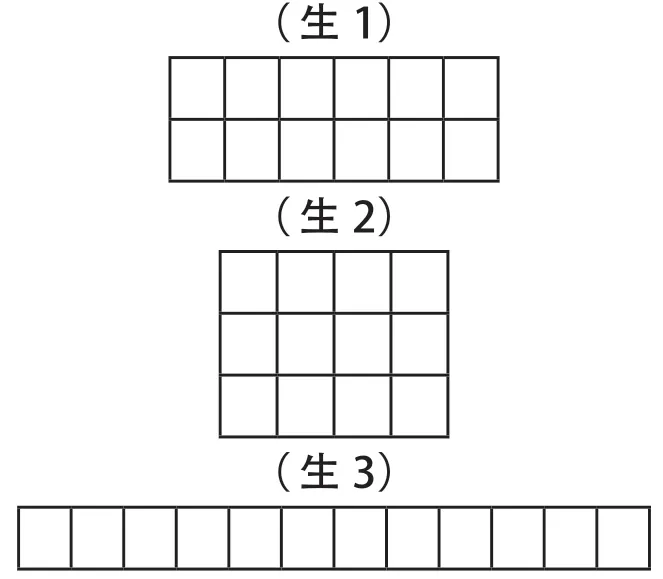
生1：我是這樣拼擺的，將這12 個小正方形擺成2 行，每行6 個。

生2：我擺成的長方形，長是4 厘米，寬是3 厘米。

生3：我是這樣拼擺的，擺成1 行，12 個連著在一排。

在學生匯報后，教師用課件依次地給學生呈現拼擺的三種不同方法。

師：你們能用乘法算式來表示它們的面積嗎？

指名學生說說。

教師依據學生的回答，依次板書：1×12=12，2×6=12，3×4=12

師：同學們，我們今天學習的內容就是倍數和因數。比如，在2×6=12 這個算式里，誰是誰的倍數？誰又是誰的因數呢？

生4：我想12 應該是2 的倍數，12 是6 的倍數，因為12 這個數大。在平時的學習中，我們有時候會遇到“12是2的幾倍？”這樣的問題。我就是這樣理解的。

師：你想得真好呀！能夠根據經驗來思考數學問題。

師：再請同學們猜一猜另外兩道算式里的數，看一看誰是誰的倍數、誰又是誰的因數。

生5：12 是3 和4 的倍數，3和4 是12 的因數。

生6：1 和12 是12 的因數，12 是1 和12 的倍數。

師：這兩個“12”是一樣的嗎？

生7：不一樣，一個是乘數，另一個是積，表示的是兩個數。

在上面的教學活動中，教師能夠通過讓學生動手拼擺小正方形的方式，利用好數形結合，促進學生初步感受數與數之間的“因數和倍數”關系。不僅引入了倍數與因數的概念，也為下面將要進一步探究“因數和倍數的研究范圍不包括0，且是整數”這樣的知識做了鋪墊。

二、在數形結合中抽象出數學概念

在數學概念的理解活動中，引領學生抽象出數學概念是極為重要的。唯有做到抽象概念，才能使學生深刻地理解概念。滲透數形結合思想可以有效地讓學生經歷抽象數學概念的全過程，進而能夠達到更佳的教學效果［1］。

例如，在教學“倍數和因數”時，我是這樣引領學生抽象出概念的。

師：請同學們觀察這些算式“1×12=12，2×6=12，3×4=12”，看看它們都有怎樣的特點？

生1：都是乘法算式，積都是12。

生2：乘數和積都是整數。

師：從圖上來觀察的話，它們可以是0 嗎？為什么？

生3：不可以是“0”，因為拼擺成長方形的長與寬都是整數，不可能是“0”。

師：對的，研究因數和倍數的范圍是非“0”的自然數。

師：能用更好的辦法來表示出數與數之間的倍數與因數關系嗎？

生4：可以用字母來表示呀。

師：如果用a 和b 來表示兩個乘數，用c 來表示積的話，怎么來表示出它們的關系呢？

生5：如果a×b=c（均是不為“0”的自然數），那么，我們就說a 和b 是c 的因數，或者說c 是a 和b 的倍數。

……

在上面的教學活動中，教師能夠緊緊圍繞數形結合進行概念的抽象，既依靠圖形來引領學生深入理解倍數與因數的概念，同時也是引領學生從直觀中走向抽象化數學學習的最有效途徑。

三、在數形結合中內化數學概念

借助于數形結合思想可以更好地促進學生將數學概念進行內化理解。在數學教學之中，學生一旦對數學概念有了初步的感知與理解，教師就要及時地促進學生在數形結合中內化數學概念。

師：上面的2×6=12 算式可以改寫成除法算式嗎？

生：能。

師：可以改寫成什么呢？

生：12÷2=6，12÷6=2。

師：如果用字母來表示的話就是什么呢？

生：c÷a=b 或者是c÷b=a。

師：a、b、c 不管什么數都可以嗎？

生1：不是的，除數不能為“0”，這里的a和b都不能是“0”。

師：a 和b 都不能是“0”，那么，c 有可能是“0”嗎？

生：那就都不可能是“0”了。

師：從圖上可以看出來嗎？

生：也可以看出來，拼成的長方形的面積、長與寬都不可能是“0”。

師：我們以前學習過“幾倍”的“倍”與“倍數”的概念相同嗎？有什么差異呢？請同學們交流一下。

……

通過學生的熱烈討論，最終得出了：“幾倍”與“倍數”其實都是指兩個數之間的倍比關系；不同的是它們的研究范圍不同，“幾倍”涉及到可以是不是0的所有數，可以是小數、分數、整數，而“倍數”的研究范圍只是非0 的自然數。

因而，僅僅靠范例來引領學生加強對概念的理解是不夠的，還要能夠將其與相近的概念進行比較與辨析，這樣才能讓學生對概念的理解更加清晰，不再會混淆。

四、數學結合中建構數學概念

引領學生能夠在數學概念的學習中建立模型也是數學學習的重要目標。因而在具體的學習過程中也要能夠借助于數形結合來有效地促進學生對所學數學概念建立模型，進而努力實現教學效益的最大化［2］。

師：我們可以用擺小正方形拼成長方形的辦法來理解因數與倍數的概念，同樣也可以用擺小正方形的辦法來尋找一個數的倍數。比如說，找出5 的倍數有哪些？可以怎么做呢？

生1：可以先擺1 行，每行有5 個，一共也就是5 個；再擺2行，每行有5 個，一共就是10 個正方形。以此辦法進行下去，就可以找出5 的倍數有：5、10、15、20、25……

生2：那么列算式的話，也就是5×1=5；5×2=10；5×3=15……

教師利用課件給學生呈現用拼擺的方法找出5 的倍數的操作畫面，讓學生從直觀上感知5 的倍數有5、10、15、20……

師：同學們，你們能用畫圖的方法來找4 的倍數有哪些嗎？

學生自己在本子上畫一畫，并列出算式。

師：4 的倍數有哪些呢？說說你的想法。

學生匯報，教師依據學生的回答進行板書：4×1=4，4×2=8，4×3=12……

師：如果是a 呢？

生1：a×1，a×2，a×3，a×4……

師：用怎樣的方法來求一個數的倍數？

生：用一個數乘上非0 自然數的方法來求出它的倍數。

師：一個數的倍數的個數有多少呢？

生：有無數個。因為非0 的自然數也有無數個。

師：從我們列舉的幾個例子可以看出一個數的倍數的特征嗎？請同學們認真交流一下。

生3：一個數的最小倍數是它的本身。

生4：一個數沒有最大的倍數。

師：對的，一個數的倍數的個數是無限的，其中最小的倍數是它的本身，沒有最大的倍數。

……

由此，學生經歷了探求一個數的倍數的方法，以及觀察發現了一個數的倍數的特征。在教師的有效引領中，學生經歷了數學感知、發現與應用的全過程，可以說很好地實現了數學學習中的“教學做合一”。

總而言之，在小學數學概念的理解與應用教學活動中，教師要能夠積極借助數形結合思想引發學生對于概念的學習，幫助學生能夠自主地對數學概念進行深入理解，逐漸建立認知結構。