基于階梯形標定物的線激光傳感器手眼標定算法

孫煒，舒帥，李汶霖，劉乃銘，苑河南，劉權利

（1.湖南大學電氣與信息工程學院，湖南長沙 410082；2.大連理工大學大連理工大學-立命館大學國際信息與軟件學院，遼寧大連 116000；3.湖南大學汽車車身先進設計制造國家重點實驗室，湖南長沙 410082）

隨著工業自動化的普及，生產制造領域對工業機器人的需求與日俱增，機器人視覺系統是工業機器人的重要組成部分.在機器人視覺系統中，視覺傳感器有兩種安裝方式：非固定視點方式（eye-inhand）和固定視點方式（eye-to-hand）.非固定視點方式是將視覺傳感器固定在機器人的末端執行器上，機器人運動可帶動視覺傳感器多視角掃描被測對象；固定視點方式是將視覺傳感器與機器人分離，這種安裝方式通常會產生視覺死角.本文采用非固定式的安裝方法.在機器人的加工生產中，需要通過視覺傳感器獲取工件的準確位置，以便進行焊接、抓取、涂膠等作業，這時就需要求解視覺傳感器坐標系相對于機器人基坐標系的齊次變換關系，上述過程稱之為機器人的手眼標定.機器人的手眼標定精度最終會影響整個系統的加工作業精度.

Tsai 和Lenz［1］提出了基于視覺傳感器的標定板多視角成像方法，并根據約束關系建立AX=XB方程求解手眼關系矩陣，但該方法標定精度較低，魯棒性弱；Horaud 等人［2］提出了一種簡化版的手眼標定算法，該算法主要優點在未知數個數不變的前提下，同時解得手眼關系的旋轉矩陣和平移向量，但該方法計算復雜度高，易受離群點影響.Liu［3］等人提出了一種精度高、魯棒性強的手眼標定方法，該方法利用離群點檢測解決了數據預處理的問題，顯著提高了手眼標定精度，但該方法迭代次數高，計算工作量大；Xie［4］等人提出了一種基于標準球面的手眼標定方法，融合離群點檢測和微分計算提高了手眼標定精度，但該方法操作復雜，實驗數據龐大；蔡曉潔［5］等人用RASANC 算法剔除原始數據中的離群點，取得了更穩定的匹配結果，但其算法計算復雜度高；蘭浩［6］等人提出了一種基于球形標定物的線掃描相機手眼標定方法，但該方法操作復雜且極易出錯；王英男［7］等人提出了一種適用于線激光器的手眼標定方法，但該方法需要多姿態掃描固定點，計算工作量大；牛延平［8］深入研究了球形標靶擬合及中心定位算法，但該算法的精度易受實驗環境和設備的影響；Yang［9］等人提出了一種基于半球面的手眼標定方法，但該方法需要根據視覺傳感器設定的坐標系對標定點的y值進行判斷，標定容易失敗；Hu［10］等人提出了利用單線激光模塊輔助攝像機標定的算法，但該算法要求采集到的激光輪廓數據與機器人的姿態數據必須成非線性關系；Zeng［11］等人提出了一種分步式手眼標定算法，該算法首先通過最小二乘法解得旋轉矩陣，再由旋轉矩陣求得平移向量，但該方法過程繁瑣且計算復雜；Liska 等人［12］提出了一種二維激光輪廓掃描相機的手眼標定方法，該方法利用迭代算法分步求解手眼關系矩陣，但未剔除離群點且迭代周期長.

1 線激光傳感器手眼標定

1.1 球形標定法原理

目前，在線激光傳感器的手眼標定算法中，基于球形標定物的標定算法應用最為廣泛.該方法通過線激光傳感器掃描球形標定物，以標準球的球心作為標定點，控制機器人帶動線激光傳感器多位姿掃描標準球，再根據球形標定物的幾何特性［6］和勾股定理求取標準球球心在線激光傳感器坐標系下的坐標，計算流程如下：

設標準球的球心P在機器人基坐標下的坐標為Pb(xb，yb，zb)，在線激光傳感器坐標系下的坐標為Ps(xs，ys，zs)，Ps可通過式（1）轉換到Pb.

設線激光在標準球上投射形成的激光圓的圓心在線激光傳感器坐標系下的坐標為O(x0，y0，z0)，標準球球心在線激光傳感器坐標系下的坐標為Ps(xs，ys，zs)，坐標O與坐標Ps的幾何關系如圖1 所示.

圖1 截面圓圓心與球心的幾何關系Fig.1 The geometric relationship between the center of the cross-sectional circle and the center of the sphere

由圖1 可知，激光圓的圓心坐標與標準球的球心坐標存在式（2）的關系：

式中：R為標準球體的半徑，r為激光圓的半徑，ys的正負需要根據線激光傳感器設定的坐標系方向來判斷.

線激光傳感器多次掃描后可構成點集Psi=(Ps1，Ps2，…，Psn)，Pbi=(Pb1，Pb2，…，Pbn)，i=1，2，3，…，n，n為線激光傳感器掃描的次數.以掃描4 次為例，將獲得的Pbi和Psi代入式（1）中，再運用最小二乘法求解，便解得手眼標定的齊次變換矩陣.

在實際標定過程中，基于球形標定物的手眼標定算法主要存在以下問題：首先，觸碰標準球可能會導致標準球的位置發生改變，進而導致標準球的球心在機器人基坐標系下的坐標發生變化；其次，某些末端執行器（例如抓手）無法通過直接觸碰標準球表面的方式進行手眼標定，獲取標準球的球心坐標變得更加困難；同時，基于球形標定物的手眼標定算法至少需要機器人4 次以不同的姿態掃描標準球，且對于每次激光輪廓傳感器采集的數據，都需要進行圓分割和擬合，計算復雜度高，標定過程復雜；同時，在獲取標準球球心在線激光傳感器坐標系下的坐標值過程中，需要根據激光傳感器設定的坐標系方向判斷y值的正負，該過程容易出錯，且出錯后將導致標定失敗；此外易受到噪聲等因素的影響，球形標定法的標定結果魯棒性較差，上述因素容易造成標定精度不理想，標定結果不穩定.

1.2 改進方法

為解決基于球形標定物的線激光傳感器標定算法精度低且標定過程繁瑣的問題，本文設計了一種階梯形標定物，并基于階梯形標定物提出了一種線激光傳感器標定算法

1.2.1 標定物設計

針對基于球形標定物的線激光傳感器標定過程繁瑣的問題，本文設計了一種階梯型標定物，階梯形標定物的實物圖如圖2所示.

圖2 階梯形標定物實物圖Fig.2 Physical map of step-shaped calibrators

該階梯形標定物由正方體合金塊切得，其加工精度為a，長、寬、高分別為l、w、h，每層階梯的高度為b，且每級階梯上有兩個標記點.

階梯型標定物的三視圖如圖3 所示，圖3（a）、圖3（b）、圖3（c）分別為該標定物的正視圖、俯視圖、左視圖.俯視圖中每個階梯上有兩個標記點，標記點將每層階梯的長度三等分，也可以被稱為三等分點.

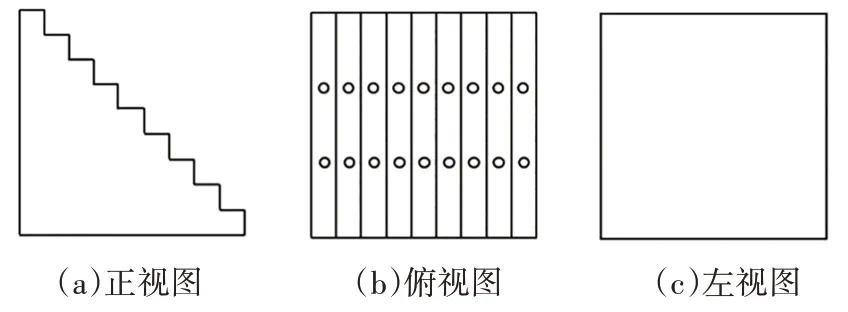
圖3 階梯形標定物三視圖Fig.3 Three views of step-shaped calibrators

1.2.2 基于階梯形標定物改進的標定算法

本文提出的標定算法分為如下幾步：1）獲取標定點在線激光傳感器坐標系下的坐標Ps；2）獲取標定點在機器人基坐標系下的坐標Pb；3）利用Pb和Ps建立約束方程，通過最小二乘法求解手眼關系矩陣.本文提出的標定算法流程如圖4所示.

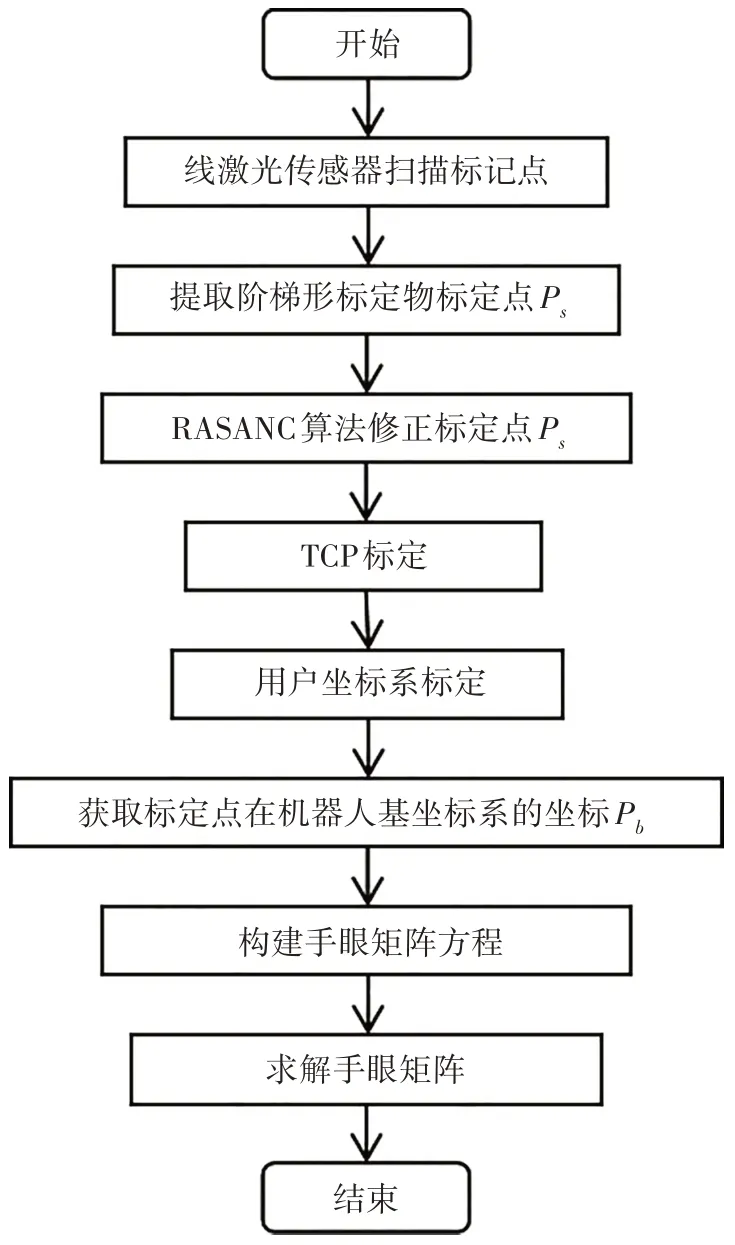
圖4 標定算法流程圖Fig.4 Flow chart of calibration algorithm

1）獲取標定點在線激光傳感器坐標系下的坐標Ps

本文選取階梯形標定物的角點作為標定點，這些角點構成實驗標定點集；為獲得標定點在線激光傳感器坐標系下的坐標Ps，需要機器人帶動線激光傳感器運動，并使線激光對齊階梯型標定物上同側的每一個標記點，如圖5 所示；再利用線激光傳感器掃描階梯形標定物并獲取階梯的輪廓數據，提取階梯輪廓數據的每個標定點Psi(xsi，0，zsi)，i=1，2，3，…，n，n為標定點的總數；本文使用前輪廓的角點作為標定點集Pnew，如圖6所示.

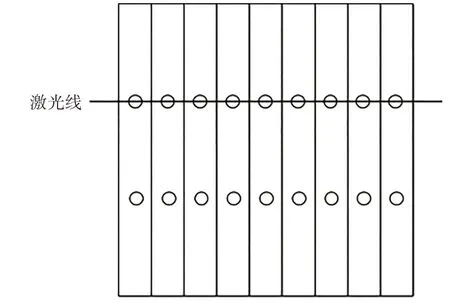
圖5 線激光掃描示意圖Fig.5 Schematic diagram of line laser scanning

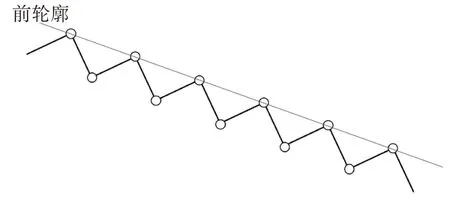
圖6 階梯形標定物的輪廓角點Fig.6 Contour corner points of step-shaped calibrators

由于球形標定法需要對球心坐標的y值進行修正，若未修正，則會導致手眼標定精度較低.為解決這一問題，本文將線激光傳感器的掃描平面設置為XOZ平面，則標定點在線激光傳感器坐標系下的坐標可表示為(xs，0，zs)，通過這種方法可以不需要對標定點的y值進行修正.

獲取標定點集Pnew的具體計算方法如下：

（a）設階梯輪廓數據共有k個標定點，設第i個標定點在線激光傳感器坐標系下的坐標為(xi，0，zi)，i=1，2，3，…，k，k為輪廓數據中標定點的總數；對每一個點(xi，0，zi)做式（3）的運算，求取di，式（3）中sinθ，cosθ計算方式分別如式（4）、式（5）所示：

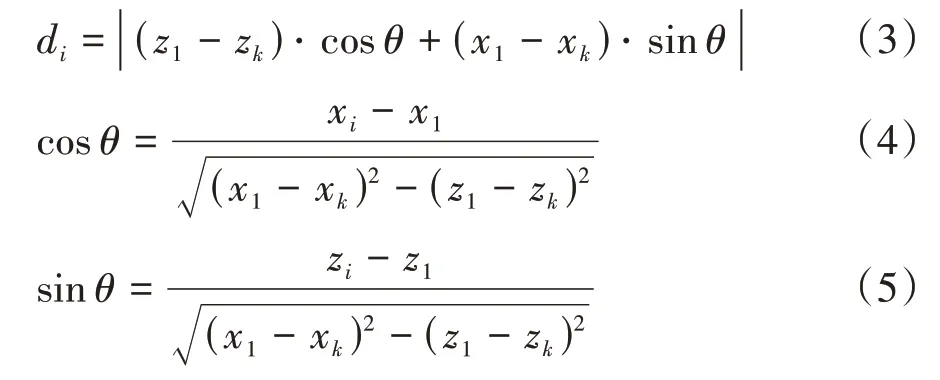
（b）取di值最大時對應的點，若大于設定的閾值，則判斷該點為角點，并保存該點，設該點的索引為l，則以點(xl，0，zl)為分界，將該輪廓分割為前后兩個子集合，繼續遞歸搜索前輪廓的角點直至檢測到所有角點，這些角點構成標定點集Pnew；否則，判定該輪廓為直線，不存在角點，結束標定點搜索.

（c）在獲得階梯形標定物輪廓的標定點集后，利用RASANC 算法［13］對標定點集Pnew進行直線擬合，擬合得到的直線方程為ax+bz+c=0，并根據直線方程修正離群的標定點.具體方法如下：計算標定點集Pnew中每個點到擬合直線的距離df，若df大于用戶設置的閾值Δs，則認為該點為離群點，將該點的x坐標代入擬合直線中，對該點進行修正，用修正后的點替代離群點；否則，不存在離群點，無需對特征點進行修正.

經過上述流程，可以得到標定點在線激光傳感器坐標系下的坐標Psi(xi，0，zi)，i=1，2，3，…，n，n為Pnew中標定點的總數.

2）獲取標定點在機器人基坐標系下的坐標Pb

圖7 用戶坐標系標定示意圖Fig.7 Schematic diagram of user coordinate system calibration

由圖7 可知，本文以點o建立o-xyz用戶坐標系，則根據標定的尺寸獲取每個標定點在用戶坐標系的坐標Pui=(xui，yui，zui)，i=1，2，3，…，n，n為標定點總數，如點P(0，3，0).再通過Pbi=Pui可得該特征點在機器人基坐標系下的坐標Pbi=(xbi，ybi，zbi)，i=1，2，3，…，n，n為標定點總數.其中用戶坐標系相對于機器人基坐標系的齊次變換矩陣可直接從機器人的示教器中讀出，是已知量.

3）求解手眼關系的齊次變換矩陣

設階梯形標定物上某一標定點P在線激光傳感器坐標系下的坐標為Ps(xs，0，zs)，在機器人基坐標系下的坐標為Pb(xb，yb，zb)，Ps通過式（6）轉換為Pb.

將式（6）展開為式（8）：

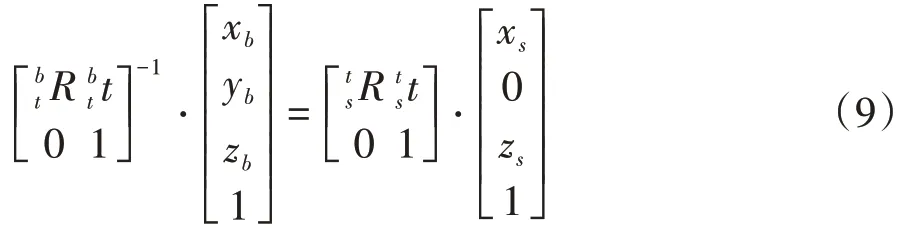
式（9）展開可得式（10）：

將式（10）展開可得式（11）：

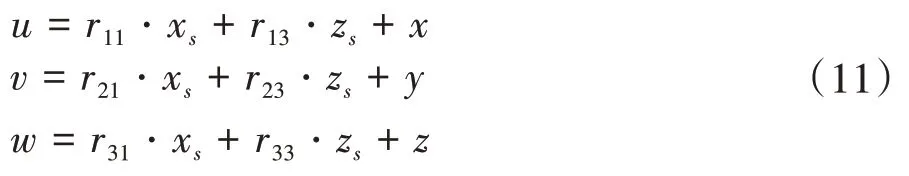
根據式（11）可知，該方程組存在9 個未知量，即r11，r13，r21，r23，r31，r33，x，y，z，而(Pb，Ps)構成的一組點可以確定三個約束方程，則解出式（11）只需要三組點；將式（11）轉化為式（12）：

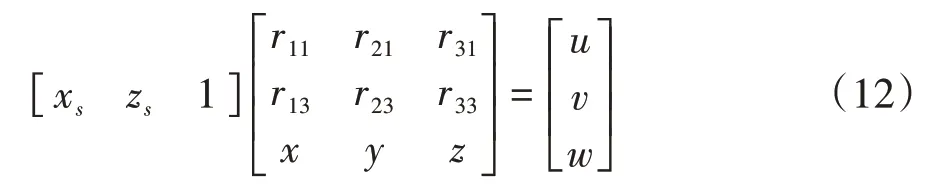
若特征點集Pnew中存在n個點，則將(Pbi，Psi)構成的n組點代入式（12）可得式（13）：

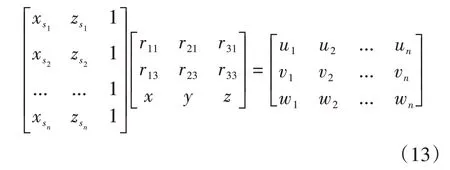
式（13）中，當n＞3 時，構成的矩陣方程不再是方陣，不存在解析解，此時利用最小二乘法求解矩陣方程的近似解，將式（13）簡寫為式（14）：

通過式（15）可解得9 個未知量，即r11，r13，r21，r23，r31，r33，x，y，z，剩下的未知量r12，r22，r32可通過向量叉乘計算得到，如式（16）所示：

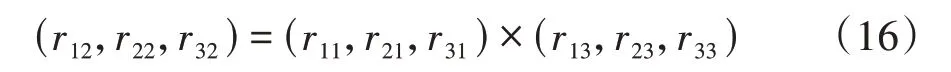
本節設計了一種階梯形標定物，并提出了一種線激光傳感器標定算法，該算法只需掃描一次標定物，提取階梯輪廓數據中的每個標定點，并利用RASANC 算法對標定點進行直線擬合，修正離群點；再通過用戶坐標系獲取標定點在機器人基坐標系下的坐標，最后利用最小二乘法解出手眼標定矩陣.

與球形標定物相比，本文僅需掃描一次階梯形標定物就可以快速計算出手眼標定矩陣，且無需對線激光傳感器所得的輪廓數據進行區域分割、圓形擬合等操作，計算量大幅度減少；同時，也不需要對標定點的y坐標額外計算，提高了標定結果的精度.

2 實驗與分析

2.1 實驗條件

本文實驗平臺的硬件環境和軟件環境如表1 所示.本文搭建的實驗平臺如圖8所示.利用球形標定法求解手眼標定矩陣后，控制機器人帶動線激光傳感器多位置、多姿態掃描實驗平臺上的任意點，同時記錄該點在機器人基坐標系下的坐標Preal_base，在線激光傳感器坐標系下的坐標Ptest_sensor，則Preal_base，Ptest_sensor構成實驗數據點集；再利用階梯形標定法求解手眼標定矩陣，重復上述步驟.

表1 實驗配置明細表Tab.1 Experimental configuration list

圖8 實驗平臺整體圖Fig.8 Overall diagram of the experimental platform

線激光傳感器固定在機器人末端執行器上，按照上述實驗步驟進行標定實驗，基于球形標定物的標定實驗如圖9 所示，基于階梯形標定物的標定實驗如圖10所示.

圖9 伯朗特機器人球形標定法實驗Fig.9 Experiment of Borunte Robot Spherical Calibration Method

圖10 伯朗特機器人階梯形標定法實驗Fig.10 Experiment on the stepped calibration method of the Borunte robot

2.2 精度分析

在解得手眼標定矩陣后，控制機器人帶動線激光傳感器掃描實驗平臺上的多個任意點，同時記錄每一個點在機器人基坐標系下的實際坐標Preal_base_i在線激光傳感器坐標系下的坐標Ptest_sensor_i，i=1，2，3，…，n，n為選取的點總數，(Preal_base_i，Ptest_sensor_i)構成實驗數據點集；再結合已求得的手眼標定矩陣，將傳感器坐標系下的坐標Ptest_sensor_i代入式（6）計算該點在機器人基坐標系的理論坐標Ptest_base_i，并計算出每一組點的Ptest_base_i與Preal_base_i的差值，利用差值評測球形標定法和階梯形標定法的實驗精度.

表2 左側為伯朗特機器人通過球形標定法解得手眼矩陣后，選取實驗平臺上任意5 點作為實驗點的實驗結果，并在實驗過程中標記選取的5 個點；表2 右側為伯朗特機器人通過階梯形標定法解得手眼標定矩陣后，帶動線激光傳感器掃描上述5 個標記點作為實驗點的實驗結果.

表2 伯朗特機器人手眼標定實驗結果Tab.2 Results of the hand-eye calibration experiments of the Bertrand robot

由表3 可知，球形標定法的最大誤差幾乎是階梯形標定法的兩倍，同時，球形標定法的平均誤差穩定在0.25 mm左右，而階梯形標定法的平均誤差穩定在0.15 mm左右，階梯形標定法的精度優于球形標定法，且可以滿足工業生產要求.

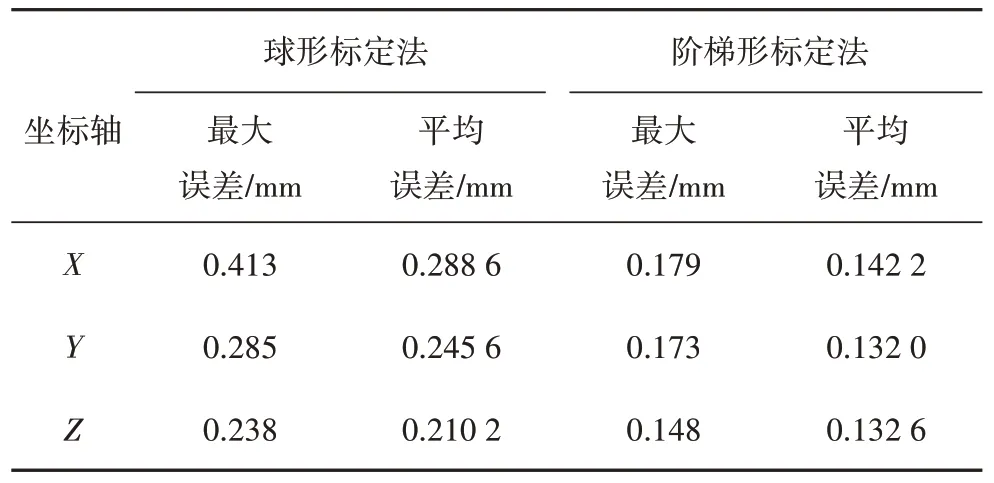
表3 伯朗特機器人手眼標定精度分析Tab.3 Accuracy analysis of hand-eye calibration of brunt robot

2.3 穩定性分析

在解得手眼標定矩陣后，控制機器人帶動線激光傳感器多位姿掃描實驗平臺上任一固定點P，獲取該點在線激光傳感器坐標系下的坐標Ptest_sensor_i，i=1，2，3，…，n，n為掃描總次數，再控制機器人末端執行器觸碰該固定點，并記錄點P在機器人基坐標系下的實際坐標Preal_base，(Preal_base，Ptest_sensor_i)構成實驗數據點集；再結合已求得的手眼標定矩陣，將線激光傳感器坐標系下的坐標Ptest_sensor_i代入式（6）計算該點在機器人基坐標系的理論坐標Ptest_base_i，并計算出每一組點Ptest_base_i與Preal_base的差值；為了更直觀地評估標定算法的穩定性，本文利用差值的3 倍標準差3δ評測球形標定法和階梯形標定法的穩定性.3δ越小，說明穩定性越強，反之，說明穩定性越差.本節對任一固定點P多位姿掃描5次分析穩定性.

伯朗特手眼標定穩定性分析如表4 所示.

表4 左側為伯朗特機器人通過球形標定法解得手眼標定矩陣后，選取點作為實驗固定點的實驗結果，實驗結果表明球形標定法的單坐標軸最大3 倍標準差在0.424 mm 左右；表4 右側為伯朗特機器人通過階梯形標定法解得手眼標定矩陣后，選取點P作為實驗固定點的實驗結果，實驗結果表明階梯形標定法的單坐標軸最大3 倍標準差在0.15 mm 左右.階梯形標定法的穩定性優于球形標定法，足以滿足許多復雜的工業現場要求.

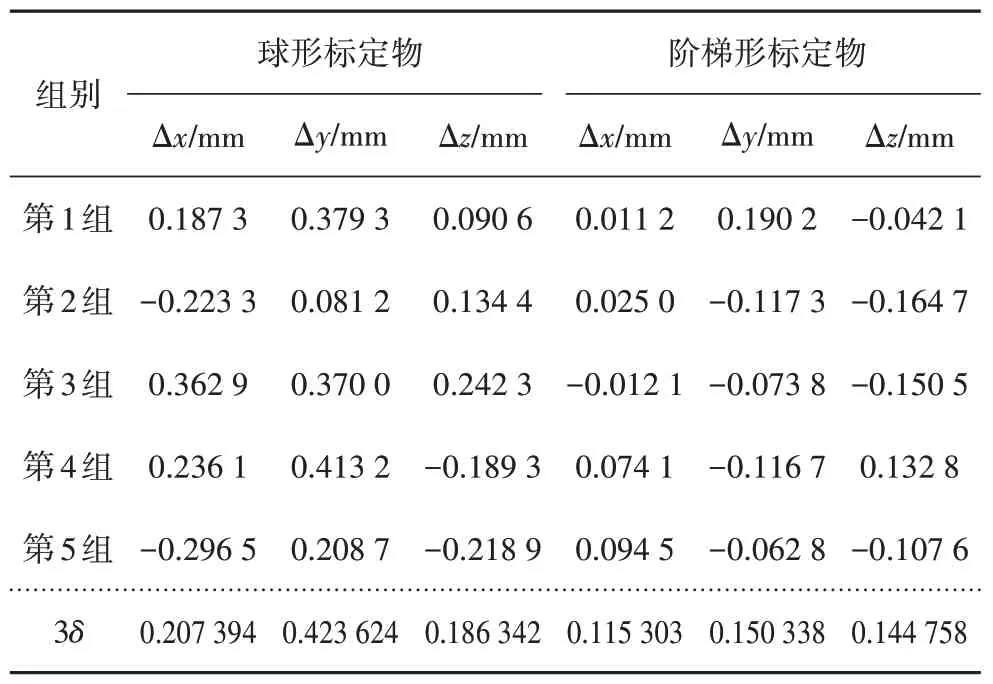
表4 伯朗特機器人手眼標定穩定性分析Tab.4 Stability analysis of hand-eye calibration of Bronte robot

2.4 算法復雜度分析

由實驗數據可知，本文的算法精度高于傳統的球形標定法；此外對比球形標定算法和本文算法的計算用時以表征算法的復雜度，用時少，說明算法復雜度低；反之，算法復雜度高.兩種算法的軟件實驗流程分別如圖11和圖12所示.

圖11 球形標定法實現流程Fig.11 The realization process of the spherical calibration method

圖12 階梯形標定法實現流程Fig.12 The realization process of the stepped calibration method

在同等情況下，對兩種算法各取5組點進行5次實驗，并計算5次實驗的平均耗時Tˉ，統計結果如表5所示.

表5 算法用時統計Tab.5 Algorithm time statistics

由表5 可知，傳統的球形標定法平均耗時在2.5 s 左右，而本文提出的算法平均耗時在0.474 s 左右，該方法顯著提高了算法速度，這對提高生產效率具有重大意義.

2.5 標定點集Pnew數量分析

從1.2.2 節可知，本文提出的標定算法求解手眼矩陣只需要3 組點，但精度一般較低；為保證測量精度和可靠性，本文采用數量不同n的組點，分別利用最小二乘法解得手眼矩陣；在解得手眼矩陣后，再進行精度分析和穩定性分析，尋找最優的組點數量，如圖13所示.

由圖13 和圖14 可知，組點數量n=4或5 時，其精度大小和穩定性基本為一恒值；當n＞5 時，實驗結果的精度和穩定性基本不變，但這樣會增加實操的復雜性；若無特殊需求，n=4或5 即可滿足實際工程需要，且性能較好.

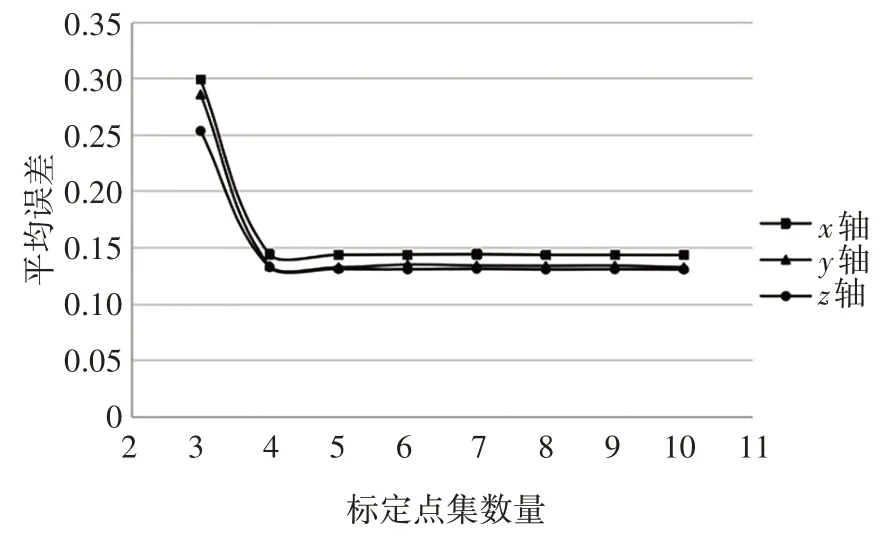
圖13 標定點集數量精度分析Fig.13 Precision analysis of the number of calibration fixed-point sets

圖14 標定點集數量穩定性分析Fig.14 Stability analysis of the number of calibration fixed-point sets

3 結論

針對基于球形標定物的手眼標定算法計算復雜度高，標定點坐標難以獲取且極易出錯的問題，本文設計了一種階梯形標定物，并基于階梯形標定物提出了一種手眼標定算法，該算法只需要線激光傳感器掃描一次標定物即可獲取標定點在線激光傳感器坐標系下的坐標，并使用RANSAC 算法擬合標定點，再根據這些標定點在機器人基坐標系下的坐標構建手眼方程.階梯形標定方法求解過程簡單，便于實際應用.實驗結果表明，階梯形標定物的精度和穩定性均優于球形標定法，階梯形標定法的標定精度在0.1 mm左右，可以滿足工業上的大部分應用.