求解最小支配集的線性混合整型規劃算法

程詠鋒，吳歆韻，熊才權

(湖北工業大學計算機學院，湖北 武漢 430068)

最小支配集問題為NP難問題，是一類重要的組合優化問題。對于最小支配集問題的求解不可能出現多項時間精確算法。最小支配集問題及其各種拓展問題在多文檔摘要[1]，社會網絡的建模和研究[2]，通信網絡[3]等諸多領域具有廣泛的應用。

目前，求解最小支配集問題精確算法均為非多項式時間算法，Fomin F V[4]等提出一種分支簡化(FKW)算法，盡管最早突破O(2n)界限,但FKW仍難令人滿意,如果圖中沒有低于2度的節點,算法將回歸平凡的枚舉。Grandoni F[5]等人提出了求最小支配集的Grandoni算法，但該算法只能求最小支配集的大小，不能求具體的最小支配集；Lu gang[6]等對該算法提出了修改，應用于求解具體的最小支配集；Headar[7]等提出一種混合遺傳算法，與局部搜索算法相結合，設計出特定的適應度函數求解最小支配集，該算法在文獻[8]中得到改進。David[9]等針對大型圖的最小支配集問題，提出一種新的基于順序的隨機局部搜索算法。Zhu X[10]提出求解最小支配集的多項式時間近似方案，但這些算法不能在一般圖上得到應用。Yuan Fuyu[11]通過分析大規模實例，結合支配集問題的特點提出一個快速高效地求解最小支配集問題的算法(Fast MDS)，其他最小連通支配集算法參見文獻[12-14]。

本文根據最小支配集問題的性質，構造出一種求解該問題的數學模型，采用java語言實現鄰接支配矩陣的存儲和根據數學模型利用Gurobi優化器進行線性求解，并與文獻[6]提及到的FKW算法，Grandoni算法和改進的Grandoni算法在當前國際文獻公開的共74個算例上進行比較，該算法的計算效率明顯優于其它的精確算法，并且在所有算例上都能得到較好的精確解。

1 最小支配集問題的描述

1.1 問題定義

對于無向不連通圖G=(V,E)，圖G的頂點集合為V=V(G)，圖G的邊集合為E=E(G)。若頂點集合V當中存在一個子集D?V,對于集合V當中的任意一個頂點Vp，要么Vp∈D，要么Vp與集合D當中某個頂點相鄰，則將集合D稱為圖G=(V,E)的一個支配集。當集合D當中任意一個真子集都為非支配集時，則稱集合D為圖G的一個極小支配集。

設集合D是圖G=(V,E)的一個支配集，當圖G當中不存在任何一個支配集D1，使得|D1|<|D|，此時的集合D稱為圖G=(V,E)的一個最小支配集，圖G當中所有最小支配集的大小稱為圖G=(V,E)的支配數，表示為γ(G)。

以下給出最小支配集問題的相關定義:

定義1 支配集(Dominating Set)：集合D?V(G)，若任意的Vp∈V(G)-D，存在一個頂點Vq∈D，使得頂點Vp與頂點Vq之間有邊相連，滿足這樣條件的集合D就構成了圖G的一個支配集,簡記為DS。

定義2 極小值支配集(Minimal DS)：設集合D為圖G=(V,E)的一個支配集，當集合D當中的任意一個真子集都無法構成圖G=(V,E)的一個支配集，則稱集合D為圖G=(V,E)的一個極小支配集。

定義3 最小支配集(Minimum DS)：在圖G=(V,E)的所有支配集當中，頂點個數最少的那個支配集稱為圖G=(V,E)的最小支配集。簡稱MDS。

由相關支配集的定義可知極小支配集和最小支配集的相關性質：

1)對于一個任意的非空圖G=(V,E),可以找到若干個極小支配集，這些極小支配集的階(頂點數)不一定相同。

2)對于一個任意的非空圖G=(V,E)，可以找到若干個最小支配集，這些最小支配集的階(頂點數)一定相同。

3)如果一個集合X，滿足最小支配集的條件，那么集合X一定滿足極小支配集的條件；反之，若集合X滿足極小支配集的條件，那么集合X未必滿足最小支配集的條件。

1.2 整數規劃模型

最小支配集問題指的是對于給定的圖G=(V,E)，在集合V中找到一個支配集D,使得支配集D中所含節點的個數達到最小。通過引入n維0-1向量X=(x1，x2，x3，…，xn)，xp=1表示頂點p∈D，xp=0表示頂點p?D，則最小支配集的整數規劃模型可以描述為式(1)-(4)：

(1)

s.t.

(2)

(3)

(4)

四個公式分別表示為：1)f(X)作為目標函數表示以最少的頂點集合作為支配點，2)為約束條件表示任意一個頂點Vp要么是支配點，要么被支配集和當中的點所支配，n表示圖頂點的個數。3)LP,q為常量，表示第p節點是否可以與第q節點互相支配，是則為1，否則為0。4)變量xp表示是否選取第p個節點作為最小支配集，是則為1，否則為0。

2 圖的最小支配集的多項式方程組模型與Gurobi求解器求解

Gurobi是由美國Gurobi公司開發的新一代大規模優化器，綜合能力強，性價比較優。它支持Windows,Linux,MacOSX等多種平臺,采用了 最新的優化技術,充分利用多核處理器優勢,支持并行計算;問題尺度只受限制于計算機內存容量,不對變量數量和約束數量有限制;提供了方便輕巧的Java接口;能夠快速高效地解決大規模線性問題、二次型目標問題、混合整數線性和二次型問題等數學問題。

設圖G=(V,E)是無向圖，則圖G的鄰接矩陣定義為A=[vpq]n×n，其中

(1)

通常將A的第i行記為Ai，1≤i≤n。此外在此基礎上定義鄰接支配矩陣

A*=[vpq]n×n

其中

(2)

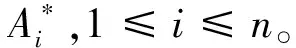
對于給定具有n個頂點的無向圖G=(V,E)，其鄰接支配矩陣為A*=[vpq]n×n。由最小支配集的定義可知，求解一個多元多項式方程組的0-1解與求解圖G的最小支配集這兩個問題是等價的，即n維向量X中所含1的個數達到最小。

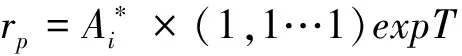
(3)

設n維向量Xk=(x1，x2，x3…xn)expT,若該n維向量滿足(Ck)的所有不等式，故向量Xk是方程組(Ck)的一個解。則其中取值為1的變量所對應的頂點構成的集合為支配點集合，取值為0的變量所對應的頂點構成的集合為被支配點集合。

通過Java語言實現無向圖的支配矩陣存儲，設置最優化模型的系數列表，調用Gurobi優化器進行優化求解。首先使用grbModel.addVar函數構建目標函數系數列表；其次使用grbModel.addConst構建約束條件的系數列表；最后使用grbModel.setObjective函數優化求解。利用公共線性規劃求解器對其進行求解, 使得目標函數值不斷減小，最終可求得一個最小的k值。

3 實驗結果與分析

本節主要是對求解最小支配集的MILP算法的性能進行實驗分析。并與文獻[6]提及到的FKW算法和Grandoni算法以及改進的Grandoni算法在當前國際文獻公開的共74組算例上進行比較。第一組算例為文獻中作者[15]隨機生成的大規模算例。第二組算例，包含廣泛的真實圖，研究于許多領域，特別是在圖染色問題上[16]。

實驗環境:本次實驗所涉及的算法均以Java語言進行編程實現, 測試運行的 PC 機運行環境為 Core i5 3.4 GHz CPU 和 8.0 GB RAM, 操作系統為 Windows 10,JVM 為 Oracle JRE 1.8。為了驗證算法的性能,采用兩組算例進行實驗驗證。

3.1 隨機算例的測試

第一組算例為隨機生成的24組小規模算例，算例生成方法為：在一個N×N的固定區域中隨機選取一定數量的節點作為算例的圖節點；當區域內的兩節點p，q之間的距離小于某個設定的常數k值時，將{p，q}作為算例圖中的一條邊，即兩節點p，q之間相互連通。該組隨機算例節點數從20-120，每組算例運行10次，求出最優解的時間并取平均值，結果見表1。表1前兩列分別表示算例的名稱和最小支配集個數，其余列表示每個算法運行10次找到最小支配集個數時所需要的平均時間。

表1 隨機算例對比 s

圖1為表1的信息匯總。通過圖1，可以明顯看到，求出24組小規模算例的最小支配集，FKW算法用了16.239 s，Grandoni算法用了1257.115 s，改進的Grandoni算法用了1217.891 s，而提出的MILP算法給出了2.674 s的最好結果，根據在隨機生成的24組小規模算例上的結果，MILP算法具有更好的性能。

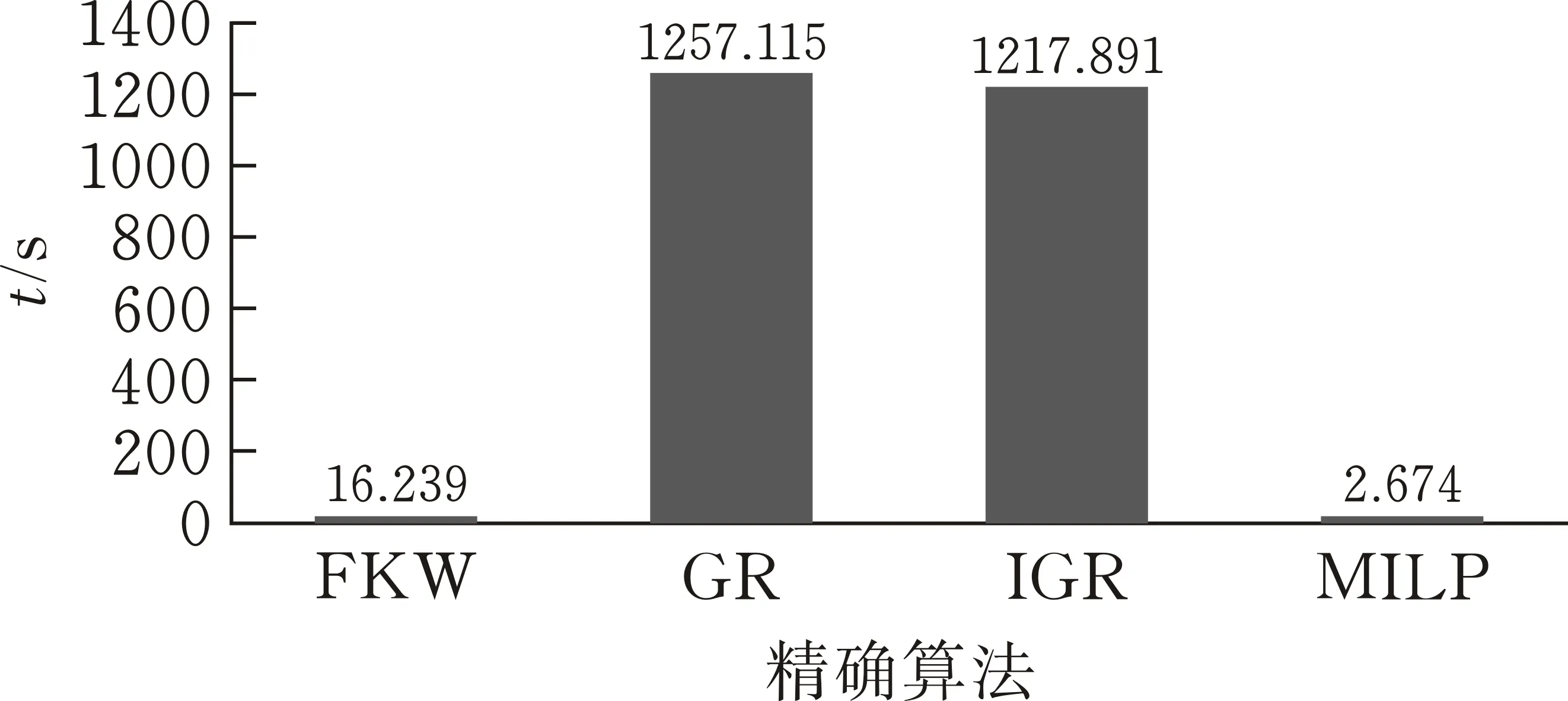
圖 1 精確算法的總耗時

3.2 圖著色算例測試

由于第一組圖的最小支配集較小，實驗結果具有局限性。因此對第二組圖進行測試，這個測試涉及到寬面圖，該50組算例頂點規模從11到864個頂點不等，這些算例已經在許多研究中使用，特別是在圖著色的問題上。這次測試包含50組算例，每組算例運行10次，測試結果見表2。

在圖著色算例上的測試結果見表2，前四列分別表示算例的名稱，頂點個數，邊數，最小支配集個數，后四列分別表示FKW算法，GR算法，IGR算法，以及MILP算法求出最優解所需花費的時間。“-”表示未能給出最優解，“>3600”表示程序運行時間超過一小時，表3是表2的匯總，顯示了各算法在1小時內成功求出最優解算例的個數。

從表2的結果可以看出，對于復雜算例的計算，IGR算法的性能要優于GR算法，FKW算法在計算時會造成程序崩潰。在除Le450-5c外的所有算例上，MILP算法對于其余49個算例均能在一小時內找到最優解。通過表3的匯總可以看出，對比其他三個算法，MILP算法在一小時的計算時間內成功率達到98%，在所有算例上MILP算法的求解速度均快于其他算法，并且對于比較復雜的算例，MILP算法求解的速度更快，這些數據表明，MILP算法是求解最小支配集問題的一種高效的精確算法。

表2 圖著色算例對比

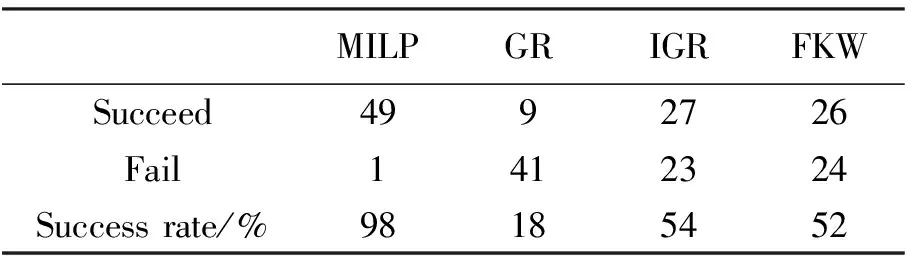
表3 圖著色算例結果匯總

4 結論

本文提出了一種求解最小支配集問題的線性混合整數規劃算法,在MILP算法中，根據最小支配集問題的特點，提出一種新的整數規劃模型，將該問題轉化為線性規劃問題，運用Gurobi求解器進行線性求解。采用當前國際文獻公開的共74組算例作為算法測試實驗集，在與文獻中介紹的其他精確算法進行比較后發現，MILP算法在中小規模的算例上能夠以較快的時間求出最優解，對于較為復雜的算例，MILP算法都能求出最優解，并且在計算出最優解的時間上具有明顯優勢。