大型儲罐頂部抗風圈設計方法對比和優化*

倪恒 陳嚴飛，2 馬尚 董紹華

1中國石油大學（北京）·油氣管道輸送安全國家工程實驗室·城市油氣輸配技術北京市重點實驗室

2大連理工大學·工業裝備結構分析國家重點實驗室

儲罐大型化是當前儲罐發展的趨勢[1]，但容積越大的儲罐抵抗風載荷的能力越差，而我國原油儲庫大多坐落在沿海地域，儲庫中的大型儲罐易在臺風等極端天氣的作用下屈曲失穩（圖1），故需對儲罐的抗風能力進行加強。目前主要采用加大壁厚和增設抗風結構兩種方法，其中，單純通過增加儲罐壁厚的方式來提高屈曲載荷因鋼材成本和焊接工藝等因素受到限制[2]，而在儲罐罐壁中上部增設抗風圈較前者可以在原有壁厚的基礎上提高儲罐的抗風性能，故抗風圈的合理設計與安裝顯得尤為重要。

圖1 儲罐在颶風下的整體屈曲Fig.1 Overall buckling of the tonk under the hurricane

我國大型儲罐抗風圈設計通常參照GB 50341設計規范以及美國石油學會API 650 設計規范，上述兩種規范中抗風圈的設計方法存在差異[3]，國內一些學者認為，相較于API 650 設計規范，使用GB 50341 設計的大型儲罐抗風圈更為保守。李玉坤[4]使用有限元模擬軟件對儲罐強度和穩定性進行仿真分析，認為使用API 650 設計的抗風圈更加穩定且節省材料。李良平[5]在比較了GB 50341 和API 650 標準之后，認為使用API 650 標準設計的抗風圈具有更好的經濟效益。GB 50341 設計方法過高的保守性導致抗風圈設計尺寸偏大，抗風圈性能沒有得到充分利用，李宏斌[6]建議參考API 650 以及BS 2654 的抗風圈設計規定，當儲罐實際直徑大于60 m 時，抗風圈截面模數計算公式中的設計直徑仍按照60 m 進行計算，能起到節省鋼材和方便施工的作用。李玉坤和孫文紅[4]建議將我國規范中抗風圈截面模量公式中的風載荷標準值替換為基本風壓以降低其保守性，這條建議在GB 50341—2014中得到了采納。此外，國外學者針對抗風圈設計也展開了相關研究，BRIASSOULIS 和PECKNOID[7]對三個風載荷作用下的加強筒倉進行分析后指出，罐壁和抗風圈之間的相互作用會產生較大的周向應力。BU 和QIAN 認為[8]，API 650 中所采用的二維簡化力學模型沒有考慮底部約束的加強效果，導致大型儲罐抗風圈過于保守。

大多數學者經實驗觀測及理論分析后認為，現有規范中大型儲罐抗風結構設計方法過于保守，需提出合適的方法降低保守性。針對此問題，本文參考API 650 規范中降低保守性措施開展對GB 50341抗風圈截面模量計算公式中設計直徑上限的研究，對頂部抗風圈設計方法提出了優化的建議，并建立有限元模型進行屈曲分析加以驗證。

1 現行規范頂部抗風圈設計方法

1.1 GB 50341 設計方法

GB 50341 選用的簡化力學模型特征為：儲罐只有迎風面中心子午線周圍的60°區域受風載荷作用；作用于罐壁的風壓大小符合正弦分布且方向垂直于罐壁表面。儲罐受風載荷作用問題便簡化成為了一個圓拱段在方向受正弦分布外力作用的平面問題，簡化力學模蓴如圖2 所示。

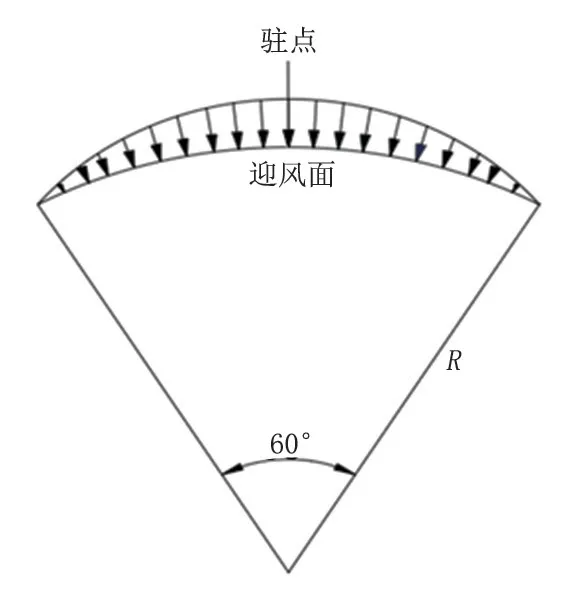
圖2 GB 50341 簡化力學模型Fig.2 Simplified mechanical model of GB 50341

假設儲罐上部承受的風載荷全由抗風圈承擔，最大彎矩出現在圓拱中心（駐點位置），其大小為

式中：Mmax為最大彎矩，N·m；K1為體型系數，取1.5；K2為風壓高度變化系數，取1.15；ω0為基本風壓，Pa；H為儲罐高度，m；R為儲罐半徑，m。

最小截面模量計算公式為

式中：Z為頂部抗風圈最小截面模量，mm3；[σ]為材料的許用應力，取210 MPa。

合并公式（1）、（2），代入相關數據并向上取整后得到與基本風壓值，儲罐幾何尺寸相關的最小截面模量計算公式為

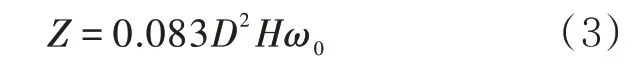
式中：D為儲罐直徑，m。

1.2 API 650 設計方法

ADAMS[9]給出了一種API 650 抗風圈尺寸設計公式的推導方法，其簡化力學模型是將Roark 圓環公式中的應力情況8 和情況20 相結合（w為均布單向荷載，kPa），如圖3 所示。

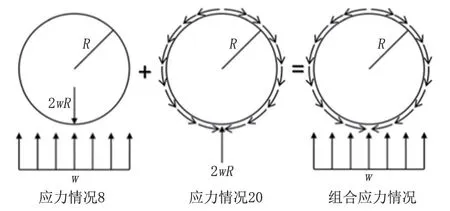
圖3 Roark 圓環公式情況8 和情況20 的組合示意圖Fig.3 Combination diagram of Case 8 and Case 20 by Roark ring formala

組合情況下的最大彎矩是均勻線性載荷和環半徑的函數。

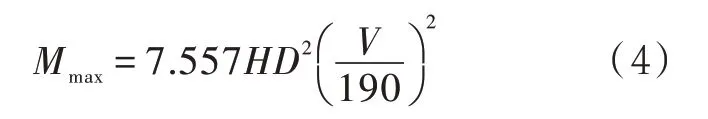
式中：V為設計風速（3 s 陣風），km/h。

抗風圈所需最小截面模量計算公式為

式中：φ為應力因子，取0.625；σ為材料的許用應力，取207 MPa。

通過上述計算得到式公（6），即最小截面模量計算公式為

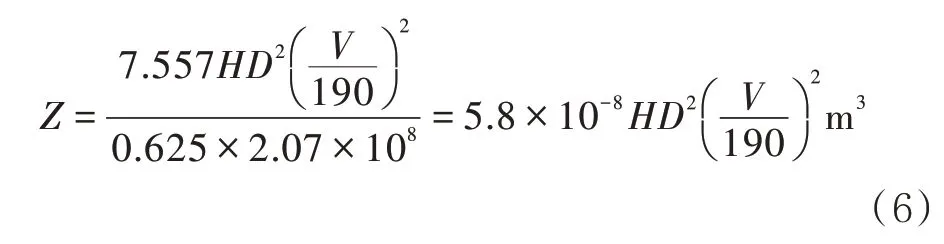
1.3 兩種設計方法對比

結合上述內容可以看到，API 650 和GB 50341中頂部抗風圈的設計思路相同，兩種規范均使用最小截面模量來表征抗風圈尺寸，相關計算公式形式相似但具體參數不同，這主要是由基本風速（時距）以及選用的簡化力學模型等因素的不同而導致的。GB 50341 使用基本風壓ω0來表征風載荷的大小，而API 650 則使用設計風速V來表示，但兩者本質并無區別。

從上述設計方法推導過程可以看出，兩種頂部抗風圈設計方法均存在過于保守的不合理之處：GB 50341 所使用的簡化模型假設風載荷僅作用于駐點周圍60°內的罐壁之上，荷載大小使用正弦函數來表示，API 650 所使用的簡化模型假設風載荷為單側均布風荷載和均勻剪切荷載的結合，這些假設與儲罐周圍的實際風場并不一致[10-11]；API 650和GB 50341 皆要求上部罐壁的風荷載全部作用在抗風圈上，并未考慮中間加強圈和罐底對于上部罐壁的加強作用。大型儲罐作為一種薄殼結構，完全忽略抗風圈、加強圈、罐底之間的相互加強作用并不合理。

API 650 規定，對于直徑大于61 m 的儲罐，經買家和制造商協商后，抗風圈最小模量計算公式中不需要使用儲罐的實際直徑，而是使用61 m 來代替。對于更加保守的GB 50341 而言，設計大型儲罐頂部抗風圈時仍需要探索一種更經濟的抗風圈設計直徑上限。

2 頂部抗風圈設計優化

2.1 方案研究

為了降低大型儲罐頂部抗風圈的保守性，提升經濟性，建議使用55 m 作為GB 50341 規范頂部抗風圈的設計直徑上限，采用有限元分析對其安全性進行驗證，具體方案如下：

對4 個實際尺寸的儲罐進行有限元建模（表1），設計頂部抗風圈時限制其最大設計直徑為55 m，即對直徑大于55 m 的儲罐，頂部抗風圈截面模量計算公式中設計直徑的取值全部用55 m 進行替代，而加強圈仍按照GB 50341 的要求進行設計。依次對4 個儲罐進行線性屈曲分析和含有初始缺陷的幾何非線性分析，薄殼結構具有很高的初始缺陷敏感性[12]，故只要非線性分析結果表明屈曲載荷大于設計風壓，則證明儲罐設計是安全的。

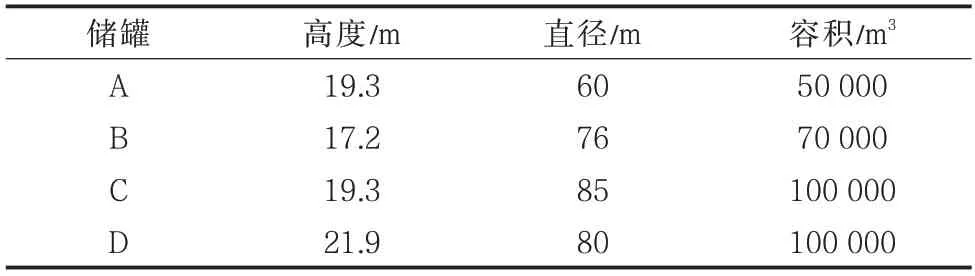
表1 模型儲罐尺寸Tab.1 Size of model tanks

2.2 有限元模型

采用以上儲罐幾何尺寸對儲罐建立有限元模型建立，模型罐壁厚度計算應采用變設計點法[13]，假定儲罐所用板材材料為鋼，模型材料楊氏模量為206 Pa(G)，泊松比為0.3。建立模型時考慮抗風圈和加強圈，頂部抗風圈的截面模量取直徑55 m，各儲罐頂部抗風圈設計相關參數見表2，類型為GB 50341 規范中的類型（e），截面形狀如圖4 所示，其中t為最上層儲罐壁的厚度（mm），b為頂部抗風圈的寬度（mm）。儲罐A 的加強圈尺寸（單位mm）為L200×125×12，其余3 個儲罐的加強圈尺寸為L200×200×14，加強圈的位置和個數參照規范設計。有限元模型的邊界條件為：儲罐為空罐且不考慮罐壁附件影響；約束儲罐底板的徑向位移及切向位移，防止儲罐發生剛體運動；施加風壓載荷時僅考慮風壓的周向分布[14]，但儲罐迎風面、側面、背面的風載荷分布形式直接影響屈曲載荷大小。為了有限元結果更加準確，采用RISH[15]提出的風壓分布函數（公式7）模擬儲罐四周的真實風壓。風載荷分布示意圖見圖5，建立的儲罐有限元模型見圖6。

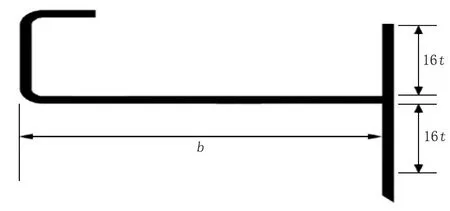
圖4 設計中所采用抗風圈的截面形狀Fig.4 Cross section shape of wind girder used in the design

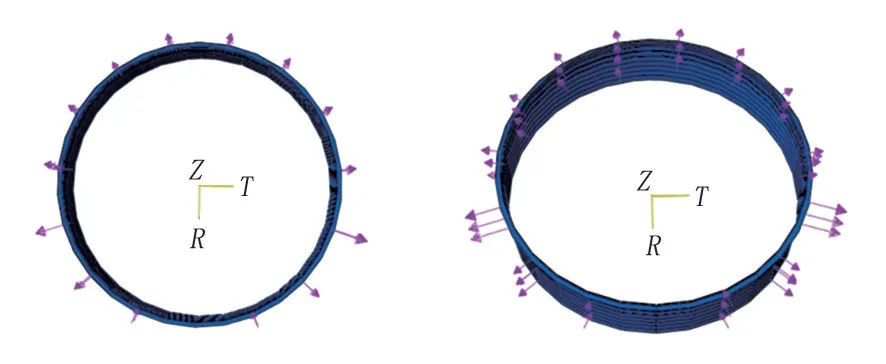
圖5 風載荷分布示意圖Fig.5 Wind load distribution schematic diagram

圖6 儲罐有限元模型Fig.6 Finite element model of tanks

表2 頂部抗風圈設計相關參數Tab.2 Design parameter of top wind girder

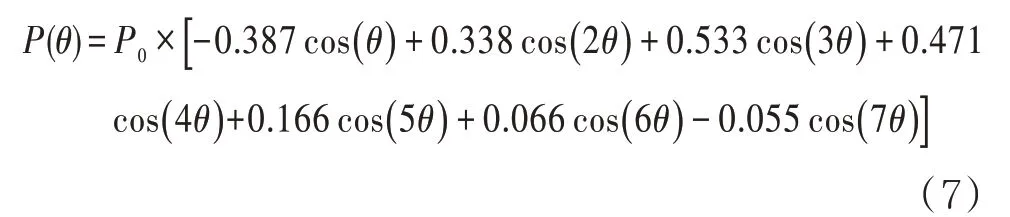
式中：θ為周向角，(°)；P(θ)為周向角θ處的風壓，Pa；P0為駐點處風壓，Pa。

2.3 有限元分析結果

利用屈曲分析對建立的4 個儲罐有限元模型的屈曲模態和特征值進行求解，得到的結果如圖7 和表3 所示。

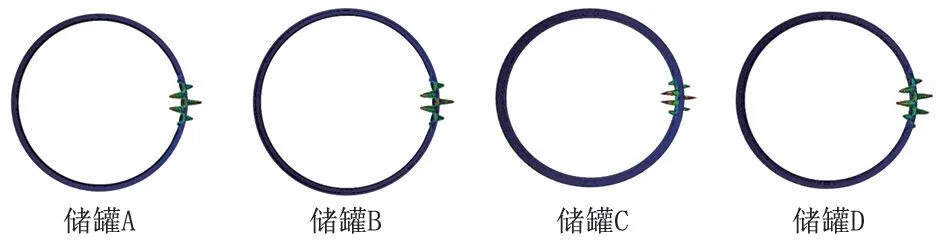
圖7 第一階屈曲模態示意圖Fig.7 First-stage buckling mode schematic diagram

表3 特征值屈曲載荷分析結果Tab.3 Analysis results of eigenvalue buckling load Pa

在特征值屈曲分析的基礎上對上述儲罐模型進行含初始缺陷的非線性屈曲分析，初始缺陷大小分別為0.1t，0.25t，0.5t，0.75t和1t。采用弧長法對載荷施加過程中儲罐某一固定位置的載荷大小及徑向位移進行跟蹤，得到的載荷-位移曲線如圖8 所示，圖中水平軸為使用最上層罐壁厚度t歸一化后的徑向位移w，縱軸為使用特征值屈曲分析得到的屈曲壓力載荷P(LBA)歸一化后的施加載荷P，水平虛線表示特征值屈曲荷載P(LBA)，其歸一化值為1.0，紅色實線表示歸一化后的設計壓力。

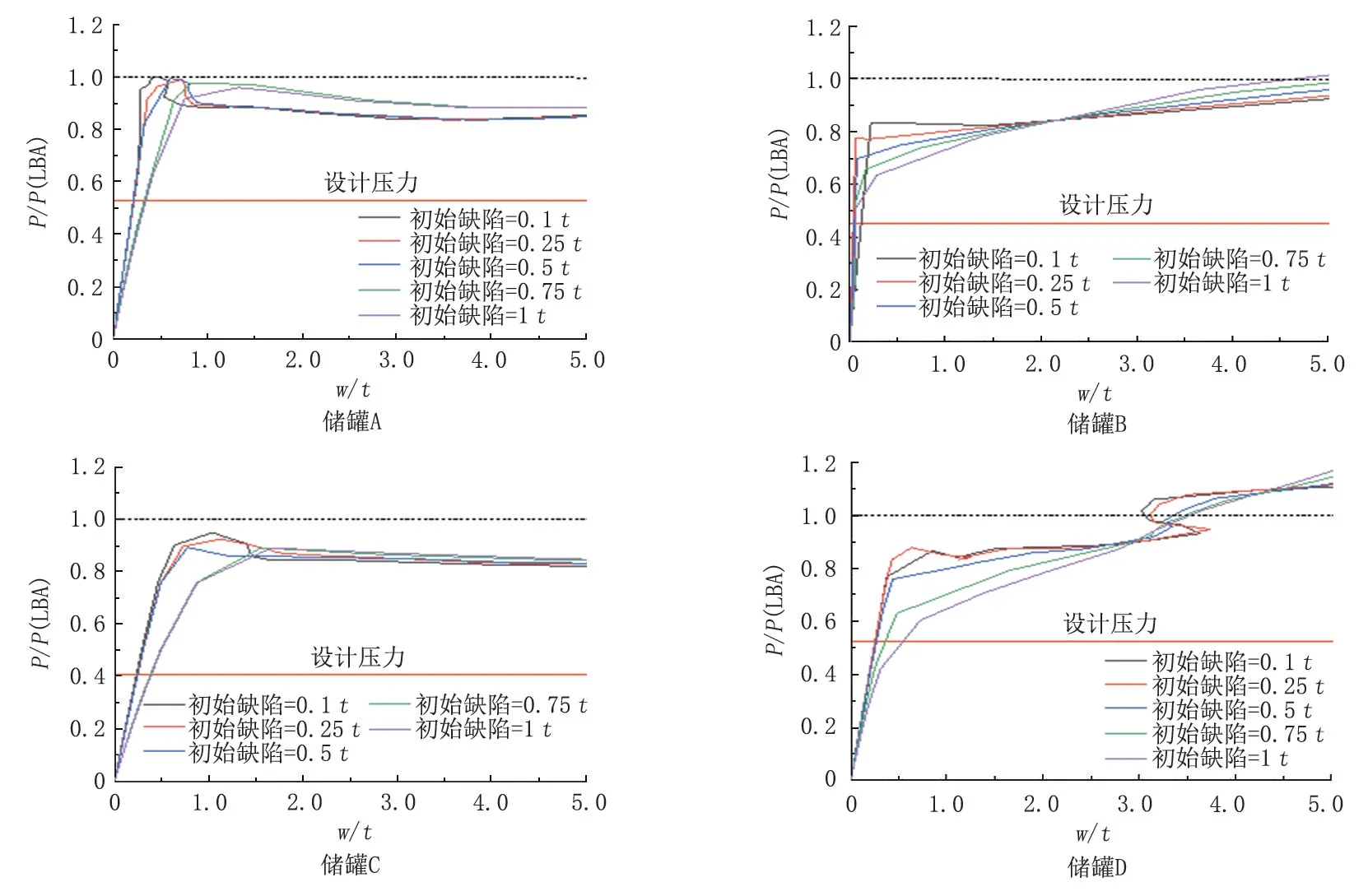
圖8 含初始缺陷的非線性屈曲分析結果Fig.8 Result of nonlinear buckling analysis with initial imperfections

從圖8 可以看出：在載荷施加初始階段，隨著載荷P的增大，徑向位移增長較小，而后續徑向位移從某點開始急劇增大，這表明儲罐開始屈曲，此時該點對應的載荷P即非線性屈曲載荷。4 個儲罐在不同初始缺陷下的非線性屈曲荷載都大于設計風壓，這表明直徑為55 m 的儲罐設計的頂部抗風圈足以保持儲罐頂部邊緣的圓度，能有效防止儲罐整體屈曲。改進后的頂部抗風圈截面模量計算公式為

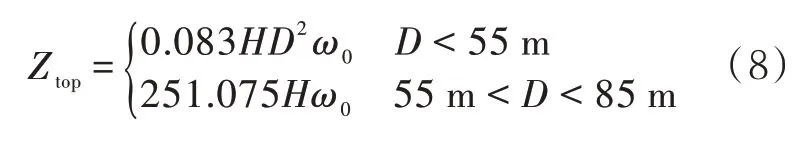
3 結論

頂部抗風圈是增強儲罐抗屈曲能力的重要結構，但當前儲罐設計規范中關于頂部抗風圈尺寸設計過于保守。針對此問題，闡述了兩種規范中頂部抗風圈截面模量計算公式的推導過程，分析了GB 50341 和API 650 規范中不同的頂部抗風圈設計方法保守性的來源，提出了新的尺寸設計建議，并通過有限元計算進行了驗證，得到以下主要結論：

（1）相較于API 650，GB 50341 關于頂部抗風圈的設計方法更加保守且缺少降低保守性的措施。

（2）GB 50341 和API 650 規范中頂部抗風圈設計保守性有兩個主要來源：①簡化力學模型中風荷載的分布形式與真實風壓分布并不一致；②推導過程中都忽略了不同結構之間的相互加強作用。

（3）圓柱薄殼結構具有高度的缺陷敏感性，含有初始缺陷的儲罐其屈曲載荷會隨著引入初始缺陷比例的增大而減小。

（4）對于直徑大于55 m 小于85 m 的儲罐，計算頂部抗風圈截面模量時，設計直徑取55 m 可以在保證安全的前提下節省儲罐的建造成本。