大數(shù)模乘硬件模塊的研究與實(shí)現(xiàn)*

段曉毅 黃 燁 曹佳樂(lè)

北京電子科技學(xué)院,北京市 100070

1 簡(jiǎn)介

RSA、ECC(Elliptic Curve Cryptography)算法是常用的公鑰算法,而素?cái)?shù)域上的模乘運(yùn)算[1]是公鑰加密算法中的基礎(chǔ)算法。 但在密碼體系的運(yùn)算中,其運(yùn)算操作數(shù)一般是任意大整數(shù),即位數(shù)為256 bit 或以上的數(shù)據(jù)結(jié)構(gòu),算法復(fù)雜度較大,已經(jīng)成為影響當(dāng)前公鑰加密體系發(fā)展的重要問(wèn)題。 素?cái)?shù)域中的模乘算法是最費(fèi)時(shí)的計(jì)算,所以為了提升公鑰密碼系統(tǒng)的計(jì)算效率,選擇計(jì)算速度快、資源耗費(fèi)少的高效硬件模塊非常重要[2]。

當(dāng)前國(guó)內(nèi)外對(duì)于大數(shù)模乘問(wèn)題的研究方案大致可分為兩種:第一種即利用各類基本算法及其改進(jìn)算法,通過(guò)算法結(jié)構(gòu)構(gòu)建對(duì)應(yīng)的硬件電路,實(shí)現(xiàn)大數(shù)模乘功能,例如加法型算法[3]、估商型算法[4]、蒙哥馬利算法,其中又以蒙哥馬利型算法應(yīng)用范圍最廣,相繼提出多種改進(jìn)方式,實(shí)現(xiàn)效果良好。 另一種則從硬件結(jié)構(gòu)出發(fā),對(duì)于硬件架構(gòu)進(jìn)行重構(gòu),高效利用計(jì)算資源,提升模乘計(jì)算速度[5],以FPGA 細(xì)粒度映射技術(shù)為例[6],此在各類硬件載體上都有相關(guān)運(yùn)用,例如通過(guò)加密智能卡實(shí)現(xiàn)[7]。

大數(shù)模乘在基礎(chǔ)研究以及密碼學(xué)等領(lǐng)域都有大量應(yīng)用,特別是在公鑰密碼算法方面[8]。模乘通常情況下表示為:C =(A × B)mod N,其中A、B、N 都為k bit 二進(jìn)制的大整數(shù)。 模乘運(yùn)算由基本的乘法和計(jì)算余數(shù)的模運(yùn)算簡(jiǎn)化組成,目前主要的運(yùn)算形式有先計(jì)算乘法后再進(jìn)行模簡(jiǎn)化運(yùn)算,以及一邊進(jìn)行乘法同時(shí)進(jìn)行模簡(jiǎn)化運(yùn)算這兩大類基本實(shí)現(xiàn)方式[9]。

若以更細(xì)化、更精準(zhǔn)的處理方式來(lái)劃分大數(shù)模乘的處理流程的話,大數(shù)模乘算法又可分為加法型算法、估商型算法、蒙哥馬利型算法這三大類。 蒙哥馬利型模乘算法是目前在硬件結(jié)構(gòu)上用于快速實(shí)現(xiàn)模乘計(jì)算最適合的算法。 本文改進(jìn)了蒙哥馬利算法并將其實(shí)現(xiàn)。

2 改進(jìn)的蒙哥馬利模乘算法

蒙哥馬利模乘算法是蒙哥馬利在1986 年所提出的一種算法[10],主要是為了解決大整數(shù)模冪運(yùn)算問(wèn)題。 由于模冪與模乘運(yùn)算可以互相轉(zhuǎn)換,蒙哥馬利模乘算法把部分積對(duì)任意的n 取模運(yùn)算轉(zhuǎn)化為對(duì)與n 互素的數(shù)基R 進(jìn)行取模,通常都選R=2k,k 是非負(fù)整數(shù)。 由于R 比n 小得多,對(duì)數(shù)基R 的取模運(yùn)算要比對(duì)n 的取模運(yùn)算簡(jiǎn)單得多[11],所以蒙哥馬利模乘算法在RSA 密碼算法的研究中得到廣泛的應(yīng)用。

定義模乘算法為MM(x,y),如果模數(shù)m 是素?cái)?shù),且滿足m>2,則存在一個(gè)元素2-1∈Fm,使得2 × 2-1mod m =1。 假設(shè)m 是一個(gè)k bit 位的素?cái)?shù),那么可以選擇一個(gè)數(shù)R,使得R = 2k且滿足x,y∈Fm其中x可表示為:

將式(2.1) 代入模乘計(jì)算表達(dá)式,得到下式:

由于基本的蒙哥馬利模乘算法中不但包含基本的乘法、加法運(yùn)算,還包含了模逆運(yùn)算,并不利于計(jì)算機(jī)的硬件實(shí)現(xiàn)。 改進(jìn)的蒙哥馬利模乘算法通過(guò)對(duì)基本算式的重新表達(dá),配合數(shù)論里的基本結(jié)論,巧妙避免了復(fù)雜運(yùn)算,易于模乘計(jì)算[12]。

由數(shù)論知識(shí)可知用一個(gè)自然數(shù)去乘2-1有以下結(jié)論:

將式(2.2)中單次運(yùn)算括號(hào)中的部分套用式(2.3),即可得到改進(jìn)后的蒙哥馬利模乘算法[13]MM(x,y),其算法流程如下所示:

改進(jìn)后的蒙哥馬利模乘算法結(jié)構(gòu)簡(jiǎn)單,易于硬件描述實(shí)現(xiàn),本文就以改進(jìn)的蒙哥馬利模乘算法MM(x,y) 為設(shè)計(jì)基礎(chǔ),實(shí)現(xiàn)蒙哥馬利型大數(shù)模乘模塊功能。

3 蒙哥馬利型大數(shù)模乘模塊的總體設(shè)計(jì)

3.1 蒙哥馬利型大數(shù)模乘模塊外部總視圖

本方案中的大數(shù)模乘模塊的外部總視圖如圖3-1 所示:

圖3-1 蒙哥馬利型大數(shù)模乘模塊外部總視圖

輸入:x、y、m

輸出:C

x:參與模乘運(yùn)算的乘數(shù)1,輸入范圍從1bit-4096bit。

y:參與模乘運(yùn)算的乘數(shù)2,輸入范圍從1bit-4096bit。

m:參與模乘運(yùn)算的模數(shù),輸入范圍從1bit-4096bit。

C:模乘的輸出結(jié)果, 輸出范圍從1bit-4096bit。

對(duì)于本文系統(tǒng)的輸入數(shù)據(jù)x、y、m 來(lái)說(shuō),最大可以滿足4096 bit,能滿足現(xiàn)在對(duì)公鑰算法強(qiáng)度的要求。

當(dāng)要進(jìn)行計(jì)算時(shí),輸入x、y、m,即可通過(guò)此模塊計(jì)算得到結(jié)果C,即:C=x*ymodm,此為所要研究的大數(shù)模乘。

3.2 蒙哥馬利型大數(shù)模乘模塊內(nèi)部結(jié)構(gòu)設(shè)計(jì)

蒙哥馬利型大數(shù)模乘模塊的內(nèi)部結(jié)構(gòu)設(shè)計(jì)如圖3-2 所示:

圖3-2 蒙哥馬利型大數(shù)模乘模塊內(nèi)部結(jié)構(gòu)設(shè)計(jì)

本設(shè)計(jì)的運(yùn)算處理步驟是通過(guò)四次調(diào)用改進(jìn)的蒙哥馬利模乘算法,并且每次調(diào)用中輸入不同的數(shù)據(jù),最終得到?jīng)]有R-1影響的大數(shù)模乘。

在第一、二次調(diào)用中,將R2作為第二個(gè)乘數(shù)來(lái)進(jìn)行代入計(jì)算(在相同模數(shù)m 的情況下,R2的數(shù)值不變,可以重復(fù)使用),這一步得到X′=X*Rmodm與Y′=Y*Rmodm;第三次調(diào)用中將得到的X′、Y′作為操作數(shù)再進(jìn)行一次蒙哥馬利模乘計(jì)算,得到S′=X*Y*Rmodm; 第四次調(diào)用中,1 作為另一個(gè)操作數(shù)被代入計(jì)算,R 與R-1即可相互抵消,最終得到大數(shù)模乘運(yùn)算結(jié)果C=x*ymodm。

3.3 蒙哥馬利模乘單元模塊設(shè)計(jì)

如上文介紹,蒙哥馬利型大數(shù)模乘模塊實(shí)際上就是在不斷重復(fù)計(jì)算蒙哥馬利模乘算法的過(guò)程[14],所以設(shè)計(jì)大數(shù)模乘的關(guān)鍵就在于對(duì)于蒙哥馬利模乘單元模塊進(jìn)行設(shè)計(jì)實(shí)現(xiàn),也就是說(shuō)將章節(jié)2 中提到的改進(jìn)后的蒙哥馬利模乘算法MM(x,y) 設(shè)計(jì)為一個(gè)基本算法單元,目的是方便后續(xù)不斷調(diào)用,最終整體實(shí)現(xiàn)圖3-2 所示的蒙哥馬利型大數(shù)模乘模塊。

3.3.1 蒙哥馬利模乘單元介紹

如章節(jié)2 所介紹的改進(jìn)的蒙哥馬利模乘算法,計(jì)算兩個(gè)k bit 位數(shù)的蒙哥馬利模乘至少需要到k 個(gè)處理時(shí)鐘,通過(guò)觀察章節(jié)2 中MM(x,y) 算法流程里的步驟2,發(fā)現(xiàn)該算法的基本運(yùn)算過(guò)程是從低位到高位,逐bit 地處理數(shù)據(jù),即改進(jìn)算法采取的是全串行處理流程,一個(gè)時(shí)鐘僅進(jìn)行1 bit 的數(shù)據(jù)處理。

當(dāng)處理的數(shù)據(jù)位數(shù)較小時(shí),該算法是比較有效的,所耗時(shí)鐘周期也較少,然而對(duì)于現(xiàn)在的密碼算法來(lái)說(shuō),處理的都是位數(shù)較長(zhǎng)的數(shù)據(jù),例如RSA 應(yīng)用中就需要1024 bit 以上的大整數(shù)相乘,因此該算法在處理位數(shù)較長(zhǎng)的兩個(gè)數(shù)的模乘計(jì)算時(shí),計(jì)算速度會(huì)較慢。 本文通過(guò)設(shè)計(jì)使得該算法能夠在一個(gè)時(shí)鐘周期內(nèi)完成多位數(shù)的數(shù)據(jù)處理,即在同一個(gè)時(shí)鐘內(nèi)完成多次的乘法、加法以及移位處理,能夠有效地提高算法的效率。

3.3.2 蒙哥馬利模乘單元模塊設(shè)計(jì)

本設(shè)計(jì)中,難點(diǎn)集中在蒙哥馬利模乘運(yùn)算單元模塊中,完成對(duì)此部分的模塊化工作后,即完成了上文介紹的改進(jìn)蒙哥馬利模乘算法中的a=p+x(i)*y部分,在模乘實(shí)現(xiàn)的主程序中通過(guò)不斷循環(huán)調(diào)用此單元模塊,實(shí)現(xiàn)對(duì)數(shù)據(jù)的逐位計(jì)算處理,提升運(yùn)算處理效率。 圖3-3 展示了蒙哥馬利模乘算法單元的模塊化程序設(shè)計(jì)框圖。

圖3-3 mm_r2mm 模塊程序流程圖

本文將此程序記為“mm_r2mm”。 在模塊中,首先對(duì)于數(shù)據(jù)進(jìn)行初始化處理,將結(jié)果S、位標(biāo)志符i 賦0;再判斷乘數(shù)對(duì)應(yīng)的位是否為1,為1 則將輸入的乘數(shù)y 與S 相加處理,結(jié)果賦值給新S,否則S 值保持不變;再判斷S 的最低位是否為0,也就是對(duì)S 值進(jìn)行了一個(gè)奇偶判斷,若為0,則通過(guò)將S 值右移一位來(lái)實(shí)現(xiàn)除2 計(jì)算,不為0 則將S 值與模數(shù)m 值相加,所得值賦給新S 后再進(jìn)行右移一位操作,完成單次的數(shù)據(jù)處理,最后將結(jié)果S 的值返回,此即完成整個(gè)數(shù)據(jù)處理流程。

單個(gè)模塊單元在一個(gè)時(shí)鐘周期內(nèi)可以完成對(duì)于1 bit 數(shù)據(jù)的處理工作,圖3-4 展示了雙模塊設(shè)計(jì)方案,用以說(shuō)明在運(yùn)算過(guò)程中具體的調(diào)用方式,便于理解分析。

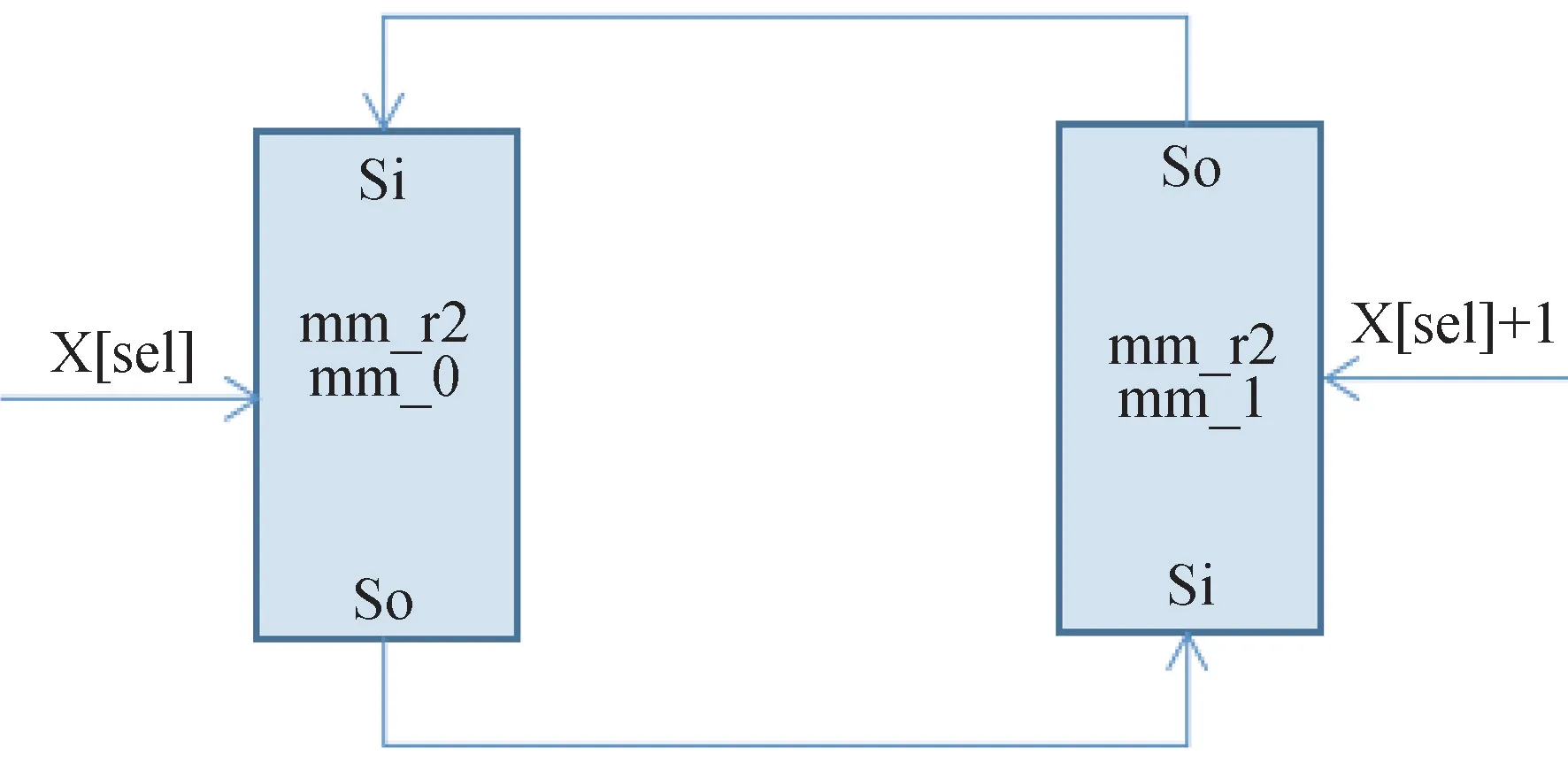
圖3-4 雙模塊數(shù)據(jù)處理流程

其中:x[sel]和x[sel]+1 分別為輸入數(shù)據(jù)x的對(duì)應(yīng)位。 雙模塊思想通過(guò)將模塊單元mm_r2mm_0 中的輸出數(shù)據(jù)So 作為模塊單元mm_r2mm_1 中的輸入數(shù)據(jù)Si,再將模塊單元mm_r2mm_1 中的輸出數(shù)據(jù)So 作為模塊單元mm_r2mm_0 的輸入數(shù)據(jù)Si。 這一操作實(shí)現(xiàn)了模塊單元間的數(shù)據(jù)連接傳遞,將運(yùn)算結(jié)果傳遞到下一次計(jì)算中,保證運(yùn)算處理的連續(xù)性,配合步進(jìn)信號(hào)對(duì)數(shù)據(jù)位進(jìn)行選擇控制,循環(huán)實(shí)現(xiàn)迭代運(yùn)算,直至處理到數(shù)據(jù)的最后一位。 表3-1 說(shuō)明了步進(jìn)控制信號(hào)在數(shù)據(jù)選擇時(shí)的作用,展示了具體的數(shù)據(jù)位處理過(guò)程。

表3-1 步進(jìn)信號(hào)Sel 與各處理位數(shù)的關(guān)系

3.4 蒙哥馬利模乘模塊總設(shè)計(jì)實(shí)現(xiàn)

本部分介紹改進(jìn)后的蒙哥馬利模乘算法,即MM(x,y) 的設(shè)計(jì)實(shí)現(xiàn)過(guò)程,以此實(shí)現(xiàn)蒙哥馬利模乘計(jì)算功能,具體流程如圖3-5 所示。

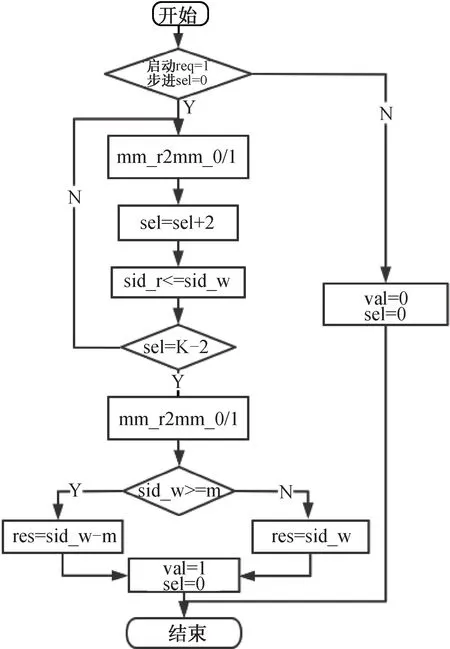
圖3-5 蒙哥馬利模乘模塊總程序框圖

表3-2 說(shuō)明了在程序框圖中出現(xiàn)各定義值及其在程序中的作用,方便對(duì)程序流程進(jìn)行解釋說(shuō)明。

表3-2 框圖中各信號(hào)定義及作用

配合表3-2 的說(shuō)明,對(duì)程序流程的介紹如下:

第一步對(duì)于程序的啟動(dòng)條件進(jìn)行判斷,當(dāng)req 啟動(dòng)信號(hào)值為1 且步進(jìn)選擇信號(hào)為0 時(shí)(數(shù)據(jù)可從最低位開(kāi)始處理),滿足啟動(dòng)條件,此時(shí)進(jìn)行3.3.2 章節(jié)中模塊程序的處理(mm_r2mm_0/1),進(jìn)行數(shù)據(jù)的迭代處理,同時(shí)將sel 步進(jìn)選擇信號(hào)進(jìn)行sel=sel+2 的處理,同時(shí)再將第1 個(gè)模塊單元mm_r2mm_0 的輸出值作為第2 個(gè)模塊單元mm_r2mm_1 的輸入數(shù)據(jù),實(shí)現(xiàn)單次數(shù)據(jù)處理的傳遞,再將mm_r2mm_1 的模塊輸出值sid_w 賦給mm_r2mm_0 的模塊輸入值sid_r,完成一次步進(jìn)中兩位數(shù)據(jù)處理結(jié)果的傳遞,傳遞進(jìn)行下一次步進(jìn)處理;

第二步進(jìn)行位數(shù)判斷處理,如果運(yùn)算到數(shù)據(jù)的最后兩位,即滿足這一判斷條件,就說(shuō)明了運(yùn)算處理已接近完成,此時(shí)再進(jìn)行最后一次模塊單元處理,完成后的迭代運(yùn)算結(jié)果也就是模塊單元mm_r2mm_1 的輸出值sid_w,若不滿足則返回到模塊程序,繼續(xù)進(jìn)行數(shù)據(jù)處理;

第三步進(jìn)行一次條件減法處理,如果模塊輸出值sid_w 大于等于模數(shù)m 的值,則將sid_w-m的值作為最終的運(yùn)算結(jié)果賦值給res,否則直接將作為運(yùn)算結(jié)果賦給res;最后將輸出結(jié)果標(biāo)志位val 置1,步進(jìn)選擇信號(hào)sel 置0,結(jié)束本次程序運(yùn)算。

本程序設(shè)計(jì)的主要運(yùn)算處理集中在對(duì)數(shù)據(jù)逐bit 位進(jìn)行迭代運(yùn)算的處理過(guò)程,也就是上文提到的“mm_r2mm_0/1”模塊程序,如果對(duì)于算法運(yùn)算處理效率不滿意,理論上是可以通過(guò)增加模塊單元的個(gè)數(shù),改變步進(jìn),使得在一個(gè)時(shí)鐘周期內(nèi)進(jìn)行多次數(shù)據(jù)處理,進(jìn)而減少總的迭代次數(shù),減少總的時(shí)鐘周期,進(jìn)而提升運(yùn)算效率。 從理論上分析,模塊的單元數(shù)量與運(yùn)算處理效率是成正比的,模塊單元數(shù)量越多,運(yùn)算處理效率越高,4 單元、8 單元、甚至16 單元都是可行的,但是過(guò)多引入模塊單元會(huì)引入更多的中間變量,在定義與調(diào)用時(shí)不利于整體程序的實(shí)現(xiàn),同時(shí)在實(shí)際應(yīng)用時(shí)會(huì)占用更多的存儲(chǔ)資源。 綜合考慮資源消耗與處理效率,本文設(shè)計(jì)將模塊的單元數(shù)量設(shè)置為2。

需要說(shuō)明的一點(diǎn)是,為了便于在功能仿真階段中通過(guò)時(shí)序圖來(lái)準(zhǔn)確對(duì)比出時(shí)鐘消耗數(shù),在本設(shè)計(jì)中引入的啟動(dòng)信號(hào)req 與輸出結(jié)果標(biāo)志信號(hào)val 也發(fā)揮了一定作用,通過(guò)觀察輸出波形中的指定返回信號(hào),即可快速統(tǒng)計(jì)出在功能仿真環(huán)節(jié)運(yùn)算消耗的總時(shí)鐘數(shù),關(guān)于這一內(nèi)容以及功能仿真所需要的相關(guān)文件的編寫設(shè)計(jì)將在下一章節(jié)作具體介紹說(shuō)明。

4 系統(tǒng)仿真

4.1 算法基本結(jié)構(gòu)的正確性驗(yàn)證

模乘運(yùn)算應(yīng)用最基本的形式為X*Ymodm,通過(guò)模乘算法的基本定理易知:如果將計(jì)算X 與Y 的值互換后,計(jì)算結(jié)果是不會(huì)改變的。借鑒這一想法,通過(guò)互換x、y 的值,觀察最終的運(yùn)算結(jié)果是否保持不變,在一定程度上也能夠說(shuō)明算法運(yùn)算結(jié)構(gòu)的正確性。 故本文在功能仿真環(huán)節(jié)將x 與y 值互換后進(jìn)行運(yùn)算仿真,仿真結(jié)果如下圖4-1、4-2 所示,結(jié)果未發(fā)生改變,說(shuō)明了算法結(jié)構(gòu)的正確性。

圖4-1 x、y 值未互換仿真結(jié)果

4.2 算法運(yùn)算結(jié)果的正確性驗(yàn)證

本文設(shè)計(jì)的蒙哥馬利型模乘法器能夠完成形如x*y*R-1modm的算法運(yùn)算,其中R 為常數(shù),取值為:R= 2k,與數(shù)據(jù)位數(shù)的選擇有關(guān)。

通過(guò)觀察其算法形式可以得出一個(gè)驗(yàn)證方法:如果將y 的取值確定為2k,那么算法的運(yùn)算形式就轉(zhuǎn)換為x*2k*2-kmodm,由于x 值小于模數(shù)m,則可知最終計(jì)算值為x。 在這一想法的基礎(chǔ)上,通過(guò)設(shè)定一組低位數(shù)據(jù)來(lái)進(jìn)行驗(yàn)證運(yùn)算,如果系統(tǒng)仿真運(yùn)算結(jié)果與理論分析一致,則系統(tǒng)運(yùn)算結(jié)果的正確性就得到了保障。

圖4-2 x、y 值互換后仿真結(jié)果

在這一步的驗(yàn)證中,設(shè)定x=10000000,m=11110001,對(duì)應(yīng)十六進(jìn)制數(shù)x=80,m=F1,本應(yīng)設(shè)置y=28=256,但由于本文設(shè)計(jì)中x、y、m應(yīng)滿足位數(shù)相同這一條件,故只能設(shè)置y=27=128,最終的運(yùn)算結(jié)果為:

通過(guò)Modelsim 軟件進(jìn)行測(cè)試,仿真測(cè)試結(jié)果如下圖4-3 所示,實(shí)際測(cè)試結(jié)果與理論分析值吻合,進(jìn)一步說(shuō)明了系統(tǒng)運(yùn)算的正確性。

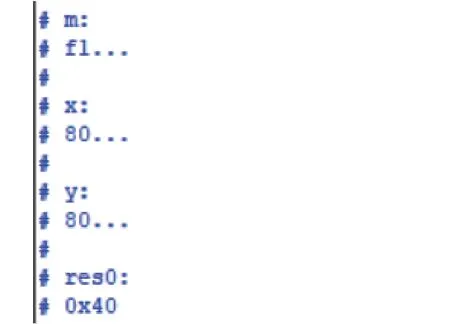
圖4-3 運(yùn)算正確性驗(yàn)證仿真測(cè)試圖

4.3 Modelsim 功能仿真分析

在上一部分中該算法模塊運(yùn)算正確性得以驗(yàn)證,確保該系統(tǒng)的計(jì)算功能在算法結(jié)構(gòu)上的正確無(wú)誤,但僅僅停留在對(duì)于小位數(shù)的計(jì)算處理中,因此在本部分中對(duì)于本文所設(shè)計(jì)的蒙哥馬利模乘器,在Modelsim SE 10.4 軟件中輸入測(cè)試多組數(shù)據(jù),展示計(jì)算處理功能的完備性。 首次輸入的測(cè)試數(shù)據(jù)類型為256bit 位二進(jìn)制數(shù),具體數(shù)值如下:

同時(shí)為了本系統(tǒng)的測(cè)試數(shù)據(jù)的完備性,以及展現(xiàn)系統(tǒng)在處理不同位數(shù)的大數(shù)模乘時(shí)運(yùn)算時(shí)間上的差異性,本文又在原來(lái)256 bit 位的基礎(chǔ)上,另行測(cè)試了以下三組數(shù)據(jù),分別從512 bit、1024 bit、4096 bit 不同位數(shù)展現(xiàn)本系統(tǒng)的仿真效果,配合啟動(dòng)信號(hào)req 以及輸出結(jié)果標(biāo)志信號(hào)val,即可得出具體的仿真運(yùn)算處理時(shí)間,此內(nèi)容由于在之前的部分中已經(jīng)進(jìn)行過(guò)展示,因此在本部分就不再贅述。 本部分主要展示所得的具體仿真結(jié)果,分別如圖4-5、圖4-6、圖4-7 所示。

圖4-4 256 位仿真測(cè)試結(jié)果

圖4-5 512 bit 仿真測(cè)試結(jié)果

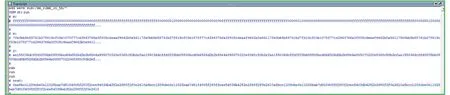
圖4-6 1024 bit 仿真測(cè)試結(jié)果

經(jīng)過(guò)設(shè)計(jì)測(cè)試,蒙哥馬利大數(shù)模乘計(jì)算系統(tǒng)理論上能夠計(jì)算的最大位數(shù)為4096 bit 二進(jìn)制數(shù),通過(guò)修改相關(guān)位寬K 參數(shù),即可完成限定位數(shù)內(nèi)任意位數(shù)的大數(shù)模乘運(yùn)算,在文本文件中修改輸入測(cè)試數(shù)據(jù)x、y 以及m 的具體數(shù)值,即可通過(guò)仿真任務(wù)窗口進(jìn)行相關(guān)計(jì)算數(shù)值的輸出展示。

5 總結(jié)

當(dāng)前各主流公鑰密碼算法如RSA,以及各類橢圓曲線加密算法都主要涉及到大數(shù)之間的運(yùn)算,尤其是模乘、模冪計(jì)算,而此類計(jì)算資源消耗大、運(yùn)算處理時(shí)間長(zhǎng),成為制約系統(tǒng)處理速度的瓶頸。

本文則以蒙哥馬利模乘算法為理論依據(jù),研究設(shè)計(jì)了大數(shù)模乘模塊,以Verilog 硬件描述語(yǔ)言編寫算法程序,并利用Modelsim 軟件進(jìn)行仿真功能測(cè)試,最后利用Altera 對(duì)此設(shè)計(jì)進(jìn)行綜合,完成研究。

與已有的大數(shù)模乘研究方案相比,本文設(shè)計(jì)具有以下優(yōu)點(diǎn):

1. 算法設(shè)計(jì)原理簡(jiǎn)單,設(shè)計(jì)結(jié)構(gòu)簡(jiǎn)介,易于硬件實(shí)現(xiàn);

2. 將串行改進(jìn)為并行運(yùn)算,利用模塊化思想使得數(shù)據(jù)處理效率得到較大提升,理論提升了二倍的處理速度;

3. 在功能仿真環(huán)節(jié),通過(guò)編寫測(cè)試文件的方式讀取輸入數(shù)據(jù),簡(jiǎn)化了數(shù)據(jù)輸入形式;

4. 數(shù)據(jù)處理位數(shù)區(qū)間充沛,可完成1 至4096 bit 范圍內(nèi)的蒙哥馬利模乘計(jì)算,并將運(yùn)算結(jié)果輸出反饋。

通過(guò)總結(jié)與比較,現(xiàn)階段本模塊還存在一些不足需要改進(jìn)完善,需要完成模冪運(yùn)算,以進(jìn)一步滿足RSA 等密碼算法的大數(shù)運(yùn)算要求。