SLIM 算法的9 輪不可能差分分析

鄭會超 魏錦鵬

北京電子科技學院,北京市 100070

引言

分組密碼是最成熟的密碼分支之一,具有速度快、易于標準化和便于軟硬件實現等特點,是一種非常重要的加密方案。 分組密碼作為信息與網絡安全中實現數據加密、消息鑒別及密鑰管理的核心密碼算法,在計算機通信和信息系統安全領域有著廣泛的應用。 近年來,隨著物聯網的發展,無線傳感器網絡(WSN)和無線射頻技術(RFID)的應用越來越廣泛,它們具有硬件制造、維護成本低,網絡健壯性、自組織性強,適用性廣泛的特點,已成為物聯網應用的關鍵組成部分。WSN 和RFID 基于無線網絡傳輸信息,攻擊者更加容易獲得、干擾甚至破壞信息傳輸。 由于物聯網上使用的微型計算設備計算能力有限,人們開始越來越關注輕量級分組密碼算法的研究來保證信息的安全[1]。 輕量級分組密碼算法作為一種特殊的分組密碼算法,它們在硬件實現、加密速度、運行功耗等方面與AES 等傳統分密碼相比有明顯的優勢,更適合物聯網微型計算設備使用。 在這種情況下,大量輕量級分組密碼算法被研究出來,其中比較典型的有Lblock[2],LED[3],PRESENT[4], SIMON[5], Midori[6], SKINNY[7],HIGHT[8],SIMECK[9]等。

一個密碼算法能夠被廣泛應用不僅應具有較高的實現效率,更重要的是保證算法的安全性。 然而,密碼設計者在設計密碼算法過程中,有時會追求高效性導致安全性降低,因此,采用多種密碼分析方法去分析算法的安全性是很有必要的。 目前輕量級分組密碼分析方法主要包括線性分析[10]、差分分析[11]、 截斷差 分分析[12]、不可能差分分析[13]、積分分析[14]、相關密鑰分析[15]、Biclique 分析[16]等。

2020 年,Aboushosha 等人提出了一個新的輕量級分組密碼SLIM[17]。 Aboushosha 等人表明,SLIM 算法能有效抵抗差分分析和線性分析,并給出了7 輪差分路徑和11 輪線性路徑。 目前還沒有文獻對SLIM 算法進行不可能差分分析,本文試圖對SLIM 算法進行不可能差分分析,以進一步評估其安全性。 本文充分利用了SLIM算法輪函數的具體細節,特別是挖掘非線性組件S 盒的差分性質,并結合P 置換設計,利用差分方程求解的方法構造出SLIM 算法的6 輪不可能差分區分器。 進一步,本文利用構造的區分器攻擊了9 輪SLIM 算法,攻擊的數據復雜度為229個選擇明文,時間復雜度為255.83次9 輪加密。

1 SLIM 算法簡介

1.1 SLIM 算法的整體框架

SLIM 算法整體采用Feistel 結構,輪函數采用類似于PRESENT 算法的SP 結構,其中S 盒為4 比特,P 置換采用16 比特的比特拉線設計。SLIM 算法的分組長度為32 比特,密鑰長度為80比特,算法總輪數為32 輪。 該算法的整體加密流程如圖1 所示。

圖1 SLIM 算法的加密流程

在加密時,將32 比特的分組數據分為左右各16 比特,即左支Li和右支Ri均為16 比特。若一輪迭代的輸入為(Li,Ri), 輸出為(Li+1,Ri+1),則有:Li+1=Ri;Ri+1=Li⊕F(Ri,Ki),其中,Ki表示第i 輪的輪密鑰,F 表示輪函數。

1.2 SLIM 算法的輪函數

SLIM 算法輪函數F 的加密流程由輪密鑰加、S 層和P 置換3 部分組成,如圖2 所示。

圖2 SLIM 算法輪函數F 的加密流程

輪密鑰加:分組加密數據的右支Ri與第i輪的輪密鑰Ki進行逐比特異或。

S 層:由4 個相同的4 比特S 盒并行加密,SLIM 算法中的 4 比特 S 盒與國際標準PRESENT 算法的S 盒相同,如表1 所列。

表1 SLIM 算法的S 盒

P 置換:按照比特拉線設計,即16 比特數據按照表2 的規律進行比特置換。 在表2 中,輸入的第i 比特經過P 置換后變為第P(i)比特。

表2 SLIM 算法的P 置換

在研究不可能差分區分器的構造時,由于輪密鑰不影響差分的傳播,因此本文不詳細介紹SLIM 的密鑰擴展算法,具體細節見文獻[17]。

2 SLIM 算法的6 輪不可能差分區分器

構造盡可能長的不可能差分區分器是不可能差分分析的核心。 本節首先挖掘SLIM 算法S盒的具體細節,給出一個關于S 盒的差分性質;然后利用該性質,結合P 置換的加密流程,構造出SLIM 算法的一條6 輪不可能差分區分器。根據表1 給出的SLIM 算法的S 盒,利用python編程搜索S 盒的差分分布表,如表3 所示。

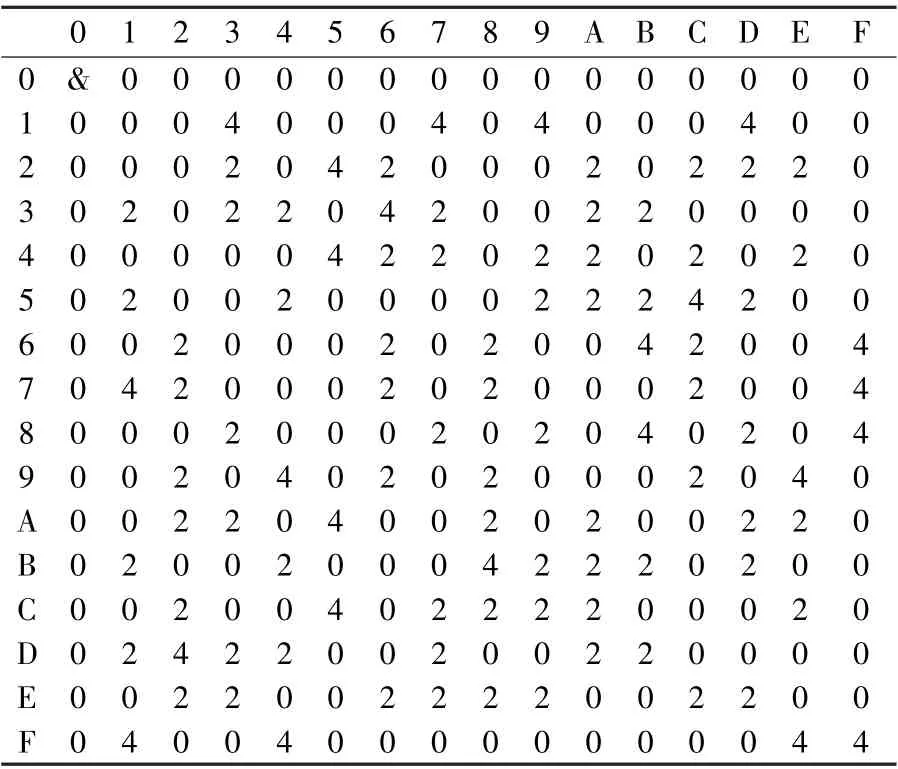
表3 SLIM 算法S 盒的差分分布表

在表3 中,第1 列為S 盒的輸入差分,第1行為S 盒的輸出差分,輸入與輸出差分均用16進制表示,中間的值為該輸入輸出差分方程對應的解的個數。 例如,當S 盒的輸入差分為0x2時,輸出差分為0x3 時,滿足該差分方程的解的個數為2。 注意當解的個數為0 時,說明該輸入差分和輸出差分不匹配,即該輸入差分經過S 盒后不能傳播到該輸出差分。

通過觀察SLIM 算法S 盒的差分分布表,容易得到如下性質。

性質1 對于SLIM 算法的S 盒,當輸入差分分別為0x1,0x8,0x9 時,經過S 盒后輸出差分分別為***1,***1 和***0,以概率1 成立。其中*表示該比特差分可能為0 也可能為1。

證明 以0x8→***1 為例進行分析。 根據表3,當輸入差分為0x8 時,輸出差分可能為0x3,0x7,0x9,0xB,0xD,0xF,則輸出差分前3 比特0 或1 均能夠出現,但是最低比特差分一定為1,即輸出差分的形式為***1。 因此,0x8→***1 以概率1 成立。 類似地,可以說明0x1→***1和0x9→***0 以概率1 成立。

下面利用性質1 并結合P 置換的特點,給出定理1。

定理1 在SLIM 算法中,當輸入差分為(X,016),輸出差分為(016,Y) 時, (X,016) →(016,Y) 是SLIM 算法的一條6 輪不可能差分區分器,如圖3 所示。 其中X 滿足(*12| 1000),Y 滿足(012| 1000),*i表示連續i 個*,0i表示連續i 個0。 “｜”表示比特串之間的連接。

證明 首先從正向加密開始計算,正向輸入差分為(X,016), 經過1 輪加密后輸出差分為(016,X), 經過2 輪加密后輸出差分為(X,F(X)),經過3 輪加密后輸出差分的左分支為F(X),計算結果如表4 所示。

表4 輸入差分X 的加密

然后從逆向進行運算,逆向的輸出差分為(016,Y),由于SLIM 算法結構為Feistel 型,加解密運算是相同的,所以逆向解密運算的輪函數與正向加密的輪函數相同。 輸出差分經過1 輪解密后,輸出差分仍為(016,Y),經過2 輪解密后輸出差分為(Y,F(Y)),經過3 輪解密后輸出差分右分支為F2(Y) ⊕Y。 計算結果如表5 所示。

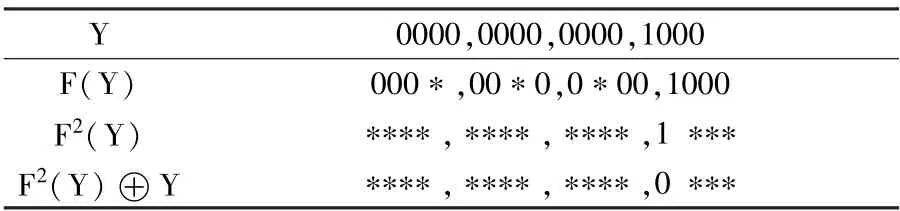
表5 輸出差分Y 的解密

由圖3 可知,需要對比正向加密3 輪的輸出差分左分支與逆向解密3 輪的輸出差分的右分支,即需要對比F(X) 與F2(Y) ⊕Y 的值,由表4 和表5 容易看出二者之間存在矛盾,故(X,016) →(016,Y) 是SLIM 算法的一條6 輪不可能差分區分器,定理1 成立。

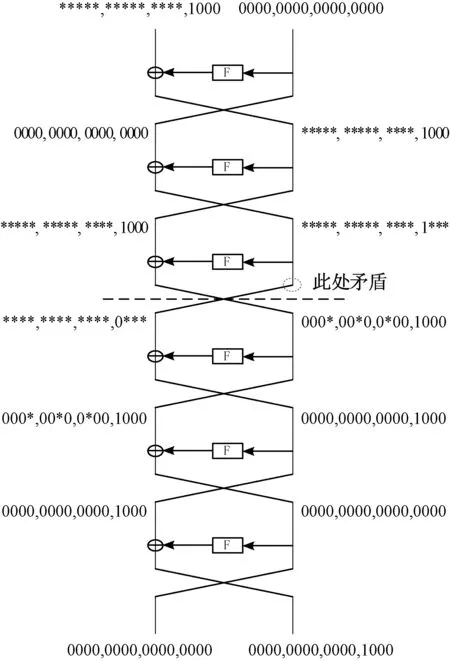
圖3 SLIM 算法6 輪不可能差分區分器

3 SLIM 算法的9 輪密鑰恢復攻擊

本節在上節構造的6 輪不可能差分區分器的基礎上,添加1 輪前置路徑和2 輪后置路徑,對SLIM 算法進行9 輪不可能差分攻擊。 圖4 為攻擊9 輪SLIM 算法的示意圖。

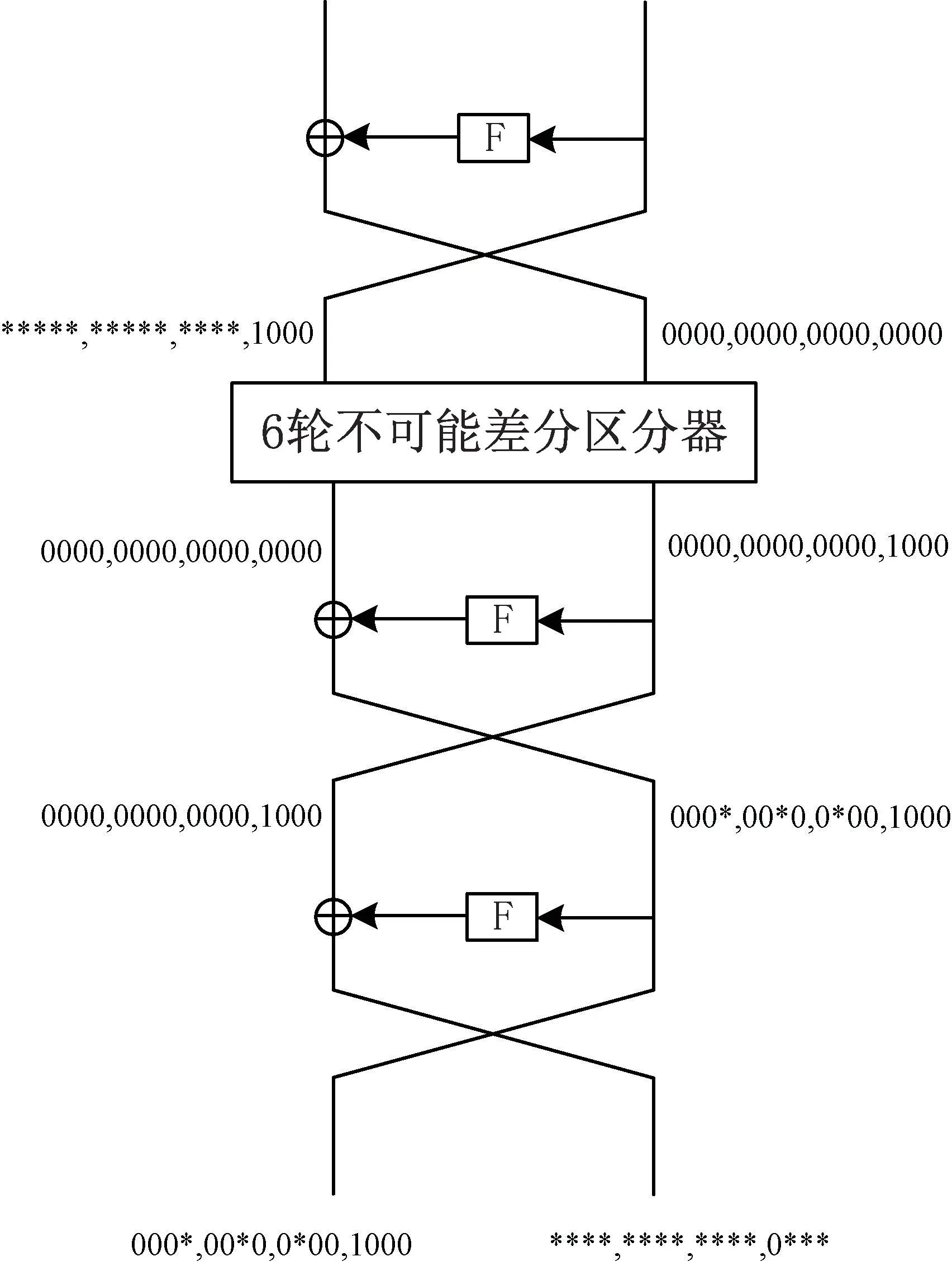
圖4 SLIM 算法9 輪不可能差分攻擊

步驟1 選取一個結構,在該結構內任意選擇兩個明文進行異或,它們的差分需要滿足如下形 式: (****, ****, ****, 1***, ****,****,****,1000)。 該結構能夠提供227個明文和253組明文對。

步驟2 選擇2n個上述結構,則這些結構總共能提供2n+27個明文和2n+53組明文對。 選擇密文差分滿足以下形式的密文對留下:(000*,00*0,0*00,1000,****,****,****,0***),保留下來的明密文對數目約為2n+53× 2-14=2n+39。

步驟3 對于保留下來的明密文對,猜測最后一輪的輪密鑰K9的全部16 比特密鑰,即～,使得關于4 個S 盒的差分方程都成立。在平均意義下,每4 個比特通過S 盒使差分方程成立的概率約為2-4,則4 個差分方程同時成立的概率為2-4×4。 因此,經過步驟3 后剩余明密文對的數目約為2n+39× 2-16= 2n+23。

步驟4 對于剩余的明密文對,猜測第8 輪的輪密鑰K8的低4 比特密鑰,即～,使得關于最右邊S 盒的差分方程成立,差分方程成立的概率約為2-4。 因此,經過步驟4 后剩余明密文對的數目約為2n+23× 2-4= 2n+19。

步驟5 對于經過上述步驟處理的剩余明密文對,猜測第1 輪的輪密鑰K1的全部16 比特密鑰,即～,若關于4 個S 盒的差分方程都成立,則篩除步驟3 到步驟5 中猜測的36 比特密鑰。

當猜測的36 比特候選密鑰滿足不可能差分的輸入輸出時,猜測的密鑰一定是錯誤的,密鑰是錯誤的概率是2-16。 經過2n+19組明密文對的篩選,最終剩余錯誤密鑰的個數N=(236- 1)×(1- 2-16)2n+19。 為使N?1,本文取n=2,此時錯誤密鑰都被淘汰,剩下的即為正確密鑰。

復雜度分析:在上述攻擊中,當n=2 時,數據復雜度為229個選擇明文。 時間復雜度主要由步驟3 到步驟5 提供。 在步驟3 中,解密過程涉及4 個S 盒,而1 輪解密共涉及4 個S 盒,因此步驟3 的時間復雜度為2× 241× 216× 4/4=258次1 輪解密;在步驟4 中,解密過程只涉及1 個S 盒,因此步驟4 的時間復雜度為2× 225× 216×24× 1/4= 244次1 輪解密;在步驟5 中,加密過程涉及4 個S 盒,而1 輪加密共涉及4 個S 盒,因此步驟5 的時間復雜度為2× 221× 216× 24×216× 4/4= 258次1 輪加密。 故總的時間復雜度為258+ 244+ 258≈259次1 輪加密,即259÷ 9 ≈255.83次9 輪SLIM 算法加密。

4 結束語

本文主要研究了SLIM 算法在抵抗不可能差分攻擊時的安全性問題。 通過仔細研究輪函數的結構,本文構造了SLIM 算法6 輪不可能差分區分器,并利用該區分器攻擊了9 輪SLIM 算法。 通過上述攻擊可以恢復K1的16 比特密鑰,K8的4 比特密鑰和K9的16 比特密鑰,共計36比特密鑰信息,該攻擊的數據復雜度為229個選擇明文,時間復雜度為255.83次9 輪加密。 本文研究表明SLIM 算法在抵抗不可能差分攻擊時有足夠的安全冗余。 SLIM 算法是否存在更長的不可能差分區分器是我們下一步的研究工作。