橋梁結構監測數據異常值處理方法

岳加利，郝 靜，盧海林，余 勇，孫舒暢，李培軒

武漢工程大學土木工程與建筑學院，湖北 武漢430074

橋梁結構健康監測領域的研究與應用已發展了近30年，近年來愈發受到國內外學者的廣泛關注［1］。而橋梁健康監測系統每天都會采集海量監測數據，這些監測數據往往存在很多噪聲信息和異常值，甚至會因為各種干擾導致數據失效［2-4］。若使用帶干擾的監測數據直接進行后續研究，將會降低結論的可靠性和準確性，不利于橋梁健康狀態的準確評估與安全預警［5］。因此，亟需對海量監測數據進行處理與分析。

顏飛等［6］提出一種橋梁建筑質量運營監測數據處理方法，運用Hadoop平臺執行清洗監測數據、剔除無關數據和補齊缺失數據；Fu等［7］提出一種非常有效的故障數據恢復“三步走”策略，使用估計值或采用校正函數處理值（如均值處理、平滑趨勢項處理等）替換了故障數據；韓曉健等［8］采用改進的數據跳躍法剔除某疊合梁橋健康監測數據的粗差，解決了監測數據中多級異常跳躍的問題；吳運宏等［9］針對橋梁健康監測系統中的數據異常問題，提出基于微簇的數據流異常檢測框架，該方法在湖北某大橋的數據檢測上表現出了較好的異常識別能力；Yi等［10］闡述了異常監測數據的數據特征及其表現形式，并給出異常數據產生的部分原因；涂成楓等［11］利用應變閾值和小波細節系數進行異常信號識別，并通過多尺度關聯性分析對各頻率組分下的橋梁應變進行分類，確定了溫度對應變的影響；Moyo等［12］基于小波變換對大跨度橋梁應變數據進行分析，利用小波系數時間序列的變化識別了監測數據中的異常信號。

綜合相關研究發現：一方面，國內外已有研究對海量橋梁監測數據的有效性關注較少，處理異常數據時缺少對數據分布形式的考量；另一方面，大多主觀割裂了監測過程和處理過程，分析數據時采用的方法依賴于復雜的領域知識，不利于實際的工程應用。針對以上問題，本文基于灰色關聯度評估海量監測數據的有效性，采用改進箱型圖剔除和補全異常數據，對溫度和應變進行相關性分析，并基于Spearman相關系數驗證了改進箱型圖的可靠性和優越性。

1 數據處理原理

1.1 基于灰色關聯度的有效性評估

判斷監測數據的有效性是橋梁健康監測的首要工作，一旦數據出現問題將會給后續的監測、預警和評估工作帶來很大的困擾［13］。同截面同類型傳感器的正常數據序列應具有一定的關聯性，本文采用MATLAB分析同截面同類型傳感器獲得的數據序列，基于灰色關聯度對海量監測數據進行有效性評估。

采用灰色關聯度方法定量描述橋梁監測數據各參數的相互關系或變化趨勢，工作量小、易于掌握，且能夠較簡便地判斷海量監測數據的有效性［14-15］。具體步驟如下：

1.2 基于改進箱型圖的異常值剔除與補全

箱型圖是利用數據的最大值、最小值、中位數、上四分位數與下四分位數來描述數據的一種方法，對數據的分布形式無要求。應用拉格朗日插值法對箱型圖改進后能夠直接替換異常值，既簡化了處理過程又能夠得到客觀準確的結果。箱型圖各部分如圖1所示。

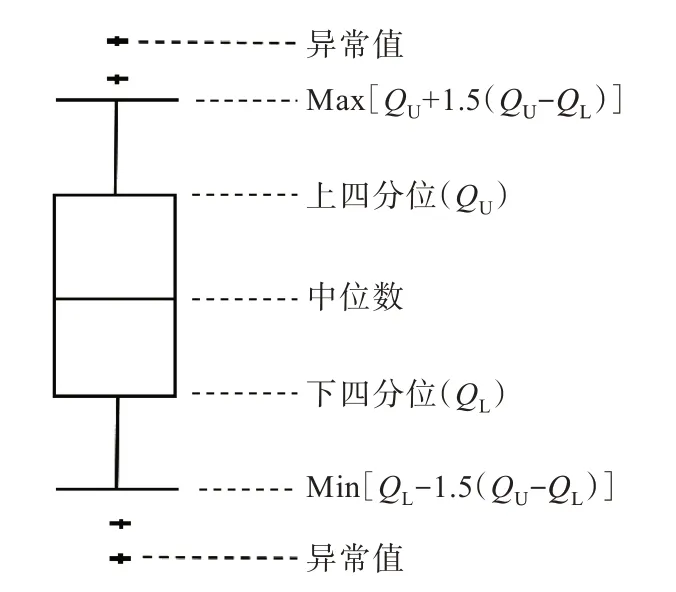
圖1 箱型圖示意Fig.1 Schematic of box plot

拉格朗日插值法通過使用多項式函數近似輸入與輸出之間的關系。對于n+1個樣本點（x0，y0），···，（xi，yi），···，（xn，yn），在［a，b］內給定任意x，可計算出x處對應的估計值，其公式如下：

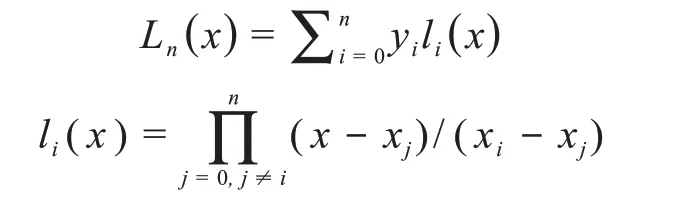
式中，Ln（x）為拉格朗日插值多項式，i是n+1個數，yi是xi處的函數值，xi、xj為互異節點，li（x）為基函數。

改進的箱型圖進行異常值處理的主要步驟為：步驟1，求解數據的上分位數QU、下分位數QL與中位 數；步 驟2，設定Max=QU+1.5（QU-QL）、Min=QL-1.5（QU-QL）；步驟3，如果滿足date＞Max或者date＜Min則判定為異常值；步驟4，刪除異常值，并采用拉格朗日插值法補全因此產生的空缺值；步驟5，重復步驟1～步驟4，檢驗異常值處理情況。

2 工程背景

武漢市某三跨（49 m+72 m+42 m）預應力混凝土變截面連續梁橋，上部結構為單箱單室箱梁，頂板寬12.49 m，懸臂長2.5 m，頂板懸臂端部厚22 cm，懸臂根部厚60 cm。如圖2所示，已在主橋中跨和邊跨的1/2截面處安裝了應變傳感器和溫度傳感器。應變傳感器為振弦應變計，共2個（S1和S2）分別安裝在箱梁內部底板的左右兩側；溫度傳感器為數字溫度計，共15個，T1安裝在鋪裝層內，T2～T6安裝在翼緣根部的混凝土內，T7安裝在翼緣板下部，T8～T11貫穿腹板，T12～T15安裝在底板上。應變測點截面和溫度測點截面數據相同，傳感器布置如圖3所示。

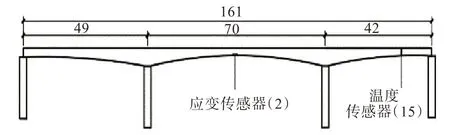
圖2 梁橋立面圖（單位：m）Fig.2 Elevation of beam bridge（unit：m）

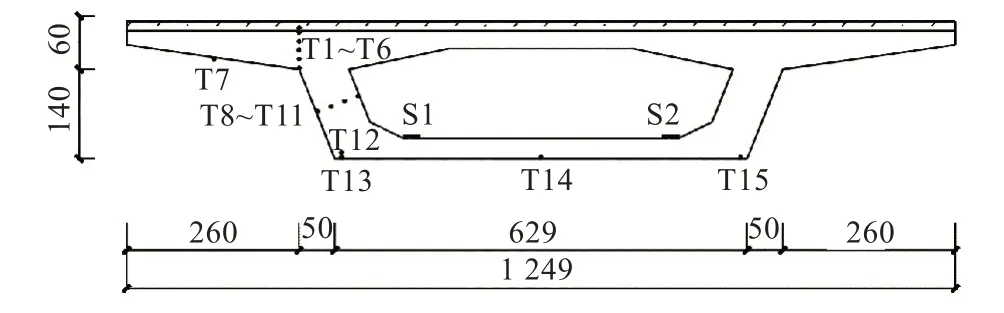
圖3 傳感器布置圖（單位：cm）Fig.3 Diagram of sensor layout（unit：cm）

3 數據處理分析

3.1 有效性評估

分別選取為期30 d（2020-12-27-2021-01-25）的應變數據與溫度數據進行關聯度分析。應變數據共有2組，以其中一組數據為參考序列，另一組數據為比較序列，算得r1-2=0.932 3，位于0.9～1的區間內。溫度數據共有15組，以第一組數據為參考序列，其余14組數據均為比較序列，求得灰色關聯度如表1所示。

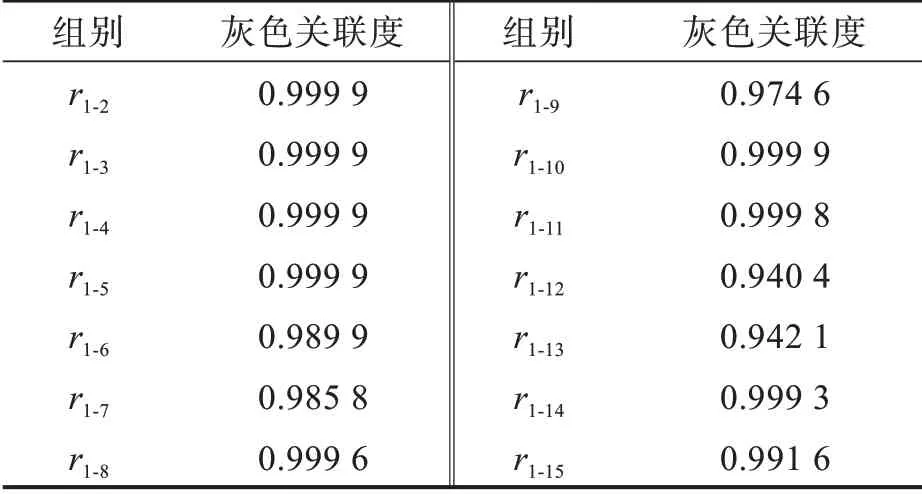
表1 溫度灰色關聯度Tab.1 Temperaturegrey correlation

從表1可知，14組溫度比較序列與參考序列所計算的灰色關聯度位于0.9～1的區間內。分別從應變數據和溫度數據中選擇50組數據作為樣本數據，根據文獻［16］中的閾值公式rij-2 ||σij計算有效性閾值。經檢驗，靜應變數據和溫度數據均滿足有效性要求。

3.2 異常值剔除和補全

采用箱型圖對通過有效性評估的溫度數據與應變數據進行異常值檢測，并采用改進后的箱型圖進行異常值剔除和補全。如圖4和圖5所示，溫度數據表現正常，而應變數據存在異常值。應變數據經過改進箱型圖處理后得到圖6，可以看出應變數據趨于平穩，處理效果較好，有利于后續橋梁狀態評估與安全預警。

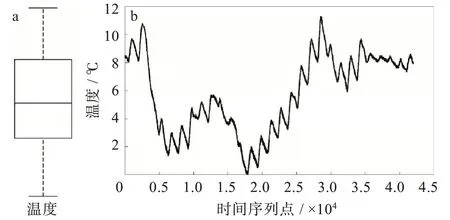
圖4 溫度數據分析：（a）異常值檢測，（b）監測曲線Fig.4 Temperature data analysis：（a）outlier detection，（b）monitoring curve

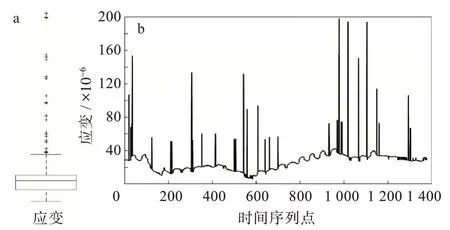
圖5 原始應變數據分析：（a）異常值檢測，（b）監測曲線Fig.5 Raw strain data analysis：（a）outlier detection，（b）monitoring curve

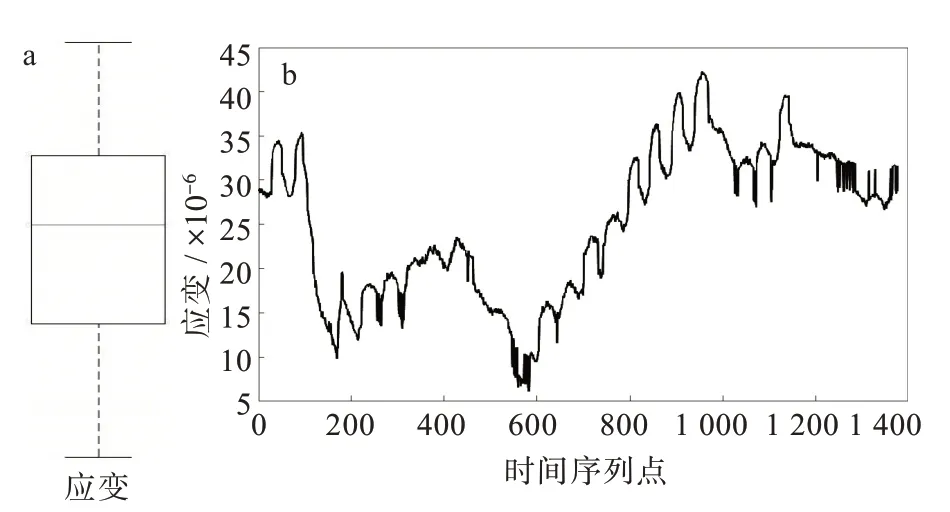
圖6 改進箱型圖處理后的應變數據分析：（a）異常值檢測，（b）監測曲線Fig.6 Analysis of strain data processed by improved box plot：（a）outlier detection，（b）monitoring curve

3.3 相關性分析

在橋梁實際運營中，溫度是影響應變的主要因素之一，文獻［17-18］通過分析溫度和應變數據發現溫度和應變呈較強的相關性。為了消除不同量綱和量綱單位給溫度和應變分析過程帶來的不利影響，按照公式（xmax為監測數據最大值，xmin為監測數據最小值，μ為監測數據均值，σ為監測數據標準差）對數據進行歸一化和標準化處理［19］。處理后的溫度與應變趨勢圖如圖7所示。

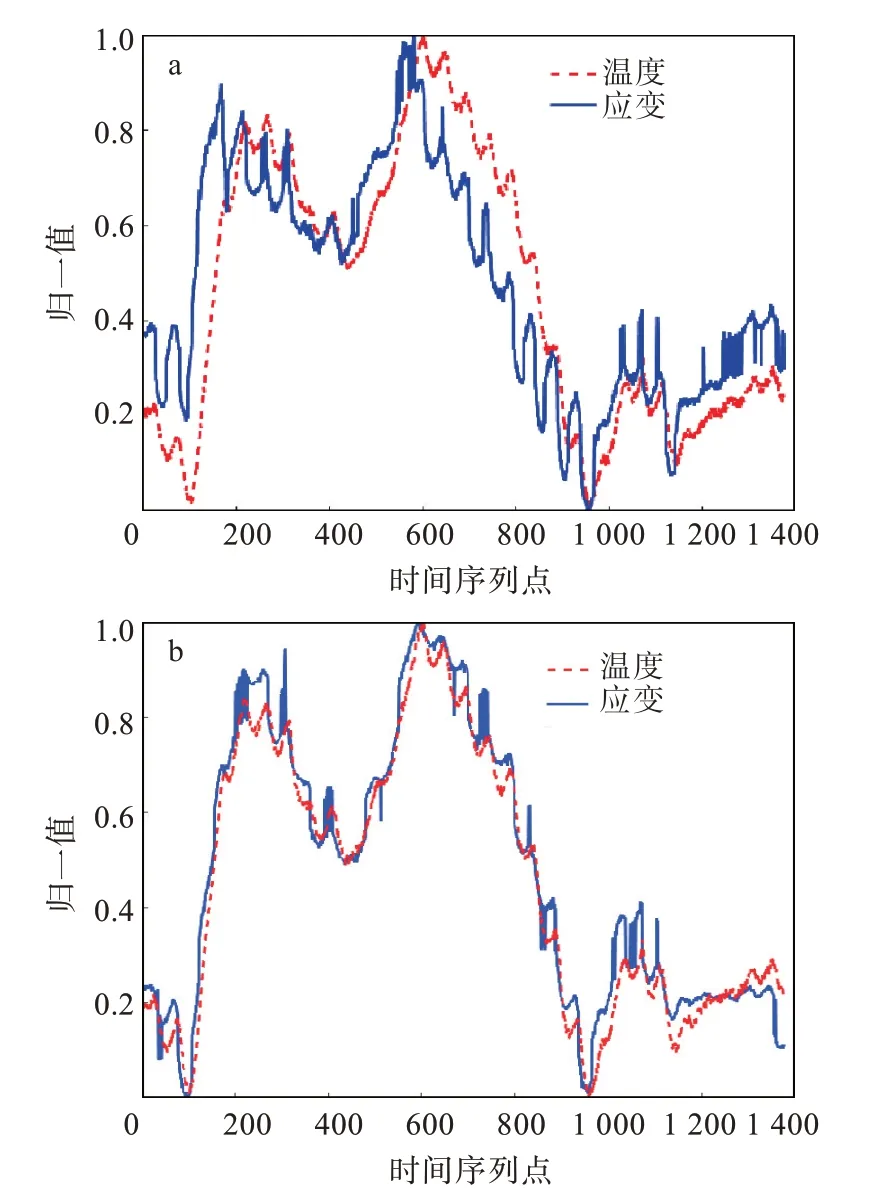
圖7 溫度與應變相關性分析：（a）S1處，（b）S2處Fig.7 Correlation analysis of temperature and strain：（a）S1，（b）S2

可以發現，經過歸一化和標準化處理的溫度數據和應變數據的數值都處于［0，1］之間，兩者曲線的變化趨勢一致，說明溫度數據和應變數據的相關性較強。

3.4 對比驗證

Spearman相關系數通常也稱為斯皮爾曼秩相關系數，它根據原始數據的排序位置估計2個變量之間的關聯程度與方向，對樣本的分布形式與容量大小無嚴格要求，適用于橋梁健康監測數據分析［20］。

假設2個隨機變量分別為X、Y，它們的元素個數均為n，2個隨機變量的第i（1≤i≤n）個值分別用Xi、Yi表示。對X、Y進行排序，得到2個元素集合x、y，其中元素xi、yi分別為Xi在X中的排行以及Yi在Y中的排行。Spearman相關系數根據公式rs=1-計算。

分別求得基于原始數據、拉依達準則處理的數據和改進箱型圖處理的數據中S1處和S2處的溫度和應變之間的Spearman相關系數，如表2所示。其中，基于拉依達準則處理后的數據與原始數據的相關系數相差不大，而基于改進箱型圖處理后的數據相關系數明顯提高，表明使用該方法去除異常數據能取得較好效果。

表2 溫度和應變的Spearman相關系數Tab.2 Spearman correlation coefficients of temperature and strain

4 結 論

本文以武漢市某混凝土連續梁橋健康監測系統為依托，對海量監測數據進行處理和分析，得到以下結論：

（1）基于灰色關聯度方法對海量監測數據進行有效性評估：同截面的2組應變數據的關聯度為0.932 3，同截面的15組溫度數據的關聯度位于0.9～1的區間內，并且均通過有效性檢驗，說明應變數據和溫度數據有效。

（2）經過改進箱型圖處理后，溫度和應變數據都獲得了較好的平穩性。采用改進的箱型圖不僅可檢測出異常數據，而且能將其直接剔除與補全，既簡化了處理過程又能夠得到相對準確的結果。

（3）分析歸一化和標準化處理后的溫度與應變數據，發現溫度和應變的相關性較高。進而，分別求出基于原始數據、拉依達準則處理后的數據和改進箱型圖處理后的數據中兩組溫度和應變之間的Spearman相關系數，結果表明采用改進箱型圖對異常數據進行剔除與補全具有較好效果。