非簡諧振動對石墨烯量子電容和熱穩定性的影響

吳 強，高君華，2，周虹君，鄭瑞倫

(1.重慶文理學院重慶市高校新型儲能器件及應用工程研究中心，重慶 402160;2.黑龍江大學 電子工程學院，哈爾濱 150080)

1 引 言

自1987 年Luryi 提出量子電容的概念和2008年石墨烯制備成功以來［1］，人們已對石墨烯材料的量子電容進行了不少研究.John 等人［2］對二維電子氣的量子電容進行了計算，Fang 等人［3］對單層石墨烯、Guo 等人［4］對石墨烯納米帶、Kliros［5］，Cheremisn［6］，Alisultanov 等人［7］對雙層石墨烯、Trabelsi［8］對在SiC 上的外延石墨烯分別與對應材料的量子電容進行了研究.Bhahcharya 等人［9］還對具有曲折邊界的單層和石墨烯納米帶的量子電容進行估計，Xia 等人［10］對如何精確測量量子電容問題開展實驗研究.2015 年楊光敏等［11］使用密度泛函理論的第一性原理，采用VASP 軟件包，在廣義梯度近似下，對N 摻雜石墨烯的量子電容進行研究并分析量子電容提升儲能的原因.但這些研究未反映出溫度等對量子電容的影響，更未研究量子電容的熱穩定性問題.2020 年Davydov［12］對石墨烯納米結構的量子電容從模型上給以予測，得到石墨烯納米結構量子電容變化規律的解析式.該文雖提到量子電容隨溫度變化，但研究中認為原子靜止，未考慮到原子的非簡諧振動，體現不出原子相互作用對量子電容的影響，而且也未研究它的熱穩定性問題.

石墨烯材料具有完美的晶體結構和獨特的電學、光學、熱學、力學等性能，在電子器件、能量儲存、環境科學等領域具有廣泛的應用前景.它的突出應用之一是制作超級電容器.在實際應用中，多變的外場以及多變的高溫環境，原子非簡諧振動效應突出，不僅使石墨烯材料的性質隨溫度發生變化，而且使材料發生形變，影響材料的性能穩定性和超級電容器的使用壽命.考慮到原子振動非簡諧效應，確定石墨烯材料量子電容隨溫度、外電場等的變化規律及其熱穩定性，這對于石墨烯材料在超級電容器等儲能器件上的應用就是一個亟待解決的重要問題.為此，本文將應用固體物理理論和方法，對此問題進行研究，以期對提高超級電容器儲能性能問題提供理論參考.

2 物理模型

我們研究的石墨烯是由N 個碳原子構成的二維六角格子平面系統，設平面為OXY 平面，Z 軸垂直向上，坐標系選取如圖1 所示.一個原子的平均原子相互作用能為［13］:

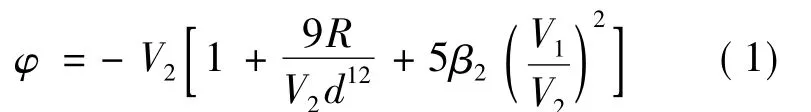
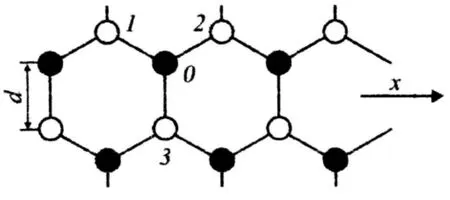
圖1 石墨烯的結構示意圖Fig.1 Schematic diagram of the structure of graphene

其中，V2為兩原子的sp2軌道σ 鍵的共價能，它與原子間距離d 的平方成反比:這里的m 為自由電子的質量; V1為金屬化能，R=0.154 ×104( ?2/2m)，a0為玻爾半徑，β2是與維數有關的參量，β2=2/3.

原子在平衡位置附近作非簡諧振動，將原子相互作用能φ( d) 在平衡位置d0附近展開，偏離δ=d - d0很小時，有

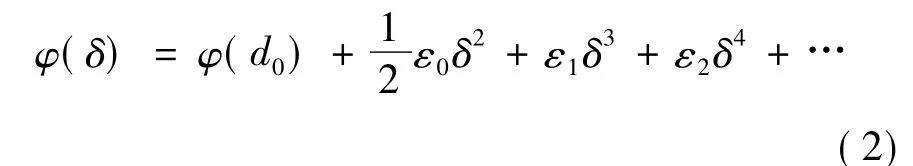
其中，ε0、ε1、ε2分別是簡諧系數、第一和第二非簡諧系數.其具體表示式見文獻［14］所述.

3 石墨烯量子電容隨溫度和電壓的變化

John 等人［2］給出電荷密度與電子態密度的關系為:

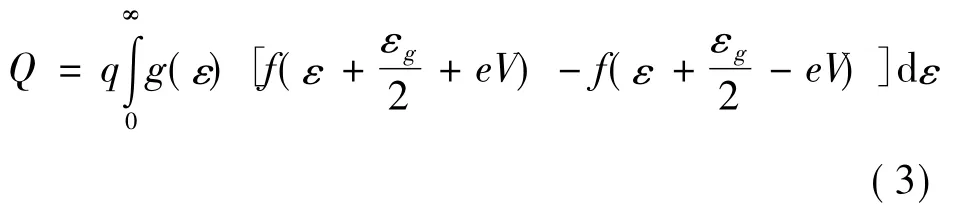
其中，g( ε) 為電子的態密度，它與一個原子上的平均態密度ρ( ε) 的關系為ρ( ε)=g( ε) /N，f( ε) 為費米分布函數，εg為禁帶寬度.將( 3) 式代入量子電容CQ的定義式，即單位質量( 或單位面積) 材料因量子效應產生電荷量改變dQ 對電勢差dV 的比值:

對單層石墨烯，禁帶寬度εg=0 ，求得石墨烯量子電容隨溫度和電壓的變化為［15］:

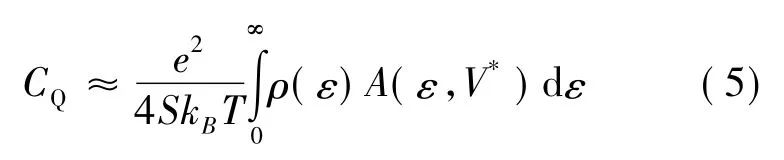
這里，

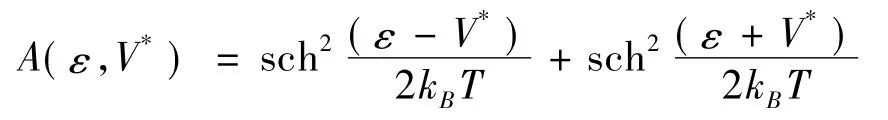
而ρ( ε) 為一個原子上的平均態密度，V*=eV，V是外電場電勢; S 是一個表面原子所占面積，對于石墨烯，為晶格常數.按照文獻［13］，單層石墨烯的態密度為:

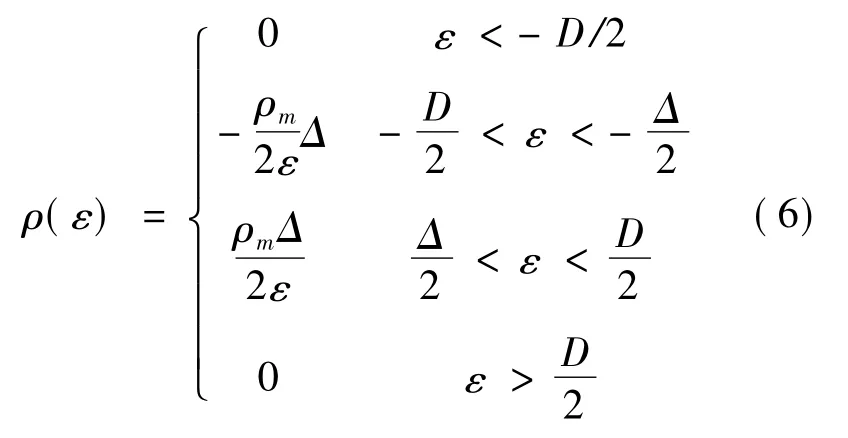
將(6) 式代入(5) 式，并令τ=t/2kBT，ν*=eV/2kBT，得到不考慮原子非簡諧振動時的量子電容為［15］:

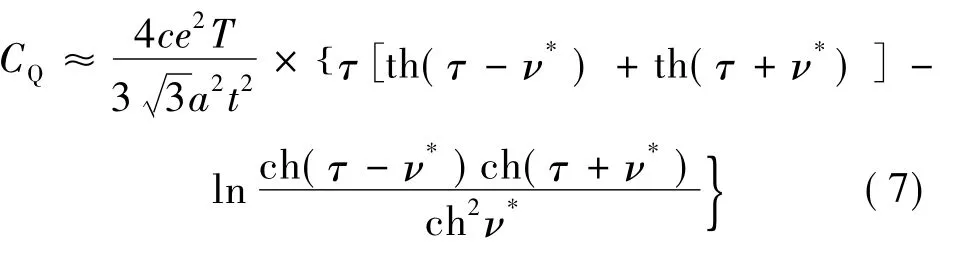
其中，c=2/(1 +2ln3) ，而t 是最近鄰格點的交換能.

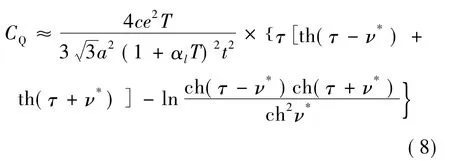
其中，線膨帳系數為［16］:

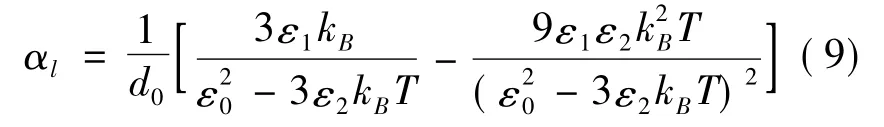
這里的d0為絕對零度時最近鄰原子間的距離.

4 石墨烯量子電容的熱穩定性隨溫度的變化

材料在熱、電、光、化學等內外因素作用下，性能逐漸降低，甚至完全喪失使用價值，這種現象叫材料的老化( Ageing).除材料老化以及材料摻雜、缺陷等會影響石墨烯蓄熱傳熱和儲能性能的穩定性外，溫度無疑是另一重要因素.原子的非簡諧振動，溫度的變化引起膨脹或收縮，使原子組成結構和相互作用發生變化，導致一個原子所占面積以及電荷密度電子態發生改變，進而引起量子電容等蓄能性能發生改變.

熱穩定性常用溫度穩定性( Temperature stability) 系數來描述，它反應了物理量隨溫度的波動情況［17］.為了描述石墨烯量子電容的溫度穩定性，普遍采用它的溫度系數表示: 設系統的性能參數為f，熱穩定系數定義為αf=(1/f) ( df/dT).αf愈小，熱性能愈穩定.按此定義，量子電容熱穩定性系數定義為:

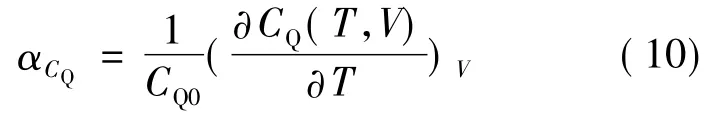
其中，CQ0為T 趨于0 K，V=congst 時的量子電容，按文獻［15］，可取CQ0=1.6 μF·cm-2.將(8) 、(9) 式代入( 10) 式，得到石墨烯量子電容隨溫度和電壓變化的具體表示.

5 原子非諧振動對石墨烯量子電容及熱穩定性變化規律的影響

5.1 石墨烯材料量子電容隨溫度的變化規律

Davydov［13］給出石墨烯零溫時鍵長d0=1.42×10-10m，將文獻［13］的數據代入(1) 式，求得簡諧系數ε0=3.5388 ×102J·m-2，第一非簡諧系數ε1=-3.49725 ×1012J·m-3，第二非簡諧系數ε2=3.20140 ×1022J·m-4.代入(9) 式，得到線膨脹系數αl隨溫度的變化.

最近鄰格點間的交換能t=3 eV，晶格常數a=1.42 ×10-10m，將玻爾茲曼常數、電子電荷等一起代入( 8) 式，求得不同電壓下理想單層石墨烯材料的量子電容( 單位: F·m-2) 隨溫度的變化，如圖2 所示.其中V=0.1 V 時的部分數據如表1 所示.圖中的曲線0、1、2 和表1 中的0、1、2 分別是簡諧近似、計算第一非簡諧項、同時計算第一、二非簡諧項的結果.

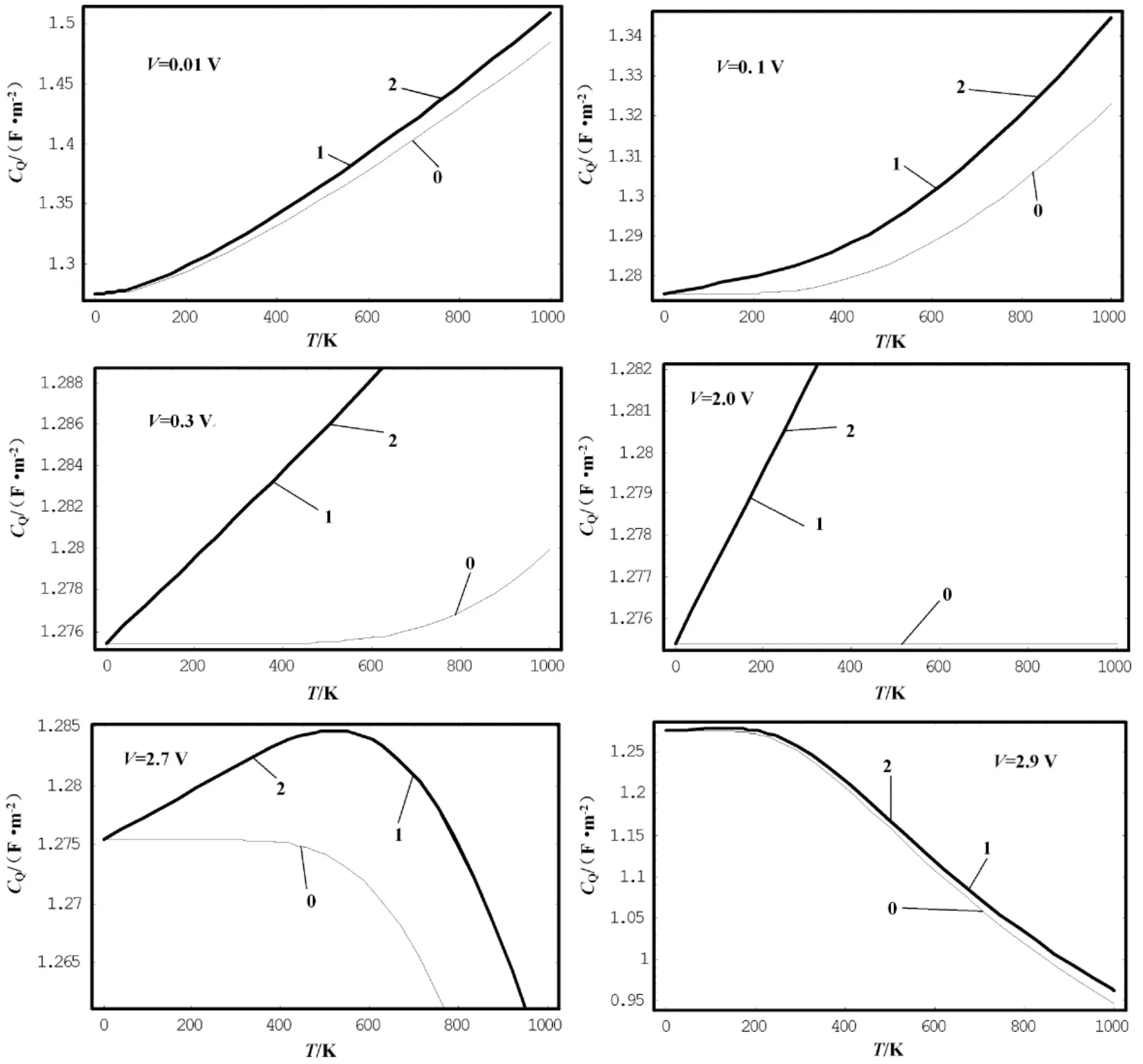
圖2 不同電壓下單層石墨烯材料量子電容隨溫度的變化Fig.2 Changes of the quantum capacitance of a single -layer graphene material with temperature under different voltages

由圖2 和表1 可以看出，( 1) 電壓一定的條件下，單層石墨烯量子電容隨溫度升高發生非線性變化，具體變化情況與電壓有關，電壓小于2.3 V 時，量子電容隨溫度升高而增大; 而電壓高于2.3 V 時，量子電容先隨溫度升高而增大，到達某一溫度值時，反而隨溫度升高而減小.(2) 非簡諧項對量子電容隨溫度的變化規律有重要影響.與簡諧近似相比，考慮到原子非簡諧振動后的量子電容的值有所增大，且溫度愈高，兩者的差愈大，即非簡諧效應愈顯著.例如，當溫度為300 K 時，非簡諧情況的量子電容值比簡諧近似時的值大0.33%; 而當溫度為1 000 K 時，后者比前者大1.47%.( 3) 本文的計算結果不僅在數量級上與文獻［10］的結果( 0.23 F·m-2)接近，而且給出了量子電容隨溫度的變化規律.

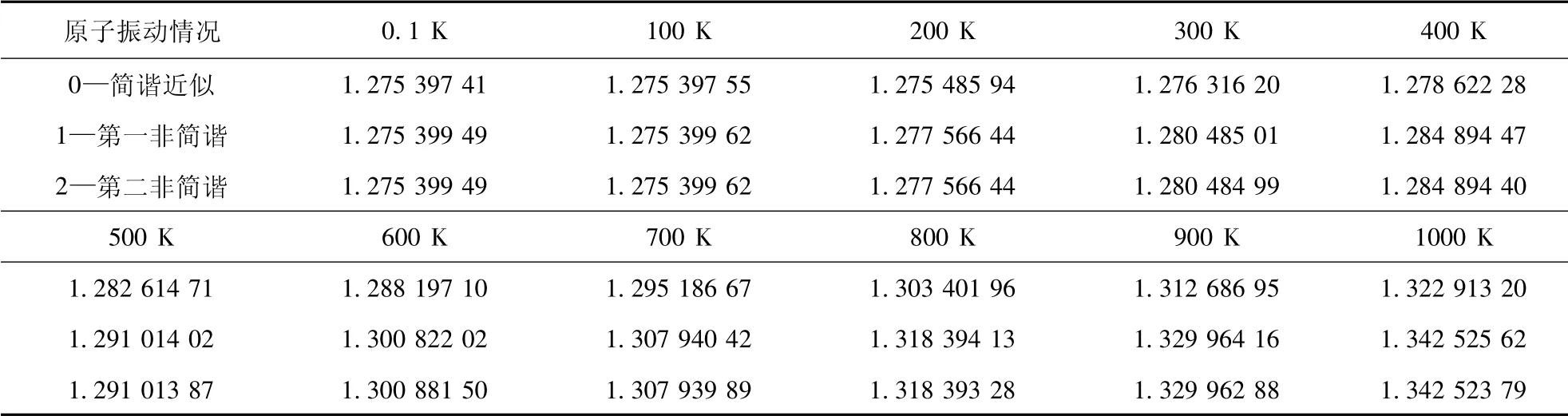
表1 當V=0.1 V 時，簡諧、第一非簡諧、第二非簡諧量子電容隨溫度變化的對比Table 1 Comparison of the changes of simple harmonic，first anharmonic，and second anharmonic quantum capacitances CQ( F·m -2) with temperature at V=0.1 V ( CQ單位: F·m -2)

5.2 石墨烯材料量子電容隨電壓的變化規律

將數據代入(8) 式和( 9) 式，得到溫度為T=300 K 和T=800 K 情況下，石墨烯量子電容CQ隨電壓V 的變化，如圖3 所示，部分數據如表2 所示.圖3 的曲線0、1、2 的含義同圖2.

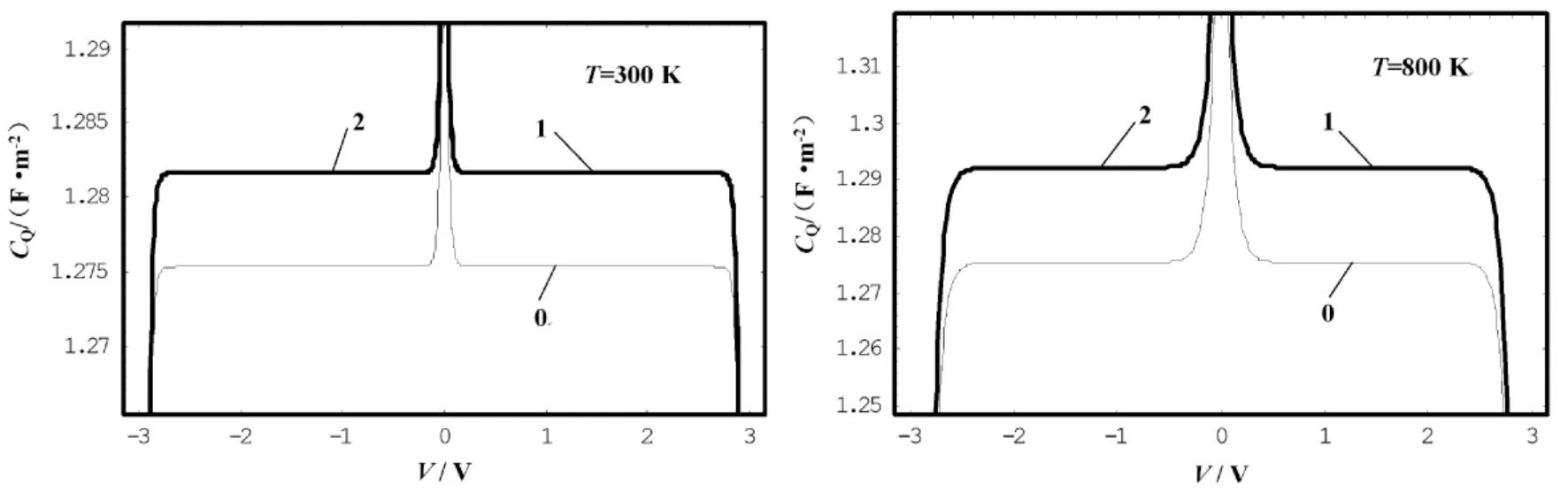
圖3 不同溫度下單層石墨烯量子比電容隨電壓的變化Fig.3 Changes of graphene quantum capacitance with voltage at different temperatures

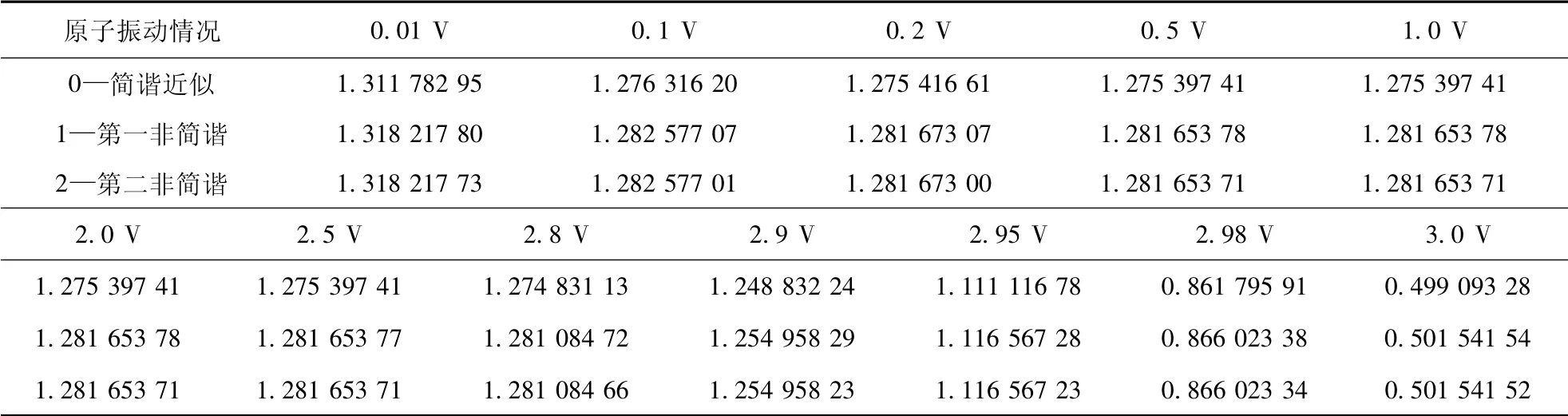
表2 當T=300 K 時，簡諧(0) 、第一非諧(1) 、第二非諧(2) 量子比電容隨電壓的變化Table 2 Changes of graphene quantum capacitance CQ( F·m -2) with voltage at T=300 K( CQ單位: F·m -2)

由圖2 和表1 可以看出，( 1) 給定溫度下，石墨烯量子電容隨電壓的增大產生非線性變化，其中，當電壓值小于0.4 V 時，量子電容由極大值迅速減小，當電壓值在0.4 ～2.8 V 時，量子電容較大幾乎保持不變; 當電壓值大于2.8 V 時，量子電容迅速減小; 電壓值大于3 V 時，量子電容變為0.(2) 與簡諧情況的值相比，非簡諧情況的量子電容值有所增大( 由1.275 F·m-2增大到1.282 F·m-2) ，但曲線的變化趨勢相同，其中，溫度較高時的曲線其變化趨勢較緩慢，曲線較圓滑.

5.3 石墨烯量子電容的熱穩定性的變化規律

將上述數據代入(8) 式和(9) 式，再代入(10)式，就得到不同電壓情況下，石墨烯量子電容的溫度穩定性系數隨溫度的變化，如圖4 所示.圖4 的曲線0、1、2 的含義同圖2.其中V=0.1 V時簡諧0、第一非簡諧1、第二非簡諧2 的部分數據如表3 所示.

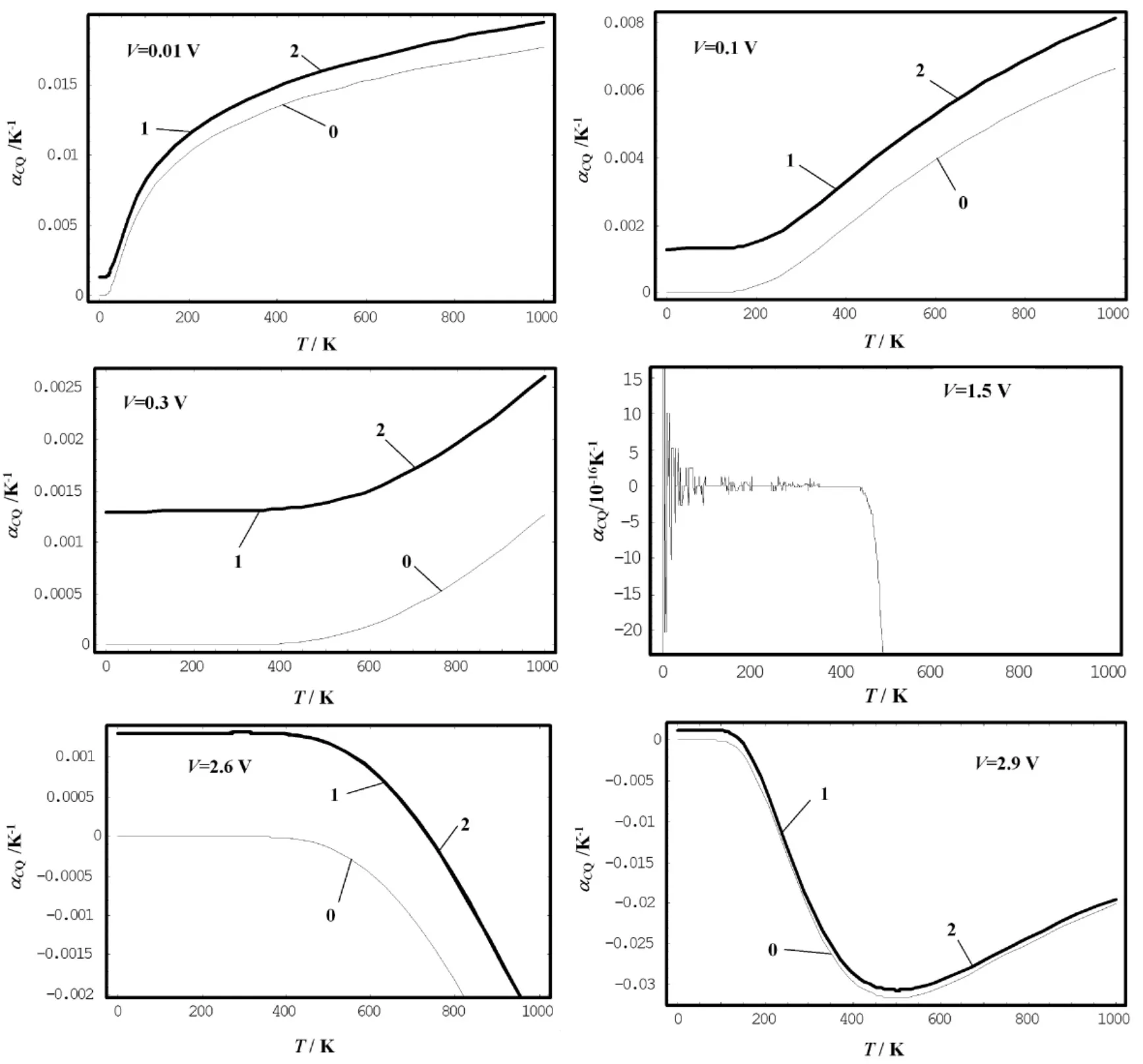
圖4 不同電壓條件下石墨烯量子電容的溫度穩定性系數隨溫度的變化Fig.4 Variations of temperature stability coefficient of graphene quantum capacitor with temperature under different voltage conditions

由圖4 和表3 可看出，( 1) 石墨烯量子電容的溫度穩定性系數隨溫度升高發生非線性變化，具體變化情況與電壓有關.其中，當電壓小于1.5 V 時，其溫度穩定性系數隨溫度升高而由緩慢變化到很快增大; 當電壓大于1.8 V 時，則隨溫度升高而由緩慢變化到很快減小; 當電壓在1.5 ～1.8 V 之間時，變化曲線逐漸發生反向變化; (2) 在電壓在1.5 ～1.8 V 之間，而溫度低于800 K 的情況下，石墨烯量子電容的溫度穩定性系數最小且不隨溫度而變，這表明在此電壓和溫度范圍內，石墨烯量子電容的溫度穩定性最好;(3) 與簡諧近似的值相比，考慮到非簡諧項后，石墨烯量子電容熱穩定性系數有所增大，且增大的情況與溫度有關.例如，在電壓為0.1 V 的條件下，溫度為400 K 時，非簡諧情況的量子電容熱穩定性系數值比簡諧近似的值大67.47 %; 而溫度為1 000 K 時，則大22.36%.這表明非簡諧效應會使石墨烯量子電容熱穩定性比簡諧近似情況變差，即非簡諧效應具有降低量子電容熱穩定性的作用.

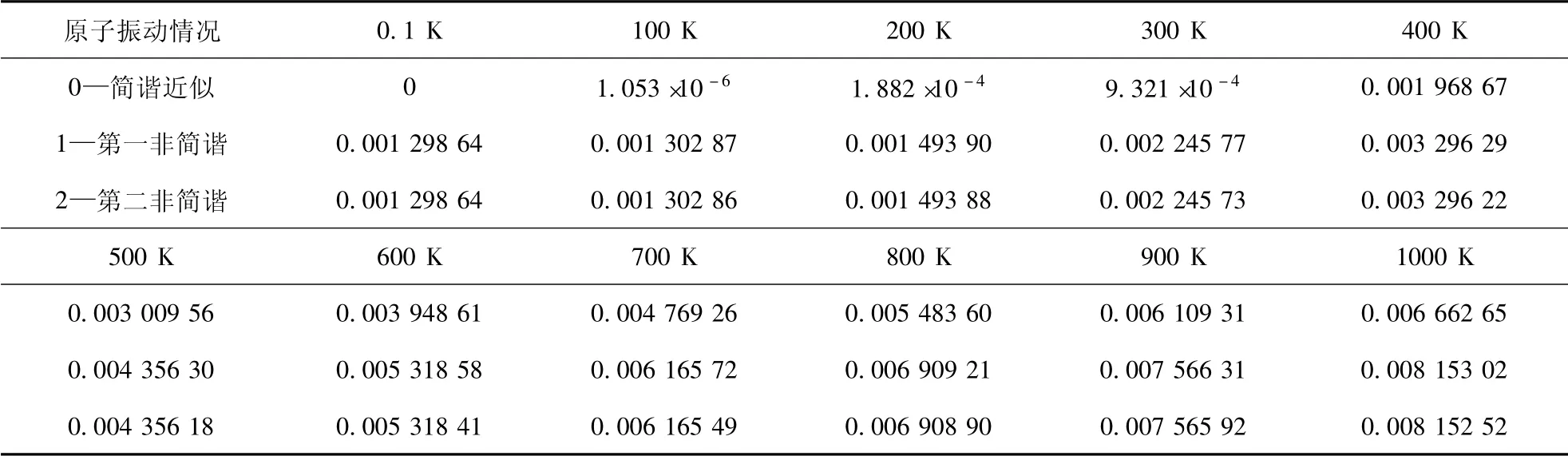
表3 當V=0.1 V 時，不同情況的量子比電容熱穩定性系數αC Q隨溫度的變化Table 3 Changes of thermal stability coefficient αC Q ( K -1) of graphene quantum capacitance with temperature at V=0.1 V( 單位: K -1)

6 結 論

本文的研究給出了石墨烯材料量子電容及其熱穩定性的變化規律，發現都與溫度和電壓有關，具體結果由(8) 式、(9) 式、(10) 式表示.具體描述為:

(1) 當電壓一定時，石墨烯量子電容和它的溫度穩定性系數均隨隨溫度升高發生非線性變化，變化情況與電壓有關.其中，當電壓小于2.3 V時，量子電容隨溫度升高而增大，它的溫度穩定性系數隨溫度升高由緩慢變化到很快增大; 而電壓高于2.3 V 時，量子電容先隨溫度升高而增大，到達某一溫度值時，隨溫度升高而減小，它的溫度穩定性系數隨溫度升高而由緩慢變化到很快減小; 而當溫度一定時，量子電容只在電壓值為0.4 ～2.8 V 范圍內才變化較小，而電壓值大于2.8 V 時，量子電容迅速減小并趨于0.

(2) 與簡諧近似情況相比，非簡諧項會使石墨烯量子比電容有所增大，且溫度愈高，兩者的差愈大，即非簡諧效應愈大.例如，當溫度為300 K 時，非簡諧振動情況的量子比電容值比簡諧近似的值大0.33%; 而溫度為1 000 K 時，則非簡諧情況大1.47%.

(3) 與簡諧近似的值相比，非簡諧項會使石墨烯量子比電容熱穩定性系數有所增大，其中溫度為400 K 時，非簡諧情況的熱穩定性系數值比簡諧近似的值大67.47%，而溫度為1 000 K 時，則非簡諧情況大22.36%.非簡諧效應會使石墨烯量子電容熱穩定性比簡諧情況變差，即非簡諧效應會降低量子電容熱穩定性的作用.

(4) 電壓在1.5 ～1.8 V 之間，而溫度低于800 K 的情況下，石墨烯量子電容的溫度穩定性系數最小且不隨溫度而變，此時石墨烯量子電容的溫度穩定性最好.

本文所得有關量子電容的結果不僅與已有文獻的結果接近，而且還給出了量子電容和它的溫度穩定性系數隨溫度的變化規律，這對石墨烯在超級電容器儲能性能上的應用是有參考價值的.