擴展Su-Schrieffer-Heeger模型在周期性邊界條件下的相變

尹傳磊， 朱學峰， 楊非凡， 李 蓉， 周毅堅， 彭文博， 趙 洋

(河南科技大學 物理工程學院 河南省光電儲能材料與應用重點實驗室，洛陽 471023)

1 引 言

Su-Schrieffer-Heeger (SSH)模型是一種用來描述一維聚乙炔的緊束縛模型，具有十分優美的數學結構[1]. 近年來關于拓撲絕緣體[2,3]的研究，引起了人們對 SSH模型的廣泛關注. 更值得關注的是，由于 SSH模型具有多種物理現象[4-8]，特別是其不平庸的拓撲相位[9,10]，人們對 SSH模型的研究日益深入. SSH模型可以作為一維聚乙炔[1]、石墨烯絲帶[11]、非對角雙色光晶格[12]和p軌道光學階梯系統[13]等多種系統的數學投影. 然而上述文章大多是關于 SSH模型所表現出的量子狀態，很少有關于 SSH模型熱力學性質的文章[14,15]. 此外，文獻[14]中熱容對溫度的依賴性與文獻[15]中的不同. 更值得注意的是， Zoli的計算沒有介紹二聚化[14]. 在計算擴展后的 SSH模型的熱力學特性時，由于不含二聚化的 SSH模型不能用來描述聚乙炔，因此在計算擴展SSH模型的熱力學特性時，二聚化不應該被忽略.

本文利用統計力學方法和費曼路徑積分方法，研究了含三個過渡項的擴展 SSH模型在周期性邊界條件下的熱力學性質. 在這項工作中不涉及定壓熱容，所以文中所用熱容均為指定熱容. 根據統計力學的一般表述，一個系統的熱力學性質可以由它的配分函數得出[16]. 而該配分函數又可以通過費曼路徑積分表述[17]. 此外，在zoli的研究中[14]，配分函數由費曼路徑積分得到. 又因為該模型的配分函數可以用一個連乘來表示，所以其亥姆霍茲自由能、熵、內能、熱容均可用求和的方式進行表述. 文章用圖解法，解釋了模型ⅰ的熱容與溫度的比率(HCOTR)對溫度的依賴性，并解釋了擴展的 SSH模型(模型ⅱ)只包含兩種躍遷項(NN, NNN躍遷項)和只包含一種躍遷項(NN躍遷項)的 SSH模型(模式識別)[1]對溫度的依賴性.

2 理論模型

一個原胞包含a和b兩個格點的一維晶格的哈密頓量是[1, 9, 10]

H=HSSH+HNNN+HNNNN

(1)

其中

(2)

(3)

(4)

這里t1=t+ε和t2=t-ε均是原胞中的躍遷幅度，ta是沿著a子格的躍遷幅度，tb是沿著b子格的躍遷幅度，ca,n(或者cb,n)是a(或者b)子格中的湮滅算符，t3和t4是NNNN躍遷幅度. 為了簡化模型，將t=1作為能量的單元[9, 10].

(5)

(6)

根據矩陣理論的方法，我們得到了矩陣h(k)的特征值

(7)

其中

(8)

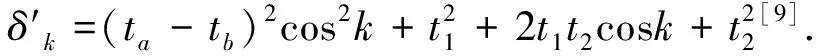
3 結果與討論

模型ⅰ的配分函數可以表示為費曼路徑積分的形式

(9)

其中歐幾里德作用量

(10)

泛函積分的測度

(11)

且

(12)

(13)

且該場可以用傅里葉級數表示

其中松原頻率為

(14)

l屬于所有整數的集合. (9)式表示的配分函數可以寫為

(15)

其中測度

(16)

且作用量

(17)

通過計算路徑積分(15)，得到了模型ⅰ的配分函數

(18)

這里Z±(k)=1+e-βE±(k). 模型ⅰ配分函數的自然對數乘-T，得到它的亥姆霍茲自由能

(19)

利用熱力學關系，得到它的熵

(20)

和內能

(21)

通過算其內能對溫度的偏導數，我們得到它的熱容

(22)

圖1(a)和(b)顯示了模型ⅰ(由實線表示)、模型ⅱ(由點線表示)、模型ⅲ(由短劃線表示)的HCOTR的溫度依賴性.

為了獲得圖1,我們設置ε=0.065、ta=0.5、tb=0.6、t3=0.08、t4=0.08. 當溫度由絕對零度逐漸升高時：模型ⅱ和模型ⅲ的HCOTR均呈現出先增大后減小再增大的趨勢，而模型ⅰ的HCOTR先減小，在達到最小值后增大. 在低溫(0-0.3)下每個模型都有一個HCOTR的極值，如圖1 (a)所示. 模型ⅱ的極值低于模型ⅲ的極值，但高于模型ⅰ的極值.

由于HCOTR在低溫下隨溫度增加而上升是玻璃態的特殊性質，所以這三個極值點是三個相變點[14,18]. 如圖1(a)所示，模型ⅰ的相變溫度低于模型ⅱ的相變溫度，且模型ⅱ的相變溫度低于模型ⅲ的相變溫度. 這表明躍遷項可以降低相變溫度.

在極低溫度下，模型ⅱ和模型ⅲ的HCOTR都隨著溫度升高而增大，而模型ⅰ的HCOTR隨溫度升高而降低. 模型ⅰ和其他兩種模型HCOTR的單調性之間的這種差異，根本原因是NNNN躍遷項.

圖1 模型ⅰ(由實線表示)，模型ⅱ(由點線表示)與模型ⅲ(由短劃線表示)的HCOTR隨溫度增加而變化的曲線. 每條曲線的ε值都設定為0.065，ta值都設定為0.5，tb值都設定為0.6，t3值都設定為0.08，t4值都設定為0.08.(a)和(b)除溫度域不同外，其它參數均相同.Fig. 1 HCOTR curves of model ⅰ (represented by the solid line), model ⅱ (represented by the dotted line) and model iii (represented by the dashed line) with increasing temperature. The value of each curve is set to 0.065, the value of ta is set to 0.5, the value of tb is set to 0.6, the value of t3 is set to 0.08, and the value of t4 is set to 0.08. (a) and (b) except for the difference in temperature range, other parameters are the same ones.

如圖1(b)所示，在高溫(0.3～1)下這三種模型的HCOTR的溫度依賴性相似，當溫度由0.3逐漸升高時：這三種模型的HCOTR均先增大，在達到極大值后減小. 在高溫(0.3～1)下模型ⅱ的最大HCOTR高于模型ⅲ的HCOTR，而低于模型ⅰ的HCOTR.

在圖2(a)和(b)描繪的是在ε取四個不同值時模型ⅰ的HCOTR的溫度依賴性，其中實線對應ε=0、點線對應ε=0.15、點劃線對應ε=0.065、短劃線對應ε=0.3 . 為了獲得圖2，我們設置ta=0.5、tb=0.6、t3=0.08、t4=0.08 . 如圖2(b)所示，在高溫(0.3～1)下模型ⅰ中的ε取四個不同值時HCOTR有類似的溫度依賴性且HCOTR的最大值隨ε減少而增加；當溫度由0.3逐漸升高到1時，這四個ε值對應的HCOTR都先增大,到最大值后減小.

然而如圖2(a)所示，在極低溫(0-0.05)下不同ε值對應的HCOTR的單調性不同，這表明NN躍遷項會影響模型ⅰ的HCOTR的單調性.ε=0.3時模型ⅰ有兩個相變點，這表明NN躍遷項會影響模型ⅰ的相變.

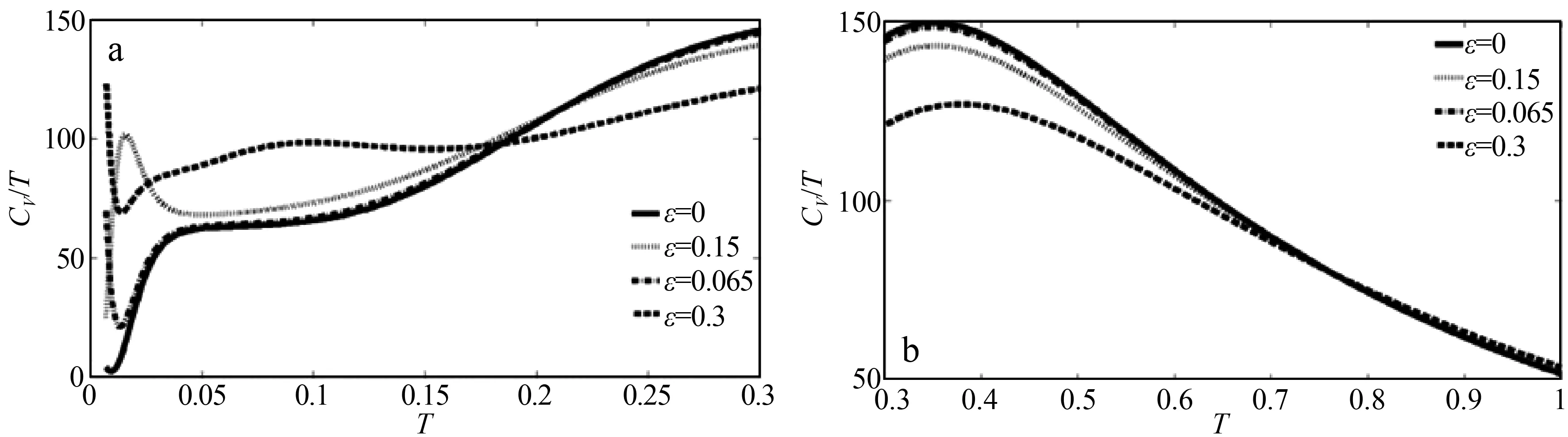
圖2 在ε取四個不同值時模型ⅰ的HCOTR的溫度依賴性. 實線對應ε=0；點線對應ε=0.15；點劃線對應ε=0.065；短劃線對應ε=0.3. 對于每條曲線，ta值都設定為0.5，tb值都設定為0.6，t3值都設定為0.08，t4值都設定為0.08. (a)和(b)除溫度域不同外，其它參數均相同.Fig. 2 The temperature dependence of the HCOTR of model i when four different values ε are used. The solid line corresponds to ε=0; the dotted line corresponds to ε=0.15; the dash dot line corresponds to ε=0.065; the dashed line corresponds to ε=0.3. For each curve, the ta value is set to 0.5, the tb value is set to 0.6, the t3 value is set to 0.08, and the t4 value is set to 0.08. (a) and (b) except for the difference in temperature range, other parameters are the same ones.

圖3(a)和(b)顯示了在ta、tb取四組不同值時模型ⅰ的HCOTR的溫度依賴性. 實線對應ta=0.3、tb=0.5，點線對應ta=0.2、tb=0.7，點劃線對應ta=0.6、tb=0.3，短劃線對應ta=0.8、tb=0.3. 為了獲得圖3，我們設置ε=0.065、t3=0.08、t4=0.08. 如圖3(b)所示，在高溫(0.3～1)下模型ⅰ中的ta、tb取四組不同值時HCOTR有類似的溫度依賴性. 當溫度由0.3逐漸升高到1時，這四組ta、tb值對應的HCOTR都先增大，到最大值后減小.

然而如圖3(a)所示，在低溫(0.3-1)下不同ta、tb值對應的HCOTR的單調性不同，這表明NNN躍遷項會影響模型ⅰ的HCOTR的單調性.ta=0.2、tb=0.7時模型ⅰ有兩個相變點，這表明NNN躍遷項可以影響模型ⅰ的相變.

圖4(a)和(b)描繪了在t3、t4取四組不同值時模型ⅰ的HCOTR的溫度依賴性. 實線對應t3=0.08、t4=0.08，點線對應t3=0.01、t4=0.07，點劃線對應t3=0.06、t4=0.01，短劃線對應t3=0.08、t4=0.03 . 為了獲得圖4，我們設置ε=0.065、ta=0.5、tb=0.6 . 在高溫(0.1～1)下模型ⅰ中的t3、t4取四組不同值時HCOTR有類似的溫度依賴性. 當溫度由0.1逐漸升高到1時，這四組t3、t4值對應的HCOTR均先增大到最大值后減小.

然而如圖4(a)所示，在低溫(0-0.1)下不同t3、t4值對應的HCOTR的單調性不同，這表明NNNN躍遷項會影響模型ⅰ的HCOTR的單調性.

4 總 結

利用統計力學的一般表述和費曼路徑積分，計算了模型ⅰ在周期性邊界條件下的熱力學性質. 對模型ⅱ和模型ⅲ也進行了類似的計算并與模型ⅰ作對比. HCOTR對溫度的依賴曲線有最小值點表明這三種模型均存在相變.在低溫下，每個模型都有相變且躍遷項可以降低相變溫度. 在極低的溫度下，NNNN躍遷項可以引起模型ⅰ與其他兩種模型在HCOTR的單調性方面的差異. 在低溫下，NN、NNN、NNNN三種躍遷項都可能影響模型ⅰ的HCOTR的單調性. NN或NNN躍遷項可以影響模型ⅰ的相變.

圖3 在ta、tb取四組不同值時模型ⅰ中的HCOTR的溫度依賴性. 實線對應ta=0.3、tb=0.5；點線對應ta=0.2、tb=0.7；點劃線對應ta=0.6、tb=0.3；短劃線對應ta=0.8、tb=0.3. 對于每條曲線，ε=0.065、t3=0.08、t4=0.08.(a)和(b)除溫度域不同外，其它參數均相同.Fig. 3 The temperature dependence of HCOTR in model i when ta and tb take four different values. The solid line corresponds to ta=0.3, tb =0.5; the dotted line corresponds to ta=0.2, tb=0.7; dash dot line corresponds to ta=0.6, tb=0.3; the dashed line corresponds to ta=0.8, tb=0.3. For each curve, ε=0.065, t3=0.08, t4=0.08. (a) and (b) except for the difference in temperature range, other parameters are the same ones.