立體幾何最值問題的四個常見幾何視角

廣東省廣州市廣州開發區外國語學校 (510700) 蔡軍喜

最值問題作為動態立體幾何問題最典型的類型，將空間立體幾何中的核心知識和方法融入其中，能有效甄別綜合立體幾何的數學素養，歷來都受到命題者的青睞．對于定量化的動態立體幾何問題，構建函數、三角、不等式模型是解決問題常用的途徑，利用向量或者幾何邊角關系構造函數、三角、不等式是解答此類問題的基本策略.但在實際操作中，很多問題需要預先構建幾何變換，挖掘幾何本質，才能順利實現代數化處理.本文歸納常見的四種幾何變換視角，供參考.

1 展開

圖1

例1 (2018全國卷Ⅰ)某圓柱的高為2，底面周長為16，其三視圖如圖1．圓柱表面上的點M在正視圖上的對應點為A，圓柱表面上的點N在左視圖上的對應點為B，則在此圓柱側面上，從M到N的路徑中，最短路徑的長度為( ).

圖2

圖3

解析：由三視圖可知，該幾何體為如圖2所示的圓柱，該圓柱的高為2，底面周長16．畫出該圓柱的側面展開圖，如圖3所示，連接MN，則MS=2，SN=4，則從M到N的路徑中，最短路徑的長度為

點評：兩點間直線距離最短，運用這一原理，將立體圖形沿某條棱展開成平面圖形，化曲為直，化空間為平面是求解此類線段和最值問題的通性通法。需要注意的是同一個幾何體沿不同方向展開的情況最值可能會有所不同。

圖4

例2 (2006江西卷)如圖4，已知正三棱柱的底面邊長為1，高為8，一質點自點A出發，沿著三棱柱的側面繞行兩周到達點A1的最短路線的長為.

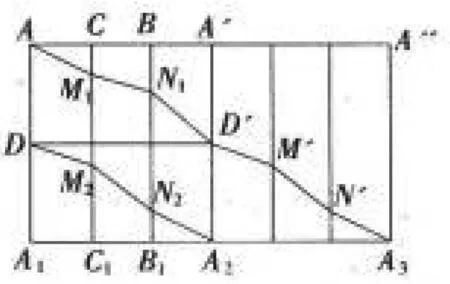
圖5

解析：將三棱柱側面沿棱AA1展開得矩形AA1A2A，因沿側面繞行兩周.故將這個矩形向右平移3個單位與原矩形拼接在一起，如圖5所示，因為平面內兩點之間距離最短.故所求的最短距路線的長就是大矩形對角線的長.由勾股定理可得對角線長為10.

點評：對棱柱進行側面展開，化空間為平面，化折為直，再將展開圖平移、拼接，使分散的兩條折線連在一起.從而使問題得到非常直觀的解決.

2 旋轉

圖6

點評：本題本質仍是空間問題平面化，化折為直，不同的是需將兩個平面分別繞軸旋轉到與第三面共面，從而實現平面內多點共線后的兩點間直線距離最短.將多面體的兩個面中的一個面沿著它們的公共邊翻折或旋轉，使這兩個面共面，從而使位于這兩個平面內的幾條線段位于同一平面內，這樣就將空間問題轉化為平面幾何問題，多個面的情形也可類似處理，這既是降維的思想，也是翻折與旋轉，變與不變的核心.

3 對稱

例4 (2020廈門市一模)已知正三棱柱ABC-A1B1C1的所有棱長均為2，點M,N分別在側面ABB1A1和ACC1A1內，BC1和B1C交于點P，則ΔMNP周長的最小值為.

圖7

解析：如圖7，設點P關于側面ABB1A1和ACC1A1的對稱點分別為Q,R，連接QR，則當點M,N,Q,R共線時，ΔMNP周長最小，由于在正三棱柱ABC-A1B1C1中，點P是BC1和B1C的交點，所以點P是側面BCC1B1的中心，故ΔMNP周長最小時，M,N分別是側面ABB1A1和ACC1A1的中心，所以ΔMNP周長的最小值為3.

點評：兩個動點，三條線段，單純從代數角度構建函數關系，數式和運算異常復雜，而通過挖掘幾何特質，在變化中尋找不變量，點P確定，側面ABB1A1和ACC1A1固定，對稱與平移，動中覓定，變與不變相隨.

4 割補

例5 (2010全國卷)已知在半徑為2的球面上有A,B,C,D四點，若AB=CD=2,則四面體ABCD的體積的最大值為( ).

圖8

解析：

圖9

點評：借助常見的幾何“母體”，通過還原與補形，使不規則的幾何體有體可依，化“無形”為“有型”.同時，平面幾何中常見的基本結論: (1)連結兩點的線中線段最短; (2) 直線外一點與直線上各點的連線中,垂線段最短.實現聯系遷移，有據可依.

圖10

例6 (2012上海卷)如圖10所示，AD與BC是四面體ABCD中互相垂直的棱,BC=2,若AD=2c，且AB+BD=AC+CD=2a，其中a,c為常數，則四面體ABCD的體積的最大值是.

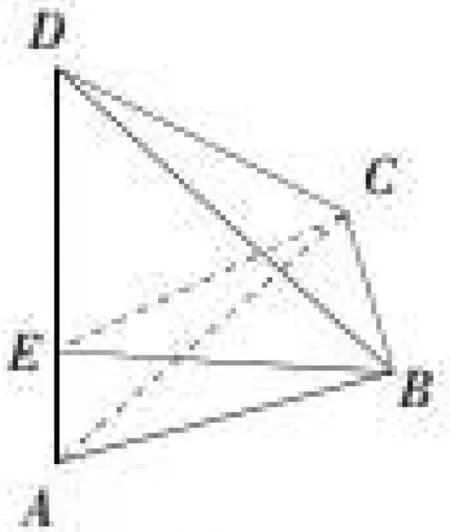
圖11

動態立體幾何的問題千變萬化，有在變化過程中分析空間元素的位置，有在變化中求解某個量的最值或范圍，有在變換中分析某個點的軌跡等等．只要我們用心去理解問題，探尋解決問題的方法，反思和總結問題解決的一般性策略，數形相依，動靜結合，幾何代數互譯，那么，我們自然就提高了解決問題的效率，數學思維與視角也會長足進步，更能在問題解決過程中享受數學探究的樂趣．