中日高中數學教材概率與統計的比較研究

覃淋 喻曉婷 張靜

【摘要】以“概率與統計”作為研究對象，對中日兩國高中數學教材進行比較研究.研究發現：中國教材知識點數量多于日本教材;兩套教材中概率內容都多于統計內容;中國教材比較注重定義的嚴格性，日本教材比較注重數學知識的內部聯系;兩套教材都強調數學的應用，注重將計算機融入教材.

【關鍵詞】數學教材;概率與統計;比較研究;計算機

教材為教師的教與學生的學提供學習主題、基本線索和具體內容，為學校的教與學活動提供了基本范例、基本思路和基本方法，是實現數學課程目標、發展學生數學學科核心素養重要的教學資源＼[1＼].考查歷史上重要的數學教育改革，我們可以發現教材改革是數學教育改革的中心問題之一，如由美國引領，最后幾乎波及全球的新數學運動＼[2＼].教材作為教師教、學生學的主要依據，其質量會直接影響教學效果.對教材進行分析和比較，是為了更好的利用教材，充分發揮教材在教學活動過程中的價值，使教師能創造性的使用教材，更好地為教師的教與學生的學服務.

本文之所以選取概率與統計作為研究對象，主要基于以下原因：首先，隨著社會的發展，概率與統計在人們的生活中扮演著越來越重要的角色，概率與統計的基礎知識已經成為一個未來公民的必備常識，概率與統計素養是現代社會每一個人應該具備的基本素養.其次，概率與統計在各國的中小學數學課程中占據重要地位，是我國數學課程改革變化較大的內容之一，是《普通高中數學課程標準（2017年版2020年修訂）》（以下簡稱《標準》）中特別加強的內容，也是我國高中數學教學中的“弱項”，其思維方式和代數、幾何等傳統數學教學內容不同.最后，中小學數學教師對概率與統計的認識和理解不是很深刻，我國高中數學教師的概率統計知識儲備不足，大部分教師對概率統計的基本概念理解深度不夠＼[3＼].本文研究中日兩國高中數學教材中概率與統計的內容設置以及重要知識點的處理，希望能為我國高中數學教材概率與統計的編寫提供一些參考.

1 研究對象

考慮教材的使用范圍以及教材能否體現所在地區數學課程標準的理念，結合教材的出版時間，確定了研究對象＼[48＼].

2研究結果

2.1知識點的比較

根據我們所選擇的教材，統計了兩套高中數學教材中概率與統計的知識點及其數量，結果如下（“+”表示有此知識點，“-”表示無）

高中數學學習的概率知識主要有概率、隨機變量及其分布、隨機變量的數字特征、條件概率、全概率公式和一些常見的概率分布.統計知識有收集數據和分析數據兩方面，前者是抽樣調查，包括隨機抽樣等內容;后者是統計推斷，包括假設檢驗、線性回歸分析等.

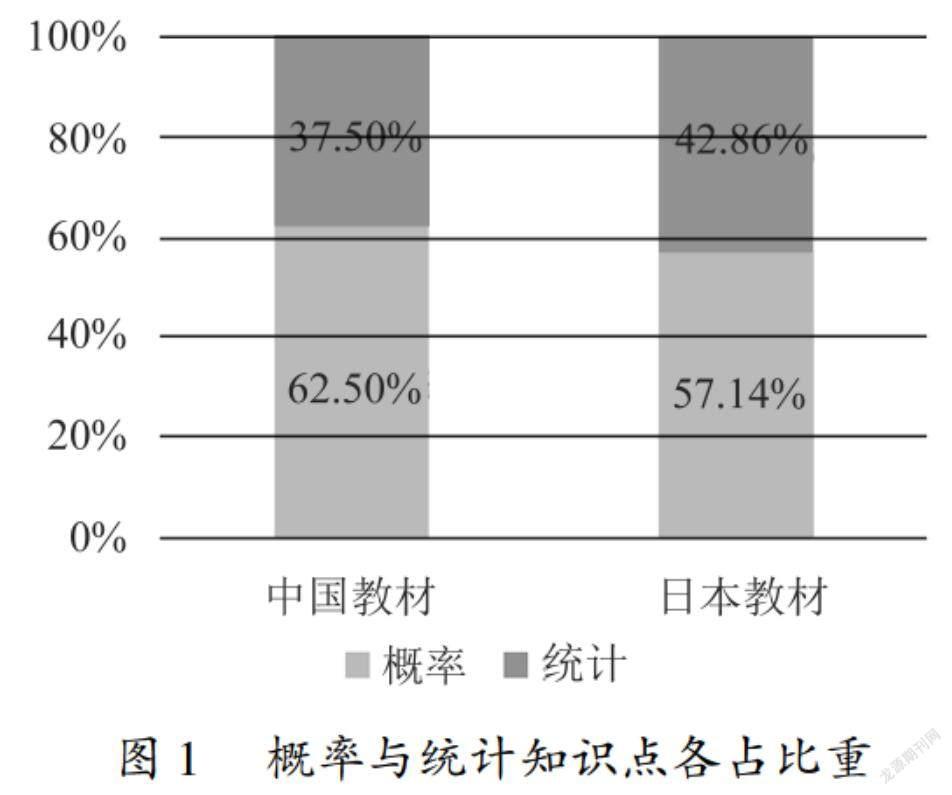
由表2，我們總共列出了46個知識點.在知識點數量上，中國教材多于日本教材，有40個;日本教材有35個.對兩套教材中概率與統計知識點數量進行統計，計算各自所占比重.得到如圖1的結果.

由圖1知，中國教材中概率與統計知識點數量分別為25、15，所占比例分別為62.5%、37.5%;日本教材中概率與統計知識點數量分別為20、15，所占比例分別為57.14%、42.86%.具體知識點的差異見表3.由表3知，在概率與統計內容知識點的選擇上，日本教材中有些內容，如統計數據的計算機處理、大數定律、隨機變量的和與積等是中國教材沒有的.具體來看，首先是概率部分，和日本教材相比，中國教材介紹的內容較多，如全概率公式和貝葉斯公式、兩點分布以及超幾何分布等內容，日本教材均未涉及.其次，在統計部分，描述性統計方面，兩套教材的知識點僅有細微差別;在推斷性統計內容方面，中國教材就涉及較少，與日本教材差別較大.

2.2知識點處理的比較

首先，從內容模塊的編排順序看，兩套教材的順序都是“統計—概率—概率—統計”，和03版實驗教材的順序一樣.與03版實驗教材相比，中國教材增加了較多的內容（刪除了系統抽樣和幾何概型），不管是知識廣度上，還是內容深度上，都大大增加了.其次，從教材對具體知識點的處理看，中國教材對有些知識僅簡單加以介紹.比如正態分布，中國教材以問題引入的形式介紹了正態分布，討論了正態分布密度曲線的特點以及均值、標準差對正態分布的影響.還以文本框旁白的形式簡單介紹了正態分布的歷史，利用Excel中的NORM DIST函數來計算P（X≤x）.日本教材除上述內容外，還介紹了連續性隨機變量的概率密度函數、正態分布的應用，二項分布當樣本量足夠大時，趨近于正態分布.從內容表述上看，兩套教材都比較注重數學學科內部知識的聯系，強調數學的整體性.

下面以概率的定義、數據分析兩個核心主題為例來討論.

2.2.1概率的定義

高中數學教材中對于概率這個概念的討論，一般會介紹概率的“統計定義”和“古典定義”，但不同教材在處理方式上有所不同.“古典定義”是在等可能性的基礎上給出的.假設一個試驗有N個等可能出現的結果，對于事件A來說，它恰好包含了這個試驗中的M個結果，那么事件A發生的概率記為P（A）=MN＼[9＼].比如擲硬幣，在硬幣質地絕對均勻的情況下，正反面出現的概率一樣的，都是12;如果我們把擲一次硬幣出現正面記為事件A，那么事件A發生的概率就是P（A）=12.概率的“統計定義”是一種通過試驗去估計隨機事件概率的方法.直觀來說，就是一個隨機事件出現的可能性的大小，可以通過多次重復試驗中這個事件發生的頻繁程度去刻畫＼[9＼].歷史上有許多這樣的試驗，如03版實驗教材中介紹的擲硬幣試驗.

中國教材先是介紹了隨機試驗、樣本點、樣本空間等概念，再用樣本空間和集合定義了隨機事件、必然事件、不可能事件等內容.之后給出了概率的定義＼[4＼]：“對隨機事件發生的可能性大小的度量（數值）稱為事件的概率.”然后給出了古典概型的定義，接著討論古典概型中隨機事件發生概率的計算.在給出計算公式后，以文本框旁白的形式簡要介紹了古典概型的歷史.隨后，中國教材又以一節的內容討論了頻率與概率，首先給出了學習本節內容的必要性：“現實世界中，很多試驗的樣本點往往不是等可能的.”接著，以“探究”活動的形式來討論頻率與概率的關系，讓學生通過分組拋硬幣來得到結論：“一般地，隨著試驗次數的增大，頻率偏離概率的幅度會縮小，即事件A發生的頻率fn（A）會逐漸穩定于事件A發生的概率就是P（A）.”在這段文字的右邊，以圖文旁白的形式介紹了雅克布·伯努利.

日本教材也介紹了概率的兩種定義，但在處理方式上有很大不同.首先介紹了隨機事件的概念，接著介紹拋硬幣的試驗，給出了概率的“統計定義”：“一般地，在大量重復進行同一試驗時，事件A發生的頻率mn總是接近于某個常數，在這個常數附近波動，我們把這個常數稱為事件A發生的概率，記作P（A）.”在給出了概率的“統計定義”后，引入了具有等可能性的事件，在此基礎上把概率的“古典定義”作為計算隨機事件概率的方法給出.這種處理方式和我國《全日制普通高級中學數學教學大綱（試驗修訂版）》下的教材是一樣的.

兩套教材在本內容知識點的編排和處理上有共性也有差異.首先，知識點的選取上，中國和日本教材都介紹了概率的兩種定義.其次，從知識點編排順序看，中國教材是先介紹古典定義，后統計定義;日本教材是先統計定義，再古典定義.最后，在知識點的處理上，中國教材和日本教材在概率的“古典定義”的處理上是相似的，但在概率的“統計定義”的處理上不一樣.

2.2.2數據分析

高中學習的統計內容主要包括收集數據和分析數據兩部分.在通過隨機抽樣得到數據后，就需要對數據進行處理.得到的樣本數據可進行單變量分析（描述性統計量的計算以及統計圖表繪制）與多變量分析（相關性分析、線性回歸分析）.

首先，從兩套教材涉及的內容看，中國教材主要有：總體、樣本、頻率分布直方圖、百分位數、平均數、中位數、眾數、極差、方差、標準差、數據的標準化;散點圖、線性相關、最小二乘法、回歸直線、獨立性檢驗.日本教材主要有：總體、樣本、平均數、中位數、眾數、極差、方差、標準差、統計數據的計算機處理;散點圖、相關系數、中心極限定理等.可以看出，在描述性統計量的討論上，兩套教材的內容差不多，不同的是日本教材專門用了一節內容來討論利用Excel來計算描述性統計量.

其次，從兩套教材對內容的處理來看，兩套教材的大體框架也不一樣，就描述性統計量的討論而言，中國教材和日本教材是放在必修內容中，對多變量分析這一內容，中國教材是屬于選擇性必修的，日本教材是放在選修部分.中國教材一共用了5節來分別介紹這兩部分內容.先是介紹了利用頻率分布表和頻率分布直方圖對隨機抽樣得到的數據進行描述和表示，得到總體的取值規律.接著討論了總體百分位數的估計和用樣本的數字特征（平均數、中位數、眾數、方差、標準差等）估計總體的集中趨勢和離散程度.正文之后，在“閱讀與思考”中以案例的形式介紹了統計學的應用.但沒有引入中心極限定理、置信區間等內容來說明怎樣對“樣本估計總體”的可接受性做出判斷.在選擇性必修部分，以一章的內容討論了“成對數據的統計分析”，先介紹兩個數據之間的相關性，接著介紹了一元線性回歸模型及其應用，以及兩個分類變量的獨立性檢驗.對于描述性統計量的討論，日本教材專門用了一章來討論.先是介紹了一些描述性統計量，如平均值、眾數、中位數、極差、方差等，然后討論了兩變量之間的相關關系，最后介紹了用Excel來計算這些描述性統計量以及相關系數.

總的來說，在本內容中，中國教材在知識點數量上比較多，但在內容深度上不夠深入.日本教材知識點數量較少，在內容深度上也低于中國教材.雖然《標準》中大力強調要“發展學生應用數學的意識”，但從教材內容的編排來看，力度還不夠.相比而言，中國教材還是更強調對基礎知識的掌握，概率與統計是數學中應用性很強的分支，尤其是統計.隨著我國經濟與社會的發展對統計的需求，統計學在2010年已經上升為與數學并列的一級學科，其應用范圍已經涉及到現代社會以及人們日常生活的各個方面.美國著名統計學家C.R.勞認為，“在終極的分析中，一切認識都是歷史;在抽象的意義下，一切科學都是數學;在理性的基礎上，所有的判斷都是統計學.”＼[10＼]統計的重要性由此可見一斑.教師在教學中強調對統計思維體會的同時，也應該重視運用統計方法結合統計軟件來處理一些簡單的實際問題，培養學生的應用意識，引導學生“會用數學的眼光觀察世界，會用數學的思維思考世界，會用數學的語言表達世界”.

2.3對學生能力培養的比較

2.3.1計算能力

我們認為計算能力至少應該包括以下三個方面：一是筆算能力，二是計算工具的使用，三是編程要求（在概率與統計中，表現為統計軟件的使用：計算機模擬和數據分析）.對學生計算能力的培養也應考慮這幾個方面.

中國教材中，幾乎沒有涉及編程.在簡單隨機抽樣部分介紹隨機數法時，介紹了用Excel和R軟件來產生隨機數.在“隨機抽樣”一節中，以“信息技術應用”的形式介紹了Excel和R軟件的簡單統計功能：產生隨機數、隨機抽樣和統計量的計算.在選擇性必修3中，以“信息技術應用”的形式介紹了用GeoGebra畫二項分布、超幾何分布、正態分布的概率分布圖.

統計是關于數據收集和分析的科學，一般包括收集數據和分析數據兩部分.兩套教材都涉及了這兩方面的內容.通過隨機抽樣或實驗設計得到數據后，需要對得到的數據進行整理分析，以此來推斷總體的情況，這是進行統計推斷的主要目的，也是高中數學統計教學的主要目的之一.學會利用計算機對統計數據進行處理，是對學生計算能力培養的重要組成部分.《標準》中也要求“運用計算器、計算機進行模擬活動，處理數據”.

國際上有專門為中小學統計教學而開發的統計教學軟件——Fathom動態數據軟件、TinkerPlots動態數據軟件等.這樣的統計教學軟件是可以也能夠引入到中小學概率統計教學中的.這對改善統計教學，發展學生的數據分析能力和數學應用意識大有裨益.美國《統計教育評價和教學指導綱要》（Guidelines for Assessment and Instruction in statistics Education）指出：信息技術改變了統計學家的工作方式，也應該改變他們的教學方式.……信息技術應該被用于分析數據，讓學生聚焦于對數據結果的解釋和條件的檢驗，而不是單純的計算.……信息技術也可以用于幫助學生將概念可視化，通過模擬發展對抽象概念的理解＼[11＼].

2.3.2發現、提出、分析和解決問題的能力

《標準》中明確指出，要提高學生“從數學角度發現和提出問題的能力、分析和解決問題的能力”，但從教材概率與統計部分的內容看，由于知識之間的關聯性不好，使學生無法對相關問題進行質疑，從而影響對學生提出問題能力的培養.因為“對于任何一門科學的正確概念，都不能從有關這門科學的片斷知識中形成，盡管這些片斷知識足夠廣泛.還需要對這門科學的整體有正確的觀點，需要了解這門科學的本質”＼[12＼].

“用樣本估計總體”屬于統計推斷的內容，中國教材和日本教材的處理方式明顯不同.中國教材在介紹用樣本頻率分布估計總體分布、總體百分位數的估計、總體集中趨勢的估計（平均數、中位數、眾數）和總體離散程度的估計（方差、標準差）后，并沒有引入置信區間、置信系數等內容來說明怎樣對“樣本估計總體”的可接受性做出判斷.只是指出：由于樣本選取具有隨機性，用樣本的頻率分布、平均數和標準差去估計總體的分布、平均數和標準差，可能會存在一定誤差，但這一誤差一般不會影響對總體分布情況的大致了解.盡管教材也指出了當樣本代表性不好時，很可能對總體做出錯誤的估計，但是這個“可能性”是多少，怎樣刻畫，并未深入討論.到這一步時，可以很自然的引入正態分布、極限定理（大數定律、中心極限定理）等內容.中國教材的這種編排破壞了數學知識的整體性.中國教材在必修第二冊中先介紹了抽樣方法，然后介紹用樣本估計總體，在這里可以深入介紹一些統計推斷的內容，卻沒有深入介紹，打亂了數學的邏輯順序.

3結論與啟示

3.1結論

通過對兩套高中數學教材“概率與統計”內容的比較研究，我們得出以下結論：

（1）在知識點數量上，中國教材多于日本教材.在知識廣度上，中國教材高于日本教材.

（2）兩套教材都是概率內容多于統計內容，中國教材概率知識點數量遠多于統計.其中，概率部分，兩套教材的內容基本一致;兩套教材關于描述性統計內容的知識點是一樣的，在統計部分，兩套教材差別較大，不過日本教材中沒有安排一元線性回歸的內容.

（3）從兩套教材對知識點的處理看，中國教材比較注重定義的嚴格性，注意結合具體案例引導學生參與數據分析的全過程.日本教材則比較注重數學知識內部的聯系，強調數學是一個整體.兩套教材都很強調統計知識的應用，注重培養學生的數學應用意識，也比較注重統計軟件在教學中的運用.

3.2啟示

（1） 教材的編寫應注意各數學分支之間的聯系

數學的各個分支是一個不可分割的有機整體，在作為整體的數學中，使用著相同的邏輯工具，存在著概念間的親緣關系.概率與統計也不是孤立存在的，尤其是隨著大數據時代的來到，其應用范圍也越來越廣.國際著名數學教育家弗賴登塔爾（H. Freudenthal，1905-1990）曾強調：“不要教孤立的片斷，要教連貫的材料，因為有聯系的事物學得快，記得牢.”從認知心理學的角度來看，學生掌握了一門學科的基本結構后，能夠幫助他理解相關知識，達到觸類旁通、融會貫通的境地.然而我們的教材的編寫常常將數學按模塊或領域劃分，將概率統計作為獨立的內容，這樣不利于學生形成一個整體的數學觀，導致學生會認為數學各個分支之間毫無聯系.兼顧歷史（數學的發展歷程）、邏輯（數學科學的特征）、心理順序（學生認知結構）和學生已有知識經驗的教材才是理想的教材.將它們作為一個整體進行講授，可以幫助學生形成“數學的各個分支是一個整體”的觀念，同時算術、代數、幾何等內容可以促進學生對“概率與統計”知識的理解.比如蒲豐投針試驗，這是將概率與幾何聯系在一起的一個非常好的實例.再如著名的蒙特卡洛方法，我們可以通過這一方法來計算幾何中許多不規則圖形的面積.而將搜集的數據，通過點圖（dot diagram）、莖葉圖（stem and leaf diagram）、箱線圖（box and whisker plot）、直方圖（histogram）等直觀的表示出來，讓學生經歷數據處理的全過程.在親自參與的過程中學習數據分析的方法，并運用統計結果解釋實際問題.

現實的數學不僅僅是各數學分支之間的相互交織，還應聯系著物理、化學、生物等自然科學和一些人文學科.這些學科中許多內容都可作為概率統計教學的素材，教材中也舉了相關例子來說明數學在其它學科以及生活中的應用，但與“標準”的要求還有不小差距.

（2）教材應引入統計軟件來輔助教學

有學者指出，中小學的概率統計教學應該是一種直觀的教學＼[13＼].《標準》中也建議：“鼓勵學生盡可能運用計算器、計算機進行模擬活動，利用計算機輔助更好地體會概率的意義和統計思想.”＼[1＼]

日本教材中專門用一節來介紹怎樣利用統計軟件計算一些描述性統計量，如均值、眾數、中位數、極差、方差標準差以及相關系數的計算.中國教材在隨機抽樣部分，簡單介紹了用Excel和R軟件來產生隨機數.而后以“信息技術應用”的形式介紹了Excel和R軟件的簡單統計功能.在選擇性必修3中，以“信息技術應用”的形式介紹了GeoGebra的簡單應用.中日兩國的高中數學課程標準中，都明確提出要將現代信息技術融入數學教學，讓計算機成為學生數學學習的有力工具.但從教材中概率與統計的內容來看，計算機的融入做得還不盡如人意.

利用計算機對數據進行處理，是對學生計算能力培養的重要組成部分.在概率統計的教學過程中，計算機的使用是很有用處的，是學生學習和教師教學的重要輔助手段，為師生交流、生生交流、人機交流搭建了平臺，為學習和教學提供了豐富的資源.除了作為計算工具，更重要的是利用計算機和數學課程深度融合，實現傳統教學手段難以達到的效果.如何在保持傳統數學教學優勢的基礎上，將計算機融入教學，在“依賴”與“運用”之間達到平衡，是一個值得深入研究的課題.

參考文獻

[1]教育部.普通高中數學課程標準（2017年版2020年修訂）＼[M＼].北京：人民教育出版社，2020：90.

[2]覃淋.美國現代數學教育改革及其啟示＼[J＼].中學數學研究，2018（6）：14.

[3]李勇，章建躍.全國重點高中數學教師概率統計知識儲備現狀調查＼[J＼].數學通報，2016，55（9）：19.

[4]課程教材研究所.普通高中教科書A版 數學：必修第二冊＼[M＼].北京：人民教育出版社，2020：172260.

[5]課程教材研究所.普通高中教科書A版 數學：選擇性必修第三冊＼[M＼].北京：人民教育出版社，2020：43136.

[6][日]大島利雄.改訂版 數學I [M].東京：數研出版株式會社，2021：134155.

[7][日]大島利雄.改訂版 數學A [M].東京：數研出版株式會社，2021：3050.

[8][日]大島利雄.改訂版 數學B[M].東京：數研出版株式會社，2021：100129.

[9]陳希孺.概率論與數理統計＼[M＼].合肥：中國科學技術大學出版社，2009：59.

[10]C.R.勞.統計與真理：怎樣運用偶然性＼[M＼].北京：科學出版社，2004：104-118.

[11]袁智強.數學師范生整合技術的學科教學知識發展研究＼[M＼].北京：科學出版社，2016：41.

[12]A.D.亞歷山大洛夫.數學——它的內容、方法和意義（第一卷）＼[M＼].北京：科學出版社，2019：1.

[13]覃淋.大陸和臺灣高中數學教材“統計與概率”內容比較研究＼[J＼].中學數學雜志，2017（09）：2023.

作者簡介覃淋（1991—），男，四川南充人，碩士，助教;主要研究數學史與數學教育;發表論文10余篇，其中人大復印報刊資料《高中數學教與學》全文轉載3篇.

喻曉婷（1993—），女，四川巴中人，助教;主要研究中小學數學教育教學.

張靜（1992—），男，四川廣安人，小教二級教師;主要研究小學數學教育教學.