基于PISA2021分析高考情境題的數學推理能力

俞卓君 周瑩 陳基河

【摘要】本文以PISA2021數學推理與問題解決為框架，從情境、內容、素養、過程四個維度，結合部分高考情境試題說明數學推理的具體體現，以期為教師教學提供參考.研究結果表明近幾年高考數學卷情境化試題背景在函數、幾何、概率等主線都有所體現，并貫穿于六大核心素養中.為了更好地培養學生的數學推理能力，在教學中可以注重對解釋部分的評價，同時加強數學抽象與數學建模素養的培養，情境試題的素材選取更多貼近生活實際.

【關鍵詞】PISA2021;數學推理;問題解決;高考情境試題

1問題提出

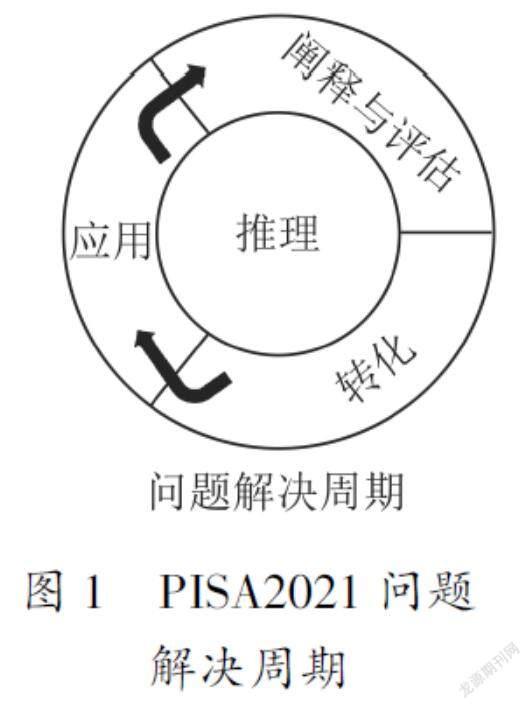
PISA是一項跨國跨文化的指向學生素養評估的大規模測試，無論是試題還是測評結果都對教育評價有著重要的研究意義.PISA2021測評框架與前幾個版本的區別是重點強調了數學推理能力在問題解決過程中的體現＼[1＼]，如圖1.

PISA測試與中國的數學高考測試內容完全不同，但都希望能在檢測過程中反映社會需求＼[2＼].高速發展的21世紀對培養多樣化高素質人才、發展高階思維的需求愈加緊迫，＼[34＼]問題解決成為發展高階思維、培養21世紀技能的重要途徑.許多國家都把發展學生的數學推理能力放在問題解決過程中培養，并成為了重要的教學目標之一.推理能力在問題信息的提取、篩選和整理過程中起著至關重要的作用，更是幫助作出恰當判斷和決策的重要思維能力＼[5＼].

PISA2021強調將對數學推理的理解置于現實世界的真實情境，數學情境問題解決需要學生多種核心素養在情境中共同作用，是一種較高水平的數學素養.＼[67＼]李娜等學者分析了PISA2021測試框架，提出可以結合具體的數學內容來說明數學推理的具體體現＼[1＼].PISA2021給出了理解數學推理的六個關鍵：理解數量、數系及其代數性質;感知抽象和符號表征的力量;意識數學結構和它們的規則;認識數量之間的函數關系;借助數學模型作為觀察現實世界的鏡頭;理解方差是統計的核心＼[8＼].

為了深入探究數學推理在情境試題中的實際應用，本文參考PISA2021數學素養重點關注的數學推理能力與問題解決相互聯系的框架，以近年來部分高考數學情境類試題為研究對象，將抽象的推理能力具體化，期望能夠為數學問題解決過程中培養學生的數學推理能力提供參考.

2分析維度

本文分別從情境維度、考察的內容維度、情境中的素養維度以及問題解決的過程維度來分析高考試題中體現出來的數學推理能力，由于PISA2021中提出了理解數學推理能力的六個關鍵點，因此本文分析的高考樣題分別根據六個關鍵點進行選取.

2.1情境維度

本文主要關注高考試題中的4類情境：一是個人情境，個人情境與個人生活息息相關，包括旅行、購物等;二是社會情境，社會情境與學生身邊環境相關，比如人口數量、經濟政策等;三是職業情境，職業情境大多涉及財務成本、質量控制等;四是科學情境，包括氣象、醫藥、遺傳、環境等.

2.2內容維度

PISA2021的數學素養框架中將數學內容分成了四類：數量、不確定性與數據、變化與關系、空間與圖形.由于分析樣題來自于高考試題，因此本文選取的內容維度以課程標準為依據，結合高中數學三大主線：函數、幾何、概率與統計進行闡述.

2.3情境中的核心素養維度

《普通高中數學課程標準（2017年版）》提出了6種數學核心素養：數學抽象、直觀想象、數學建模、邏輯推理、數學運算、數據分析.每一道情境問題的解決都涉及多個核心素養，這也是數學推理能力在多素養中的體現.

2.4問題解決的過程維度

PISA2021將數學推理能力在問題解決的過程分成三方面：數學推理的表達、數學推理的應用、數學推理的解釋＼[8＼].學生在“表達”過程中提取問題的關鍵信息，在“應用”過程中解決問題，在“解釋”部分能結合實際闡述答案與結論.三個過程具體包括的活動如表1所示[1].

3試題分析

3.1理解數量、數系及其代數性質

在高中階段，學生需要掌握幾種重要的運算對象：數、字母（代數式）、向量等＼[11＼].數字是數學的中心概念，學生對情境問題進行數學推理的前提是能夠正確理解數字體系及對應的數量關系.中學數學包括多種數字表示形式，這需要學生能夠在多種形式之間進行轉化，如建立簡單代數等式、繪制圖形、建模，并在數字的轉化應用中進行運算.

例1（2019年全國卷理科17題）

為了解甲、乙兩種離子在小鼠體內的殘留程度，進行如下試驗：將200只小鼠隨機分成A，B兩組，每組100只，其中A組小鼠給服甲離子溶液，B組小鼠給服乙離子溶液.每只小鼠給服的溶液體積相同、摩爾濃度相同.經過一段時間后用某種科學方法測算出殘留在小鼠體內離子的百分比.根據試驗數據分別得到如下直方圖：

記C為事件：“乙離子殘留在體內的百分比不低于5.5”，根據直方圖得到P（C）的估計值為0.70.

（Ⅰ）求乙離子殘留百分比直方圖中a，b的值;

（Ⅱ）分別估計甲、乙離子殘留百分比的平均值（同一組中的數據用該組區間的中點值為代表）.

本題情境為科學情境（小白鼠醫學實驗），在醫學實驗運用科學技術手段進行藥物檢測的過程中，常常通過對小白鼠的試驗數據來分析檢測某種藥物的含量、有效性等關鍵信息.在內容維度上，本題主要考查頻率分布直方圖及概率的運算.主要考查了數學運算和數據分析的核心素養.學生通過概率估計值與事件C描述的運算過程，感悟其中蘊含的邏輯推理.

數學推理的過程體現在：要求確定數學變量“事件估計值”和“平均值”在直方圖中的含義，能夠識別問題隱含的數學關系，根據P（C）的估計值列出對應關系式.在應用中要能夠進行基本的數學運算，根據運算結果得到數學結論.本題要求學生解釋直方圖中呈現的信息，這一部分的解釋體現在學生的思維中，求出甲乙各自的平均值后，學生能夠根據均值的含義認識兩種溶液的集中趨勢.

3.2感知抽象和符號表征的力量

數學是一門研究數量關系與空間形式的學科，具有高度的抽象性和形式化的特點.在中學數學中，抽象是從問題情境中提取具體對象、運用符號表征進行數學運算等思維活動的過程.

例2（2021年上海卷19題）

已知某企業2021年第一季度的營業額為1.1億元，以后每個季度的營業額比上個季度增加0.05億元，該企業第一季度的利潤為0.16億元，以后每季度比前一季度增長4%.

（1）求2021年起前20季度營業額的總和;

（2）請問哪一季度的利潤首次超過該季度營業額的18%？

本題情境屬于社會情境（企業利潤變動），企業的營業額與利潤分析能夠反映該企業的經營狀況，從而幫助財務部門根據分析結果對未來的營銷決策做出預測.在內容上，這道題主要考查函數的單調性，運用數學抽象與邏輯推理使用函數解決問題.過程中涉及符號語言和文字語言，文字語言用于描述情境問題，符號語言用于表征數學概念和原理.數學推理的過程體現在：學生應該使用合適的變量、符號來數學化地描述問題情境.在本題中，文字語言為：首次超過該季度營業額的18%，符號語言為：0.16×（1+4%）n>（1.1+0.05n）×18%.在題中要創建恰當的數學解決策略，如第一問要求學生能構建以1.1為首項，0.05為公差的等差數列.在解釋上，有了計算結果則可根據提問說明對應的實際結論.

3.3意識數學結構和它們的規則

數學結構是各種數學對象的統稱，在解題中往往起著支撐作用，解題者可以通過對結構的感知、識別、聯想、歸納、類比、轉化等方式實現解題目標＼[13＼].在數學結構觀下，對結構的另一種重要的處理方式是合情推理＼[14＼]，學生首先認識到問題情境的結構，判斷關鍵的結構要素，通過歸納類比的方式了解結構，再將結構應用到問題情境中.

例3（2019年理科全國卷Ⅱ16題）

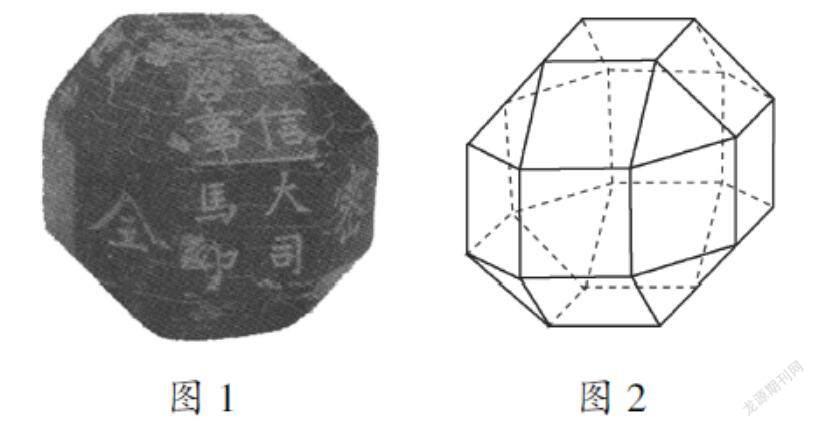
中國有悠久的金石文化，印信是金石文化的代表之一.印信的形狀多為長方體、正方體或圓柱體，但南北朝時期的官員獨孤信的印信形狀是“半正多面體”（圖1）.半正多面體是由兩種或兩種以上的正多邊形圍成的多面體.半正多面體體現了數學的對稱美.圖2是一個棱數為48的半正多面體，它的所有頂點都在同一個正方體的表面上，且此正方體的棱長為1.則該半正多面體共有個面，其棱長為.

本題情境為科學情境（中國金石文化），以中國文化為載體，以半正多面體為對象，主要考查正方體的結構以及棱長的概念，考查了直觀想象和數學抽象的核心素養.本題借助學生已有認知結構中的空間幾何體模型作為認識世界的工具，對于不認識的幾何體，能否通過觀察它的特殊結構并聯想到已經學過的知識，得到未知事物的特性. 數學推理的過程體現在：學生要能夠使用合適的圖形來數學化地呈現情境問題.金石是一種不規則形狀，但根據題目提示可將其抽象在正方體中.將圖2與正方體的結構搭建聯系，這一步有助于學生能夠準確認識兩者的形態位置，有了對圖2更加立體的觀察、比較，才能夠推斷并分析出二者棱長的位置關系.根據抽象出來的圖，可以推導出半正多面體棱長x與正方體棱長1的關系式為： 22x+22x+x=1，抽象的過程即為解釋圖形信息的過程.

3.4認識數量之間的函數關系

變量之間相互依賴和相互作用會對問題情境產生影響，從而影響學生的數學推理能力.數量之間的函數關系蘊含在問題情境中，可以選擇多種方式對其表示，如方程式、圖表、表格或文字描述.學生解決問題除了關注題目中確定的量，也要考慮可變的量，以及變量之間的變化規律，比如具有某種線性關系的函數.

在問題解決中，函數有著雙重屬性，既可以作為過程，也可以作為對象.作為過程的函數在數學表征中是抽象的，要將其作為對象，需要學生通過數量關系將其具體化.

例4（2020年理科全國新高考卷6題）

基本再生數R0與世代間隔T是新冠肺炎的流行病學基本參數.基本再生數指一個感染者傳染的平均人數，世代間隔指相鄰兩代間傳染所需的平均時間.在新冠肺炎疫情初始階段，可以用指數模型：I（t）=ert描述累計感染病例數I（t）隨時間t（單位：天）的變化規律，指數增長率r與R0，T近似滿足R0=1+rT.有學者基于已有數據估計出R0=3.28，T=6.據此，在新冠肺炎疫情初始階段，累計感染病例數增加1倍需要的時間約為（ln2≈0.69）（）.

A.1.2天B.1.8天

C.2.5天D.3.5天

本題情境為科學情境（新冠肺炎疫情時間變化）.突如其來的新冠肺炎疫情在全球范圍內大流行，疫情的傳播程度和嚴重性令人深感擔憂的同時，各國醫藥專家通過計算機等科技手段對疫情的傳播速度和感染人數進行研究，在調取了大量現實數據的基礎上估計模型.在內容維度上，這道題主要考查指數函數模型的實際應用.指數函數是高中重要的基本函數模型之一，解答本題的關鍵步驟是能夠建立兩個時間——病例數增加前（t1）與增加后（t2）的兩個關系式.同時本題考查了數學運算和邏輯推理的核心素養.數學推理的過程體現在：對于抽象的數學表述，學生也可以借助指數函數的圖象表征形式來翻譯時間變化的過程，通過圖象更直觀、立體地感受該模型變化的動態性和過程性.本題建立在疫情大數據的背景下，學生要能夠處理數據信息、代數表達式I（t）=ert，并根據問題建立方程.

3.5借助數學模型作為觀察現實世界的鏡頭

模型是對現實的簡化，數學模型可以使學生將學習的數學知識與現實世界存在的問題情境建立科學聯系.數學模型是用數學語言來表述的，以圖象或者函數關系式的形式，突出某一情境中的某些因素.

在一般情況下使用數學模型，通常能夠進行數據的分析和評估（模型是否適合數據），對未來做出預測，得到研究結果，并根據結果評估模型的充分性和準確性.在模型的建立與使用中引導學生關注情境中最重要的元素，將復雜的問題歸結為某種數學本質，進而幫助學生利用模型進行數學推理.

例5（2021年北京卷8題）

對24小時內降水在平地上的積水厚度（mm）進行如下定義：

小明用一個圓錐形容器接了24小時的雨水，如圖3，則這一天的降水量屬于哪個等級（）.

A.小雨B.中雨C.大雨D.暴雨

本題情境為科學情境（氣象預測模擬），在地理氣象預測中，常常利用數學和信息技術對天氣現象進行模擬分析以及預測，傳統氣象站的雨量器一般為圓筒，圖3筒內含兩節裝置，上節為漏斗，下節為儲水瓶.在內容維度上，這道題主要考查幾何主線中圓錐體積的計算，考查了數學抽象、數學建模的核心素養.該問題的核心是圓錐體積V與厚度h（mm）之間的關系.數學推理的過程體現在：要求學生能夠識別雨量器（圓錐體）是情境中模擬的數學模型，該模型對現實的氣象預測進行了簡化，學生要轉換不同的數學語言對模型進行描述，從圖象到數字再到文字，從而幫助做出預測.選擇題的題型對學生的數學結果準確性要求較高，不僅要求學生能夠創建合適的計算策略，也要求學生能夠根據運算答案以及表格對應的信息得到對應結果，從而能夠判斷這種方法在實際生活中的合理性.

3.6理解方差是統計的核心

現實生活充滿著不確定性，這種不確定性在21世紀的大數據背景下顯得尤為突出，在統計學中，方差可以刻畫隨機變量的離散程度，我們需要認識到數據具有的偏離程度，對離散程度進行描述，進而對現實情境進行判斷.

例6（2021年全國卷文科數學乙卷17題）

某廠研制了一種生產高精產品的設備，為檢驗新設備生產產品的某項指標有無提高，用一臺舊設備和一臺新設備各生產了 10 件產品，得到各件產品該項指標數據如下：

舊設備和新設備生產產品的該項指標的樣本平均數分別記為和，樣本方差分別記為 s21和 s22.

（1） 求， ，s21，s22;

（2）判斷新設備生產產品的該項指標的均值較舊設備是否有顯著提高 （如果-≥2s21+s222 ，則認為新設備生產產品的該項指標的均值較舊設備有顯著提高，否則不認為有顯著提高）.

本題情境為社會情境（設備質量控制）.隨著機器使用時間加長，陳舊會帶來精度下降，但是否使用新設備，何時使用新設備也影響著工廠的成本，因此在實際生活中，通過新舊設備的測試指標進行統計，能夠幫助工廠做出決策.在內容維度上，這道題主要考查均值與方差公式的計算，重點考查了數學運算與數據分析的核心素養.在高中階段，數據分析的一個重要過程是整理數據，整理數據是有效進行數據分析的基礎.數學推理的過程體現在：本題直接考查均值與方差的概念，要求學生能夠寫出計算，，s21，s22的步驟.學生應能夠進行簡單的數據運算，能根據題目條件判斷計算結果.

4結論與思考

通過對近幾年高考部分情境試題數學推理能力體現的分析可以看出，數學推理不僅僅存在于某個知識板塊，而是囊括了函數、幾何、概率多個板塊.

在對情境問題進行數學抽象的過程中，為了將最終的結果指向數學問題的解決，需要以符號語言為工具進行推理.直觀強調可視化，想象則需要根據學生的個體數學經驗對直觀圖形進行判斷，用數學語言描述直觀想象的結構過程中體現數學推理能力.數學建模的目的是促進現實世界與數學知識的聯系，幫助對現實問題做出合理推斷和估計.數學運算屬于數學中程序性知識的范疇，程序性知識需要按照規則與邏輯關系進行學習，因而在數學運算中能夠潛移默化地滲透數學推理能力.學生在真實情境中進行數據分析時，不僅要在收集數據時需要根據某些條件判斷數據的合理性與真實性，也要運用統計方法對數據蘊含的信息進行整理推斷，在數據的認識與分析過程中發展數學推理能力.

基于研究結論，本文提出幾點建議：

4.1課堂教學關注對數學推理的解釋與評價

數學推理在問題解決中的過程包括表達、應用與解釋，對數學推理的解釋與評價要求學生能夠結合問題的實際生活背景來闡述數學答案及其意義，這一過程鮮少能夠體現在考試答卷上.因此在日常教學過程中，可以結合PISA 2021所給出的數學解釋的具體信息（表1），幫助學生對問題解決中的數學推理進行歸納總結，解釋推理不僅能培養創造性思維，也能使學生在問題解決中經歷的過程更加完整.

4.2加強數學建模與數學抽象能力

數學推理能力與核心素養緊密關聯，在現實情境中，數學抽象與數學建模對發展數學推理能力尤為重要.數學建模是用數學概念、原理和思維方法描述現實世界中具有數學規律性的事件.問題情境與數學建模和數學抽象息息相關，情境常常通過文字或者圖形語言的模型來描述，提高抽象與建模的數學能力有助于學生在情境問題中發展數學推理能力.

4.3試題情境與時俱進，緊密聯系生活實際.

PISA對于數學素養的測評試題往往來自真實情境，強調學生對具體的問題情境做出數學分析、推斷和數學解釋.數學問題情境種類繁多，涉及面廣，或貼近生活或與大環境相關.例如在2020年新冠肺炎全球蔓延的環境下，學生親歷疫情人數暴增的階段，也常通過新聞媒體報道感染病例數與治愈人數等真實事件來感受疫情數據的變化情況.學生雖然不能直接參與醫學專家研制藥品、制定模型等事件，但在未來職業中可能會從事相關實際問題.在設置真實情境中的數學問題時，需要考慮真實情境的語言描述，對數據進行取舍，考慮學生的認知水平.

參考文獻

[1]李娜，趙京波，曹一鳴. 基于PISA2021數學素養的數學推理與問題解決＼[J＼]. 課程·教材·教法，2020，040（004）：131137.

[2]任子朝，佟威，陳昂.高考數學與PISA數學考試目標與考查效果對比研究＼[J＼].全球教育展望，2014，43（04）：3844.

[3]周瑩，莫倩華，肖寶瑩.美國大學招錄標準評介及啟示＼[J＼].數學教育學報，2019，28（06）：4246.

[4]周瑩，林毅.初中生數學高階思維的結構模型建構及問卷編制＼[J＼].數學通報，2021，60（02）：1624.

[5]吳宏.推理能力表現：要素、水平與評價指標＼[J＼].教育研究與實驗，2014（01）：4751.

[6]熊露，趙思林，程雪蓮. 情境視角下2019年高考數學試題評析及教學建議＼[J＼]. 教學月刊·中學版（教學參考），2019，000（012）：6165.

[7]鄧海英，嚴卿，魏亞楠.數學情境問題解決錯誤分析與評價＼[J＼].數學教育學報，2021，30（01）：6167.

[8]OECD. PISA 2021 mathematics framework（draft）＼[R＼]. Paris： OECD Publishing，2018：14.

[9]桑賈伊·馬漢賈恩＼[美＼]，茲比格涅夫·馬齊尼亞克波蘭，比爾·斯密特美，等. 2021年PISA數學——來自CCR的分析＼[J＼]. 數字教育，2019，005（005）：P.8392.

[10]史寧中. 試論數學推理過程的邏輯性——兼論什么是有邏輯的推理＼[J＼]. 數學教育學報，2016，025（004）：116，46.

[11]中華人民共和國教育部. 普通高中數學課程標準（2017年版）＼[M＼].北京：人民教育出版社，2018：47.

[12]譚業靜，平光宇. 基于數學文化和核心素養的符號語言教學＼[J＼]. 基礎教育論壇，2020（28）.

[13]張宏斌. 試述數學結構思想及其在數學教學中的運用＼[J＼]. 遼寧教育行政學院學報，2006（12）：125125.

[14]沈良. 略談數學結構觀下的解題與教學＼[J＼]. 數學通訊，2012（12）：13.

[15]胡典順，雷沛瑤，劉婷. 數學核心素養的測評：基于PISA測評框架與試題設計的視角＼[J＼]. 教育測量與評價，2018，213（10）：4147+65.

[16]史寧中. 漫談數學的基本思想＼[J＼]. 數學教育學報，2011.

作者簡介俞卓君（1996—），女，廣西南寧人，廣西師范大學數學與統計學院在讀碩士研究生;主要研究數學課程與教學論.

周瑩（1962—），女，浙江嵊州人，廣西師范大學數學與統計學院教授，碩士生導師，特拉華大學訪問學者;主要研究數學課程與教學論和教師教育.

陳基河（1996—），男，廣西玉林人，廣西師范大學數學與統計學院在讀碩士研究生;主要研究數學課程與教學論.