2021年高考概率與統計試題的統計與分析

胡茗潔 石浩楠 胡典順

【摘要】概率與統計是高中數學課程的主線，也是高考數學的主要考查內容.以2021年高考數學新高考Ⅰ卷、新高考Ⅱ卷、全國甲卷理科等八套試卷中“概率與統計”相關試題為研究對象，從情境類型、知識點、數學核心素養、關鍵能力、綜合難度五個維度對其進行特點分析.發現，2021年高考數學“概率與統計”試題具有情境類型豐富、講究知識的應用性與綜合性、融合多種核心素養與關鍵能力的特點，在難度上不同試題在難度因素的側重上各有不同，大部分試題強調運算難度.對教師的概率與統計教學和高考試題的命制提出以下幾點建議：豐富問題情境，培養關鍵能力;注重知識整合，建構完整體系;回歸知識本質，落實核心素養;合理設置難度，優化試卷質量.

【關鍵詞】高考數學;概率與統計;試題分析

1問題提出

隨著大數據時代的到來，概率與統計的基礎知識已經成為一個未來公民所必須具備的常識.在高中數學課程中，概率統計是一個重要主題，貫穿必修、選擇性必修和選修課程.解決概率與統計相關問題需要經歷問題情境的數學化、模型的建構、數據分析、數學運算、還原為現實問題的解等步驟[1]，是培養學生數學核心素養、發展應用意識的重要媒介.

近年來，高考對統計與概率的考查出現了新的趨勢：注重基本概念的理解與應用，試題情境更加真實和復雜，模型更加精細和完善[2].這不僅為教師的教學指明了方向，也對學生的學習提出了更多新的要求.故本文對2021年高考數學中的概率與統計試題進行分析，以期更清楚地把握高考的考核方向，為教師的教學提供思路，也為高考試題的命制提供參考.

2分析框架

本文以新高考Ⅰ卷、新高考Ⅱ卷、全國甲卷理科、全國乙卷理科、北京卷、上海卷、浙江卷、天津卷共八套試卷為研究對象，從情境類型、知識點、數學核心素養、關鍵能力、綜合難度五個維度出發對概率統計相關試題進行統計與剖析，并歸納得出2021年高考數學概率與統計試題的命制特點.在統計編碼過程中，統計結果經過與相關專家與團隊成員多次討論后確定，以盡可能保證統計的準確性與全面性.

2.1情境類型

概率是研究隨機現象的強有力工具，統計通過收集、分析數據解決實際生活中的問題，概率與統計已經滲透到現實生活的方方面面[3].基于概率與統計內容領域的特色，高考對此部分的考查一直堅持與情境相聯系，本文參考《普通高中數學課程標準（2017年版2020年修訂）》（以下簡稱“課標”）中對情境與問題的解釋，將情境劃分為現實情境、數學情境、科學情境三個維度.

2.2知識點

明晰考查內容領域的知識點，有利于教師和學生把握核心知識點，更好地應對高考的挑戰.本文參考課標中對知識點的劃分，選取其中“概率與統計”內容，結合試題實際情況，得到概率與統計的知識點編碼框架，具體內容見表1.

如表1所示，一級考點用字母表示，二級考點用數字表示.如，A2表示散點圖，B2表示回歸分析.試題中涉及的其他領域的知識點，由于不是主要內容，不做一一編碼，遇到時直接列出即可.

2.3數學核心素養

作為課標的一大亮點，數學核心素養滲透在幾乎所有的數學知識、技能中，是學生在接受教育過程中逐步形成的具備數學本質特征而且適應個人終身發展和社會發展需要的關鍵能力與思維品質[4].在概率統計的學習中，學生需要經歷數據統計的全過程，多種素養均能得到發展，本文參照課標中提出的六大數學核心素養——數學抽象、邏輯推理、數學建模、直觀想象、數學運算、數據分析[8]進行試題的統計與分析.

2.4關鍵能力

關鍵能力作為“一核四層四翼”中“四層”的一環，指學生在生活實踐中或探索問題情境時，應用知識有效地認識問題、分析問題、解決問題的能力[3]，是高中數學課程的培養目標.高考數學通過情境承載考查內容，以實現考查要求，這與概率與統計特有的情境性不謀而合，因此，在概率與統計這一內容領域更容易培養學生的數學關鍵能力.本文依據高考評價體系將關鍵能力劃分為邏輯思維能力、運算求解能力、空間想象能力、數學建模能力、創新能力五個維度.

2.5綜合難度

試題難度是反映試題質量和測驗公平性的一項重要指標.目前已有不少學者展開了對高考試題難度的研究，并形成了一些比較成熟的框架.本文綜合武小鵬所搭建的綜合難度模型框架[3]，以及薛歡等在此基礎上提出的針對于概率與統計試題的綜合難度模型[4]，對試題進行綜合難度的分析，模型的具體因素及其等級如表2所示.

在表2中，利用di=∑jnijdijn計算各因素的難度系數di，其中i表示不同的因素，dij表示第i個因素中的第j個等級的權重（依據不同等級分別取1，2，3，…），nij表示這組題目中屬于第i個因素中的第j個等級的題目個數，n代表題目的總個數.因此整套試題的綜合難度系數就是各因素綜合難度系數的加權平均，設ki為各因素在整個試題中所占的權重系數，那么整套試題的綜合難度系數D=∑7i=1diki.關于權重系數的確定，參考武小鵬[6]研究中韓高考試題時提出的權重系數，即以“背景因素”權重為1.00作為參考標準，各因素所占權重依次為1.00，1.21，1.19，1.53，0.91，1.17，1.35.

3數據的統計與分析

根據分析框架，將所得結果分為兩個部分分析：一部分呈現試題的命制特點，包括情境類型、知識點、核心素養和關鍵能力的分析;另一部分呈現綜合難度系數的分析.

3.1試題命制特點分析

在進行統計分析時，根據題目的設問方式，將試題分為封閉型試題和開放型試題兩類，封閉型試題包括選擇題和填空題，開放型試題包括解答題.

（1）封閉型試題特點分析

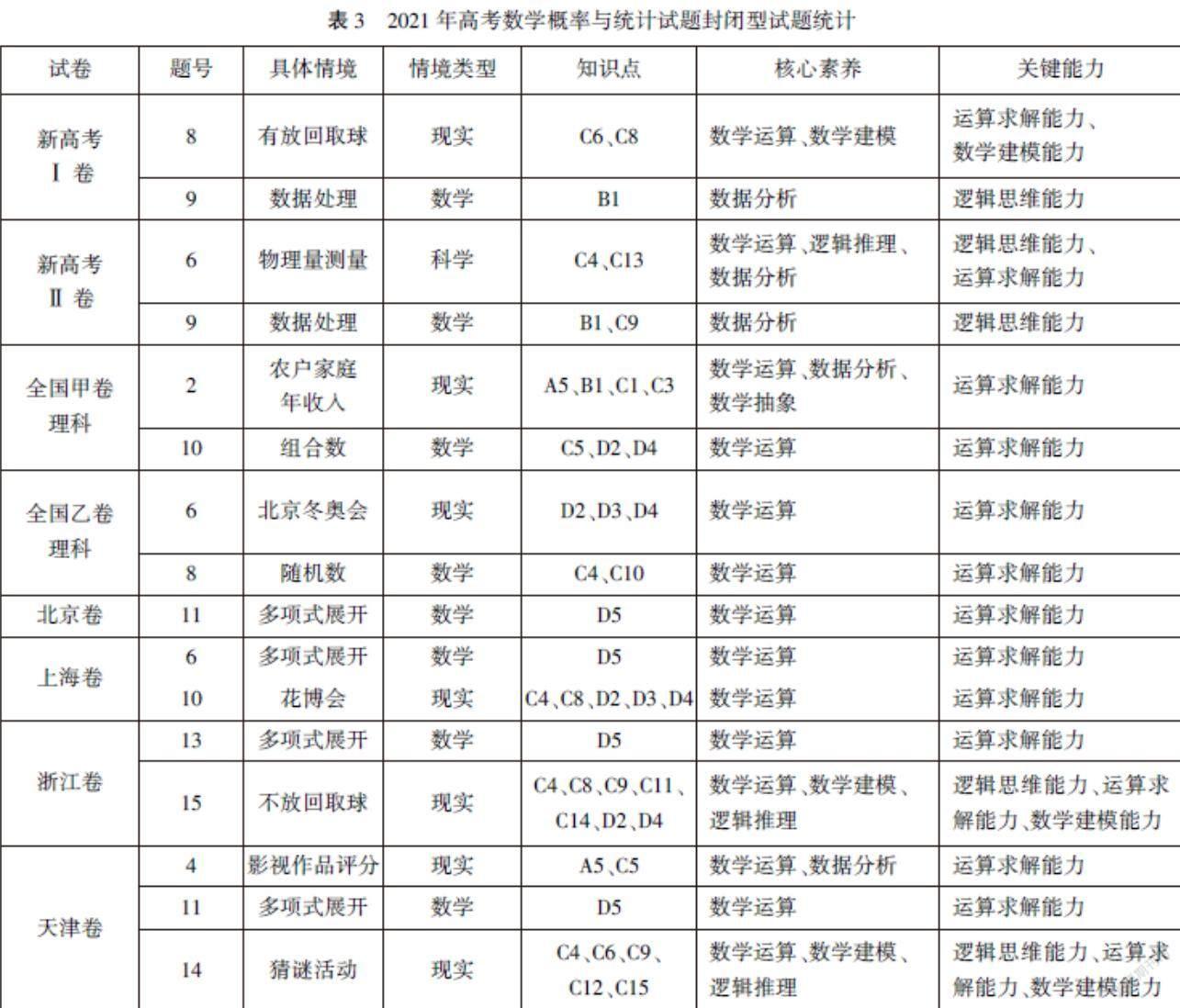
根據第二部分搭建的分析框架對2021年高考數學封閉型的概率與統計試題進行統計，具體內容如表3.

在情境類型方面，如圖1所示，考查情境類型多樣，以數學情境最多，現實情境次之，僅有新高考Ⅱ卷涉及科學情境的封閉型試題.從具體情境來看，高考充分體現了數學思政的要求，于問題情境中關注社會時事與經濟發展.如全國甲卷理科第2題[6]，“以我國在扶貧脫貧工作取得全面勝利和農村振興為背景，通過圖表給出某地農戶家庭收入情況的抽樣調查結果”，培養學生社會責任感，增強民族自豪感與國家意識.

在知識點的考查上，封閉型試題考查的知識點一般為1～3個，僅全國甲卷理科涉及4個知識點的封閉型試題.具體考查以概率為主干知識點，向外延伸，考查范圍廣，但與其他領域結合較少，符合概率與統計“廣而不深”的特點，講究知識的應用性與綜合性.

對于核心素養，在“重視理性思維，堅持素養導向、能力為重的命題原則”[7]下，核心素養以數學運算為主，在強調簡單運算的基礎上，落實數學建模、數據分析等素養的考查，表明高考數學命題順應時代特征，對概率與統計的實用性提出了要求，以便讓學生更好地應對現實生活中的問題.

對于關鍵能力的考核，以運算求解能力居多，但在兼顧概率與統計領域特點的同時，盡可能多地考查了其他能力，合理科學地踐行了高考評價體系，充分發揮了高考的選拔功能.

（2）開放型試題特點分析

根據第二部分搭建的分析框架對2021年高考數學開放型的概率與統計試題進行統計，具體內容如表4.

在情境類型方面，開放型試題的問題情境以現實情境為主，含有少量的科學情境.具體情境的選擇非常豐富，概括為如下三大特點：緊扣時事熱點，培養學生的家國情懷，如新冠肺炎檢測;貼近學生的日常生活，激發學生對數學學習的興趣，如“一帶一路”知識競賽;與科技、生產相融合，培養學生的數學應用意識，如微生物繁殖、機床生產以及研制新設備.

在知識點的考查上，開放型試題所考查的知識點通常有3～5個，普遍多于封閉型試題，體現出開放型試題的綜合性.大部分知識點歸屬于一級考點B和C之下，涉及其它領域數學知識的試題較少，僅有一題，幾套試卷相比較而言，新高考Ⅱ卷所考查的知識點是最多的，而且存在跨章節學科知識的交叉.

就核心素養而言，每道試題都考查了3～5種核心素養.根據每種核心素養所涉及的開放題數量，繪制雷達圖，如圖2所示.不難發現，概率與統計開放題側重邏輯推理和數學運算的考查.以新高考Ⅱ卷第21題為例，學生需要從微生物的繁殖情境中抽象出概率之間的數學關系，并在此基礎上建立模型進行期望的求解，最后通過邏輯推理加深對問題實際含義的理解.

對于關鍵能力，邏輯思維能力、運算求解能力、數學建模能力是大部分試題所涉及的，這與核心素養的考查相呼應.除此之外，少部分試題滲透了對于學生創新能力的培養，如全國乙卷第21題，重在考查學生思維的靈活性.

3.2試題綜合難度分析

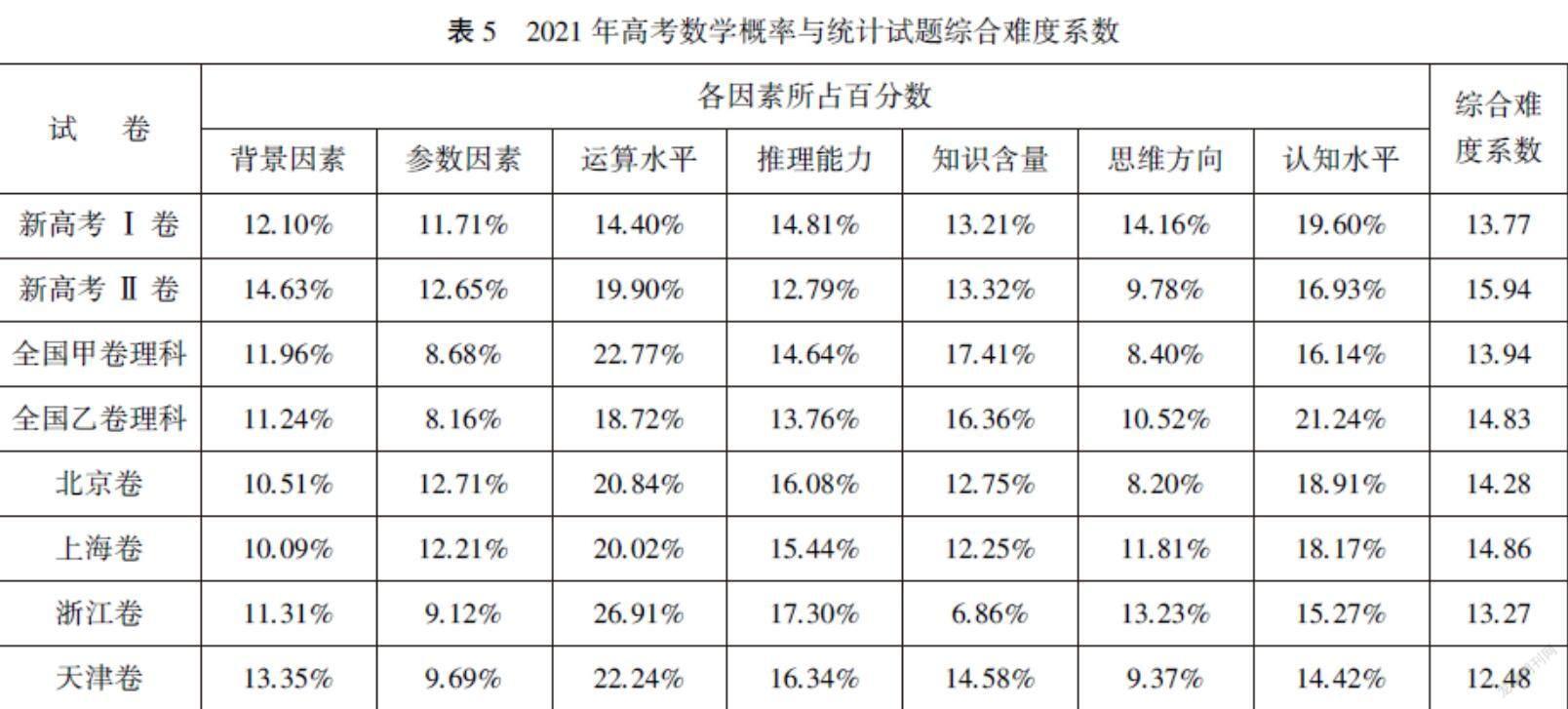
根據綜合難度模型下的公式，計算各套試卷概率與統計相關試題的綜合難度系數，如表5所示.

根據表5中的難度系數繪制折線圖，如圖3所示.

從宏觀整體來看，新高考Ⅱ卷的概率與統計試題綜合難度系數最高，天津卷的概率與統計試題綜合難度系數最低，其他幾套試卷概率與統計試題的綜合難度不相上下.從微觀細節來看，新高考Ⅰ卷認知水平因素貢獻難度最多，其他分配較均勻，全國甲卷理科知識含量與認知水平并重，新高考Ⅱ卷和全國乙卷理科則是運算水平與認知水平并重，北京卷、上海卷、浙江卷、天津卷對運算水平要求較高，或在參數因素或在思維方向因素占比較低，各有特色.

仔細剖析綜合難度系數的各難度因素，可以發現：在情境的選擇上，新高考Ⅱ卷最為綜合，具備一定的創新性;在運算水平上，浙江卷的要求最高，不少試題已經涉及到了符號運算，同時，浙江卷對推理能力的考查也是最復雜的;在知識點含量上，兩套全國卷的知識點含量是最豐富的;在思維方向上，新高考Ⅰ卷和浙江卷兩套試卷給予逆向思維更多的關注;對于試題所考查的認知水平，全國乙卷理科和新高考Ⅰ卷這兩套使用地區較多的試卷要求學生不僅掌握知識并應用，還要能夠進行一定的分析推理.

4啟示與建議

4.1豐富問題情境，培養關鍵能力

創設合適的問題情境，既能有效提高試題質量，也更有利于落實“一核四層四翼”的高考評價體系.概率與統計的廣泛應用性為高考試題中問題情境的創設提供了天然的優勢，2021年高考數學概率與統計相關試題的情境設置以現實情境居多，尤其是開放題，都非常貼近日常生活，聚焦時事熱點，突顯出理論聯系實際的導向.

在教學中，教師應注意情境創設的藝術，在教學中適當增加一些學生比較陌生的問題情境，為學生創新思維的培養提供探索的“黑箱”[8].在情境的設問方式上，要注意開放性，給予學生充分的思考空間，擺脫定勢思維的束縛，使學生得到關鍵能力的綜合發展.

4.2注重知識整合，建構完整體系

高考數學在考查過程中要體現綜合性，這樣有利于促進學生從整體上建構知識框架，形成合理的認知結構[9].概率與統計是高中數學知識點中的關鍵部分，與其他知識點有著明顯的滲透交匯，也是高考的重難點.2021年高考數學概率統計試題不僅涵蓋知識點豐富，而且已經有部分試題表現出函數、方程等跨章節甚至生物、科學等跨學科知識的交互，旨在培養學生融會貫通的意識.

在教學中，教師可以適當利用概念圖、思維導圖等知識表征工具幫學生梳理核心知識點，建構概率統計的知識體系.還應當及時地進行回顧復習，厘清概率統計與方程、函數、不等式等其它知識單元的聯系，深化對數學概念的理解.除此之外，教師還可以利用探究性學習的模式介紹一些學科交叉的內容，積極探索多學科交叉融合的有效途徑，以培養學生的創新意識.

4.3回歸知識本質，落實核心素養

對數學知識本質的理解是學生發展數學核心素養的必要條件，高考試題不僅要考查學生對知識點的熟練程度，更應當突出知識的本質，引導學生從學科的視角理解世界和分析問題，概率統計的本質是隨機性數學思維.今年高考數學中所涉及的古典概型、正態分布、幾何概型等隨機模型，皆是對現實隨機問題的抽象凝煉，既體現了數學之美，又彰顯了數學的實用性.

在教學中，教師應幫助學生轉變固有的思維方式，激發自覺培養隨機性數學思維的意識.在對典型題目進行剖析時，盡可能完整地展現推理過程，使學生積累一些常用模型，并且能靈活運用.通過對數學知識進行整體性的分析，梳理概率統計自身的邏輯關系，使得每一堂課都立足于概率統計的本質，聚焦其內核.

4.4合理設置難度，優化試卷質量

編制一套高質量的高考數學試題，最大的價值追求就是既要保證難度設計的科學合理又能檢測出學生的真實水平，同時還要充分發揮高考數學試題的選拔功能和積極導向作用.今年不同試卷概率與統計的試題在各難度因素的分配上各不相同. 但總體來說，試卷在難度的設計上均應當依據課標對概率統計部分的要求，秉持發展學生的數學核心素養理念，從每個難度因素自身的特點出發，合理設置各難度因素，提高試卷的區分度.

在教學中，教師應當把握概率與統計的教學重點，除了要求學生掌握知識點之外，更要培養學生的核心素養與關鍵能力，通過給予學生更多的具有現實背景意義的案例，讓學生體會數據分析的全過程，不斷提高運算水平，從概念理解逐步走向靈活運用、獨立分析.

參考文獻

[1]廖藝捷，朱展霖，胡典順.近五年高考概率與統計試題的統計與分析——以全國Ⅰ卷（理科）為例[J].數學通報，2021，60（02）：5662.

[2]趙軒，任子朝.高考概率統計試題考查目標的沿革與實現[J].數學通報，2019，58（10）：3943.

[3]中華人民共和國教育部.普通高中數學課程標準（2017年版2020年修訂）[M].北京：人民教育出版社，2018.

[4]路江江，王亞妮.高中數學教育中如何培養學生的數學核心素養——王尚志教授訪談錄[J].數學教育學報，2021，30（02）：6770.

[3]李勇，趙靜宇，史辰羲.高考評價體系的基本內涵與主要特征[J].中國考試，2019（12）：712.

[4]武小鵬，孔企平.基于AHP理論的數學高考試題綜合難度模型構建與應用[J].數學教育學報，2020，29（02）：2934.

[5][14]薛歡，杜劍南，路江江.2016—2020 年高考數學（理科）全國卷“統計與概率”試題探析——基于綜合難度模型[J].教育測量與評價，2020（12）：3040.

[6]武小鵬，張怡.中國和韓國高考數學試題綜合難度比較研究[J].數學教育學報，2018，27（03）：1924+29.

[7][10]教育部考試中心.聚焦核心素養考查關鍵能力——2021年高考數學全國卷試題評析[J].中國考試，2021（07）：7076.

[8]李健，童莉.高考評價體系中“應用性”與“創新性”要求——基于2020年高考數學試卷中問題情境的分析[J].基礎教育課程，2020（Z2）：1822.

[9]于涵，任子朝，陳昂，趙軒，李勇.新高考數學科考核目標與考查要求研究[J].課程·教材·教法，2018，38（06）：2126.

作者簡介胡茗潔（1998—），女，湖北宜昌人，華中師范大學數學與統計學學院研究生;研究方向數學課程與數學教學.

石浩楠（1999—），女，湖北十堰人，華中師范大學數學與統計學學院研究生;研究方向數學課程與數學教學.

胡典順（1965—），男，湖北孝感人，華中師范大學數學與統計學學院教授、博士生導師;研究方向數學課程與數學教學.