激光擴散片擴散角檢測系統設計及其誤差分析

張春鵬，白素平，閆鈺鋒，于信

（長春理工大學 光電工程學院，長春 130022）

激光擴散片是表面具有微凹透鏡結構的光束擴散器件，廣泛應用于激光照明、激光投影及激光掃描顯示等領域。到目前為止，有三種類型的擴散片：依賴于基材中加入的化學顆粒作為散射粒子的散射光擴散片；起混光作用但并不會真正將光擴散的衍射型擴散片；在基材表面設有微特征結構并進行陣列化，從而使光線透過時發生不同方向的折射，進而控制光的行徑路線，實現光束擴散的微結構擴散片［1］。激光擴散片屬于微結構擴散片的分支。

微結構光擴散片因其高透過率和易控制光束擴散角度、光場的空間及能量分布這兩種特性而受到高度重視。隨著微光學技術和微壓技術的發展，微結構擴散片的研究日益成熟，并發表了大量的研究文獻。任智斌，朱麗思等人［2］提出用光刻膠熱熔技術制備不同微結構的擴散片。莊孝磊，周芳等人［3］提出了一種新型的層疊微透鏡陣列光擴散片提高亮度增益。M.Yaegashi等人［4］提出基于材料極化選擇性來制作微結構的方法。楊雪，孫會來等人［5］總結了目前飛秒激光制備微結構的研究進展。在工藝完善的基礎上，何小祥，鄭秀婷等人［6］發現微結構長徑比對擴散片的光學性能有著重要影響并進一步研究。閆占軍，杜春雷等人［7］運用算法設計了隨機孔徑的微透鏡擴散屏設計。

盡管關于微結構擴散片的制備技術，光學特性已有諸多理論研究進展，但關于測量光束經擴散片擴散后的面光源的擴散角度還沒有特定方法。因此設計一套可以對激光擴散片擴散角進行自動化、高效率、高精度的檢測系統。用于對設計完成的擴散片擴散角進行檢測，起到質檢作用。并對影響測量精度的因素進行逐一分析，尋找最佳測試條件，進一步提高系統測量精度。

1 激光擴散片擴散原理及檢測系統

1.1 激光擴散片擴散原理

激光擴散片的原理圖如圖1所示，激光垂直入射到擴散片上，在微凹透鏡作用下，激光束發散出射，形成了有一定擴散角的面光源，擴散角度與擴散片上微凹透鏡參數有關。另外，從圖1中可以發現，在理想情況下，激光束經擴散片后的總體擴散角度與單一子透鏡的擴散角度是一致的。為了簡化分析出擴散角度與擴散片結構參數的關系，下面對子透鏡擴散過程單獨分析。如圖2是子透鏡的擴散示意圖，子透鏡有孔徑D，曲率半徑R這兩個參數，通過透鏡焦距公式，及幾何光學傳播定律得到方程組（1）。將方程組進行化簡整理就可以得到公式（2）。

圖1 擴散片原理圖

圖2 子透鏡擴散原理圖

其中，n是微凹透鏡材料折射率；f是微凹透鏡焦距。如果知道其他子透鏡的參數，就能夠將子透鏡的擴散角度求出，即得到激光擴散片的擴散角。由公式（2）還可發現擴散角θ正比于微透鏡孔徑D，反比于曲率半徑R。

擴散面光源實質是由每個微凹透鏡擴散后的小面光源疊加而成。為了確保面光源具有良好的均勻性，那么每個微透鏡所產生的面光源的擴散角的大小應該一致，所以要確保每個微透鏡的孔徑D與曲率半徑R的比值為常數。

微透鏡采用正三角形排布，可有效提高擴散片上微透鏡的填充率，從而提高擴散片透光率［8］，如圖3所示。此外，微透鏡填充率與微透鏡孔徑有關，微透鏡孔徑越小，填充率越高，一般要求微透鏡孔徑在10～100 μm范圍內。

圖3 微透鏡排布方式

對擴散片進行模擬分析，采用蒙特卡洛法建立數學模型［9-10］，得到了激光擴散片擴散角度和能量利用率。

蒙特卡洛法按照某種規律向系統中隨機投射大量光線，但不指定光線和系統內每個物體、表面相交的順序及相互位置關系。每條光線在它和物體的相交處可以被吸收、反射、折射、衍射或散射。光線在系統內的任意方向和空間傳播時，軟件會一直追蹤每條光線經過各種材料和表面后所攜帶的輻射通量發生的變化。輻照度分布的計算是把接收面劃分成矩形網格單元，把各網格單元內所有光線的輻射功率相加除以網格面積。真實系統產生的輻照度分布可以被看成是連續的，而非序列光學追跡法所得到的照度分布是離散的。理論上，根據采樣定理只要網格的密度大于目標面上照度變化空間頻率的兩倍即可完全再現照度分布的精確值。

采用蒙特卡洛法模擬的擴散片尺寸為40×40 mm，厚度1.2 mm，微透鏡孔徑D為40 μm，曲率半徑R為100 μm，材料選擇為介質折射率n=1.5的PMMA，在擴散片后100 mm處放置探測器，材料吸收特性忽略不計，模擬結果如圖4所示。

圖 4（a）、圖 4（b）為激光擴散前后照度分布圖，圖4（c）為子午截面上擴散前后照度分布曲線對比圖。從圖4（c）可發現激光光束經擴散片擴散后所得面光源能量分布雖然仍是中心強邊緣弱，但與未擴散的激光相比，其照度分布曲線更加均勻。另外，可根據探測器上獲得的總功率求得能量利用率高達88.73%，還可通過探測器X軸零點位置坐標求出擴散角度θ為11.31°與公式（2）計算結果相一致。

圖4 激光擴散前后照度圖

1.2 擴散角檢測系統

1.2.1 擴散角檢測原理

因為面光源邊緣處能量較弱，不宜測量，所以采用限制邊界條件的辦法，不是對面光源整體的擴散角度進行測量，而對面光源中心位置光強分布較為均勻處進行檢測。所以重新定義擴散角，系統要檢測的擴散角為面光源中心光強點與光強度為中心點60%的點之間的夾角。如圖5所示，α為所要檢測擴散角。

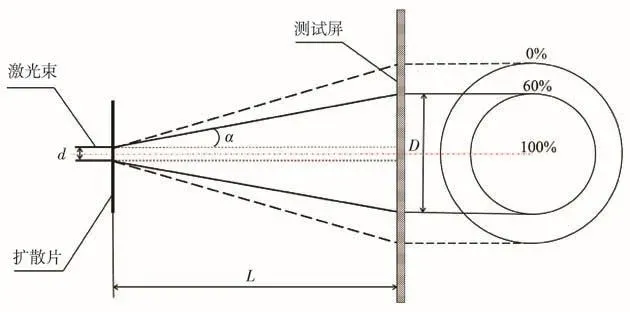
圖5 擴散角檢測原理圖

其中，d為激光束直徑；L為擴散距離；D為面光源徑向方向上的兩個60%強度點的距離。根據幾何定律可以得到擴散角α的角度：

在測試屏面光源豎直徑向方向上安裝高精度探測器進行脈沖位移，對所得照度值進行實時傳輸，找到強度最大點及兩個60%強度點，記錄D，且L和d均為已知，帶入公式（3）即可求得所要擴散角α。擴散角α與D和L有直接關系，而D又與脈沖步數相關，所以擴散角α與脈沖位移又有間接關系。

1.2.2 檢測系統工作流程

圖6為檢測系統工作流程圖。整個檢測系統由光束擴散系統、光束接收系統及系統控制端三部分組成。光束擴散系統中，激光束發出平行光源垂直入射到光束擴散系統上固定好的擴散片，激光束經擴散片上微透鏡作用下以一定擴散角度出射到光束接收系統上，光束接收系統上的高精度光電探測器與面光源中心對準，并對接收到的光信號進行由光信號到電流、電流到放大電壓、再到數字信號的一系列信號轉換，最終將數字信號傳入系統控制端的芯片中。芯片會對輸入的數字信號進行運算處理，得到目標值，即60%強度點的數值，并控制伺服電機運轉光束接收系統中的機械滑軌，高精度光電探測器隨機械滑軌向面光源邊緣移動，對接收到的信號進行實時傳輸，當達到目標值時停止。芯片通過電機跳轉步數計算得到兩目標值之間的距離即D，并進行最終計算得到擴散角度，直接顯示在控制端的顯示液晶屏上。

圖6 擴散角檢測系統工作流程圖

2 實驗及數據分析

對檢測系統進行搭建，由于外部光照對照度計光電探測器有著極大影響，為保證測量準確性需在暗室中進行測量。初始測量條件：L為1 m，光電探測器脈沖位移0.5 mm，即采樣間隔，將5次測量結果與5次模擬結果進行比對得到曲線如圖7所示。

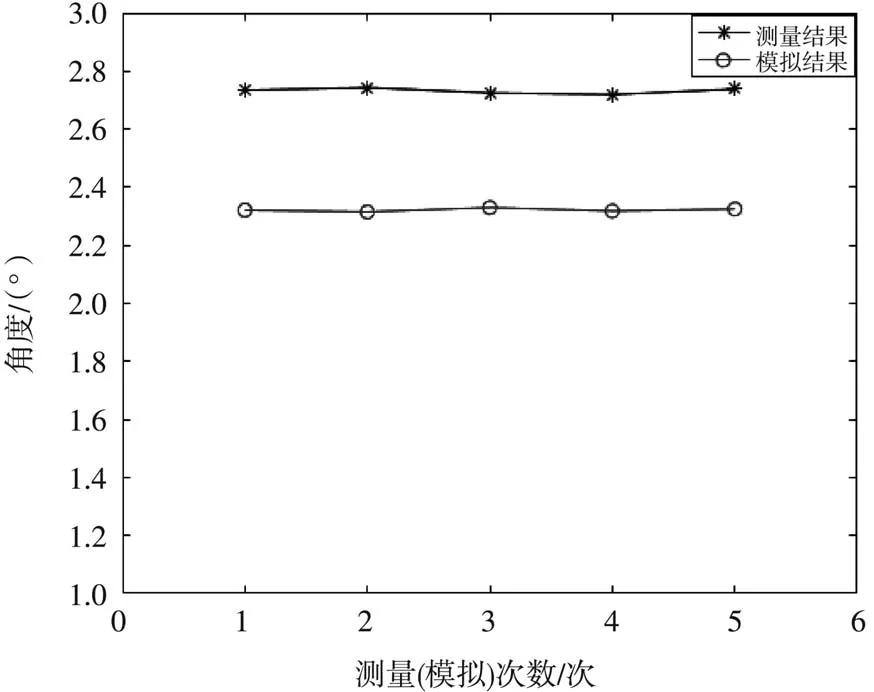
圖7 測量結果與模擬結果

根據圖7可知，測得擴散角遠大于實際擴散角（取5次模擬擴散角的結果均值為2.32°），這是因為探測器中IV轉換板增益倍率為定值，距離越近能量越高，造成中心點能量測量飽和，導致測量結果大于真實結果，增大測量距離，可有效提高測量精度。

為找到最佳測量距離L，固定采樣間隔0.5 mm，改變測量距離L，在1～2.5 m范圍內每隔0.1 m對擴散角為2.32°的擴散片進行測量，并將測量結果整合，如圖8所示。

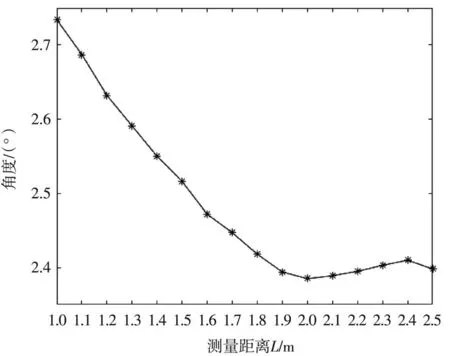
圖8 不同測量距離的測量結果

從圖8可發現在測量距離L為1～2 m時，測量結果持續減小，測量精度不斷提高，在2 m處測量結果為2.385°，2～2.5 m測量結果趨向穩定，故系統最佳測量距離為2 m。

還可發現，2 m處測量結果仍然微大于擴散角的實際值2.32°。這可能是采樣間隔過大引起，步進電機控制光電探測器在機械滑軌上進行每步0.5 mm的脈沖移動，在靠近60%強度點時，電機下一次跳轉，探測器移動0.5 mm，越過準確60%強度位置，造成D測量偏大，使得測量結果偏大。

為進一步提高系統測量精度。保持最佳測量距離2 m不變，改變采樣間隔，在0.1～0.5 mm范圍內每隔0.1 mm對擴散角為2.32°的擴散片進行測量，并將測量結果整合，如圖9所示。

圖9 不同采樣間隔的測量結果

由圖9可知，隨著采樣間隔的不斷減小，測量精度不斷提高，在采樣間隔為0.1～0.3 mm時，測量結果趨于穩定且相差不大，考慮到隨著擴散角度的增大，測量時長成幾何倍數增長，并且精度相差不大，為滿足在大擴散角擴散片（7.85°）測量時，節約時間成本，采樣間隔選為0.3 mm。

根據前面的實驗結果，得到最佳的測量條件為測量距離2 m，采樣間隔0.3 mm。下面對不同擴散角度的擴散片進行測量并記錄實驗數據，實驗結果如表1所示。

以上實驗過程均在暗室中進行，從表1可以看出，在最佳測試條件下，測量距離2 m、采樣間隔0.3 mm時，測量精度可達0.02°，最大時長小于3 min。

表1 不同擴散角擴散片測量結果

3 結論

本文根據現代工業檢測精度高，速度快的要求，建立了激光擴散片擴散角檢測系統，并介紹了擴散片工作原理和檢測系統的構成和工作原理。接下來，通過改變檢測條件測量距離L和采樣間隔，找到系統最佳工作條件為測量距離為2 m、采樣間隔為0.3 mm，以達到提高測量精度的要求。最后對不同擴散角的擴散片進行測量，實驗結果表明：在最佳測試條件下，測量精度可達0.02°，最大時長小于3 min。基本滿足了激光擴散片擴散角檢測的要求。