基于混合分布時間序列的K-GRU建模

吳維芝，施三支

（長春理工大學 數學與統計學院，長春 130022）

在實際生活中，無時無刻不在產生具有混合分布的時間序列數據。這些數據通常具有復雜的特性，如非平穩性和周期性等，還包含大量的隱含信息和一定的變化規律。因此，挖掘和分析混合分布時間序列中的有效信息，對日常生活和生產活動等具有十分重大的意義。

處理該類時間序列數據問題的方法多種多樣，如Zhangyulai等人［1］提出了一種新的非平穩時間序列建模優化算法，該算法采用移動窗口和指數衰減權值來消除歷史梯度的影響，能夠保證算法的收斂性。楊楠等人［2］采用混合高斯分布對時間序列數據進行建模，得到的模型具有較高的精度和泛化性能。Grunwald等人［3］使用馬爾科夫鏈建立和估計混合分布變量時間序列。Guo等人［4］提出了一種低維中期混沌時間序列預測的延遲參數化方法，具有較高的預測效果。闞子良等人［5］基于優化機器學習使用遺傳算法優化參數，對股價時間序列數據進行預測，該方法預測精度高且泛化能力好、魯棒性強。Shao等人［6］提出了LSTM神經網絡對具有非平穩性的街邊停車位占用率數據進行預測，該方法優于現有的預測方法。谷麗瓊等人［7］提出了基于Attention機制的GRU神經網絡并應用于非線性波動的股票數據，結果表明該方法的預測優化是可行和有效的。上述方法盡管都能較為準確的對未來時刻的行為作出預測，但無法克服數據波動對預測效果帶來的負面影響。本文提出了一種K-均值聚類與GRU神經網絡相結合的模型——K-GRU模型，通過K-均值聚類處理能夠降低據波動導致的時間序列內部差異，有利于GRU神經網絡更好地作出預測。

本文對不同分布下構造的時間序列進行了仿真實驗。通過不同場景中的仿真實驗得到預測誤差，再與多項式模型、傅里葉序列、LSTM模型和GRU模型進行比較，仿真結果表明本文所提的K-GRU混合模型具有較高的預測精度，最后將K-GRU混合模型應用于街邊停車位占用率預測。

1 K-GRU混合模型

本節介紹了K-GRU混合模型相關的理論知識，并給出了算法步驟。

1.1 GRU神經網絡

GRU是LSTM網絡的一種效果很好的變體。它和LSTM一樣具有門控循環單元，而GRU神經網絡僅需要兩個門控循環單元即可解決梯度消失和梯度爆炸的問題。因此，它比LSTM網絡的結構更加簡單，而且訓練速度也更快。具體結構如圖1所示。

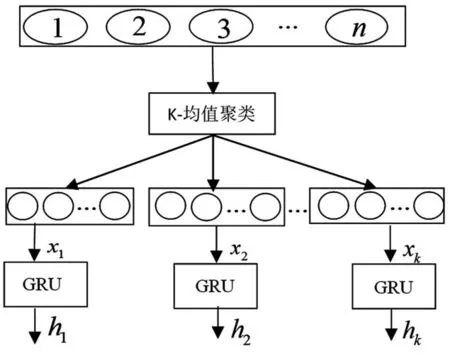
圖1 GRU模型結構圖

在GRU模型中只有兩個門，分別是重置門rt和更新門zt。重置門控制前一時刻狀態有多少信息被寫入到當前的候選集上，重置門越小，前一狀態的信息被寫入的越少。更新門由LSTM中的遺忘門和輸入門結合而成，更新門的作用是控制前一時刻的隱藏狀態信息被轉移到當前狀態中的程度，更新門的值越大說明前一時刻的狀態信息轉入越多，相反，更新門越小，前一狀態的信息被轉入得越少。

其中，w、u、wr、ur、wz、uz為神經網絡權值；t為時間步長；xt為輸入值；?t為輸出值；⊙為不同矩陣的Hadamard積；yt為當前時刻輸出值。

1.2 基于聚類的K-GRU混合模型

聚類是數據挖掘和分析的主要研究領域之一。常用的聚類方法有K-均值聚類［8-9］、層次聚類［10-11］、SOM 聚類［12-13］等。

K-均值聚類算法由于在處理大量數據方面的簡單性和速度而在以前的研究中被認為是一種廣泛使用的聚類算法［14］，因此本文采用K-均值對混合分布的時間序列數據進行聚類。通過K-均值聚類可以把較長的時間序列按K個初始聚類中心進行聚類，將原本單個的時間序列聚為K個序列，達到降低序列內部差異的效果。K-均值算法需要計算各個樣本點到中心點的距離，常用的距離為歐氏距離，計算公式如下：

基于聚類的GRU混合模型的結構圖，如圖2所示。

圖2 基于聚類的K-GRU混合模型

具體步驟如下：

（1）數據采集和數據預處理。可通過計算機語言生成模擬實驗數據或數據網站下載相關數據。然后進行數據清洗、刪除或補齊缺失值、歸一化等。

（2）K-均值聚類。使用K-均值對步驟（1）中得到的數據進行聚類。

（3）劃分樣本。對每個類都進行訓練集與測試集的劃分，劃分比例為8∶2。

（4）GRU神經網絡訓練。使用劃分好的訓練集進行神經網絡的訓練。

①第一層為GRU層，設置輸入維度、輸出維度和 return_sequences、return_sequences為 False，返回單個時間步長的隱藏狀態的值，若為True，則返回全部的隱藏狀態值。

②設置Dropout即隨機失活率，Dropout是在訓練過程中隨機地忽略一些神經元，它會刪除一些節點，以及網絡與被刪除節點之間的連接。

③第二層為GRU層，輸入維度即為上一層的輸出維度，設置return_sequences以及Dropout的取值。

④第三層是全連接層Dense層，網絡訓練的損失函數選擇均方誤差，選擇優化器rmsprop。

（5）輸入測試樣本進行測試。

（6）計算并輸出預測誤差。通過對神經網絡參數的調整，以達到誤差最小。

本文的算法流程如圖3所示。

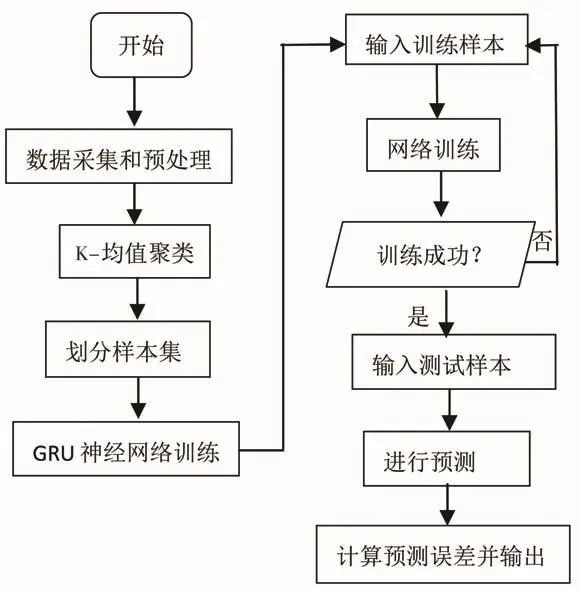
圖3 算法流程圖

2 仿真實驗

為評價模型的性能，利用隨機生成的數據進行了一系列的模擬實驗。在python3.7環境下使用tensorflow2.0訓練預測模型，實驗計算機的物理核心為8核，邏輯核心為4核，顯存大小為2 G，內存為32 G，儲存空間為1 T。

2.1 評價標準

為了便于比較不同方法在占用率預測實驗中的表現，使用平均絕對誤差（Mean absolute error，MAE）和均方誤差（Mean squared error，MSE）來描述實驗誤差。

平均絕對誤差（Mean absolute error，MAE）：

均方誤差（Mean squared error，MSE）：

2.2 仿真實驗及分析

本節分別在三個場景中比較了多項式模型、傅里葉變換、LSTM模型、GRU模型與GRU混合模型的預測效果。設置樣本量為n=5 369，其中場景A表示由數據量為5∶2的兩個時間序列數據構成，分布分別為N～（0.3，0.1）和N～（0.2，0.09）；場景B表示由數據量為5∶2的兩個時間序列數據構成，分布分別為 N～（0.3，0.1）和 Be～（0.19，0.66）；場景C表示生成均值為0.25，標準差分別為0.1～0.5的正態分布。模擬實驗數據均使用R語言生成。

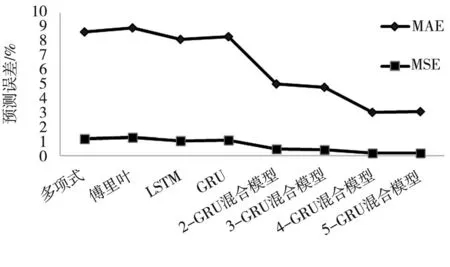
圖4 場景A各方法預測誤差比較

表1為場景A中各方法預測誤差的具體數值，可以看出多項式模型、傅里葉序列、LSTM模型和GRU模型的預測效果幾乎一致，K-GRU混合模型預測效果明顯優于前面四種方法。KGRU混合模型在聚類數為4時，MAE和MSE都降到最低，分別為3.008%和0.170%，而當聚類數為5時，MAE和MSE都比聚類數為4時的MAE和MSE稍大。通過圖6也可以看出，K-GRU混合模型的預測效果顯著優于前面四種方法（標注*的數字為最佳預測結果）。

表1 場景A各方法預測誤差

表2為場景B中各方法預測誤差的具體數值，可以看出多項式模型、傅里葉序列、LSTM模型和GRU模型的預測效果幾乎一致，K-GRU混合模型預測效果明顯優于前面四種方法。K-GRU混合模型隨著聚類數增加，MAE和MSE都在下降，但聚類數為5時，MAE和MSE的下降幅度明顯變小。通過圖5也可以看出，K-GRU混合模型的預測效果顯著優于前面四種方法，且聚類數為5時，誤差下降幅度明顯減緩（標注*的數字為最佳預測結果）。

表2 場景B各方法預測誤差

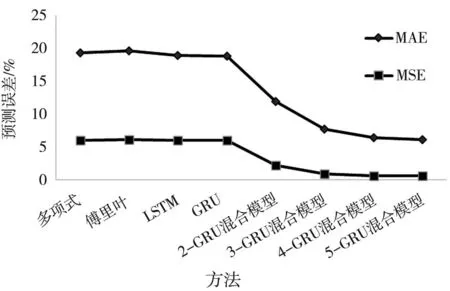
圖5 場景B各方法預測誤差比較

圖 6（a）和圖 6（b）分別為場景C中各方法預測的MAE和MSE，可以看出在樣本量固定的情況下，隨著標準差的增加，并未對預測結果的MAE和MSE造成較大的波動，說明預測模型具有魯棒性。K-GRU混合模型在聚為2類、3類、4類和5類的情況下都比多項式模型、傅里葉序列、LSTM模型和GRU模型的預測效果更好，隨著聚類數的增加，K-GRU混合模型的MAE和MSE的下降幅度變緩。

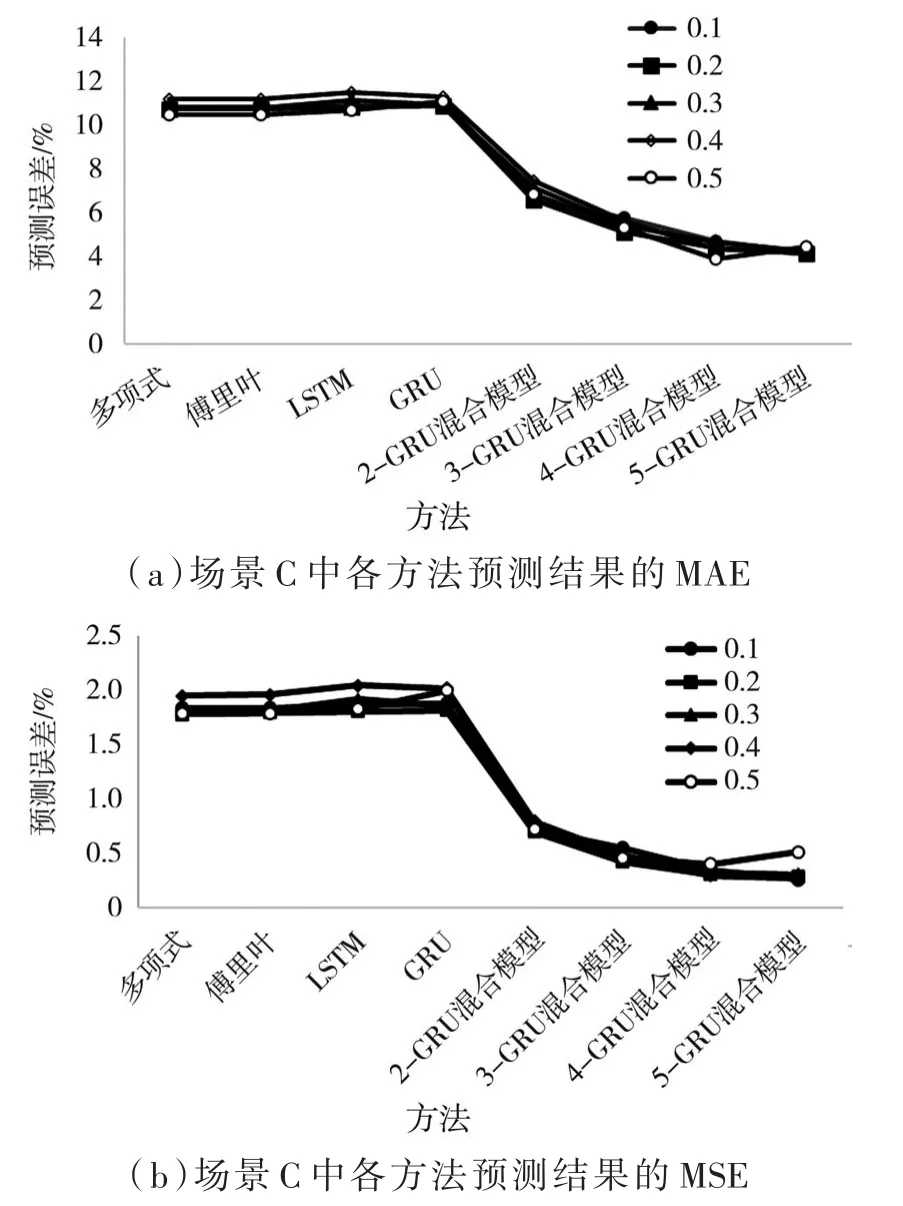
圖6 場景C中各方法預測的MAE及MSE

3 實證分析

本文使用的數據是2018年12月1日到2019年2月28日深圳市南山區招商路90天的歷史街邊停車數據。在該數據集中，記錄到招商路總共59個有效停車位，共計18 899條停車記錄。圖7是招商路的地理位置及街邊實景圖。

圖7 招商路百度地圖及街邊實景圖，有效停車位共59個

在數據預處理過程中，數據按10 min的時間間隔統計停車位的占用數量，并根據總的有效停車位數量計算街邊停車位的占用率。經過數據預處理后，可以得到時間從10：10分到19：50分，共計5 310條時間間隔為10 min的街邊停車位占用率數據。招商路三個月的停車位占用率變化趨勢如圖8所示。

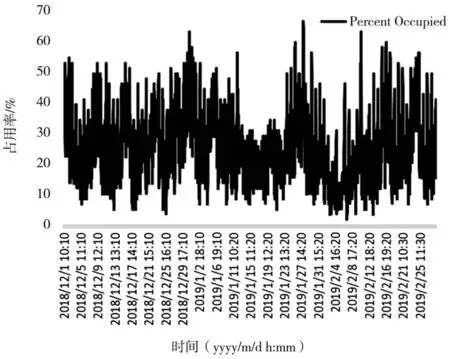
圖8 招商路的停車位占用率

通過圖8可以看出，招商路的街邊停車占用率符合一般的停車規律，即周末占用率普遍偏高，工作日的占用率普遍偏低，可看作是以一個星期為周期的時間序列。

根據圖8，對招商路的周末和工作日占用率數據進行描述統計，分別得到兩個Q-Q圖，如圖9和圖10，可以看出周末的占用率服從正態分布，工作日的占用率服從beta分布。

圖9 招商路周末的街邊占用率正態Q-Q圖

圖10 招商路工作日的街邊占用率beta Q-Q圖

將K-GRU混合模型應用于招商路的實際占用率數據，并與多項式擬合、傅里葉級數、LSTM、GRU四個方法進行了比較。其中多項式和傅里葉級數的階數分別取8和12，LSTM和GRU的激活函數為 linear，epochs為 30，bitch_size為 500，訓練集與測試集的比例均為8∶2。實驗結果如表3所示。

表3 招商路各方法預測結果

由表3可以看出，K-GRU混合模型的實驗誤差比多項式模型、傅里葉序列、LSTM和GRU都小。隨著聚類數的增加，MAE和MSE都在下降，但聚類數為5時，混合模型的預測誤差開始上升。聚為4類時，K-GRU混合模型的表現最好，MAE為3.315%，MSE為0.173%。

圖 11（a）和圖 11（b）分別為招商路各方法占用率預測的MAE和MSE值的條形圖，可以看出使用多項式模型和傅里葉序列進行預測的實驗誤差很高，LSTM、GRU和GRU混合模型的實驗誤差都明顯低于前兩種方法。在混合模型中，實驗誤差隨著聚類數增加而降低，聚類數為4時，MAE和MSE都達到了最低，分別為3.315%和0.173%，但聚類數達到5時，MAE和MSE略微上升。

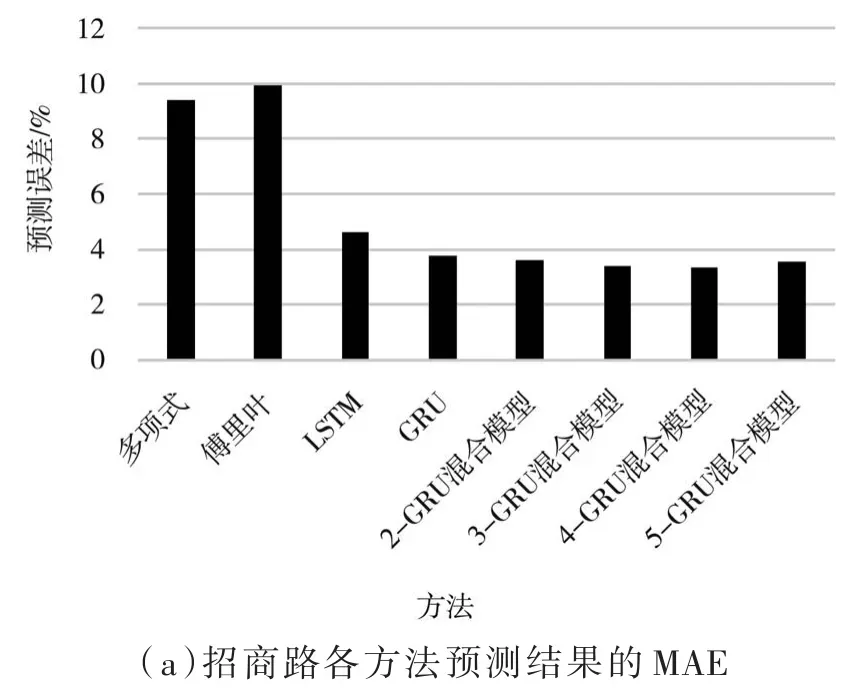
圖11 招商路各方法預測結果的MAE及MSE

從圖 12（a）和圖 12（b）可以看出，K-GRU 混合模型在分別聚為2類、3類、4類和5類時預測的MAE比多項式模型和傅里葉序列預測的MAE下降比例超過了60%，MSE比多項式模型、傅里葉序列的MSE下降比例超過了80%。K-GRU混合模型在聚類處理后MSE比LSTM的MSE下降超過40%。K-GRU混合模型的MSE比GRU的MSE下降超過20%。聚類數達到4的時候，MAE及MSE下降百分比達到最高。

圖12 K-GRU混合模型預測的MAE及MSE下降的百分比的條形圖

4 結論

本文提出了K-GRU神經網絡混合模型，使用K-GRU混合模型對混合分布下的時間序列數據進行預測。利用R語言隨機生成的數據進行了仿真實驗，并且將混合模型應用于實際的街邊停車位占用率預測中。與多項式回歸模型、傅里葉級數、LSTM神經網絡、GRU神經網絡相比，本文所提的方法具有較低的預測誤差。通過仿真實驗結果，K-GRU混合模型在聚類數為4時，通常能得到最佳預測效果。而聚為5類時，預測誤差下降幅度變緩甚至會略微上升。其原因是固定樣本量的條件下，隨著聚類數增加，每個類的樣本量變小，神經網絡從單個類中無法學習到完整的信息。