光纖光柵傳感器振動與溫度信號解耦

李 晗， 張波濤， 王俊杰， 孫運達， 龔圣捷

(上海交通大學 核科學與工程學院，上海 200240)

隨著核電技術的進步與發展，安全問題已經成為核電發展的主要挑戰.為保障核電站安全運行，需要對核電站運行中的各種信號進行實時監測，主要涉及核電站中設備以及部件、管道的振動與溫度監測，混凝土結構的應變以及堆內溫度監測等[1].傳統的電學傳感器在核電站安全監測領域已經廣泛應用，但其存在零點漂移、惡劣環境下壽命短、可靠性低、無法實時監測以及測量信號單一等問題，尤其是在需要對溫度與振動信號同時監測的場景，一方面是對核電廠主蒸汽管道、核電廠輸油管道泄漏的實時監測，另一方面是對核廢料堆內以及核電廠運行燃料組件內信號的實時監測，目前對振動、溫度等重要參數的同步實時測量技術仍需改進.光纖光柵傳感器尺寸小，可實現分布式多點測量，并且具有抗電磁干擾、耐高溫、耐輻射、易于實現遠程實時測量以及多信號測量等優點，可以實現對現行核電站運行關鍵參數的實時監測.日本核能研究院研究了輻射環境下光纖光柵(FBG)的可靠性，得出其在整個反應堆壽命期間能承受核輻射考驗的結論[2].

利用FBG傳感器同時測量獲得振動與溫度信號，必須要解決兩者交叉敏感的問題，目前研究中解決交叉敏感問題的主要方法有：雙波長矩陣法、雙參量矩陣算法、溫度參考光柵法以及溫度補償封裝法等，而這些方法的原理均基于雙波長矩陣法[3].這種方法的基本思想是建立一個關于溫度和應變的線性方程組[4]，然后對線性方程組進行求解，最終獲得溫度值與應變值.文獻[5]以兩個FBG和一個長周期光纖光柵為傳感單元，對應變和溫度進行測量.文獻[6]也以雙參量測量為基本思想，采用一種超結構FBG作為傳感器，測量其透射譜，讀取光強和Bragg波長的變化量，從而實現對應變和溫度的同時測量.文獻[7]針對室溫化學固化型義齒基托樹脂在凝固過程中同時產生收縮應變和放熱現象，將化學鍍鎳FBG 與裸 FBG 相結合，設計出一種新的測量結構，實現了溫度和應變雙信號的同時測量.文獻[8]將兩個中心波長不同的FBG重疊寫入光纖同一位置，同時測量溫度與應變，通過測量兩個FBG的波長漂移求解矩陣，從而實現同時測量.文獻[9]為解決FBG傳感器溫度和應力交叉敏感的問題，研究了一種FBG雙信號傳感器，不僅能夠有效地去除溫度交叉敏感問題，同時還可以實現溫度和應力兩種信號的準確測量.上述雙波長矩陣法要求傳感器中FBG的個數至少為兩個，且兩者中心波長有明顯差異，使傳感器的結構復雜且尺寸較大，難以滿足核電站關鍵參數的實時監測需求.

針對現有的核電站運行信號監測需求，基于FBG傳感器對振動信號與溫度信號的響應特性差異，本文提出采用單個FBG傳感器測量振動與溫度復合信號的信號解耦方法，并通過實驗進行驗證，本文的研究成果可為簡化核電站運行監測系統以及提升監測精度提供實驗基礎.

1 原理

1.1 FBG傳感原理

布拉格FBG是利用光纖材料的光敏性在纖芯內形成折射率周期分布的空間相位光柵, 其實質是一窄帶濾波器或反射鏡.結構示意圖如圖1(a) 所示，主要包括外部光纖、內部纖芯以及全息寫入光柵.FBG的反射透射特性如圖1(b)所示.其中：I為光強；λ為光波長；λb為反射光中心波長.通入寬帶光的入射光譜，經過FBG后一部分會透過FBG成為透射光譜，還有一部分具有特定波長的光被反射回來成為反射光譜，反射光譜的波長稱為FBG的中心波長，是由實驗直接測量獲得的物理量.

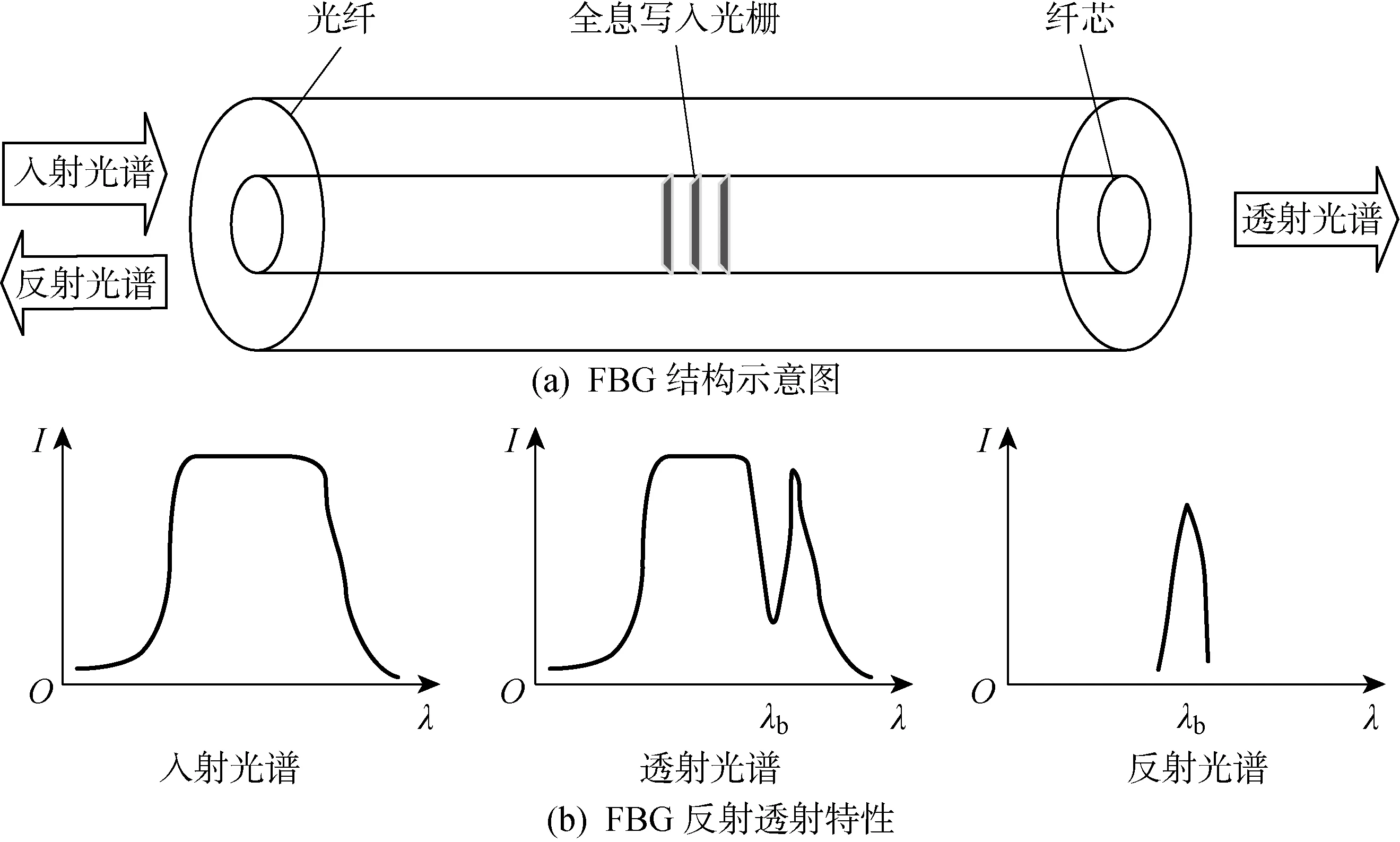
圖1 FBG結構與傳感原理示意圖Fig.1 Schematic diagram of FBG structure and sensing principle

由耦合模理論[10]，一個均質的FBG光譜響應是一個波峰中心位于λb的單峰.布拉格條件將中心波長λb表示為

λb=2neffT

(1)

式中：neff為FBG的有效折射率；T為FBG的周期.

外界的應變或者溫度變化都會造成FBG參數

的變化，如有效折射率或者周期的變化，二者都可以使反射回來的中心波長發生變化，通過追蹤中心波長的變化便可以獲得應變或者溫度的變化[9].由應變導致的FBG中心波長變化率可以表示為

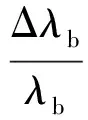
(2)

由溫度變化導致的FBG中心波長變化率可以表示為

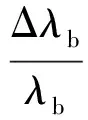
(3)

當光纖光柵同時受應變以及溫度變化作用時，FBG中心波長變化率可以表示為

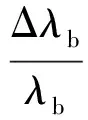
(4)

式中：Δλb為FBG中心波長的漂移量；ε1為由載荷導致的FBG應變值；ΔQ為溫度變化；Pe為FBG的光彈系數；αf為結構的熱膨脹系數；ξ為FBG的熱光系數.

1.2 算法原理

在振動測量實驗中得到的信號，往往會由于傳感器頻率范圍不穩定或者外界環境干擾等因素，產生偏離基線的情況，這種偏離基線隨時間變化的過程叫做信號的趨勢項.在一般工況下，溫度信號周期性不明顯，而振動信號具有明顯的周期性.因此，可將溫度信號視作多項式趨勢項并從復合信號中分離，以達到溫度信號和振動信號解耦的目的.常用的消除趨勢方法主要有小波法與最小二乘法，有研究發現，對于確定性信號最小二乘法在其線性和多項式趨勢項的提取上均比小波法的效果好，與原始信號更為接近[11].由于本文振動響應曲線為使用激振器輸入的確定性信號，所以采用最小二乘法進行信號解耦.

最小二乘法[12]既可以消除呈線性狀態的基線偏移，又可以消除具有高階多項式的趨勢項.其主要計算步驟為：① 假設趨勢項為某一種模式，采用最小二乘法原理列出求解的方程；② 使用矩陣法求出趨勢項系數矩陣，并得出趨勢項的擬合曲線；③ 將趨勢項與原始信號分離實現兩種信號的解耦.

(5)

式中：bj為第j項多項式系數.

sn點的集合是sn中多項式各組成部分的估計值，根據最小二乘法的原理，假設函數E(Δt)為實際值與估計值之間的誤差平方和，可以得到：

(6)

將E(Δt)對bj取偏導數，令其值為0，整理可以得到k+1個方程為

(7)

當k=1時，得到趨勢項系數矩陣為

(8)

當k=2時，得到趨勢項系數矩陣為

(9)

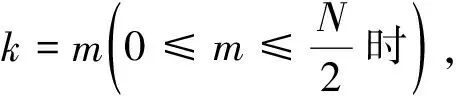
(10)

當k≥2時，上述矩陣為曲線趨勢項.為盡可能與實際情概況相近，將原始信號劃分為多段，在每一段上采用不同的k值進行信號解耦，最終將解耦得到的信號進行整合.

1.3 程序實現

基于MATLAB 2019軟件平臺，通過編程對上述算法進行實現.為驗證上述算法的可行性，進行了仿真實驗，仿真輸入信號y為

(11)

該仿真輸入信號由一個正弦振動信號和一個三次多項式趨勢項組成，其波形圖如圖2(a)所示；使用上述算法解耦得到的信號如圖2(b) 和2(c)所示，分別為正弦振動信號與趨勢項；將解耦信號與輸入信號進行對比，如圖2(d)和2(e)所示.其中：yp-ad為解耦后的多項式趨勢項；ys-ad為解耦后的正弦項；ys為正弦項；yp為多項式趨勢項.由圖2(d)和2(e)可知，解耦信號與原始信號重合度高，說明該算法的程序可靠性好，可以用于后續實驗驗證與評價.

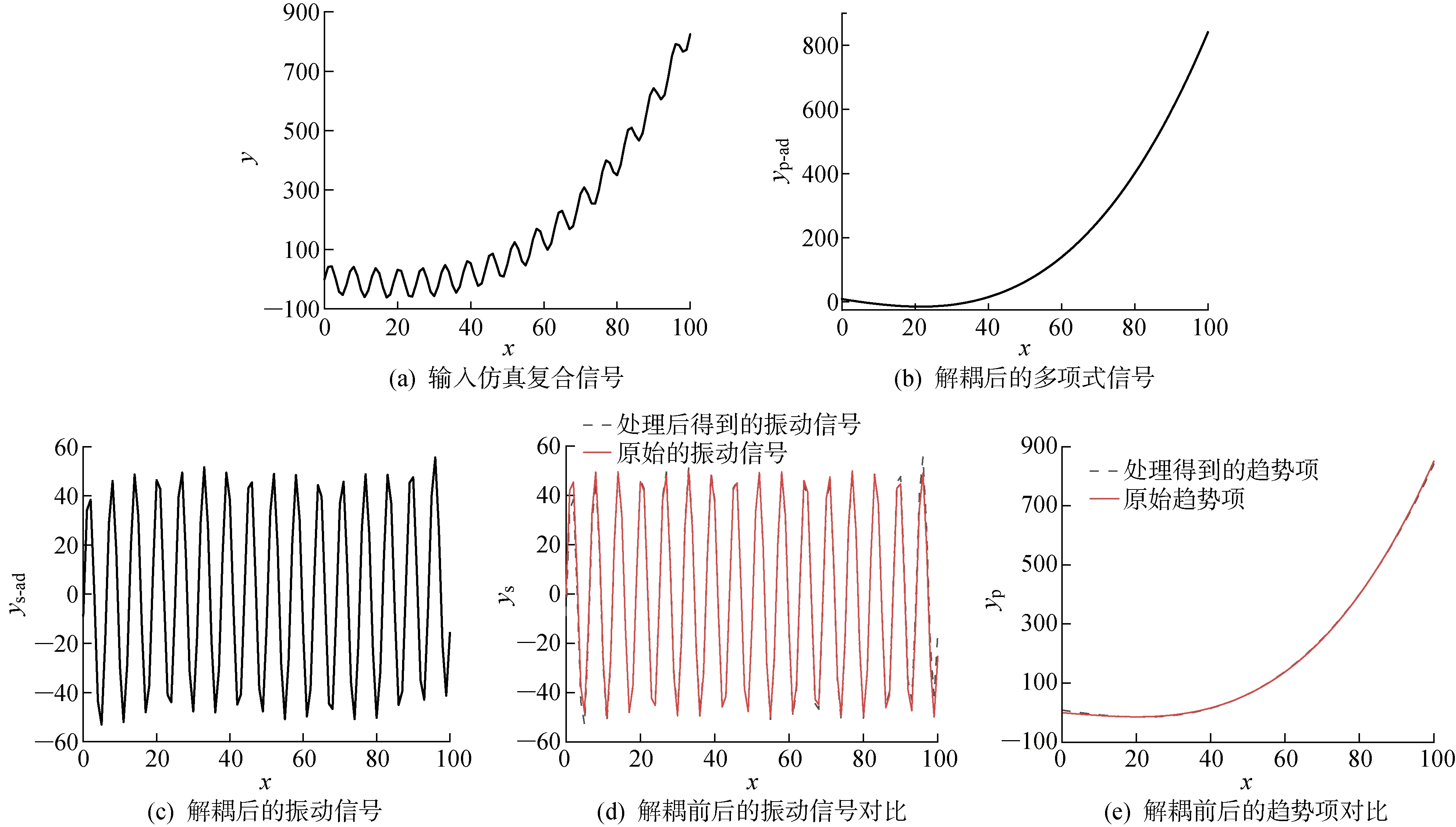
圖2 程序處理前后的信號波形圖Fig.2 Signal waveforms before and after program processing

2 實驗驗證

2.1 實驗裝置與內容

實驗系統由五部分組成，如圖3所示.其中：NI為熱電偶溫度測量系統; LDV為激光多普勒測振儀.激振系統由函數發生器、信號放大器以及激振器組成，可以產生特定頻率、振幅的振動信號；加熱系統通過電加熱器對實驗段的介質進行加熱、控溫，并產生溫度信號；FBG傳感器測量系統，通過FBG傳感器對測點位置的振動與溫度信號進行同步測量，經FBG解調儀將復合信號傳輸給計算機；振動信號測量系統使用激光多普勒測振儀對測點位置的振動信號進行測量；溫度信號測量系統使用標準K型熱電偶對測點位置的溫度信號進行測量.實驗件為直徑為9.5 mm、長度為520 mm的圓柱棒，置于內徑為80 mm、長度為500 mm的亞克力管道內，實驗頻率為20 Hz，溫度變化范圍為26～80 ℃.

圖3 實驗系統示意圖Fig.3 Schematic diagram of experimental system

實驗段示意圖如圖4所示.實驗件通過螺紋孔固定在法蘭盤上，可視化亞克力管道內以去離子水為介質.實驗分別在3種工況下開展：① 開啟加熱系統，獲得輸入信號為單一溫度信號時，FBG傳感器測量系統的響應，研究FBG傳感器的溫度測量；② 開啟激振系統，獲得輸入信號為單一振動信號時，FBG傳感器測量系統的響應，研究FBG傳感器的振動測量；③ 同時開啟加熱和振動系統，獲得輸入信號為振動-溫度復合信號時，FBG傳感器測量系統的響應，研究FBG傳感器溫度-振動信號的解耦行.

圖4 實驗段示意圖Fig.4 Schematic diagram of experimental section

2.2 溫度信號靜態測量實驗

為驗證信號解耦方法的準確性，控制實驗系統使輸入為單一溫度信號，采用FBG傳感器測量系統與溫度測量系統對FBG傳感器溫度測量特性進行分析與評價.將實驗系統在無振動信號干擾的情況下運行，通過電加熱器加熱流道內去離子水，控制溫度變化范圍為26～80 ℃.為保證測量結果的準確性進行了重復性實驗，最終得到FBG傳感器的溫度響應曲線以及誤差值分布如圖5所示.其中：Qth為熱電偶溫度；ΔQFBG為FBG溫度差值.所得到的溫度Q的擬合方程為

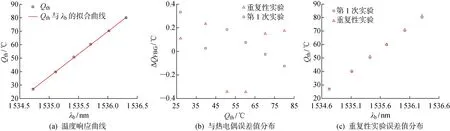
圖5 溫度靜態測量實驗結果Fig.5 Experiment results of temperature static measurements

Q=33.557 59λb-51 474.651 5

(12)

其線性擬合度R2=0.999 7.

由圖5(a)可知，FBG傳感器在對溫度進行測量時具有很好的線性響應靈敏度，使用直線擬合法得到其溫度靈敏系數為 0.029 79 nm/℃.由圖5(b)和5(c)可知，在實驗溫度變化范圍內，兩次實驗FBG傳感器溫度測量值與標準熱電偶的誤差值均在 ±0.4 ℃以內，重復性實驗誤差值在 ±0.7 ℃以內，可以滿足工程中應用的要求，且FBG傳感器的信號采集頻率遠高于熱電偶，在實際測量中可對溫度進行實時監測，具有較好的測量精度與較大的測量范圍.

2.3 振動信號動態測量實驗

控制實驗系統使輸入為單一振動信號，啟用FBG傳感器測量系統與LDV振動測量系統對FBG傳感器振動測量特性進行分析與評價，其中振動信號的數據采集頻率為 8 192 Hz.將實驗系統置于恒定溫度條件下，分析FBG傳感器對輸入振動信號的響應，獲得其動態響應，并將FBG與LDV的測量結果作對比分析.

通過信號發生器產生白噪聲信號驅動激振器對實驗件進行激勵，由FBG傳感器獲得的時域動態響應特性與頻域動態響應特性分別如圖6(a)和6(b)所示.其中：AFBG為FBG振動幅值；f為頻率.從實驗件的頻域動態響應特性可以得到其固有頻率，在實驗過程中采用頻率遠離試驗件固有頻率的正弦信號，以防止共振對實驗系統產生危害.

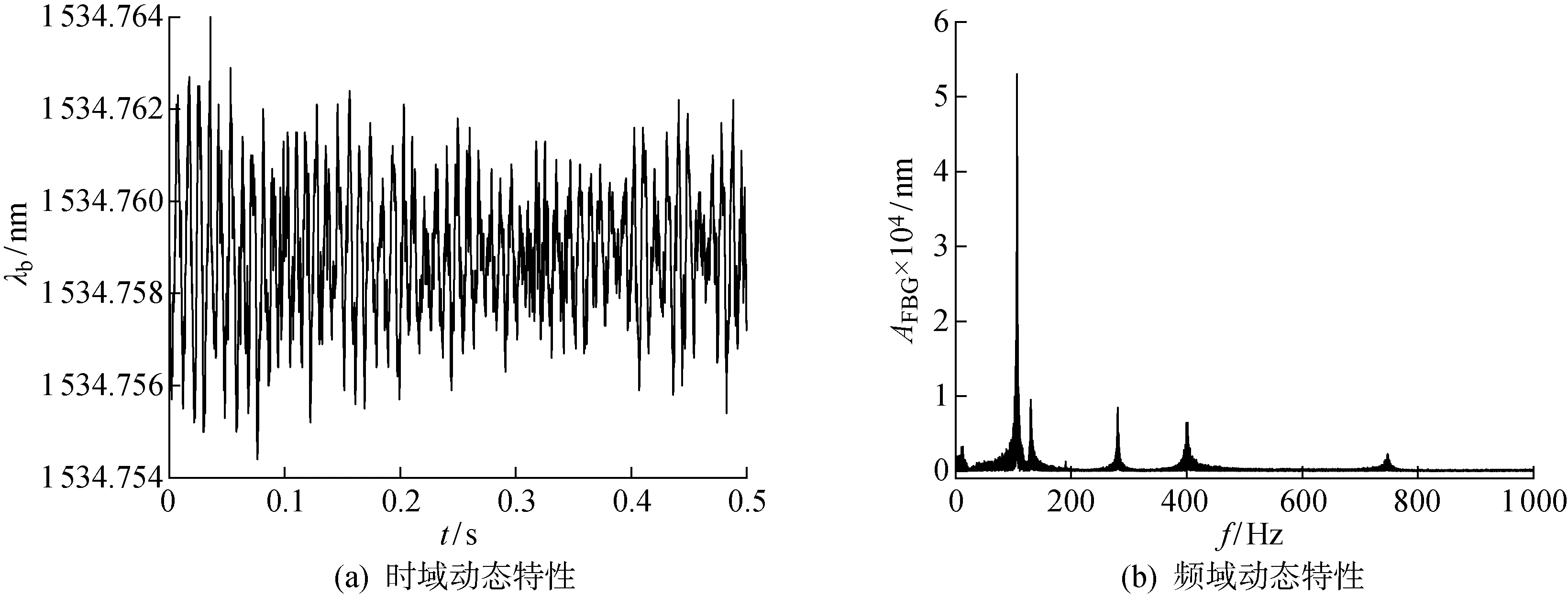
圖6 白噪聲FBG振動測量實驗結果Fig.6 Experiment results of FBG vibration measurements

采用20 Hz的正弦信號對實驗件進行激勵，獲得的時域動態響應特性與頻域動態響應特性如圖7所示. 其中： Δλbo為FBG原始中心波長漂移；sLDV為LDV位移；ALDV為LDV振動幅值.由圖7(c)可知，FBG傳感器測得的主頻為19.90 Hz，幅值為0.001 4 nm；由LDV測得的主頻為20.00 Hz，其主頻相對誤差為0.50%，表明FBG傳感器能準確測量振動信號的頻率.

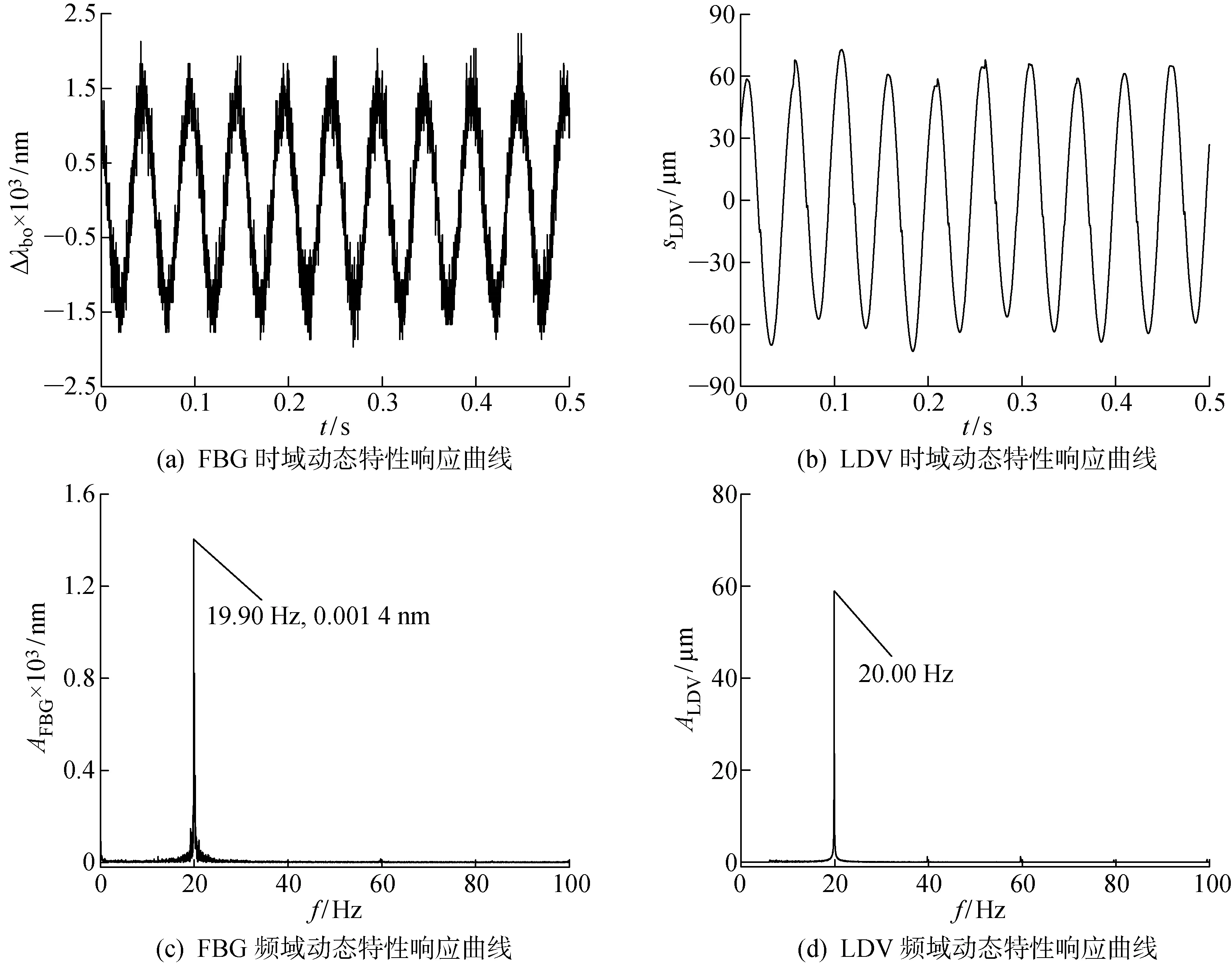
圖7 振動動態測量實驗結果Fig.7 Experiment results of vibration dynamic measurements

2.4 復合信號測量實驗

為研究信號解耦方法的有效性和準確性，控制激振器和加熱器輸入振動-溫度復合信號，使用FBG傳感器對復合信號進行測量.將FBG傳感器得到的復合信號使用上述方法解耦得到振動信號與溫度信號，并對其進行誤差分析，綜合評價信號解耦方法的可行性.

通過激振系統產生與單一振動信號動態測量實驗相同的振動信號，同時通過電加熱器控制溫度變化，FBG傳感器測得的復合信號如圖8所示，其中：λb-bd為解耦前的FBG中心波長.熱電偶測得的溫度信號如圖9所示.

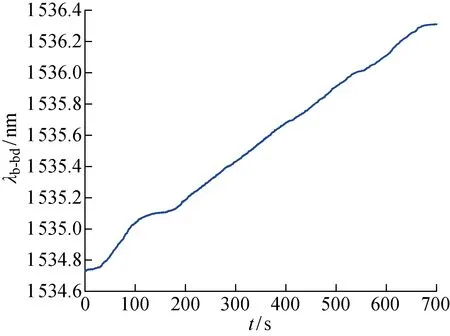
圖8 FBG復合信號響應曲線Fig.8 Response curve of FBG composite signal

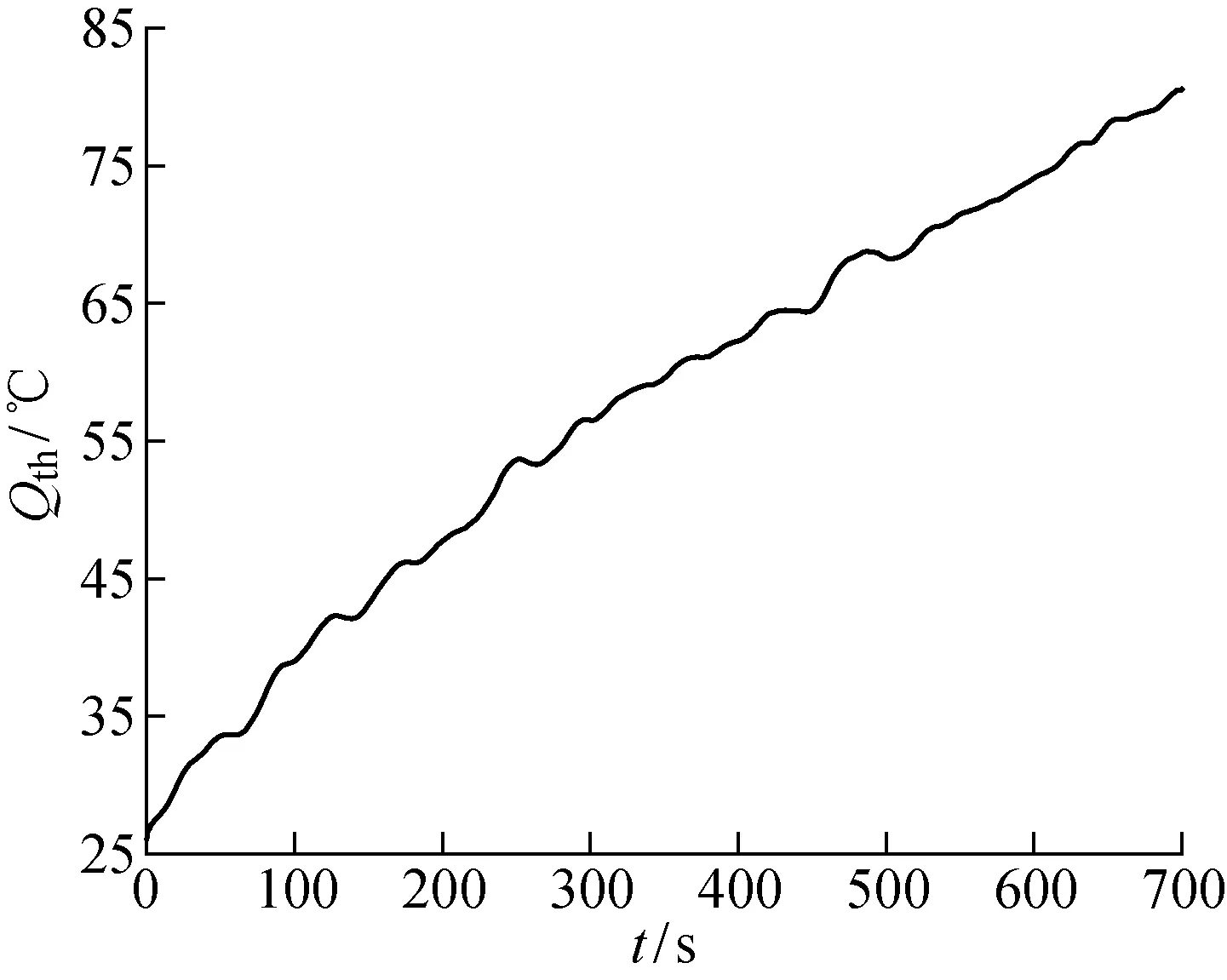
圖9 熱電偶溫度信號響應曲線Fig.9 Response curve of thermocouple temperature signal

3 實驗結果分析

3.1 誤差分析

根據上述實驗方法，利用信號解耦程序將FBG傳感器得到的復合信號進行處理，得到解耦后的FBG溫度QFBG-ad、解耦后的FBG振動幅值AFBG-ad以及解耦后的FBG主頻fFBG-ad；由溫度測量系統與振動測量系統分別測得輸入信號，得到熱電偶溫度Qth、FBG原始振動幅值AFBG-o以及FBG原始主頻fFBG-o.為驗證信號解耦方法的準確性，本文對由FBG測量結果解耦得到的信號值與輸入信號值進行對比分析.以主頻相對誤差為例，相對誤差η計算方法[14]如下：

(13)

Δf=fFBG-o-fFBG-ad

3.2 實驗結果

利用上述信號解耦程序對復合信號進行處理，為提高信號解耦的精確度，在實際處理過程中將復合信號分為多段區域進行信號解耦處理，再將得到的結果進行整合，與單一信號測量系統得到的結果進行比較.以其中的一段5 s時長的信號為例，信號解耦結果如圖10所示.其中：Δλb-ad為解耦后的FBG中心波長漂移.

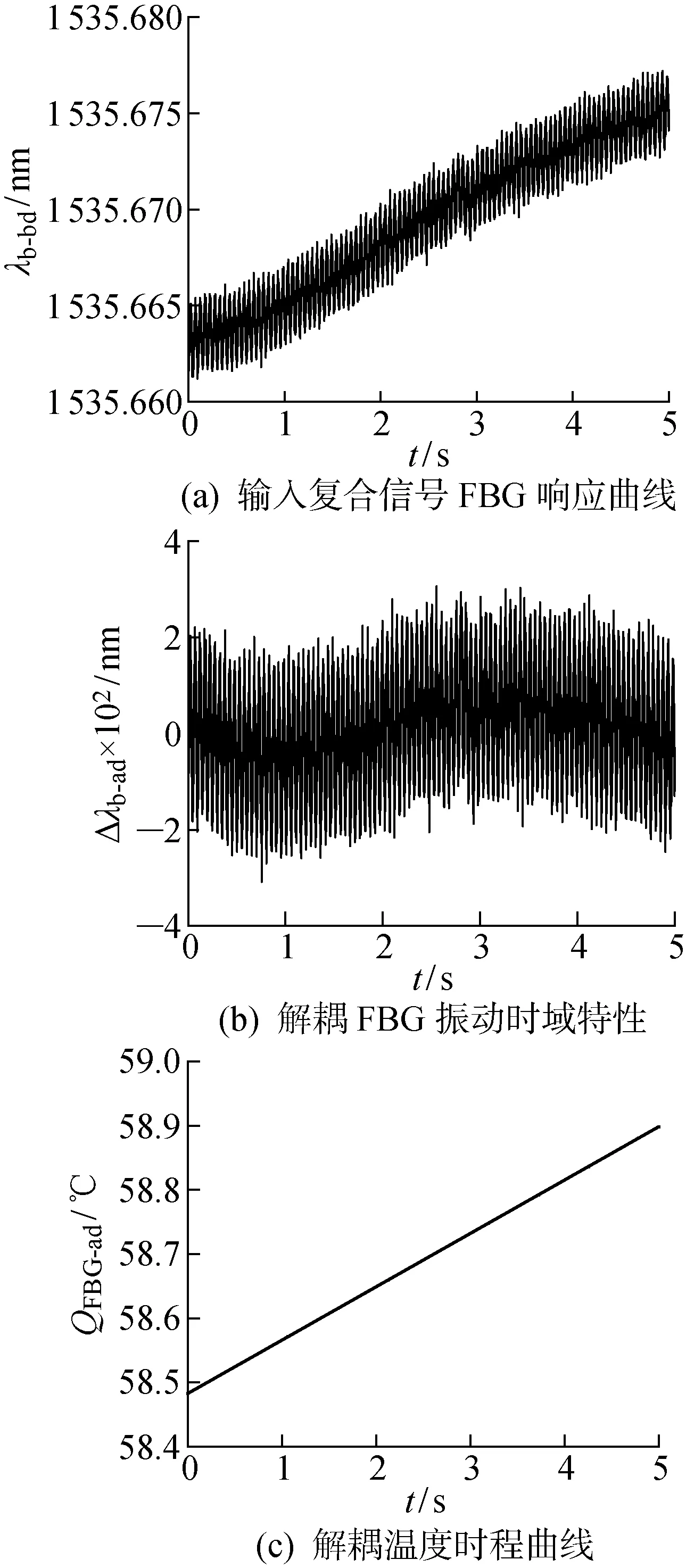
圖10 信號解耦效果示意圖Fig.10 Schematic diagram of signal decoupling effects

3.3 振動信號誤差分析

通過信號解耦方法得到的振動信號響應曲線如圖11所示.由圖可見，主頻為19.77 Hz，幅值為 0.001 3 nm.與圖7(c)的信號進行對比，主頻相對誤差0.65%，幅值相對誤差7.14%.說明由解耦方法得到的振動信號能正確反映輸入振動信號的頻域響應特性與時域響應特性，且相對誤差較小，在實際測量中能滿足精度要求，滿足可行性與準確性要求.

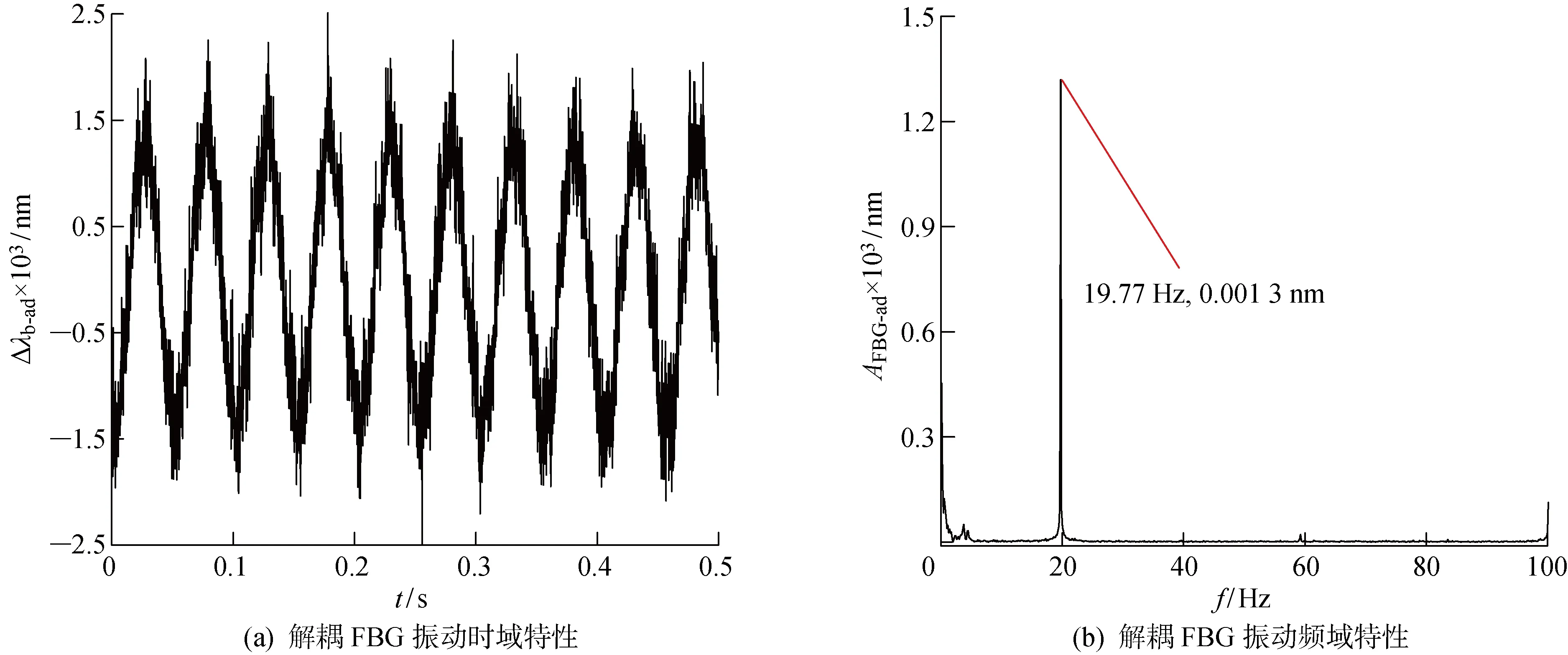
圖11 解耦FBG振動信號Fig.11 Vibration signals of decoupling FBG

3.4 溫度信號誤差分析

溫度信號在0～700 s時間內溫度由26 ℃逐漸變為80 ℃，解耦溫度信號與熱電偶信號對比如圖12所示.由圖12可知，溫度變化的整體趨勢具有一致性，可以正確反映溫度變化的趨勢.溫度誤差分析如圖13所示.由圖13可知，溫度誤差均在 ±3.3 ℃以內.說明由解耦方法得到的溫度信號可以正確反映輸入溫度信號的變化趨勢，且相對誤差較小，在較大的測量范圍內可以實現對溫度的實時監測.

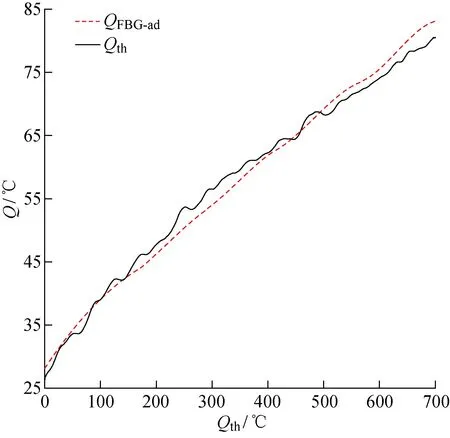
圖12 解耦溫度與熱電偶溫度對比Fig.12 Comparison of decoupling and thermocouple temperatures

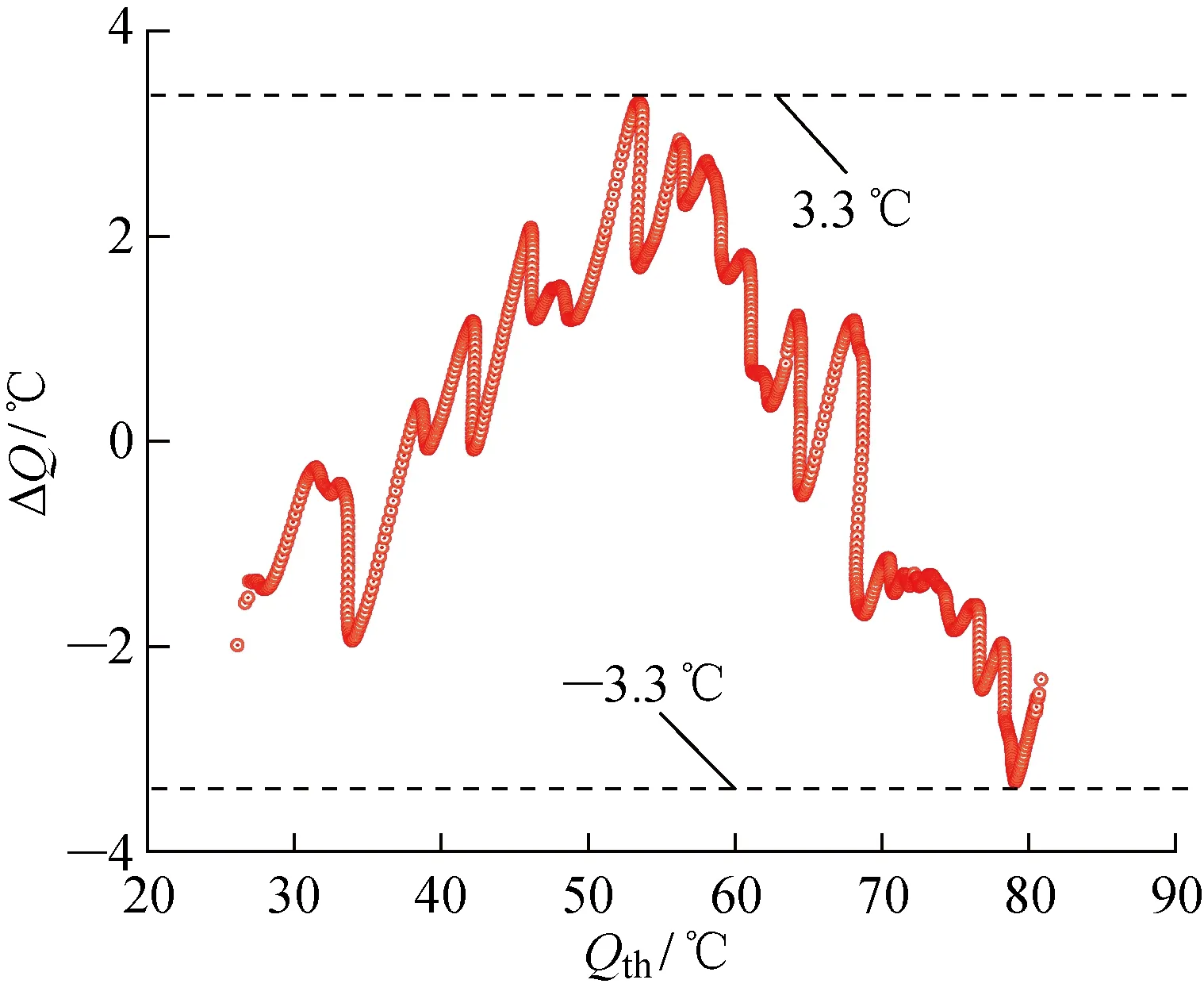
圖13 溫度誤差分析Fig.13 Analysis of temperature errors

4 結論

本文采用單個FBG傳感器測量振動-溫度復合信號，并通過最小二乘法進行解耦，分別獲得振動和溫度信號，該方法可用于對核電站關鍵部件和設備的振動、溫度信號進行實時監測，以確保核電站安全運行.通過實驗，在20 Hz振動頻率以及26～80 ℃溫度變化范圍內，對FBG傳感器的測量特性進行分析，并對所提出的最小二乘法信號解耦方法進行了驗證，主要結論如下.

(1) FBG傳感器對單一溫度信號的靜態測量具有很好的線性響應靈敏度，其溫度靈敏系數為 0.029 79 nm/℃，測量誤差值在 ±0.4 ℃以內，重復性良好.

(2) 采用LDV對FBG振動測量進行標定，振動主頻相對誤差為0.50%.

(3) 基于最小二乘法的信號解耦方法，對FBG測量的振動、溫度耦合信號進行分析，與熱電偶測量溫度值的誤差在 ±3.3 ℃以內；振動信號主頻為19.77 Hz，幅值為 0.001 3 nm，與輸入振動信號相比，主頻相對誤差為0.65%，幅值相對誤差為7.14%.