基于延誤成本的不正常航班調整策略研究
羅 軍,江林林
(中國民用航空飛行學院空中交通管理學院,廣漢 618307)
0 引言
在當代人的遠距離旅行中,航空出行扮演著舉足輕重的地位,日益增長的飛機數量造成航班正常率的不斷降低。天氣條件、機場保障等問題都是導致飛機延誤或取消的主要原因,給出行者造成了不便利的同時,航空公司和機場也承擔著經濟損失。但是由于航空的飛行安排已經非常嚴密,一旦某飛機受到影響,延誤會在航班串上產生多米諾效應,導致大量飛機晚點。及時合理地恢復延誤航班,確保恢復成本盡可能小,不能僅靠調度員,而采用最優化算法則可以迅速達到目標,在減少成本的同時還能將簽派員的工作效率提高,為后續飛機排班提供依據。
針對航班恢復問題,國內外已研究多年,也取得了相應的成果,賴俊曉[1]基于我國機隊規模小,將限制信息融入資源指派模型,構建了最小成本的航班恢復模型。為了提高航空公司效益,創造性地將改進的貪婪隨機自適應搜索算法運用于航班恢復模型中。戴福青等[2]將機會成本應用于航班恢復中,通過動態規劃算法將延誤航班損失降為原來的44%,證明了動態規劃算法在解決航班恢復問題時的可行性。李琳丹等[3]在非正常航班成本分析與優化方面,使用了三天內可用及新開航班結合的方法實施延誤航班恢復,利用LINGO 對延誤信息計算來減少恢復時間。姚韻[4]提出基于機號路徑置換算法,且用匈牙利法進行邊界約束求解。白鳳等[5]在航線不足和空港封閉而導致客機非正常飛行的情形下,通過列生成算法來求解構建的多商品網絡流模型。田倩南等[6]基于占優準則減少被恢復航線組合量,利用CPLEX 實現減小成本,提出了改進的時空網絡法。Teodorovi?等[7]結合機組及飛機路線恢復,使用字典序優化技術及分層優化技術,對新的機組進行排班重算。Vos 等[8]提出了一種新的動態建模框架,該框架可以針對飛機短缺問題解決已中斷的飛機時間表。Sinclair 等[9]在2016 年整合了航班和乘客恢復問題,通過混合規劃整數模型,并運用列生成算法來求解該模型。Petersen 等[10]將飛行計劃和線路、旅客等因素同時考慮,運用列生成法與Benders 分解來求模型,最后得出航班調整的具體計劃。
1 不正常航班問題描述
當航空公司原因或機場因為某些突發情況封閉,飛機原計劃飛行不能實施,這時要盡快調整航空公司飛行計劃,安排新飛行計劃。在航班計劃調整方面有三種調整策略,即飛機置換、航班延誤、取消航班[11]。由此可知,可以同時存在飛機的延誤成本和置換成本。
飛機置換是取消原執行該航班的飛機,將原不正常航班安排給其他飛機去執行,如圖1所示。
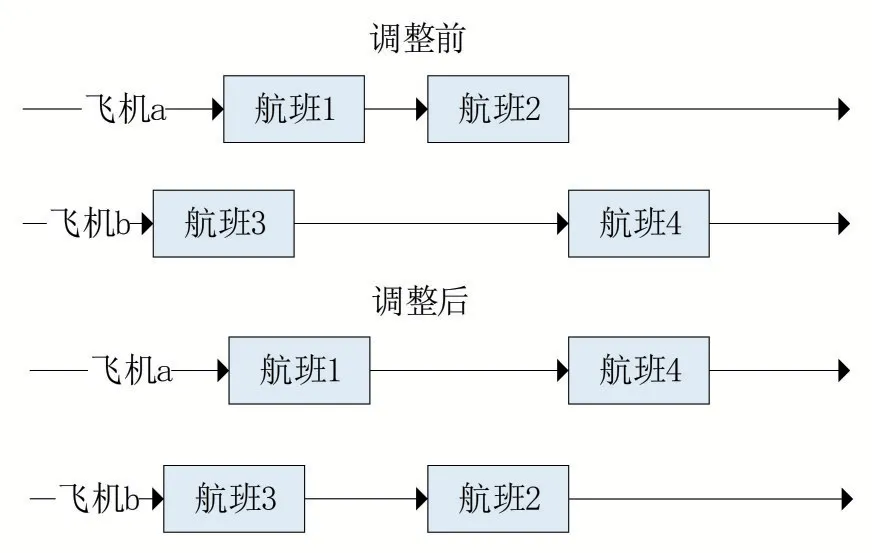
圖1 飛機置換圖
2 模型的建立
2.1 指派模型
航班恢復問題是在短時間內調整航班計劃而使延誤的成本最小化。所以,這類問題可看作指派問題。指派問題概念如下:
指派問題的簡單定義是:有n個人做n件事,如果已知第i個人做第j件事的總成本為cij(i,j=1,2,…,n),需要指定人和事之間一一對應的指派方案,使做這n件事的總成本最小。
設有n2個0-1變量,
數學模型為
2.2 航班恢復最小延誤成本模型
將不正常航班損失分為三種:航班取消成本、航班延誤成本、飛機置換成本。其中成本指標包括:
(1)飛機折舊費:飛機起飛前在地面等待時存在折舊費用,即ai。ai為一小時飛機的折舊費;為當飛機i執行航班f時停場時間。
(2)飛機停場費用:根據民航局規定,飛機停場2 h 以內免收停場費用;超過2 h,每停場24 h 按照起降費的15%計收。不足24 h 按24 h計收。當0≤≤2 時,bi=0。當>2 時,bi=[/24]×pi× 15%,bi為飛機停場費用,pi為起降費用,如表1 所示,Gi為飛機i的最大起飛重量。

表1 起降費用
(3)旅客賠償
民航局規定:延誤時間4~8 h,賠償標準不低于200元;延誤時間大于8 h,賠償不低400元。
(4)航班取消成本
航班取消成本按照該航班延誤大于8 h 計算。
基于指派模型,又建立了航班恢復目標函數如下:
約束條件如下:
注釋:飛機i執行航班f時,令=1,否則為0。飛機i執行航班f需置換時,令=1,否則為0。航班f需要取消時,令zf=1,否則為0。代表飛機i執行航班f時的旅客賠償費。pf為航班取消成本。pf1和pf2分別表示航班f上的經濟艙和商務艙旅客訂座數。qf1和qf2分別表示航班f上經濟艙和商務艙的機票價格。vi,wi表示飛機i上經濟艙和商務艙座位數。表示飛機i執行的前序航班的到達機場;表示飛機i執行的后序航班的出發機場。
2.3 改進的匈牙利算法
(1)確定飛機的到達和起飛機場,篩選出從該機場起飛的航班與飛機進行匹配,判斷是否滿足模型約束,直至所有航班滿足條件。
(2)重新搜集飛機的到達和起飛機場。
(3)采集航班延誤旅客人數、飛機折舊費、飛機停場費、起降費、旅客賠償費相關成本數據等。
(4)計算所有航班串的調整成本,建立目標函數。
(5)根據約束條件,將成本矩陣輸入Matlab軟件編程求解模型并繪制時空網絡圖。
(6)得到新航班調整策略與各航班串延誤成本,直至結果滿足實際要求。
3 算例分析
表2 是成都某航空公司一天內成都、北京、杭州三個機場的航班計劃,共包括14個航班、6架飛機、3個機場。因天氣條件低于機場最低飛行標準,管理部門決定在當天的6:00—9:00關閉成都機場,在此時段內機場不允許任何航空器起降,而此時段前的所有航班都可以正常起飛降落,此時段后機場立即允許飛機正常起飛降落。航班f8 因大霧低能見度,航班備降后機組超時而取消。
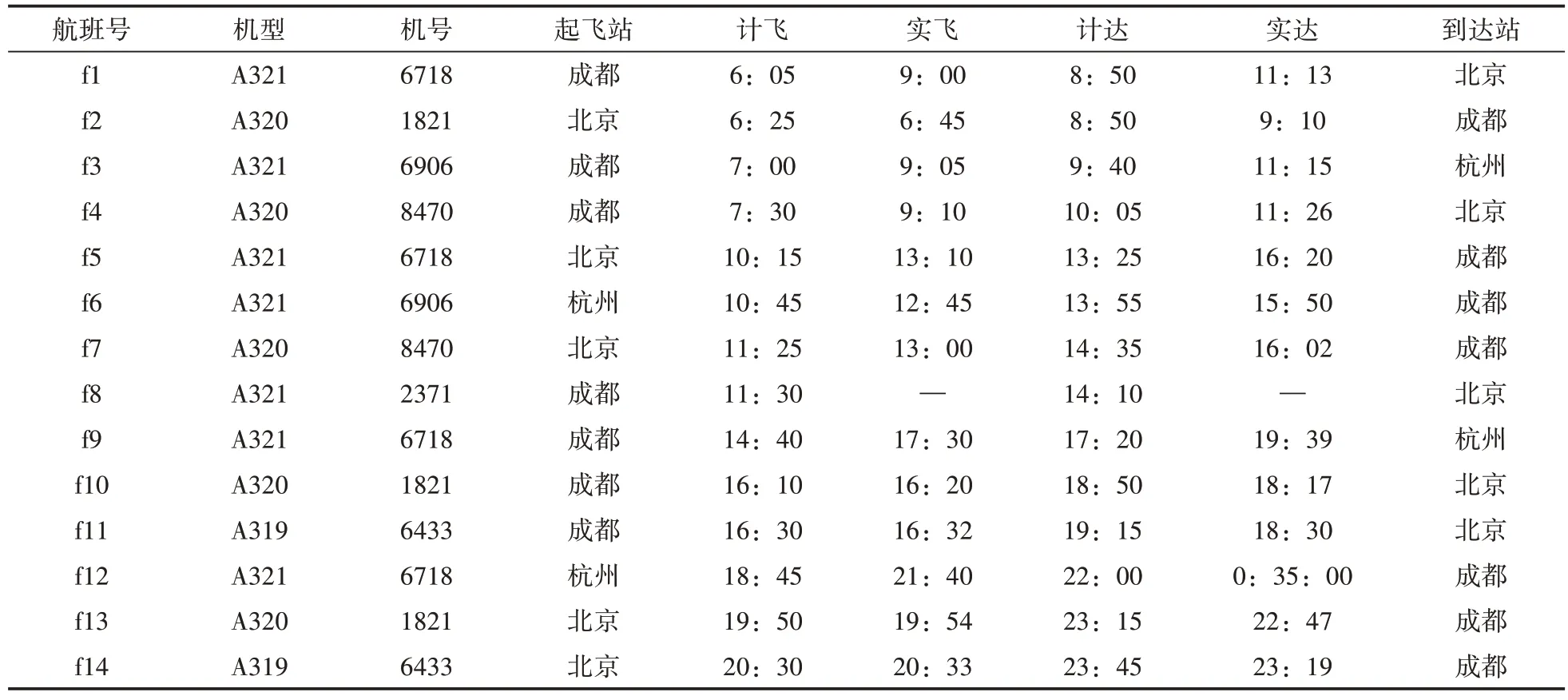
表2 原航班恢復計劃表
根據動態規劃算法,構造航班成本矩陣,計算出每個可行航班的成本,通過Matlab 軟件計算得到航班調整方案,為了避免太多無效航班串致使Matlab 求解速度太慢,規定前序航班與緊后航班之間不得超過8 h,所有航班間隔8 h以上的匹配均無效。將各機場成本矩陣輸入Matlab 進行編程來求得使各個機場成本最小的最優解矩陣,最后將三個機場的最優解矩陣進行整合,得出新航班調整計劃的航班串,并根據飛機起飛和到達機場、執行航班飛機的起飛機場來整合出已有的各架飛機所執行的新航班。Matlab 求解得到成都機場、北京機場和杭州機場的最優解矩陣依次見圖2、見圖3和圖4。

圖2 成都機場最優解矩陣
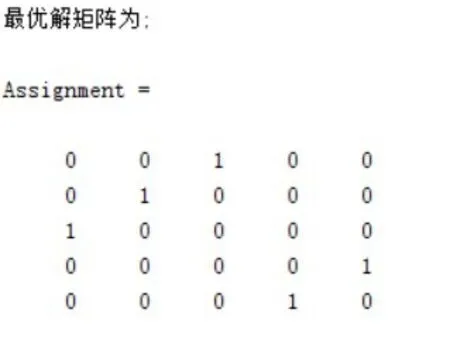
圖3 北京機場最優解矩陣

圖4 杭州機場最優解矩陣
根據成都、北京、杭州機場的最優解矩陣,得到新的航班恢復計劃表,見表3。
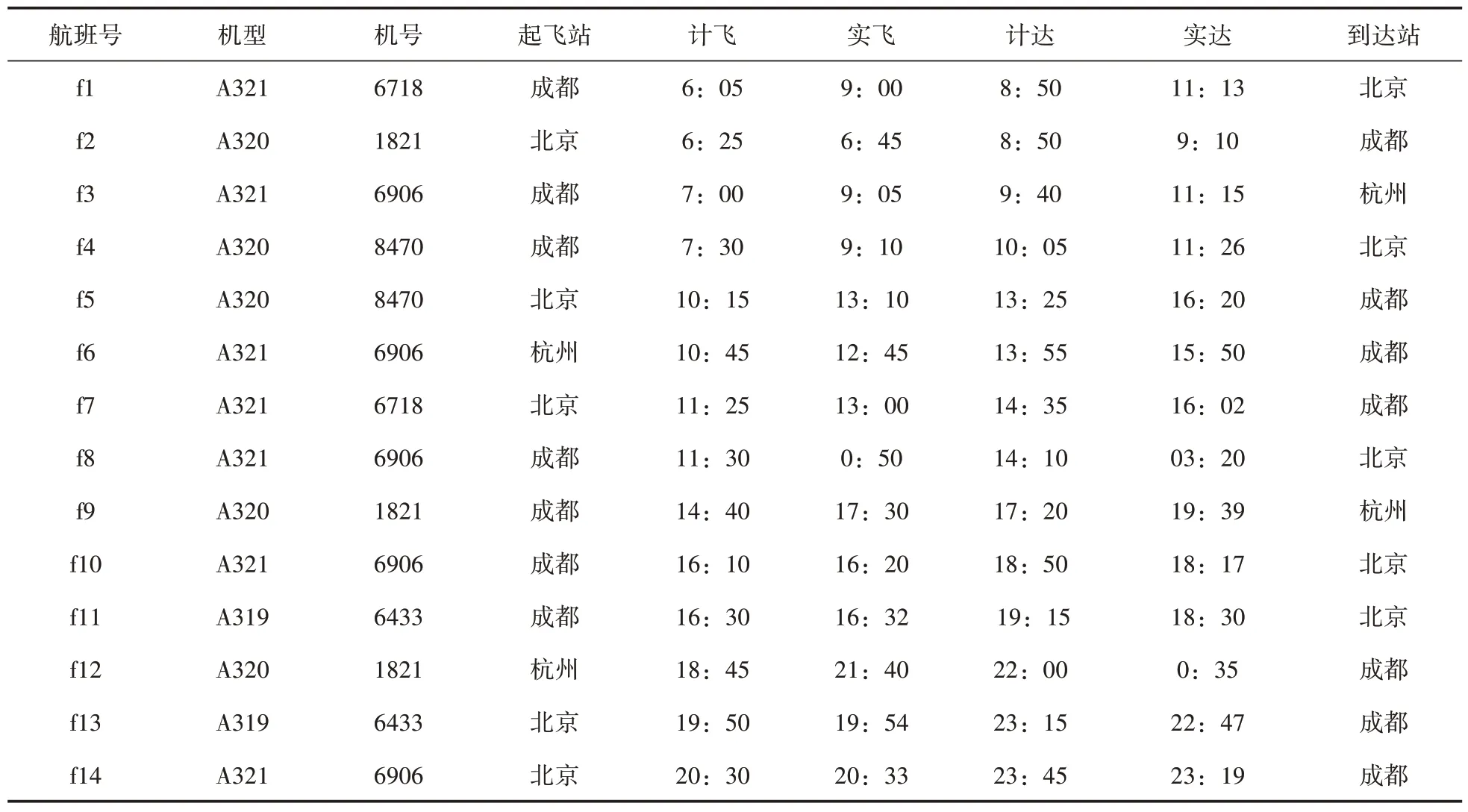
表3 新航班恢復計劃表
利用時空網絡圖對新航班計劃表進行描述,繪制出調整之后的各航班串,見圖5。實驗結果分析:原航班恢復計劃表表1 中,航班串為f1—f5—f9—f12,恢復成本10.11萬元,f2—f10—f13恢復成本20.14萬元,f3—f6恢復成本3.05,f4—f7 恢復成本3.5,f8 航班取消,成本58 萬元,f11—f14 恢復成本4.1 萬元,總最小成本目標函數值為95.4 萬元。新航班恢復計劃表表2 中,航班串為f1—f7,恢復成本3.7 萬元,f2—f9—f12,恢 復 成 本18.18 萬 元,f3—f6—f10—f14—f8,恢復成本32.63 萬元,f4—f5,恢復成本3.8 萬元,f11—f13,恢復成本2.3 萬元,總最小成本目標函數值為60.61 萬元。可見新航班恢復計劃成本比原航班恢復計劃成本降低36.5%。

圖5 恢復后航班時空網絡圖
4 結語
本文通過充分考慮航班恢復的實際背景,從不正常航班延誤成本最小化的角度出發,將可用航班的次序進行調整等方式,在指派模型的基礎上建立使不正常航班調整的成本最小化的目標函數,運用Matlab 軟件求解航班最優排班,盡可能使航空公司的經濟損失降到最低。本文建立的成本最小化模型及算法適應面廣,在短時間內能計算出使延誤成本最低的航班調整計劃,模型合理,算法較為準確,能提高簽派員工作效率,具有一定的研究價值和發展潛力。本文存在一定的可改進空間,也是下一步需要繼續研究的地方。比如:①航班調整方面僅考慮延誤成本,未考慮到旅客滿意度和公平性等問題。②沒有將成本指標和非成本指標賦權結合考慮,須在實踐中繼續研究,充分考慮實際,將非成本指標建立模糊綜合評價體系。③模型進行成本最小化求解時,是將三個機場分開,分別將每個機場同時作為前序航班的到達機場和后續航班的出發機場進行各最小調整成本求解,最后將三機場最小成本求和得到最小總成本,下一步可考慮直接求解所有機場的最小調整成本。

