數學大師的獨特視角

林革

陳省身（1911～2004）是美籍華裔當代著名數學家、中國科學院首批外籍院士，被稱為20世紀最偉大的幾何學家之一. 國際數學聯盟特別設立的“陳省身獎”是國際數學界最高級別的終身成就獎. 陳省身心系祖國，晚年致力于推進中國數學科學的發展，經常去高校和研究所講學，被譽為“中國年輕數學學子的總教練”.

1980 年，陳省身到北京大學做學術報告. 報告一開場他便出驚人之語：“人們常說三角形的內角和等于180°， 我認為這種說法不妥！”頓時全場嘩然，這個數學定論是連小學生都知道的常識，怎會錯誤？大家簡直不敢相信自己的耳朵，“真的假的？是陳教授口誤，還是自己聽錯了？”

這時，陳省身笑著擺擺手說道：“我說‘三角形的內角和等于180°’不妥，不是說這個事實是錯誤的，而是說人們看待這個結論的方式不對，實際應該說‘三角形的外角和等于360°. ” “既然三角形的內角和等于180°不錯，為何要強調外角和等于360°呢？”聽眾們不禁暗自嘀咕.

早有預料的陳省身解釋道：“數學中經常需要歸納總結一些規律，那么規律的普遍性就顯得尤為重要. 三角形的三個內角和是180°，雖然也是規律，但呈動態特征. 也就是說，推廣到多邊形的內角和就產生變化，比如：四邊形的內角和是 360°，五邊形的內角和是540°，六邊形的內角和是720°……n邊形的內角和是（n - 2）× 180°. 但是，稍加觀察大家就會直觀發現，三角形的外角和是（180° + 180° + 180°）- 180° = 360°，四邊形的外角和是（180° + 180° + 180° + 180°） - 360° = 360°，五邊形的外角和也是（180° + 180° + 180° + 180° + 180°） - 540° = 360°，六邊形的外角和仍是（180° + 180° + 180° + 180° + 180° + 180°） - 720° = 360°……可以歸納出，任意多邊形的外角和都是 360°. 這個結論不僅概括了所有情形，而且用一個與 n 無關的常數代替與 n 有關的計算公式，顯然更具一般性和普遍性. ”聽眾們這才恍悟驚人之語的話外之音.

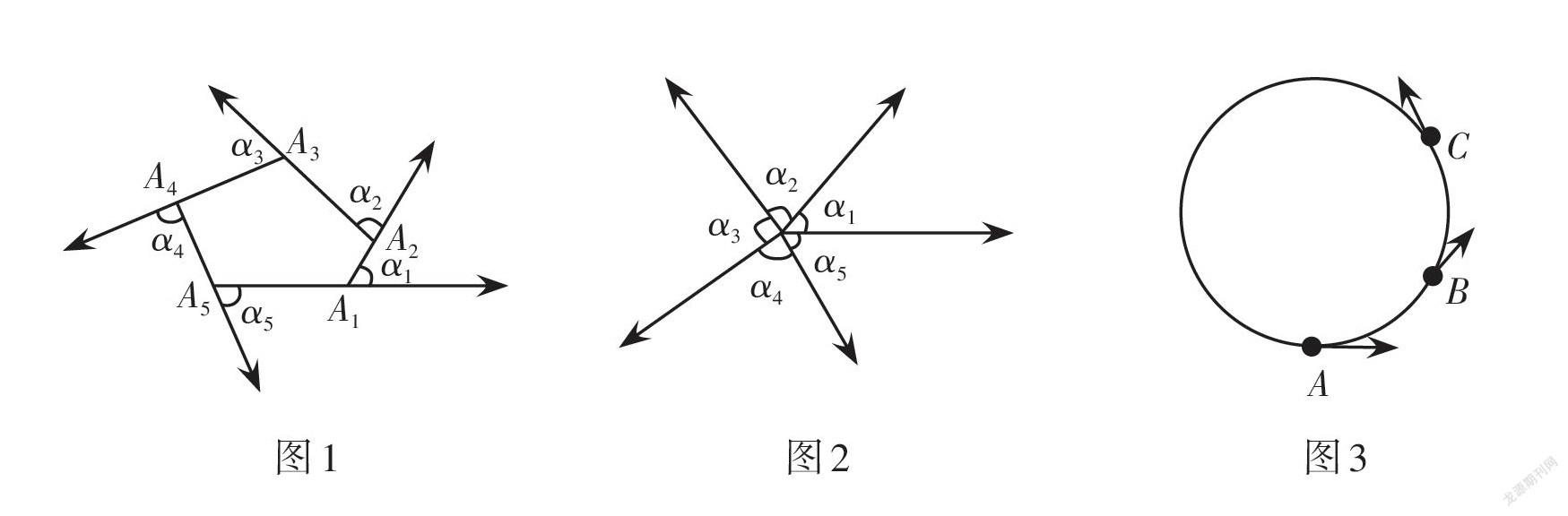
陳省身趁熱打鐵，隨手畫了張示意圖，繼續道：“這個靜態確定的規律，可以借用圖形直觀理解. 不妨假想一只螞蟻沿多邊形A1A2A3A4A5（如圖1）的邊界繞圈爬行，每次經過一個頂點時，它都要改變原本直行的方向，也就是轉過一個角度. 比如，開始從點A1出發時角度為α1，到了點A2就變成了α2，到了點A3就變成了α3……轉過的角度恰好是這個頂點處的外角度數. 爬了一圈轉回到點A1，角度改變量之和（如圖2）當然是一個周角360°，因此，多邊形的外角和為360°. ”

怎么樣？大師就是大師，想象奇特，眼光獨到，講解直白，分析通俗，果然令人耳目一新.

需要指出的是，陳省身一再強調的“外角和為360°”，此規則實際上適用于所有閉合曲線，只不過在表述時，要用“方向改變量”來代替多邊形的“外角和”而已. 最簡單、最極端的例子當然是圓周.

設想螞蟻沿著一個圓周爬行. 這時，它爬行的方向隨時隨地在改變. 譬如，開始時，螞蟻在點A處逆時針爬行. 它開始時面朝東，然后到點B再到點C，如此漸漸地面朝東北、北、西北……最后回到點A時，螞蟻又面朝東，所以它的方向改變量為360°（如圖3）.

1944年，陳省身找到了一般曲面上封閉曲線方向改變量總和的公式，這就是“高斯—比內—陳公式”，并在此基礎上發展出“陳氏類”理論. 這個理論在物理領域有極為重要的應用，被稱為劃時代的貢獻，而這個理論始于轉換視線——把注意力從內角和轉到外角和.

數學家波萊爾說：“數學家的目的往往是尋求一般的解，他喜歡用幾個一般的公式來解決許多特殊的問題. ”即從眾所周知的事實出發，變換角度換向思考，深入挖掘出更具普遍性的深刻規律. 當然，這需要透徹敏銳、獨特深刻的數學眼光和對真理窮追不舍、孜孜以求的執著精神，上面的小故事應該算是佐證.

（作者單位：揚州職業大學）