具有五階色散項(xiàng)的Van der Waals方程波前解的持續(xù)性

楊思源，傅仰耿

（華僑大學(xué)數(shù)學(xué)科學(xué)學(xué)院，福建 泉州 362021）

引 言

近年來，對(duì)由非彈性碰撞粒子所組成流體的研究引起了人們的廣泛關(guān)注。在流化粒狀的流化狀態(tài)中，粒狀物質(zhì)被連續(xù)的能量注入而流化，呈現(xiàn)出類分子流體傳播、圖形形成和相變等豐富的運(yùn)動(dòng)，引起了人們對(duì)這種類似于分子流體現(xiàn)象的關(guān)注。在這種情況下，Abourabia 等[1]認(rèn)為粒狀物質(zhì)的顆粒可視為類似于流體的分子，并試圖利用動(dòng)力學(xué)理論來描述介質(zhì)的行為。當(dāng)粒狀流動(dòng)在接近臨界點(diǎn)時(shí)，用Van der Waals 方程可以很好地描述相分離的流態(tài)化顆粒體系。而在準(zhǔn)聲速極限下，可以用兩個(gè)KDV方程來描述這種運(yùn)動(dòng)[2-3]。

Van der Waals方程如下所示：

該方程為物理學(xué)中非常重要的一類非線性偏微分方程[4]，其精確行波解在對(duì)這些方程的研究中起到了重要的作用，可以提供更多的信息來理解這些物理現(xiàn)象。這也促使學(xué)者們?yōu)榱双@得該方程的行波解而提出多種方法，例如雙曲正切函數(shù)法[5]、Painlevé 分析法[6-9]、Jacobi 橢圓方法[10-12]以及tanh 展開方法及各種推廣[13-14]。通過這些方法，已找到了一些行波解。例如2006年Marcel等[4]找到式(1)的精確孤立波解，并指出式(1)有兩個(gè)波前解，但沒有找到波前解的精確形式。

2015 年Abourabia 等[1]通過Painlevé 分析方法得到了式(1)的兩個(gè)波前解：

其中ξ=kx+ωt。

的情況下，用動(dòng)力系統(tǒng)理論與分支方法得到了式(1)的兩個(gè)波前解：

其中ξ=x+ct。

在行波理論中，行波解的存在性是一個(gè)基本問題。非線性發(fā)展方程的波前解與行波系統(tǒng)的異宿軌是相對(duì)應(yīng)的，所以通常將方程波前解的存在性轉(zhuǎn)化為相空間上異宿軌的存在性進(jìn)行研究。當(dāng)發(fā)展方程存在高階項(xiàng)時(shí)，相對(duì)應(yīng)行波系統(tǒng)的相空間是高維的，異宿軌存在性的研究通常非常困難。但在小參數(shù)情況下可以利用幾何奇異攝動(dòng)理論[16]降低相空間維數(shù)，進(jìn)而證明異宿軌的存在性，例如含有時(shí)空延遲的KPP 方程波前解的持續(xù)性[17]、Generalized Burger-Huxley方程波前解的持續(xù)性[18]等研究。

本文研究如下具有五階色散項(xiàng)的Van der Waals方程的波前解的存在性：

其中a、b、ε都是正常數(shù)，分別刻畫了有效粘度、與壓縮系數(shù)成正比的分叉參數(shù)和五階色散[19]的效果。利用動(dòng)力系統(tǒng)和幾何奇異攝動(dòng)理論證明了當(dāng)ε充分小時(shí)，式(2)的波前解是持續(xù)存在的。

1 動(dòng)力系統(tǒng)的刻畫

對(duì)式(2)進(jìn)行行波變換，也就是將u(x,t)=U(ξ),ξ=x-ct代入式(1)，并且積分兩次可以得到：

在式(3)中，積分常量為0。令U'=v、v'=w以及可以將式(3)改寫為：

當(dāng)c2-b> 0時(shí)，顯然系統(tǒng)(4)有3個(gè)平衡點(diǎn)：

接下來主要討論Y0和Y1。系統(tǒng)(4)在Y0處的線性化矩陣為：

對(duì)應(yīng)的特征方程為：

類似的，系統(tǒng)(4)在Y1處線性化矩陣為：

對(duì)應(yīng)的特征方程為：

從而有如下定理：

定理1如果c2-b> 0且c＜ 0，那么式(3)中Y0的不穩(wěn)定流形是一維的,Y1的穩(wěn)定流形也是一維的。

證明定理1 的證明是基于輻角原理得到的。式(5)所決定的是Y0附近線性化的譜，所以把式(5)進(jìn)行改寫，改寫后變成m0(λ) = 0，其中：

需要證明的是m0( )λ= 0 在右半復(fù)平面只有一個(gè)根。由于m0( )λ是解析函數(shù)，所以它在右半復(fù)平面的根的個(gè)數(shù)為：

其中周線c0作為半徑為R的有向邊界，其方向是逆時(shí)針的，中心是原點(diǎn)。?c0argm0(λ)代表m0(λ)的輻角沿著c0轉(zhuǎn)一圈的改變量。式(7)就成為1.5 +其中中括號(hào)里面的量表示當(dāng)R從∞到-∞時(shí)，輻角argm0(iR)的改變量。因此，上述問題轉(zhuǎn)化為計(jì)算m0(iR)的像繞著原點(diǎn)轉(zhuǎn)了多少圈。注意到：

其次考慮R從0 到-∞的情況，Rem1(iR)從(c2-b)單調(diào)遞減到-∞，Imm1(iR)從0 遞增到∞。當(dāng)，R2= 2(c2-b)，所 以，當(dāng)R從0 到-∞時(shí)，m1(iR)的像在復(fù)平面上從出發(fā)，方向逆時(shí)針，經(jīng)過第一象限，與虛軸交于( )0,y0，到達(dá)第二象限并停留在第二象限，有如下漸進(jìn)行為當(dāng)R→-∞時(shí)，同 理 可 得因此，式(5)在左半復(fù)平面根的個(gè)數(shù)也是1，定理1得證。

從定理1可以看出，當(dāng)相空間是三維時(shí)，穩(wěn)定流形Ws(Y0)的維數(shù)和不穩(wěn)定流形Wu(Y1)的維數(shù)之和是2。因此，在R3中Y0和Y1有可能會(huì)相交于一條一維的曲線，也就是系統(tǒng)(4)的一條異宿軌。下面運(yùn)用幾何奇異攝動(dòng)理論嚴(yán)格地證明相交的存在性。

2 小耗散波前解的存在性

這里考慮ε充分小的情形，來證明具有色散項(xiàng)的方程波前解的持續(xù)性。當(dāng)0ε?1 時(shí)，系統(tǒng)(4)可以改寫為如下形式：

令η=，則與系統(tǒng)(8)對(duì)應(yīng)的快系統(tǒng)為：

在系統(tǒng)(8)中令ε= 0，則U和v滿足下面這個(gè)系統(tǒng)：

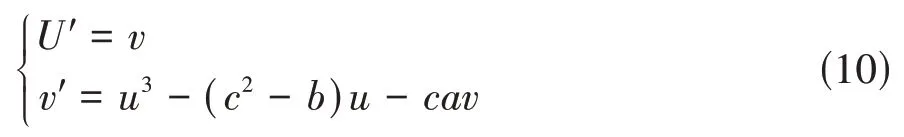
系統(tǒng)(8)中w限制在下面這個(gè)集合中：M0=易見M0是在R3中的一個(gè)二維子流形。根據(jù)文獻(xiàn)[15]中的定義可知，若限制在M0上的線性化快系統(tǒng)有M0維數(shù)個(gè)特征值在虛軸上，剩下的都是雙曲的，則稱流形M0為法向雙曲流形。限制在M0上的快系統(tǒng)(9)的線性化系統(tǒng)的矩陣如下：

計(jì)算可知這個(gè)矩陣的特征值為0、0、1，故M0為法向雙曲的。因此由Fenichel 穩(wěn)定流形理論可知：對(duì)于足夠小的ε> 0，有一個(gè)二維子流形Mε存在于R3中，使得它在M0的ε鄰域內(nèi)，并且對(duì)于系統(tǒng)(8)的流是不變的。

為了確定Mε上的動(dòng)力學(xué)行為，記：

其中g(shù)(U,v,ε)光滑依賴于ε并且滿足g(U,v,ε)= 0。把式(11)中w的表達(dá)式代入系統(tǒng)(8)的第三個(gè)方程，得到：

再在ε處將g(U,v,ε)進(jìn)行泰勒展開，可以得到：

將g(U,v,ε)代入式(12)并且比較ε同階項(xiàng)的系數(shù)。ε零次冪的系數(shù)為g(U,v,0) = 0；比較ε的一次冪的系數(shù)：

這樣將系統(tǒng)（8）改寫為：

式(13)決定了Mε上的動(dòng)力學(xué)行為。

下面將給出持續(xù)性定理并證明。

定理2如果方程utt+(uxx-aut-u3-bu)xx=0 存在一個(gè)嚴(yán)格遞增的波前解u0(x,t) =U0(ξ)，并且滿足那么對(duì)于足夠小的ε> 0，式(2)的波前解持續(xù)存在，即對(duì)具有五階色散項(xiàng)的式(2) 也存在一個(gè)波前解u(x,t) =U(ξ)，并 且 滿 足

證明當(dāng)ε= 0 時(shí)，系統(tǒng)(10)有波前解U0(ξ)，其對(duì)應(yīng)的異宿軌連接平衡點(diǎn)Y0和Y1。

對(duì)于充分小的ε> 0，容易驗(yàn)證Y0和Y1也同樣是系統(tǒng)(11)的平衡點(diǎn)。下面證明系統(tǒng)(11)也存在異宿軌將Y0與Y1連接起來。將式(12)改寫為如下形式：

其中Φ(U,v,c,ε)滿足Φ(U,v,c,0) =u3-(c2-b)u-cav。

故U0(ξ)是嚴(yán)格遞增的，從而可以被刻畫成為某個(gè)函數(shù)的圖像，把該函數(shù)表示為v=f(U,c0)。通過穩(wěn)定流形理論知，對(duì)于充分小的ε> 0，Y0的不穩(wěn)定流形可以被函數(shù)v=f1(U,c,ε)的圖像刻畫出來，其中f1(0,c0,0) = 0。由解對(duì)參數(shù)的連續(xù)依賴性定理可知，當(dāng)ε充分小時(shí)，此流形一定過直線上的某一點(diǎn)。類似的，在Y1處的穩(wěn)定流形用v=f2(U,c,ε)來進(jìn)行刻畫。顯然有f2(,c,ε) = 0，這個(gè)流形在ε充分小的情況下，一定也過直線U=上的某一點(diǎn)。由于

因此，要證明式(14)在ε> 0 時(shí)存在一條異宿軌，只需證明在c0的附近存在唯一的函數(shù)c=c(ε)，使流形f1和f2在直線上相交于同一個(gè)點(diǎn)即可。定義函數(shù)：

注意到v=f1(U,c,ε)和v=f2(U,c,ε)全都滿足下面這個(gè)方程：

故

因此：

同理可得：

因?yàn)閁0(ξ)嚴(yán)格遞增,所以對(duì)任意的0U都有f(U,c0)＜ 0存在。于是有：

因此由隱函數(shù)定理知，對(duì)于充分小的ε> 0，G(c,ε) = 0 在c0附近存在唯一的解c=c(ε)。由此證明了在直線U=上流形f1和流形f2有一個(gè)交點(diǎn)，也就是說系統(tǒng)(13)存在一條連接Y0和Y1的異 宿 軌。 即 式(1) 存 在 滿 足ξl→im-∞U0(ξ) = 0，的波前解。

3 數(shù)值模擬

現(xiàn)在數(shù)值模擬五階Van der walls 方程的波前解。取顯然要找系統(tǒng)(13)的解u(ξ)滿足邊界條件：

考慮由式(13)和式(22)組成的在有限區(qū)間[L1,L2]上的邊界問題，要求當(dāng)L1→-∞和L2→∞時(shí)，近似解收斂到一個(gè)實(shí)際解[20-21]。根據(jù)文獻(xiàn)[22]中的方法，要求解于ξ=L1處在Y0的穩(wěn)定流形和于ξ=L2處在Y1的不穩(wěn)定流形都沒有投射。易知因此為了解決這個(gè)問題，還必須增加一個(gè)條件。由于系統(tǒng)(13)的平 移 不 變 性 以 及 觀 察 到u(ξ)從0 增 加 到1，故u( 0 )= 0.5。

關(guān)于求常微分方程邊值問題的數(shù)值解，Matlab提供了一個(gè)有效方法[23]，即利用程序bvp4c 使用配置方法并要求提供一個(gè)近似解，用

作為近似解，其數(shù)值模擬如圖1所示，其中相對(duì)容忍誤差為10-3，絕對(duì)容忍誤差為10-6。

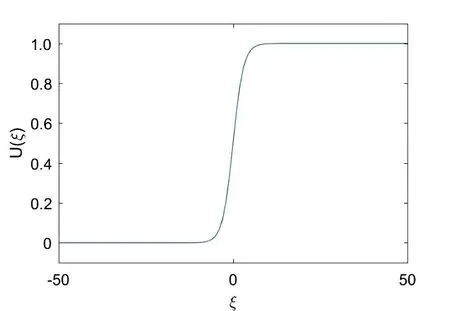
圖1 五階Van der Waals方程的近似解

4 結(jié)束語(yǔ)

本文研究具有五階色散Van der Waals 方程波前解的持續(xù)存在性，利用動(dòng)力系統(tǒng)與幾何奇異攝動(dòng)理論，證明在充分小色散情況下，其波前解是持續(xù)存在的。值得注意的是幾何奇異攝動(dòng)理論是抽象的、嚴(yán)格的且不需要未擾動(dòng)系統(tǒng)波前解的精確表達(dá)式，能把高維相空間問題轉(zhuǎn)化為低維問題，從而大大降低了難度。目前，對(duì)于高價(jià)偏微分方程波前解的存在性，幾何奇異攝動(dòng)理論已是一重要方法。本文的結(jié)果豐富和推廣了前人的研究成果，具有一定的理論意義。