小學低年段數學解決問題的教學難點與對策

梁慶鋒

【摘要】小學低年段數學解決問題的教學難點直接影響學生的學習效果。本文從學生的視角和教師的視角分析小學低年段解決問題教學過程中的難點，教師可從協助學生獲得讀懂題目、分析問題、擬定計劃的方法進行突破，實現高效教育教學的目的。

【關鍵詞】小學低年段;數學解決問題;教學難點

突破策略教學難點，顧名思義就是在教學過程中大部分學生難以理解、不易理解的知識點。一般情況下，教學重點在教材編排中是顯而易見的，教師容易“吃得透、抓得準”。但教學難點在教材編排中有時候則有著較強的隱蔽性。數學解決問題既要聯系實際，也要突出數學方法，最能反映學生的邏輯思維。新課程改革以來，數學解決問題得到了前所未有的重視，成為我國數學教育教學的重點、難點，同時也是薄弱環節。下面，筆者結合小學二年級數學教學實踐，對解決問題的難點進行解析，根據對應的問題開展相關的教學策略。

一、抓準解決問題教學的難點

學生學會分析問題的基本方法和解決問題的整體思路，避免憑直覺做題是小學低年段突破解決問題教學的難點。在解決問題的教學中，經常可以遇到一些看似好笑又令人費解的錯誤，例如：

錯例一：有2束菊花，一束有8朵，一束有7朵，一共有多少朵菊花？2+8+7=17（朵）。

錯例二：動物園準備8個籠子養小白兔，先買來24只兔子，再買來16只兔子，平均每個籠子放幾只兔子？24÷8=3（個）或 24÷8=3（個），3+16=19（個）。

學生在解答問題的時候，不知從何入手，或者思路紊亂，這些難點令教師最為頭疼。“都已經交代清楚了，為什么學生還會出錯？”“題目稍微改動一下，學生為什么就想不出來呢？” “學生根本不看題，就是拿兩個數隨便加減乘除，隨便碰一碰。”這些充滿疑問且無奈的話，道出了部分教師的心聲。

在解決問題教學過程中，教師看似已經把教的東西都交代清楚了，甚至把重難點重復講了好幾遍，但學生對知識的理解掌握卻還是沒有達到預期的目的，學習的質量也沒有達到預期的效果。究其原因，主要是教師在教學過程中，沒有幫助學生有效的獲得解決問題的分析能力和解題方法，學生也不知從何入手，也就是沒有真正突破教學難點造成的后果。

二、有效突破解決問題教學難點的策略

筆者結合具體教學實踐，通過對“學生是怎樣解決數學的解決問題？”“教師應該如何協助學生解決數學解決問題？”的研究，總結以下突破解決問題教學難點的策略，促進學生思維完成階段性的飛躍。

（一）協助學生獲得讀懂題目的方法

協助學生獲得讀懂題目的方法，也就是對低年段學生審題能力的培養，使學生能正確理解題目要求，強化對數學語言的運用于理解。低年段學生審題能力較弱，習慣使用生活語言對事情進行描述，主要原因是學生識字量有限，審題經驗尚淺。這就需要教師有意識培養學生的審題能力，并把它確立為每節課的教學目標之一，可以從以下三點堅持訓練：

1.抓中心事件，收集條件。教師可以教學生從問題出發，例如，前面所舉的“錯例一：有2束菊花，一束有8朵，一束有7朵，一共有多少朵菊花？”中，引導學生抓準題目的問題是“求一共有多少朵菊花？”從問題出發，獲得題目講的是求菊花的朵數，然后收集與朵數相關的條件“一束有8朵”“一束有7朵”，與“有2束菊花”無關，排除多余的條件。抓中心事件收集條件的方法能幫助學生準確、快速地判斷出“題目求的是什么？已知什么？”關鍵是讓學生知道在解決問題的時從何入手。

2.抓題目中的關鍵句。關鍵句是反映題目數量之間的關系的句子，在教學過程中有著重要的作用，直接影響學生對題目的理解。如，“一班得了12面小紅旗，二班比一班多得3面。二班得了多少面？”的例題中，“二班比一班多得3面”這句話中反映了“一班”和“二班”兩個數量比較的關系，從這個關鍵句中還知道是以“一班”的數量為標準，而且已知它的數量是12面。“求二班的紅旗面數”就是“求比12多3是多少？”像這樣，教師需要協助學生獲得讀懂題目中關鍵句的方法，以確保快速正確理解題目意思和數量關系。

3.梳理類型，形成網絡。梳理類型一般安排在一個單元和一個學期的末尾，例如，小學二年級數學上學期，就可以整理出加法、減法、乘法、連續兩問、求一個數比另一個數多（少）多少、乘加乘減、判斷夠不夠這7種不同類型的解決問題。對所學的解決問題進行歸納總結，有利于學生進行對比溝通，區分異同，升華規律，舉一反三，形成網絡，以達到加快學生審題的反應速度和判斷思路。

（二）協助學生獲得分析問題的方法

協助學生學會深入分析題目表達意思的方法，是小學數學解決問題的教學重點，也是難點。低年段學生的思維尚處于直觀的動作感知水平，能操作能理解、不能操作憑直覺是學生分析題目的最大特點。能夠操作，能夠看得見，學生就容易理解，不能操作，只是憑文字，又看不到圖，學生較多的時候就是憑直覺判斷。

例如，在教學中，如下圖一，一捆一捆的胡蘿卜是具體的事物，學生不僅能看到它，而且可以數，也就是能操作它，學生可以通過“動作”知道題目求4個5的和是多少？可以用4×5來計算。假如把這題換成下圖二這樣的文字題，這題到底是求4個5還是5個4的和？這時候學生會一片混亂。因為沒有了圖，學生不能數，缺少了具體的事物，學生不會主動去尋找可操作的工具。于是，學生的思維就會退回較低的認知水平：憑直覺判斷求幾個幾的和。

由此看出，交給學生一種可操作的分析方法（如，畫圖、數數等）是突破低年段解決問題教學難點的關鍵。給予學生操作，學生自然會覺得簡單，準確率也會高很多。當碰到一道解決問題是全文字的題目時，教師協助學生讀懂題目之后，讓學生學會用圖畫表示題目中的數量關系，如，下圖三中是其中的兩種畫圖方法，只要學生能操作能理解就可以。畫圖的目的是為了通過看圖抽象數理。因為畫圖能輔助學生理解題目中的數量關系，學生通過看圖，通過數數操作，能抽象出數理：求4個5的和是多少？只要學生的圖能畫對，數理的表述基本都會準確，最后就能列出正確的算術解答。

具體分析流程如下圖四所示，在面對抽象文字題時，教師要幫助學生構建一個具體的分析流程，這四個步驟告訴學生在審題之后，不是馬上就列式解答，還需要用畫圖表示題目中的數量關系。而畫圖表示題目中的數量關系的目的是為了抽象數理。題目是千變萬化的，唯獨數量關系是有規律可循的。也正是不斷從畫圖強化提煉題目中的數量關系，看圖強化抽象數理的能力，學生的思維才能有質的提升，學生方可獲得解決問題的方法。以不變應萬變，做到心中有依有據，不因題目的變化而害怕，學生學得靈、學得活。大部分憑直覺做題的學生正是因為從第一步直接跳到第四步，缺少了中間分析數量關系，抽象數理的環節，是經不起日后學習考驗的。

（三）協助學生獲得擬定計劃的方法

當遇到兩步或者兩步以上的解決問題時，擬定計劃是一個非常重要的解題策略，但是這一步驟卻容易被教師忽略，這正是造成學生解題思路缺失的原因之一。數學教育家波利亞在《怎樣解題》中提出解題的程序有：理解題目、擬定計劃、執行方案、回顧解答四個步驟。關于擬定計劃的介紹，首先是找到已知數據與未知數量之間的聯系。如果找不到聯系，就需要考慮引入某個輔助的元素（中間問題）。然后回憶一道與它相關的題目，而且以前解答過的。最終，便能得到一個解題的思路，擬定一個解題的方案。

例如，在前面所舉的錯例二中，學生的兩種錯例皆是因為學生缺乏一個整體的解題計劃，沒有尋找到題目的中間問題——兔子的總只數，使得學生憑自己熟悉的知識經驗、解題經驗去解決問題，也就是學生憑直覺解決問題。造成以上情況的主要原因是教師在教學過程中把解題計劃分割，課堂上，教師告訴學生第一步要做什么，然后學生跟著做，第二步要做什么，學生又跟著做，第三步……每一步學生都按照教師的要求去做了，學生卻不知道做了什么，缺乏對解題思路的整體認識。教師把解題思路這一難點全給包攬了，學生卻沒有得到這一方面的有效訓練。這樣的教學，最終結果是解題思路永遠在教師的心目中而不在學生的心中。沒有學會擬定完整的解題思路解決問題的學生，在遇到有中間問題的情況下，就會思路中斷或者混亂，不知從何做起，最后只能憑直覺解答了。

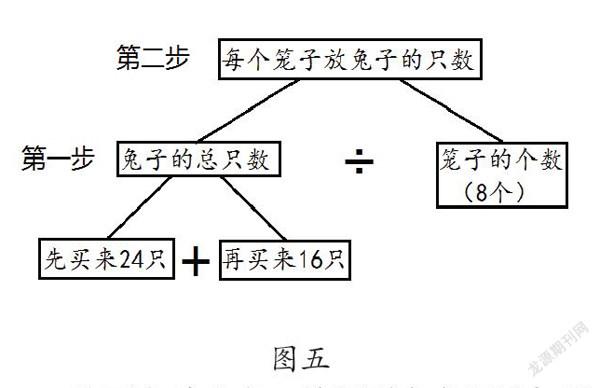
在平時教學過程中，教師需要讓學生意識到，擬定解題計劃對于能正確解題是非常重要的。其次，教師需要協助學生獲得擬定解題方案的方法。如下圖五所示，教會學生最好的方法是從問題出發。要求平均每個籠子放多少只兔子，需要知道兩個條件，分別是兔子的總只數和籠子的個數。把兔子的總只數去平均分，籠子有8個也就是把兔子的總只數除以8。要注意的是，兔子的總只數是指兔子所有的只數，兔子的總只數不知道，但題目給出先買來24只，再買來16只，可以把這兩部分合起來就可以求出總只數。這時候，把所有數量之間的邏輯關系分析清楚了，接下來要弄清楚，第一步先算兔子的總只數，第二步再算平均每個籠子放兔子的只數。

為了突破難點，教師要有意識地加強擬定解題方案的訓練：先算什么，再算什么，最后做什么才能解答問題。讓學生清楚知道，解答過程一共有幾個步驟，已經做到哪一步？還差哪一步？例題能讓學生復述解題的計劃，練習中也有利于讓學生養成先有解題計劃再做題的習慣。在教學實踐中，教師要有意識地向學生滲透解題過程的整體意識，讓學生感受到擬定解題計劃的重要性。

三、結語

在教學中，實現難點突破被視作是教學達標的重要因素，也是提高教學質量的首要任務。教師要有抓準教學中難點的能力，除了從教學內容上去分析，還要學會從學生的視角、教師的視角去分析，采取靈活有效的策略，才能真正有效地突破難點，切實提高教與學的質量。

參考文獻：

[1]鮑銀霞.促進學生有效學習的理念與策略[M].廣東高等教育出版社，2015.

[2]林夏雨.有效突破教學難點的策略例談[J].教學管理與教育研究，2020（22）.

[3]陳啟毅.小學數學低年級解決問題易錯題成因及對策[J].新課程（小學），2019（12）.