板結構中聲學黑洞參數優化及其陣列的能量匯集效應分析

梁浩鳴，高 康，劉獻棟，鮑 岳，單穎春，何 田

（北京航空航天大學 交通科學與工程學院，北京 100191）

聲學黑洞（Acoustic black hole，ABH）作為一種新型的波操縱方法，為結構的振動噪聲控制提供了新方法[1]。1988年Mironov[2]首先提出特定結構內存在聲學黑洞效應，即在一個厚度以特定的冪律形式變化的板內彎曲波波速會隨著厚度的減小而減小，在理想情況下（厚度減小為0），可實現彎曲波的零反射。即使該楔形結構的末端存在一定殘余厚度，該結構也能實現能量的匯聚，而在聲學黑洞結構的高能量密度區域粘貼上少量阻尼材料可實現高效的能量消耗，從而達到減振降噪的目的[3–4]。由于其具有高效、輕量化和寬頻等特性，備受科研人員關注。目前，對于聲學黑洞在振動噪聲控制的實際應用方面的研究涉及到汽車的底板[5]、發動機罩[6]和直升機駕駛艙等[7]。

聲學黑洞結構主要分為一維聲學黑洞和二維聲學黑洞兩種形式。對于板結構而言，二維聲學黑洞結構應用范圍更廣、更具研究價值。在此領域人們進行了大量研究。Yan 等[8]通過數值方法和試驗方法研究了蘭姆波在二維聲學黑洞結構中的傳播，結果表明初始傳播方向未指向聲學黑洞中心的波會向著中心方向偏轉，在理想情況下波速在中心位置降為零從而實現能量的匯聚。O’Boy 等[9]利用近似解析方法，對內嵌二維聲學黑洞的圓形板進行了頻響特性分析，并與不含聲學黑洞的板結構進行了比較，同時研究了阻尼材料的影響。Huang 等[10]應用幾何聲學的程函方程，通過數值積分方法研究了二維聲學黑洞對彎曲波傳播方向的影響，得到了聲學黑洞中彎曲波能量的匯聚過程和特性，為揭示聲學黑洞的工作機理提供了基礎。對汽車而言，車內高頻噪聲一般可以通過布置吸聲材料實現有效控制，而這些吸聲材料對于車身板件振動而產生的中低頻噪聲抑制能力不足；通過在車身板件上粘貼阻尼材料，使用阻尼減振原理減小板件振動進而降低車內噪聲，也是抑制車內噪聲的有效方法，但這增加了結構的重量和成本。在汽車結構輕量化背景下，汽車車身板件的設計既要考慮中低頻振動噪聲控制又要實現質量的減輕，而內嵌單個聲學黑洞的板結構難以在低頻段發揮作用[11]，因此需要研究多個二維聲學黑洞組成的聲學黑洞陣列，同時為了獲得更好的減振降噪效果，應在每個聲學黑洞中心高能量密度區域粘貼阻尼材料。

對于由多個二維聲學黑洞組合而成的聲學黑洞陣列這樣的復雜聲學黑洞結構，難以從理論上求得解析解，因此一般通過實驗或者有限元等數值仿真方法進行研究。在二維聲學黑洞陣列研究領域，研究者們也完成了許多工作。Conlon等[12–13]通過實驗的方法同時分析了25個、13個呈周期陣列形式內嵌二維聲學黑洞板結構以及無內嵌聲學黑洞的均勻板結構在粘貼阻尼材料下的聲輻射，研究了內嵌二維聲學黑洞陣列板結構在有效操控頻帶內及低于有效操控頻帶下限頻率范圍內的減振降噪效果。Jia等[14]通過在聲學黑洞線性陣列中分別粘貼阻尼材料和動力吸振器，并對比其在相同激勵下板內平均振動速度等，提出了將動力吸振器替代阻尼材料以進一步提升聲學黑洞陣列尤其是低頻下的能量匯集特性的新方法。何璞等[15]將聲學黑洞阻尼振子附加到傳統盒式結構中，通過有限元法和試驗研究了其動態性能，結果表明附加聲學黑洞阻尼振子的盒式結構具有高效能量匯聚和耗散能力。王小東等[7]提出了基于ABH 效應的內嵌式和附加式兩種減振降噪設計方案，通過有限元法分析了優化設計前后直升機駕駛艙模型的聲振特性，并搭建試驗平臺進行驗證，結果表明該設計方案不但能夠實現噪聲寬頻控制，還降低了系統的總質量。

目前，對于聲學黑洞陣列的研究相對較少，且未見聲學黑洞陣列中黑洞單元的排列方式對整個板結構的能量匯聚效果影響的研究報導；同時，現有二維聲學黑洞研究中用于加工黑洞結構的板厚一般5 mm 左右，而如此厚的板件在汽車車身幾乎沒有應用。基于以上考慮，本文利用有限元法，對于內嵌于較薄的板結構二維聲學黑洞和兩個聲學黑洞組成的陣列結構進行研究。首先，研究黑洞結構的幾何參數對聲學黑洞性能的影響規律，并找出聲學黑洞的最優幾何構型；其次，以該參數作為陣列中每個黑洞單元的幾何參數，研究汽車工程領域較為關注的頻帶200 Hz～1 800 Hz內不同排列方式陣列結構的能量匯聚效果。研究結論可以為聲學黑洞陣列的設計和聲學黑洞在汽車中的應用提供參考。

1 單聲學黑洞結構的設計

1.1 聲學黑洞效應的機理

典型的一維聲學黑洞結構如圖1所示[16]，在沿x軸方向即厚度增加的方向上，結構的厚度以冪函數形式h(x)=εxm變化，其中冪指數m≥2。若該楔形結構厚度沿x 軸負方向減小為零，此時的聲學黑洞結構稱為理想的一維聲學黑洞結構。

圖1 典型的一維聲學黑洞結構

對于一維聲學黑洞薄板，它的厚度僅與x坐標有關，其彎曲波控制方程可以表示為[17]：

其中：w是薄板的撓度，D(x)是局部彎曲剛度，D(x)=Eh3(x)/12(1-μ2)，E是彈性模量，μ是材料的泊松比，ρ是材料的密度，ω是圓頻率。

利用幾何聲學近似法，在x處橫向位移w(x)可以表示為如下的復數形式[16]：

其中：A(x)和φ(x,y)=φ′(x,y)βy/kp分別表示緩慢變化的幅值和準平面波的程函，kp為板中準縱波的波數，β是波矢在y軸的投影，在波垂直入射的情況下，β=0。將式(2)代入方程(1)，要使得等式成立，需要等式左邊的實部和虛部必須同時等于零，令實部為零并且省略關于A(x)和φ(x,y)的高階導數項，可以得到彎曲波程函方程：

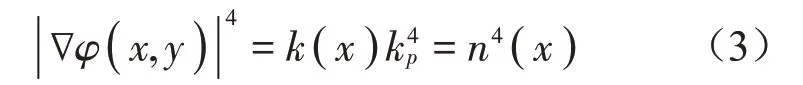
其中：k(x)=121/4k1p/4=[h(x)]-1/2，是薄板變厚度部分的局部波數，kp=ω/cp，h(x)是對應的反射系數。

對于彎曲波垂直入射的情況，由于波從楔形結構的任意一點x到楔形邊緣(x)=0 的傳播，產生的累積相位Φ可表示為積分表達式[16]：

可知當冪指數m≥2 時，式（4）發散，這意味著累積相位Φ會變為無窮大，波永遠不會傳播到楔形邊緣，所以也不會被反射回來，即波被“捕獲”。

但是實際上聲學黑洞結構的厚度不可能降為零，在加工制造聲學黑洞結構的過程中，受限于加工精度，必定會產生截斷，即聲學黑洞結構存在一定殘余厚度。研究表明[2]，即使是存在很小的殘余厚度，聲學黑洞結構的能量匯集效應也會受到較大影響。而Krylov 等[3]指出，在非理想聲學黑洞結構上粘貼阻尼材料即可降低反射系數，仍能獲得較好的減振效果。

將理想的一維聲學黑洞的截面繞其尖端位置所在軸線旋轉一周即可得到理想的二維聲學黑洞結構。同樣地，實際上二維聲學黑洞結構也存在殘余厚度，即非完美的二維聲學黑洞結構，它的示意圖如圖2所示。殘余厚度的存在會增加彎曲波的反射系數[2]，從而對二維聲學黑洞結構的能量匯集效應產生一定影響。

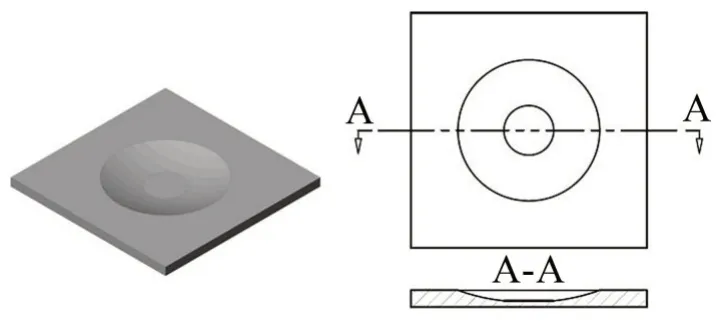
圖2 非完美二維聲學黑洞結構

1.2 正交試驗法優化單二維聲學黑洞

如圖3所示，內嵌單個二維聲學黑洞結構截面厚度與半徑關系可以表示為：

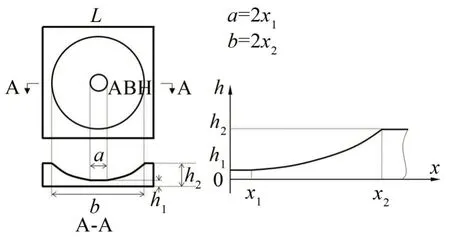
圖3 單二維聲學黑洞結構示意圖

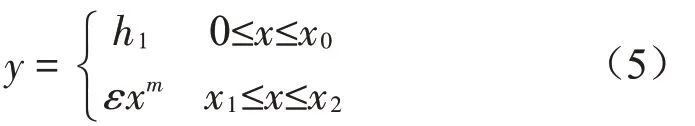
其中：x表示二維聲學黑洞結構內任意一圓截面的半徑；x1和x2分別表示黑洞結構內邊界及外邊界圓截面半徑；y表示二維聲學黑洞結構內任意一圓截面的半徑所對應的截面厚度，其中h1表示殘余厚度，h2表示板均勻部分的厚度，m表示冪指數，ε為系數。

由式(5)可知，殘余厚度h1，冪指數m和由系數ε決定的二維聲學黑洞結構外邊界半徑x2直接影響二維聲學黑洞結構的構型，也就是說這三個參數會改變內嵌二維聲學黑洞的板結構中振動能量的匯集，進而影響粘貼阻尼材料后的能量耗散效應。考慮到聲學黑洞結構有限元模型計算緩慢，為了快速分析上述參數對聲學黑洞性能的影響規律，選取殘余厚度h1（因素A）、冪指數m（因素B）和聲學黑洞外半徑x2（因素C）作為正交試驗的影響因子，每個因素取3個水平，進行3 因素3 水平的正交試驗，為單個二維聲學黑洞的優化設計提供參考。

本文將聲學黑洞內嵌于厚度為2 mm 的鋁合金薄板進行相關研究，該厚度鋁合金板在鋁制汽車車身上應用較多。矩形鋁合金薄板的幾何參數為400 mm×600 mm×2 mm，材料參數如表1所示。二維聲學黑洞結構的中心位置在平板的寬度方向居中，長度方向距離左端邊界400 mm；板的左邊界固支，其他邊界自由；激振力大小設為1 N，垂直于板面，作用在板結構寬度方向上的中心、長度方向上距左端邊界30 mm處，如圖4所示。考慮到板結構的尺寸，本文中選取殘余厚度h1（因素A）的3個水平分別為0.1 mm、0.15 mm和0.2 mm；冪指數m（因素B）的3個水平分別為2.2、2.4和2.6；聲學黑洞外半徑x2（因素C）的3 個水平分別為75 mm、85 mm 和95 mm，將相關數據填入正交試驗表進行正交試驗。正交試驗表如表2所示。

表1 鋁合金薄板材料參數

圖4 用于聲學黑洞優化的薄板結構

對表2所示的共9 組參數選取方案，分別在Solidworks、Hypermesh 和ABAQUS 建立幾何模型和有限元模型。為了比較上述二維聲學黑洞板在汽車工程領域較為關注的頻帶200 Hz～1 800 Hz內能量匯聚能力，使用ABAQUS軟件在該頻段內進行穩態動力學分析。

聲學黑洞結構高能量密度區域的振幅較大，在該區域粘貼相對少量的阻尼材料便可實現高效的能量消耗[3–4]。聲學黑洞結構匯聚的能量越多，高能量密度區域的振幅越大，越有利于阻尼材料的集中利用。所以，本文將能量匯聚效果作為評價聲學黑洞結構或陣列結構好壞的指標。為定量描述聲學黑洞匯集能量的效果，首先根據有限元仿真結果計算所關注頻段內每個激振頻率下聲學黑洞底部中心平臺內全部節點的垂直于板面方向的空間均方速度，即：

式中：vn為中心均勻厚度平臺某點的法向速度，v*n是法向速度的共軛；S是中心平臺的面積。

作為參考，計算均勻板在相同激振力和邊界條件下的響應。根據有限元計算結果，得到試驗號為1對應的聲學黑洞板中心平臺和均勻板相同位置的空間均方速度，它們在一定頻段內的分布如圖5所示。其中縱坐標用對數表示，參考值為1m2/s2。

圖5 空間均方速度對比圖

從圖5可以看出，均勻板的空間均方速度的峰值均在-30 dB～-8 dB范圍內，而二維聲學黑洞板的中心平臺內的空間均方速度峰值在-12 dB～11 dB之間，且ABH 板出現的峰值明顯多于均勻板。在277 Hz 以上的頻段內，聲學黑洞板結構的速度級在共振頻率處均有10 dB～30 dB 的增加，這表明振動能量發生明顯匯聚。為比較不同幾何參數下的聲學黑洞板在某一頻段內的能量匯聚效果，計算9 種聲學黑洞板在頻段200 Hz～1 800 Hz內的空間均方速度的平均值，所得結果如表3所示。

表3 試驗結果/10-2( m2 ?s-2)

根據表3所得結果，利用極差分析法[17]進行分析，結果如表4所示。其中Kjm為第j列因素m水平所對應的實驗指標和為Kjm的平均值，由的大小可以判斷j因素的優水平和各因素的最優組合；Rj為第j列因素對應值的極差，其反映第j列因素水平波動時，試驗指標的變動幅度。

表4 極差分析表/10-2( m2 ?s-2)

由表4可知，R1>R3>R2，這說明因素A 殘余厚度對試驗指標的影響最大，C 因素聲學黑洞外半徑次之，B 因素冪指數影響最小。由于試驗指標越大表示該聲學黑洞板的能量匯聚效果越好，本文中所選參數的最優組合為A1B1C2，即聲學黑洞板的殘余厚度取0.1 mm，冪指數取2.2，外半徑取85 mm。本文特定激勵條件、邊界條件和選取參數下的ABH最優幾何參數組合如表5所示。

表5 本文所選試驗指標的最優組合

單聲學黑洞能在較寬的高頻頻帶內實現振動能量的匯聚，但是將聲學黑洞應用到實際結構，如汽車的車身板件中時，經常需要對低頻的振動和噪聲進行抑制，這就需要較大的聲學黑洞外半徑，然而這不利于其布置和加工。此外，車用板件形狀多樣，內嵌單個聲學黑洞的應用范圍有限。而內嵌于板結構中的多個聲學黑洞組成的陣列結構具有實現有效操控頻帶的改善和操控效果的特性，因此研究聲學黑洞陣列的能量匯集具有重要意義。

2 聲學黑洞陣列頻率特性分析

2.1 二維聲學黑洞陣列模型的建立

將多個二維聲學黑洞排布于板結構內，即得到內嵌于板結構的二維聲學黑洞陣列。相比于單個二維聲學黑洞，二維聲學黑洞陣列的存在不僅可以進一步減輕板結構質量，還能改變結構的頻率特性，從而影響板結構的振動能量匯集。本文針對兩聲學黑洞組成的簡單聲學黑洞陣列，分析3 種不同陣列形式，并分別與同尺寸的內嵌單個二維聲學黑洞板結構進行頻譜特性對比，研究聲學黑洞陣列結構上對能量匯集效應的影響。

首先根據正交試驗所得最優組合，構建內嵌單個二維聲學黑洞板結構，如圖6(a)所示。在此基礎上引入相同大小和構型的另一個聲學黑洞結構，進而得到具有相同最優構型的1×2聲學黑洞陣列的板結構，如圖6(b)所示，其中兩個聲學黑洞中心的距離為200 mm。改變兩個聲學黑洞結構的位置，可得到2×1聲學黑洞陣列板結構，如圖6(c)所示。其中兩個聲學黑洞呈對稱分布，它們中心的距離為200 mm，中心距右邊界距離為200 mm。進一步改變聲學黑洞的位置，令兩個黑洞中心的水平距離和豎直距離都為200 mm，并且兩者關于板中心呈中心對稱，得到中心連線與水平線呈45 度的聲學黑洞陣列板結構，如圖6(d)所示。

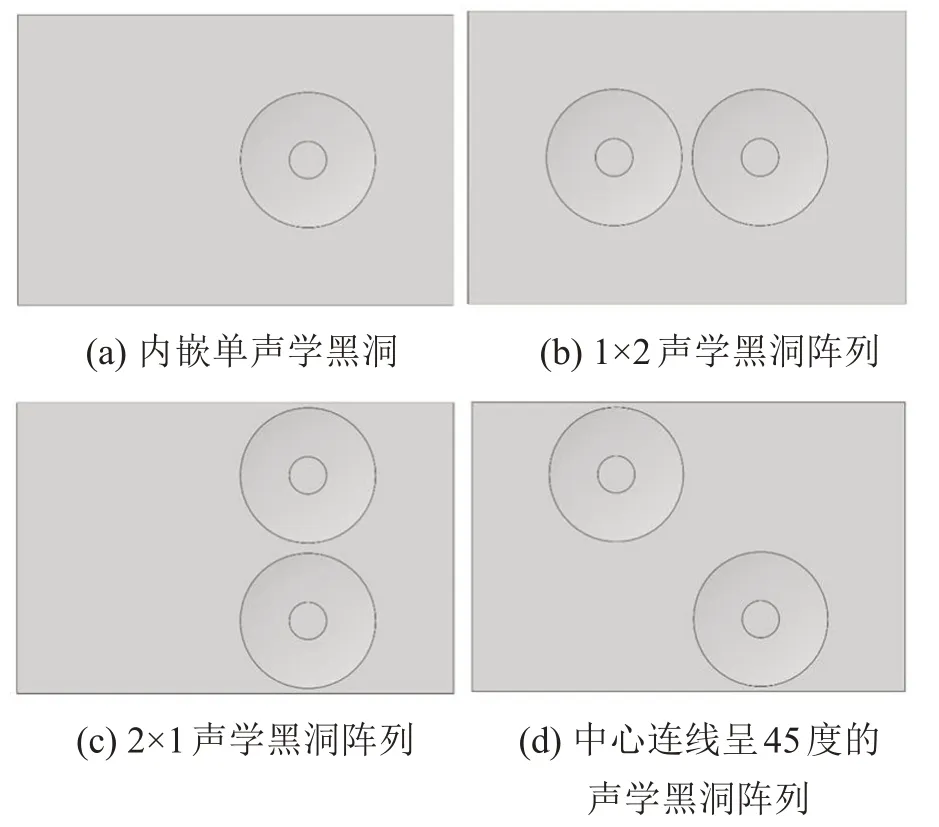
圖6 單聲學黑洞和不同形式的陣列結構

2.2 能量匯集效應的頻率特性分析

分別將圖6中的4 個幾何模型導入Hypermesh及ABAQUS 軟件中建立有限元模型，如圖7所示。其中激勵位置及大小與邊界條件與1.2 節中完全一致，激勵頻率范圍為200 Hz～1 800 Hz，間隔2 Hz。

圖7 激勵點位置和約束示意圖

為了表征陣列的能量匯聚效果，分別計算陣列中兩個聲學黑洞單元的中心平臺內所有節點的垂直于板面方向的空間均方速度，并將二者求和，以此作為評價聲學黑洞陣列結構能量匯集效應強弱的指標：

式中：v1n為單元1 中心均勻厚度平臺某點的法向速度，v*1n是其法向速度的共軛；S1是單元1中心平臺的面積；v2n為單元2 中心均勻厚度平臺某點的法向速度，v*2n是其法向速度的共軛；S2是單元2中心平臺的面積。顯然，該值越大表明聲學黑洞陣列能量匯集效應越強。

對圖7中所示的4 個模型的有限元計算結果進行處理，分別得到它們在200 Hz～1 800 Hz 頻率范圍內的空間均方速度，從而得到聲學黑洞結構振動響應在200 Hz～1 800 Hz 范圍隨頻率變化的曲線。為方便比較，將3 種陣列結構的空間均方速度圖分別與單聲學黑洞結構進行比較，結果如圖8至圖10所示。

圖8 1×2陣列板與單聲學黑洞板空間均方速度對比

圖9 2×1陣列板與單聲學黑洞板空間均方速度對比

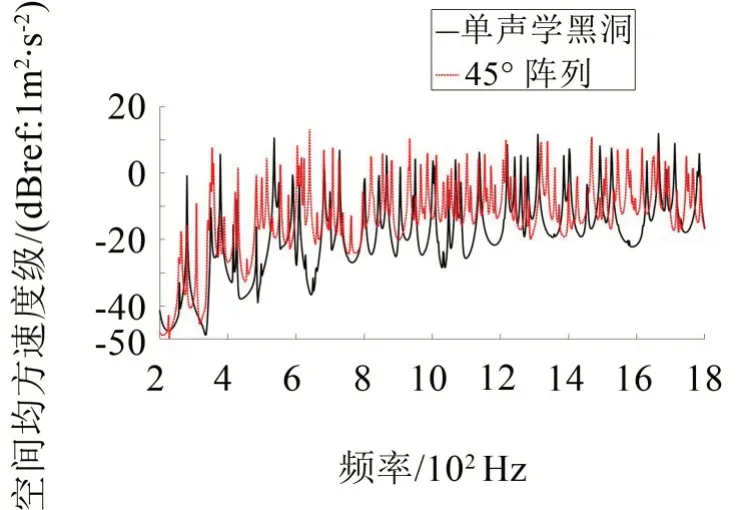
圖10 45°陣列板與單聲學黑洞板空間均方速度對比

從上述曲線可以看出，在200 Hz～300 Hz 范圍內，4 種板結構明顯的共振峰均只有一個，且1×2 聲學黑洞陣列板的共振峰最高，高于單聲學黑洞板共振峰達3 dB左右，而2×1聲學黑洞陣列板和45°排布的陣列板共振峰較低，分別低于單聲學黑洞板共振峰8 dB和18 dB左右。這表明在200 Hz～300 Hz的低頻范圍內，橫向排布的1×2 陣列結構通過單元的合理排布改變了低頻下的板結構振動特性，實現了更優的能量匯聚；而2×1聲學黑洞陣列板和45°陣列板的黑洞單元排布方式削弱了低頻下的能量匯聚效果。這表明通過調整陣列結構的單元排列方式能夠增強或抑制低頻范圍內的振動響應。

在400 Hz～1 800 Hz的頻率范圍內，3種陣列結構的空間均方速度曲線相比于單聲學黑洞板對應曲線整體上有一定的提高，其中500 Hz以上頻帶內這種提升較為明顯。如圖8所示，500 Hz 以上頻帶內橫向排布1×2聲學黑洞陣列板的共振峰值相對于單聲學黑洞板而言，大部分均有10 dB以內的提升，而極少部分頻率對應的單聲學黑洞板峰值較高。圖9所示的縱向排布2×1聲學黑洞陣列板的共振峰值在800 Hz～1 200 Hz 頻段內相比于單聲學黑洞較高，其他頻率范圍內共振峰峰值與單黑洞板相當。而圖10 所示的45°排布的陣列結構的共振峰峰值在700 Hz以上的頻率范圍內均與單黑洞板相當，但其共振峰數量明顯多于單聲學黑洞，也能在研究頻率范圍內增強能量匯聚水平。

為比較三種陣列結構在該頻段內的能量匯聚效果，分別計算它們在200 Hz～1 800 Hz 頻段內的空間均方速度的平均值，結果如表6所示。將單個聲學黑洞的計算結果與表3中正交試驗所得結果對比可以看出，該幾何參數對應的聲學黑洞結構的能量匯集效果最好，進而驗證了正交試驗所得最優構型的有效性。此外，可以看出三種陣列結構的能量匯集效果均優于單聲學黑洞結構，表明了聲學黑洞陣列結構的優越性。對于不同排布方式的陣列結構的能量匯聚效果，以1×2 橫向排布的陣列最優，45°排布陣列次之，2×1縱向排布的陣列最差，這表明對于本文研究的板結構，橫向依次排布的陣列結構能量匯聚效果最好，單元排布方式越趨向于縱向排布，能量匯聚效果越差。

表6 3種陣列空間均方速度在200 Hz～1 800 Hz頻段內的平均值/10-2( m2 ?s-2)

上述結果表明，在一定頻帶范圍內，兩個聲學黑洞組成的陣列的能量匯聚效果比單聲學黑洞更為明顯。這種現象出現的原因如下，一方面在內嵌兩個聲學黑洞的板結構中，厚度較薄部分的面積增加，板結構整體的剛度下降，在施加激振力不變的情況下，結構的振動響應增強，某些頻率下的空間均方速度峰值增大；另一方面，兩個聲學黑洞組成陣列后，利用不同的排布方式，增加了原有結構的復雜程度，提高了聲學黑洞結構與原有板結構的頻率匹配機會[15]，豐富了板結構的模態特性，導致其空間均方速度峰出現次數增加，能量匯聚效果得以提升；此外，聲學黑洞數量增加使能量匯聚區域面積增大，更多的振動能量被匯聚在聲學黑洞中心平臺區域。

上述研究還表明橫向排列的聲學黑洞陣列結構具有更好的能量匯聚效果。可能的原因是，在本文所考慮的激勵形式和約束方式下，板結構中振動能量以橫向傳播為主導形式，而橫向排布的陣列結構使橫向傳播的振動能量更加充分地經過聲學黑洞區域，得到更強的能量匯聚效果；而振動能量向著縱向排布的聲學黑洞陣列結構傳播時，需要先分散傳播或通過邊界反射后進入黑洞區域，再在其中發生匯聚，振動能量匯聚不如前者充分。

綜上可知，對于本文中所考慮的板結構模型，內嵌于板結構中的聲學黑洞陣列可在200 Hz～1 800 Hz的頻帶內增強板結構內的能量匯集效應，使更多的能量匯聚于聲學黑洞內。進而在中心平臺粘貼阻尼材料就能夠實現較高的能量耗散效率。同時，陣列中各單元的排布方式對能量匯聚效應有較大影響，在利用聲學黑洞陣列結構吸收振動能量時，應合理設計陣列單元的排布方式，以進一步增強能量匯集效應。

3 結語

本文利用有限元法，首先通過正交試驗對內嵌于板結構內的單二維聲學黑洞進行參數分析與優化設計，得到了特定板結構尺寸下最優的聲學黑洞構型參數。基于這組幾何參數，設計了內嵌于板結構的不同聲學黑洞陣列，分別對這幾種陣列結構進行能量匯聚效果研究，得到陣列結構以及排布方式對于能量匯聚特性的影響，從而提升陣列結構在實際應用中粘貼阻尼材料后的減振降噪效果。研究結論如下：

(1)板結構的能量匯集效應隨著殘余厚度、冪指數和聲學黑洞外半徑改變而改變，且對于給定的板件結構存在最優的聲學黑洞構型參數；

(2)相對于內嵌于板中的單聲學黑洞結構，聲學黑洞陣列能夠提升聲學黑洞的板結構匯集能量的效果。對于本文所研究的板結構而言，在激勵頻率200 Hz～1 800 Hz 范圍內，聲學黑洞陣列結構的振動能量匯集能力明顯強于單聲學黑洞結構；

(3)內嵌于板結構中的聲學黑洞陣列的排布方式對于整個聲學黑洞陣列板結構的能量匯聚效應有很大影響。對本文中研究的激勵位置和邊界條件而言，考慮的三種排列形式中1×2 橫向排布的陣列結構能量匯聚效果最優，45°排布陣列結構次之，2×1排布陣列結構最差，但陣列結構的能量匯聚能力均優于單聲學黑洞。為了更好地實現能量的匯聚，在板結構實際應用中應該優先考慮橫向排布的聲學黑洞陣列結構。

綜上所述，陣列結構可實現比單聲學黑洞結構更佳的能量匯聚效果，通過在高能量密度區域粘貼阻尼材料，可實現較高的能量耗散效率。本文對于聲學黑洞在汽車板件中的應用和聲學黑洞陣列的設計提供了參考，后續將對本研究進行實驗驗證，并進一步研究多聲學黑洞（多于2個）陣列結構的振動能量匯聚特性。