法向振動對Burridge-Knopoff模型Stick-Slip運動影響數值研究

姜 磊

（1.核工業理化工程研究院，天津 300180； 2.粒子輸運與富集國防重點實驗室，天津 300180）

Stick-Slip運動是含摩擦的動力學系統具有的典型特征之一，如琴弦撥動、輪軌接觸、剎車盤異響以及地震斷層等過程中均伴隨著Stick-Slip 現象[1–2]。Stick-Slip 造成動力學系統的非光滑特性，并產生負面效果，例如噪聲、能量損失、磨損以及部件失效等[3]，因而被廣泛研究。

上世紀60年代，Burridge和Knopoff在對地震進行研究時提出了Burridge-Knopoff模型，該模型已被推廣到其他動力學系統，并成為含摩擦動力學系統Stick-Slip 運動研究的主要模型[4]。實際工程領域中，該模型中滑塊所模擬的具體結構，如剎車片、機車輪等的振動形式通常較為復雜[5–7]。這些復雜的運動從機理上都可以采用Burridge-Knopoff 模型或在此模型上的改進模型來分析。近些年來，研究人員開展了大量研究。Emrullah[8]研究了Burridge-Knopoff模型求解的新方法；Kawamura等[9]模擬了該模型的快速斷裂現象，發現一維和二維模型存在顯著不同的斷裂行為；Amireghbali 等[10]采用該模型研究了彈性體和剛性表面的接觸動力學行為，比較了不同摩擦力模式下該模型的觸發動力學差異；Ueda等[11]，Kostic等[12]也采用該模型對地震現象中的動力學行為進行了研究。

在實際的工程領域中，Burridge-Knopoff模型的實際運動行為是較為復雜的，例如剎車盤異響時，卡鉗和剎車盤之間的相對運動不僅包含切向運動，還包含法向振動成分。目前，法向振動對Burridge-Knopoff 模型動力學行為的影響還沒有得到系統性研究。在文獻[7]中考慮了傳送帶的法向振動對模型運動行為的影響，研究結果表明，法向振動將導致滑塊與傳送帶之間的接觸力波動，進而影響到二者之間的摩擦力數值，并最終使得模型的運動行為趨向復雜。本研究重點考慮滑塊的法向振動對模型運動行為的影響，采用速度依賴型Stribeck摩擦模型研究考慮法向振動情況下Burridge-Knopoff 模型的Stick-Slip運動規律及各參數影響機制。

1 Burridge-Knopoff 模型考慮滑塊法向振動的運動模型建立

1.1 單滑塊Burridge-Konpoff模型

含單滑塊Burridege-Knopoff 模型如圖1所示，為了考慮滑塊在切向和法向兩個方向上的運動，建立x-y坐標系，其中x代表傳送帶切向，y代表傳送帶法向。

圖1 單滑塊Burridege-Konpoff模型

滑塊在法方向上存在幅值為A的微幅振動，振動角頻率為ω，相位為φ。滑塊在法向受恒定正壓力FN0作用，在切向則受到彈簧回復力及傳送帶摩擦力。為了簡化計算模型，假設滑塊法向振動行為具有獨立性，其振動幅值和頻率等保持恒定，同時不考慮傳送帶的法向振動行為。滑塊法方向振動位移y滿足（1）式：

根據D’Alembert原理，得到滑塊切向運動位移x滿足（2）式：

這里：Ff為滑塊與傳送帶間摩擦力數值，N；sgn 為符號函數，k為彈簧剛度系數，N/m。

1.2 摩擦模型

摩擦現象的精確數學建模是機械工程和控制領域研究的重要內容。目前，已有多種摩擦模型，包括庫侖模型，Dahl 模型，LuGre 模型，Stribeck 模型等。其中，Stribeck模型考慮到摩擦力對于相對速度的依賴性，隨速度先減小后增大變化趨勢，如圖2所示。

圖2 Stribeck摩擦模型圖像

Stribeck模型有各種表達形式，其中應用最為普遍的是指數衰減型[5]，表達式如下：

其中：vre為相對運動速度，Fex為切向外力，本例中為彈簧回復力，μs為靜摩擦系數，μc為庫侖動摩擦系數，Vs為Stribeck速度，δVs是用來控制Stribeck曲線形狀的速度參數，參考Armstrong[6]的研究結果將δVs取為2，從而得到高斯模型，η為黏性摩擦系數，FN為滑塊與傳送帶間的接觸正壓力，由于滑塊存在法向運動，FN滿足（4）式：

將式（1）式代入式（4），得到正壓力FN的表達式：

1.3 參數設置

本研究算例中Burridege-Knopoff模型的計算參數如表1所示。

表1 計算參數列表

2 不考慮法向振動情況下Stick-Slip運動響應分析

采用1.3 節中的參數設置，計算了模型運動響應。滑塊x方向的運動位移隨時間變化規律如圖3所示，對應的運動相平面如圖4所示。

圖3 滑塊x方向振動時域曲線

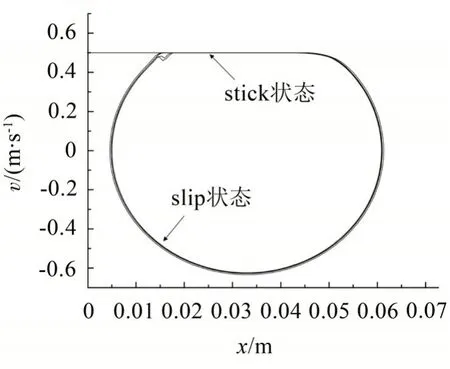
圖4 滑塊x方向Stick-Slip運動相平面

在上述相平面圖中可以看出，滑塊運動呈現典型的Stick-Slip 模式。在Stick 模式下滑塊與傳送帶之間無相對位移，二者之間的摩擦力表現為靜摩擦力；在Slip模式下滑塊與傳送帶之間產生相對運動，兩者之間的摩擦力表現為動摩擦力。

圖5為運動過程中滑塊與傳送帶之間摩擦力隨時間變化曲線。從曲線中可以看出不同運動狀態下摩擦力的數值大小波動規律，同時可以明顯地觀察到摩擦過沖現象（Friction Overload）[6]，這種現象是Stick-Slip運動的典型特點。

圖5 滑塊-傳送帶接觸摩擦力時域變化曲線

3 考慮法向振動情況下Stick-Slip 運動響應分析

3.1 頻率影響規律分析

考慮滑塊法向振動后，模型運動模式發生變化。圖6給出了不同法向振動頻率情況下運動相平面圖，在該圖計算過程中，除了振動頻率，其他參數沿用表1中的參數設置。

圖6 不同法向振動頻率下的滑塊Stick-Slip運動

從圖6可以看出，隨著法向振動頻率增加，滑塊運動規律趨向于復雜，運動周期性逐漸被破壞，運動相平面呈現不規則特點。為了進一步分析振動頻率的影響規律，圖7給出了滑塊運動幅值隨頻率變化規律。該圖表明：隨著頻率增加，滑塊運動幅值發生顯著變化。當頻率在80 Hz 以內時，運動幅值隨著頻率增加而增加；當頻率超過80 Hz之后，隨振動頻率增加運動幅值呈現先減小后增大的趨勢，當頻率在80 Hz～200 Hz 之間時，系統呈現出混沌現象，當頻率大于200 Hz時，系統呈現動力學分岔現象。

圖7 滑塊x向運動幅值隨法向振動頻率變化規律

3.2 相位影響規律分析

圖7給出了不同法向振動相位情況下運動相平面圖，在該圖計算過程中，除了振動相位外，其他參數沿用表1的參數設置。

從圖8可以看出，隨著法向振動相位變化，滑塊運動響應逐漸發生變化。圖9給出了滑塊運動位移受法向振動相位影響規律。可以看出，滑塊切向運動受到法向振動相位影響總體呈現周期性特點。與上文頻率影響情況類似，這里同樣存在混沌和分岔現象。在單個周期T=180°內，隨著相位增加，滑塊切向運動幅值呈現先增加后減小的總體變化趨勢。當相位角在0～60°和180°～240°之間變化時，系統呈現混沌現象；當相位角在60°～180°和240°～360°之間變化時，系統呈現動力學分岔現象。

圖8 不同法向振動相位下滑塊Stick-Slip運動

圖9 滑塊x向運動幅值隨法向振動相位變化規律

4 結語

本研究結果表明，Burridege-Knopoff 模型表現出Stick-Slip運動規律，滑塊與傳送帶之間存在無相對運動的粘著運動和相對滑動兩種典型運動狀態，在兩種狀態轉換過程中存在摩擦過沖現象。滑塊法向振動對模型的運動模式有顯著的影響，法向振動的頻率和相位的變化均會改變系統的運動行為。

考慮法向振動的單滑塊Burridege-Knopoff模型運動存在混沌或分岔現象，本研究模型具體表現為：

（1）當頻率超過80 Hz 時，隨著頻率增加，滑塊運動逐漸由混沌模式向分岔模式過渡。隨著相位增加，模型運動模式呈現周期性變化規律，周期為180°，并伴隨混沌與分岔現象；

（2）當相位角在0～60°和180°～240°之間時，系統呈現混沌現象；當相位角在60°～180°和240°～360°之間變化時，系統呈現分岔現象。