基于奇異譜分解和兩層支持向量機軸承故障診斷方法

湯天寶，周志健，張 濤，李 可，盧立新

(1.江南大學 機械工程學院，江蘇 無錫214122；2.江南大學 江蘇省食品先進制造裝備技術(shù)重點實驗室，江蘇 無錫214122)

在實際生產(chǎn)過程中，實時監(jiān)測機械設(shè)備的運行狀態(tài)具有巨大的經(jīng)濟價值。機械設(shè)備發(fā)生故障，輕則停機檢修，重則導致工作人員人身傷害。滾動軸承作為機械傳動部件的重要支撐零件，其狀態(tài)的監(jiān)測尤其重要。滾動軸承一旦出現(xiàn)故障將造成設(shè)備停止工作，往往會帶來無法估量的經(jīng)濟損失。因此，對滾動軸承的診斷研究具有重大的經(jīng)濟價值。由于工業(yè)生產(chǎn)環(huán)境復雜，背景噪聲干擾強，早期故障特征不明顯，提取效果較差，特征提取也就難以實現(xiàn)。因此，如何消除背景噪聲干擾，提取故障特征，顯得至關(guān)重要。

目前，傳統(tǒng)的滾動軸承故障診斷方法以快速傅里葉變換(Fast fourier transform，F(xiàn)FT)為主。短時傅里葉對FFT 進行了改進，雖然在一定程度上解決了FFT 處理非線性信號的局限性，但是在突變信號處易發(fā)生信號丟失現(xiàn)象。小波變換是信號進行時頻處理的工具，在時頻聚集方面具有良好的表現(xiàn)，但是在時間和頻率之間無法完成自適應(yīng)。為了完成自適應(yīng)，李心一等[1]在FFT 的基礎(chǔ)上，提出了一種將改進的能量算子和自適應(yīng)濾波算法相結(jié)合的方法，實驗結(jié)果顯示在少量訓練樣本情況下該方法具有較高的診斷精度。丁顯等[2]將自適應(yīng)的小波變換技術(shù)應(yīng)用到旋轉(zhuǎn)機械故障診斷領(lǐng)域，通過風電試驗臺故障案例驗證了所提方法的可行性。Bonizzi等[3]提出了一種改進的SSD方法，采用自適應(yīng)法則選取矩陣維數(shù)，該方法將強背景噪聲下的原始信號依次分解為若干個頻率不同的SSC 和殘差，每個SSC 表示原信號的局部特征。

隨著人工智能的蓬勃發(fā)展，將智能算法應(yīng)用于故障診斷領(lǐng)域的思路受到廣泛關(guān)注[4]。許多研究者把傳統(tǒng)故障診斷方法與智能算法相結(jié)合，提出了一系列智能軸承故障診斷算法。俞昆等[5]基于多傳感器信息融合提出了一種軸承故障診斷方法，識別率較高。宮文峰等[6]對卷積神經(jīng)網(wǎng)絡(luò)改進，并通過結(jié)合支持向量機(Support vector machine，SVM)構(gòu)建分類算法完成故障分類，應(yīng)用于電機軸承的快速智能診斷，算法識別率高，效果明顯。李華等[7]提出了將優(yōu)化頻帶熵和集合經(jīng)驗模態(tài)分解相結(jié)合的診斷方法，在仿真實驗和實際軸承故障實驗中都取得了較好的診斷結(jié)果。

軸承故障數(shù)據(jù)具有樣本較少，一般樣本集僅僅在100至500左右，維數(shù)較高的特點。SVM在高維、小樣本數(shù)據(jù)分類中表現(xiàn)良好，因此在軸承故障診斷中得到了廣泛應(yīng)用。趙樹延等[8]提出了一種基于偏最小二乘法和支持向量機的故障診斷方法，實驗結(jié)果顯示，該方法具有較高的準確率。姜久亮等[9]基于延拓局部均值分解和SVM 提出了一種智能故障診斷方法，實驗表明該方法能較好進行故障分類。然而由于環(huán)境噪聲等影響造成傳統(tǒng)SVM 對噪聲較為敏感，有時難以表征信號與設(shè)備運行狀況間的復雜映射關(guān)系，導致診斷精度不理想[10]。因此，一種兩層支持向量機的模式識別方法被提出[11]，該方法通過建立兩層結(jié)構(gòu)學習模型，挖掘出數(shù)據(jù)的深層特征，以此提高分類準確率。

基于以上分析，一種基于奇異譜分解和兩層支持向量機的軸承故障診斷方法被提出。首先采集信號構(gòu)建信號矩陣，然后對矩陣進行奇異譜分解，得到奇異譜分量。依據(jù)自適應(yīng)峭度準則重構(gòu)信號矩陣，進行特征提取，得到特征向量矩陣作為輸入。通過輸入層對信號訓練，從而獲得淺層信號故障特征，進行降維處理生成新的特征向量矩陣，最后在輸出層完成分類。通過在實驗室風機實驗臺上進行驗證，結(jié)果表明該方法具有良好的診斷性能。

1 奇異譜分解及提取特征向量

1.1 奇異譜分解

作為一種自適應(yīng)信號處理方法，SSD 能將強背景噪聲下的信號依次分解為若干個頻率不同的SSC和殘差分量[12]。具體計算過程如下：

(1)構(gòu)建信號矩陣。對于信號數(shù)據(jù)y(n)，選取數(shù)據(jù)長度N和矩陣維數(shù)M，重構(gòu)為M行N列的矩陣Y，矩陣Y的第i行為：

其中：i=1,2,???M，即矩陣：

(2)確定矩陣維數(shù)M。首先，計算第j次迭代殘差分量Vj(n)的功率譜密度（Power spectral density，PSD），殘差分量Vj(n)公式為|：

其中：V0(n)=y(n),j≥2。

通過找到PSD 峰值最大值，估計最大值處對應(yīng)的頻率fmax。在首次迭代中，如果歸一化頻率fmax/Fs≤10-3，殘差將作為重大分量，將M設(shè)置為N3。當j>1，矩陣維數(shù)M=1.2×(fmax/Fs)。

其次，重構(gòu)分量信號j。在首次迭代完成后，如果產(chǎn)生一個重大分量，在滿足Y1=σ1μ1VT1時，只選取第1 個左、右特征向量來獲取g1(n)。否則，當j>1，必須獲得一個分量序列g(shù)1(n)作為時間尺度。在頻譜[fmax-Δf,fmax+Δf]范圍內(nèi)，對主峰能量影響最大的特征組，創(chuàng)建子集Ij(Ij={i1,???,ip})。通過對角平均重構(gòu)矩陣YIj=Yi1+???+Yip分量。

使用3 個高斯函數(shù)之和來模擬該輪廓，以便估計主峰帶寬Δf。每個高斯函數(shù)代表一個譜峰，表達式為：

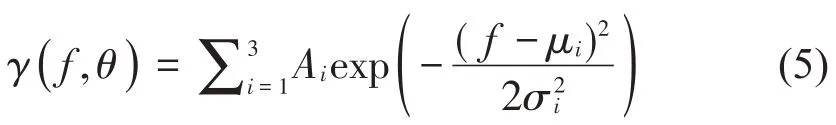
式中：Ai為第i個高斯函數(shù)的幅值；μi表示位置點；σi為帶寬；θ=[Aσ]T為參數(shù)矢量，滿足A=[A1,A2,A3]和σ=[σ1,σ2,σ3]。

第一個函數(shù)代表主譜峰，對應(yīng)頻率fmax。第二個函數(shù)代表次譜峰，對應(yīng)頻率f2。第三個函數(shù)記錄前2個譜峰之間任意峰值的頻率。依據(jù)此模型得：

為了獲得模型參數(shù)Ai，首先給定擬合的初始值，再對模型進行加權(quán)最小二乘擬合，即：

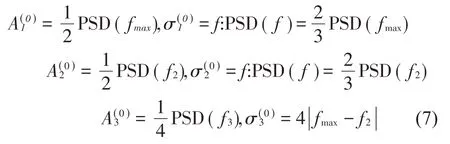
參數(shù)Ai最優(yōu)值根據(jù)萊文貝格-馬夸特算法確定。主峰帶寬Δf=2.5σ1，σi為設(shè)定的初始值。為了重構(gòu)第j個信號分量，進行第2 次迭代，設(shè)置尺度因子調(diào)節(jié)殘差信號Vj(n)與g(j)(n)的差值，即：

(3)迭代終止條件。將估算出的分量g(j)(n)從原信號中提取出來，以此獲得殘差分量V(j+1)(n)=V(j+1)(n)-(n)，計算殘差分量和原始數(shù)據(jù)的歸一化均方差（Normalized Mean Squared Error，NMSE），即：

設(shè)定NMSE的下限閾值0.5%，當計算結(jié)果小于下限閾值，終止迭代；否則，將殘差分量視作輸入信號重復上述迭代過程，即：

式中：m為獲得的分量序列個數(shù)。

1.2 信號重構(gòu)

經(jīng)過SSD 分解后，信號轉(zhuǎn)換為若干個不同頻率的SSC和殘差分量。但如何選取包含有效信息的奇異譜分量成為難點。因此，本文提出一種基于峭度自適應(yīng)準則的SSD 方法[13]，該方法能夠自適應(yīng)選取SSC進行信號重構(gòu)。

峭度數(shù)學表達式為：

式中：μ為信號y的均值；σ為信號y的標準差。

通常認為滾動軸承正常運轉(zhuǎn)情況下的信號峭度應(yīng)小于3，而當發(fā)生故障時，SSD 分解后的各SSC 分量對應(yīng)的峭度會增大。為了解決各分量之間峭度差異大的問題，提出一種改進峭度準則[14]。當時，所有滿足條件的分量都將被重構(gòu)；當時，依據(jù)峭度大小選取前80%的分量進行重構(gòu)；當時，所有分量全部用于重構(gòu)，此處可以近似認為信號正常，軸承正常運轉(zhuǎn)。

1.3 提取特征向量

對早期故障沖擊脈沖較為敏感的參數(shù)為峭度、峰值、裕度指標和脈沖指標，其穩(wěn)定性較差；偏斜度和波形因子穩(wěn)定性好，但對早期故障不敏感。因此綜合考慮，提取重構(gòu)信號的波形因子S、峰值C、脈沖因子I、裕度因子CL、偏斜度Cw和峭度Kr，構(gòu)建特征向量U=(S,C,I,CL,Cw,Kr)。

2 兩層結(jié)構(gòu)支持向量機

2.1 支持向量機

對于由N組數(shù)據(jù)組成的訓練樣本集D=，其中，xi∈RM是第i個訓練樣本，yi={-1,1}為樣本標簽。

SVM 的優(yōu)化目標是對超平面wTx+b=0 的分類，如圖1所示。

圖1 SVM最優(yōu)分類線

通過拉格朗日對偶性原則，將分類問題變換為求解拉格朗日因子α的優(yōu)化問題[15]。考慮對誤差的寬容程度，引入懲罰因子C。針對數(shù)據(jù)線性不可分的情況，選擇合適的核函數(shù)κ(?,?) 實現(xiàn)樣本高維特征空間的線性可分，目標函數(shù)為：

由最小最優(yōu)化原則[16]得到優(yōu)化目標α，將其帶入分類函數(shù)中求解，分類函數(shù)為：

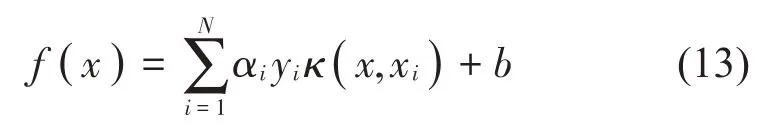
2.2 兩層支持向量機

TSVM在訓練過程中獲得高級特征抽象。在此結(jié)構(gòu)中輸入和輸出層均為一個標準SVM，且僅有輸入層和輸出層。訓練樣本經(jīng)輸入層訓練后，搭建與輸出層之間的映射關(guān)系，經(jīng)過輸出層完成分類。

通過對訓練樣本X={(xi,yi)}Ni=1進行降維處理[15]，將其放入輸入層訓練，得到一組向量(α1,α2,α3,???,αN)和數(shù)量為Q的支持向量(β1,β2,???,βQ)，將對應(yīng)的拉格朗日因子(α1,α2,???,αQ)提取出來，進行信號特征提取，公式為：

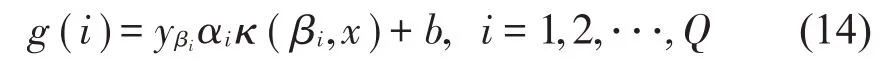
其中：βi為支持向量；αi為βi對應(yīng)的拉格朗日因子；yβi為標簽；b為偏置。對于訓練樣本xi∈RN,i=1,2,???,xi經(jīng)過特征提取得到新的樣本x2i：

則原始數(shù)據(jù)xi∈RN變?yōu)閤i∈RQ，將得到的新的訓練樣本作為輸出層的輸入樣本。

對于測試樣本，按照特征公式映射，判別函數(shù)為：

其中：βi為第i個支持向量；ο()表示測試樣本映射后的特征為輸出層的偏置。

2.3 SSD-TSVM故障診斷流程

故障診斷SSD-TSVM算法流程如圖2所示。對滾動軸承振動信號進行SSD處理后得到的不同頻率的信號分量，采用改進的峭度準則進行信號重構(gòu)。計算重構(gòu)信號的多個時域特征指標生成特征矩陣。在第一層SVM 進行“降維處理”，生成新的特征矩陣，最后在第二層SVM完成各種故障類型軸承的分類，計算識別準確率。

圖2 SSD-TSVM故障診斷流程圖

3 西儲大學數(shù)據(jù)驗證

為驗證所提SSD-TSVM 方法的有效性，選用凱斯西儲大學驅(qū)動端軸承的數(shù)據(jù)進行測試、分析，數(shù)據(jù)包括正常、內(nèi)圈故障、外圈故障和滾動體故障狀態(tài)下實驗數(shù)據(jù)，軸承參數(shù)如表1所示[17]。其中采樣頻率Fs=12 000 Hz，故障直徑0.007″，電機空載，電機轉(zhuǎn)速1 797 r/min。

表1 軸承相關(guān)參數(shù)

數(shù)據(jù)驗證選取前10 s的數(shù)據(jù)進行分析。原始信號時域圖如圖3所示。每種故障狀態(tài)下均包含239個樣本，隨機選取70個作為訓練樣本，剩余169個作為測試樣本，得到總訓練樣本數(shù)280，總測試樣本數(shù)676，構(gòu)建TSVM的訓練數(shù)據(jù)集和測試數(shù)據(jù)集。

圖3 原始數(shù)據(jù)信號

計算對應(yīng)特征值，得到特征向量Ui=(Si,Ci,Ii,CL i,Cw i,Kri),i=1,2 ???,120。將訓練樣本輸入TSVM進行分類。實驗中TSVM的核函數(shù)選擇高斯核函數(shù)，通過五折交叉驗證獲得核函數(shù)系數(shù)σ和懲罰因子C。其中第一層C=1.5,σ=10，第二層C=2,σ=2.5。分類測試結(jié)果正確率為98.08%。實驗結(jié)果表明該方法具有良好的準確率。

4 實驗驗證

為進一步測試SSD-TSVM 在實際應(yīng)用中的分類效果，用圖4所示實驗平臺采集風機軸承不同狀況下的振動信號，其中包括軸承正常、軸承滾動體故障、軸承外圈故障和軸承內(nèi)圈故障共4種狀態(tài)。

圖4 風機實驗平臺

選用PCBMA352A60型號加速度傳感器采集振動振動信號，傳感器的靈敏度為10 mV/g。軸承如箭頭所指。通過人工線切割方法分別在軸承內(nèi)圈、外圈和滾動體上加工出微小傷痕模擬軸承故障狀態(tài)，軸承故障的傷痕大小為0.25 mm×0.7 mm（寬×深）。軸承加工故障實物以及軸承參數(shù)如圖5和表2所示。電機轉(zhuǎn)速分別為1 000 r/min和800 r/min時的2組數(shù)據(jù)，采樣頻率設(shè)定為50 kHz，采樣時間為20 s。選取每種狀態(tài)下信號前10 s 采集的數(shù)據(jù)點作為樣本，即樣本數(shù)據(jù)為500 000。每種故障類型包含100個樣本，每個樣本5 000 數(shù)據(jù)點。設(shè)置隨機選取70個樣本作為訓練樣本，剩余30 個樣本作為測試樣本，得到訓練樣本總數(shù)280，測試樣本總數(shù)120，構(gòu)建TSVM的訓練數(shù)據(jù)集和測試數(shù)據(jù)集。

表2 軸承相關(guān)參數(shù)

圖5 故障軸承

對于上述2 組數(shù)據(jù)，分別采用原始數(shù)據(jù)結(jié)合支持向量機(SVM)，原始數(shù)據(jù)結(jié)合兩層支持向量機(TSVM)，奇異譜分解結(jié)合支持向量機(SSVM)，經(jīng)驗模態(tài)分解結(jié)合支持向量機(ESVM)，經(jīng)驗模態(tài)分解結(jié)合兩層支持向量機(ETSVM)。分類結(jié)果與SSD-TSVM方法進行對比。

實驗中SVM 和TSVM 均選擇高斯核函數(shù)作為核函數(shù)類型，通過五折交叉驗證獲得核函數(shù)系數(shù)σ和懲罰因子C。分別對轉(zhuǎn)速在800 r/min 和1 000 r/min工況下的軸承振動數(shù)據(jù)進行分類。

1 000 r/min數(shù)據(jù)1的各方法及其相應(yīng)的參數(shù)：

①SVM（原始數(shù)據(jù)）C=2，σ=1；

②TSVM（原始數(shù)據(jù)）第一層C=1，σ=1.5；第二層C=25，σ=0.3；

③SSVM中C=1，σ=0.6；

④ESVM中C=1.2，σ=0.2；

⑤ETSVM 第一層C=1.2，σ=0.2，第二層C=1.5，σ=1；

⑥SSD-TSVM 第一層C=3，σ=5，第二層C=5，σ=0.1。

800 r/min數(shù)據(jù)2的各方法及其相應(yīng)的參數(shù)：

①SVM（原始數(shù)據(jù)）C=2，σ=1；

②TSVM（原始數(shù)據(jù)）第一層C=2，σ=0.6，第二層C=4，σ=2；

③SSVM中C=1.5，σ=1；

④ESVM中C=1.4，σ=0.5；

⑤ETSVM 第一層C=2.5，σ=1.2，第二層C=1.5，σ=1；

⑥SSD-TSVM 第一層C=3，σ=5，第二層C=5，σ=0.1。

診斷結(jié)果如表3與圖6所示。

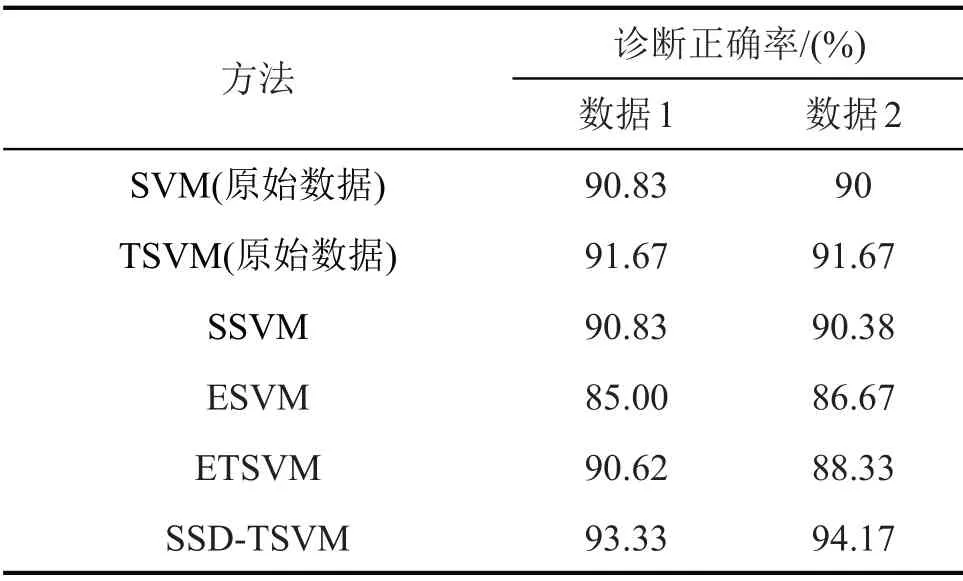
表3 診斷正確率

圖6 故障診斷正確率

從表2與圖6分析數(shù)據(jù)類型1可知，對于原始數(shù)據(jù)使用SVM 與TSVM 的診斷率分別為90.8 %與91.67%，使用TSVM 的診斷率高于SVM；對信號進行SSD與EMD后使用SVM進行分類的診斷正確率分別為90.83 與85%，采用SSD 進行故障診斷識別率明顯高于EMD 與SVM 結(jié)合的診斷識別率；SSDTSVM診斷正確率為93.33%，高于同等條件下對比的所有其余方法。同時，數(shù)據(jù)2分類準確率與數(shù)據(jù)1整體趨勢相同，SSD-TSVM 方法正確率為94.17%。因此，基于奇異譜分解與兩層支持向量機相結(jié)合的故障診斷方法SSD-TSVM具有較高的識別率，能夠有效地完成滾動軸承的故障診斷。

5 結(jié)語

為了解決強背景噪聲的干擾，數(shù)據(jù)量少等問題，一種基于奇異譜分解和兩層支持向量機的軸承故障診斷方法SSD-TSVM 被提出。分別對公開數(shù)據(jù)集和實驗室風機軸承數(shù)據(jù)1 和2 進行驗證。實驗結(jié)果表明，SSD-TSVM方法在小樣本，多分類情形下具有良好的分類結(jié)果，分類準確率分別為98.08 %、93.33%和94.17%。與其他同類型軸承故障診斷方法相對比，SSD-TSVM 方法在各種實驗中都具有較高的準確率。但是測試數(shù)據(jù)集僅在公開數(shù)據(jù)集和風機數(shù)據(jù)集上進行了驗證，其他多種軸承實驗數(shù)據(jù)仍需進一步驗證。