基于CFD和風洞試驗的鋼桁梁懸索橋顫振穩(wěn)定性分析

藍先林，周禮平，廖 斌，何 淼，徐向東，朱承前

(1.貴州省交通規(guī)劃勘察設計研究院股份有限公司，貴陽550081；2.中鐵武漢勘察設計研究院有限公司，武漢430074）

隨著“交通強國”等戰(zhàn)略的提出，我國西南地區(qū)橋梁建設得到迅猛發(fā)展。懸索橋是一種剛度小且主要由主纜受力的柔性體系橋梁，常用于山區(qū)峽谷溝壑地區(qū)。這類地區(qū)風環(huán)境復雜，風產生的顫振對懸索橋的破壞將是毀滅性的[1]。因此，十分有必要對復雜山區(qū)的懸索橋顫振穩(wěn)定性進行專題研究。

橋梁顫振問題是一種發(fā)散問題，橋梁結構是否發(fā)生顫振，主要與主梁斷面形式、懸索橋關鍵頻率和風環(huán)境有關[2]。國內外學者主要用風洞試驗[3]和CFD(Computational fluid dynamics)數值模擬[4]兩種方法對橋梁振動控制[5－7]進行研究。徐洪濤等[8]基于某千米級大跨度鋼桁梁懸索橋主梁節(jié)段模型試驗，得到了與橋梁顫振穩(wěn)定性有關的三分力系數和8個顫振導數，并從理論和經驗兩方面評價了該鋼桁梁懸索橋的顫振穩(wěn)定性能。董佳慧等[9]基于穩(wěn)定板、導流板、風嘴等氣動優(yōu)化措施，結合節(jié)段模型試驗，研究了某懸索橋的顫振穩(wěn)定性。熊龍等[10]先后利用CFD 數值模擬和風洞試驗，研究了某鋼桁梁懸索橋顫振性能和氣動優(yōu)化措施。Thai 等[11]、Wang 等[12]和Zhu 等[13]等研究了多塔懸索橋顫振性能，詹昊等[14]、Boberg 等[15]和Bakis 等[16]等基于流固耦合和氣動導數計算了懸索橋的顫振臨界風速。上述學者僅探究了平原和海峽地區(qū)懸索橋的顫振穩(wěn)定性問題，而對復雜山區(qū)的鋼桁梁懸索橋顫振問題研究較少。

基于上述研究，以山區(qū)某鋼桁梁懸索橋為研究背景，結合CFD 數值模擬和風洞試驗，從氣動導數和流固耦合兩方面探究復雜山區(qū)風環(huán)境作用下鋼桁梁懸索橋顫振穩(wěn)定性問題，可為同類橋梁抗風設計提供參考。

1 基本參數確定

1.1 工程背景

以貴州省某超大跨度鋼桁梁雙塔懸索橋為研究背景，探究復雜山區(qū)超大跨鋼桁梁懸索橋顫振穩(wěn)定性研究。該橋主跨為1 100 m，主纜邊跨分別為302 m、123 m。加勁梁采用板桁結合加勁梁，加勁梁標準斷面寬為B=27.0 m，桁架高為H=7.2 m。主纜采用抗拉強度為1 860 MPa 的高強度鍍鋅鋁合金鋼絲，共173股，每股由91根直徑為5.30 mm的鋼絲組成。橋塔采用混凝土橋塔，主塔塔高分別為135 m、139 m。

1.2 風參數的確定

根據設計資料可知，本橋距貴陽市大約60 km～80 km，參考貴陽市基本風速來確定本橋橋位基本風速。據文獻[17]可知，在平坦開闊條件下，貴陽市10 m高度、100年重現期、10分鐘平均時距年最大風速（即橋位基本風速）為：

本橋橋位處于峽谷地區(qū)，對應的地表類別為D類地表，風剖面指數α0=0.30。橋梁設計基本風速為：

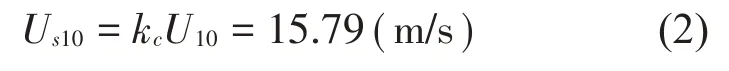
式中：kc表示基本風速地表類別轉換系數，對于D類地表取0.564。

橋面基準高度為：

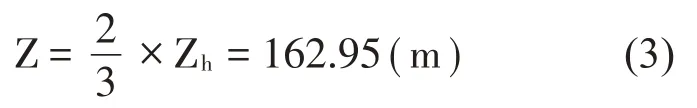
式中：Zh表示橋面距水面的高度。

加勁梁跨中基準高度為162.95 m，則對應加勁梁設計基準風速可按下式計算：

式中：kf為抗風風險系數，取為1.02。

成橋狀態(tài)-5°～+5°風攻角下橋梁顫振穩(wěn)定性按下式檢驗：

式中：Uf表示顫振臨界風速；Ud表示橋面高度設計基準風速；γf為顫振穩(wěn)定性分項系數，采用風洞試驗方法獲取顫振臨界風速時取1.15，采用CFD 方法獲取顫振臨界風速時取1.25；γt為風速脈動修正系數，該懸索橋橋主跨為1 100 m，橋位地表為D 類地表，故對應的風速脈動修正系數取γt=1.32；γα為攻角效應分項系數，當風攻角α為0°、±3°時取1.0，當風攻角α為±5°時，取0.7。

據式(5)可得到該橋風洞試驗和數值模擬的成橋態(tài)橋梁顫振檢驗風速如表1所示。

表1 成橋狀態(tài)橋梁顫振檢驗風速

1.3 動力特性參數

基于軟件ANSYS建立全橋有限元模型，并結合實際支座布置情況設置模型約束條件，其約束情況如表2所示。

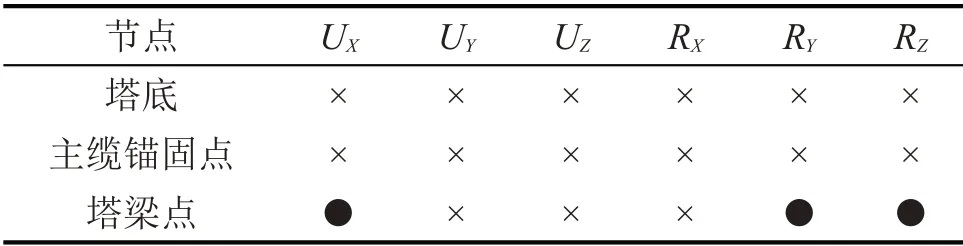
表2 約束情況

板桁結合加勁梁主桁桿件采用空間梁單元（BEAM189）模擬，橋面板采用空間殼單元（SHELL63）模擬，主纜、吊桿、中央扣均采用空間桿單 元（LINK10）模擬，橋塔采用空間梁單元（BEAM189）模擬，其有限元模型如圖1所示。

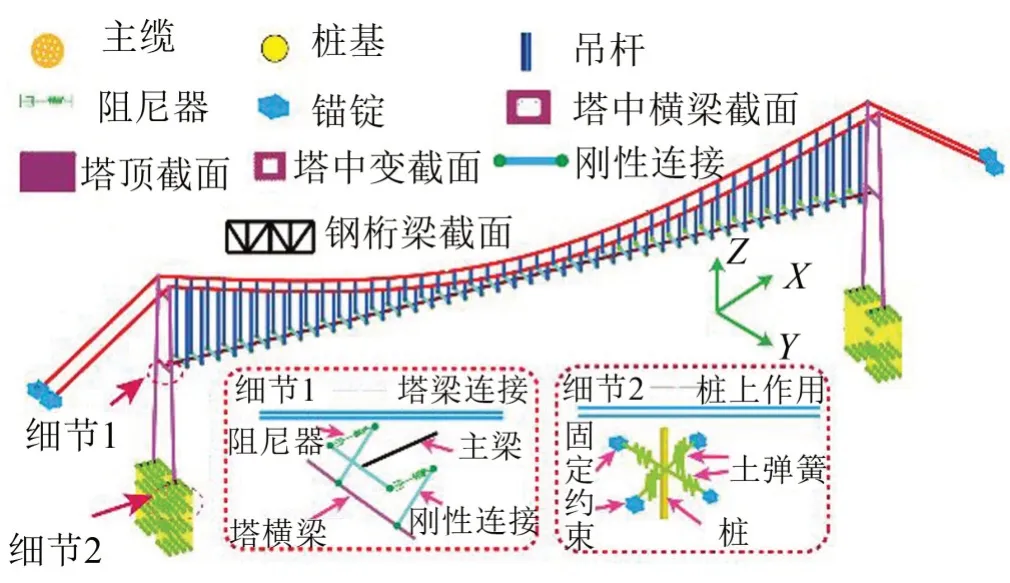
圖1 有限元模型

采用Block Lanczos 法計算結構動力特性，得到與抗風性能研究有關的關鍵頻率和振型如表3所示。

表3 關鍵頻率和振型

2 數值模擬

2.1 顫振臨界風速計算

根據CFD 識別的氣動導數對成橋狀態(tài)結構振型形狀相似的扭彎振型組合進行二維顫振臨界風速分析，得到顫振臨界結果，并將結果與流固耦合計算結果對比，進而確定顫振臨界風速。

(1)主梁斷面氣動導數計算

氣動導數是表征橋梁主梁斷面氣動自激力的重要氣動參數，其與結構斷面運動狀態(tài)線性組合表示氣動力的線性部分。根據Scanlan 自激力氣動力模型可知，主梁斷面氣動自激力表達式為：

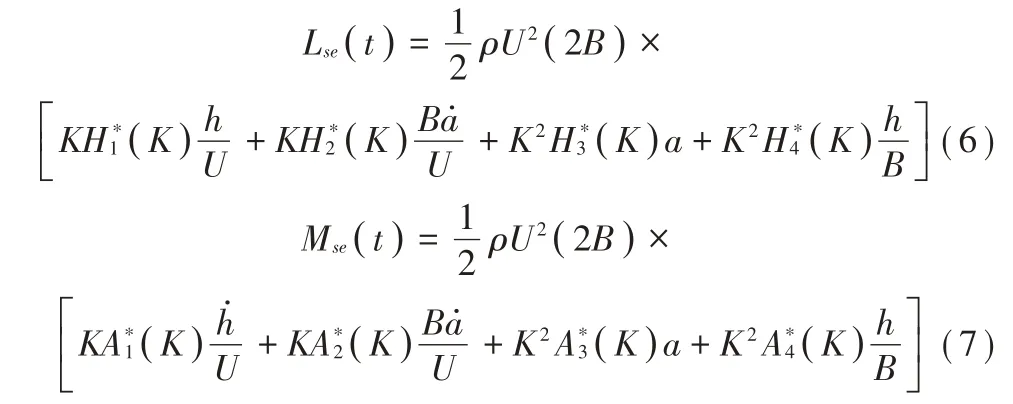
式中：ρ為空氣密度；K為折算頻率，K=2πfB/U；H*i、A*i為薄平板斷面的氣動導數，i為1～4；h和B分別為截面高度和寬度。

采用分狀態(tài)單自由度強迫振動的方式計算薄平板斷面在不同振幅的氣動自激力，其中風攻角α 分別為0°、±3°與±5°，風速U分別為2 m/s、4 m/s、6 m/s、8 m/s與10 m/s，扭轉運動振幅取為2.0°，豎向運動振幅分別取為3.0 cm，振動頻率f均為2.0 Hz。CFD計算模型仍采用靜三分力計算的網格，并設置動網格區(qū)域。

根據橋梁加勁梁斷面氣動自激力時程，采用最小二乘法識別薄平板斷面氣動導數。限于篇幅，此處僅給出不同風攻角下的橋梁加勁梁斷面的氣動導數A*1和A*2隨折算風速的變化曲線如圖2所示。

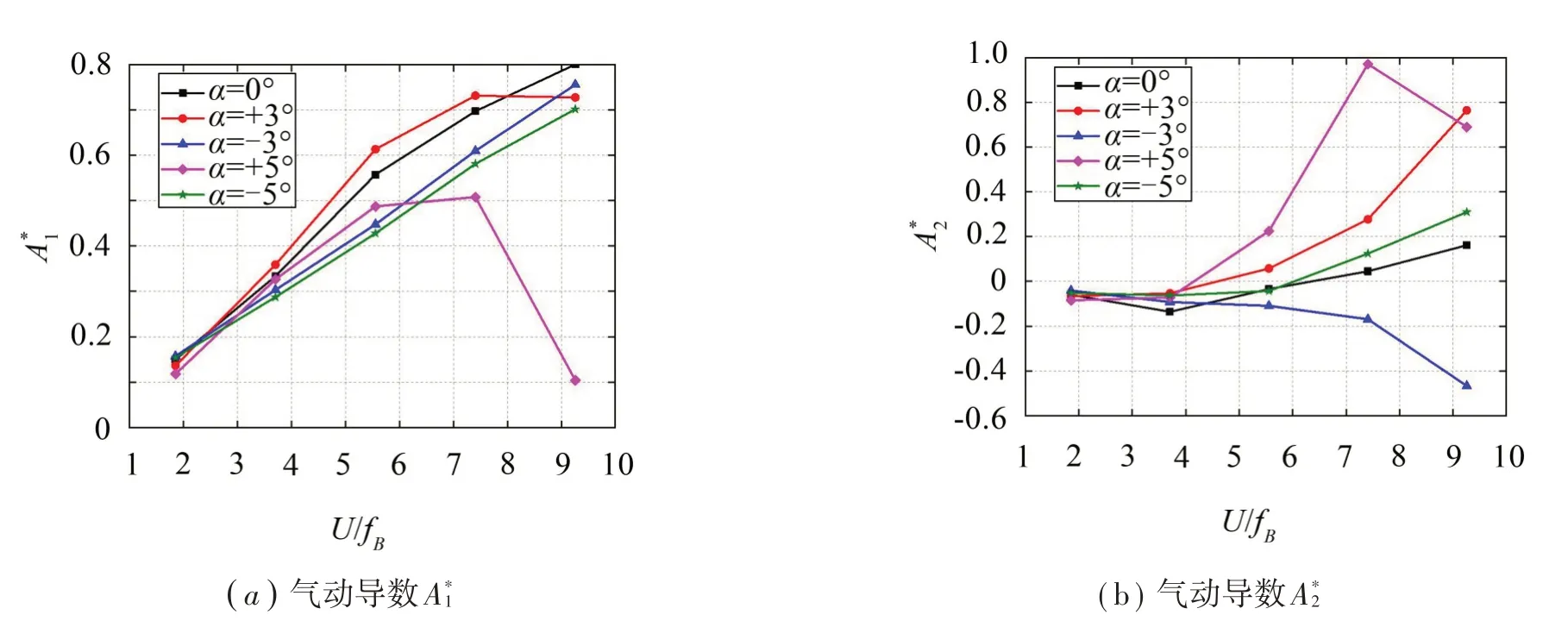
圖2 氣動導數隨折算風速的變化曲線

根據CFD 識別的氣動導數對成橋狀態(tài)結構振型形狀相似的扭彎振型組合進行二維顫振臨界風速分析，得到顫振臨界結果如表4所示。

表4 氣動導數計算的顫振臨界風速/(m?s-1)

(2)流固耦合數值計算

流固耦合是采用CFD 進行橋梁斷面的自由振動計算，可直接得到橋梁斷面的顫振位移響應。幾何縮尺比為λL=1:50，風速比為λV=1:5，動力參數選取扭轉頻率較低的正對稱振型組合。

選取0°、+3°與+5°風攻角進行流固耦合計算，得到不同風速下時程響應曲線，如圖3所示。由圖3可知，0°風攻角下，實橋風速U為55.0 m/s時，振幅劇烈發(fā)散；+3°風攻角下，實橋風速U為45.0 m/s時，振幅劇烈發(fā)散；實橋風速U為35.0 m/s 時，振幅劇烈發(fā)散。

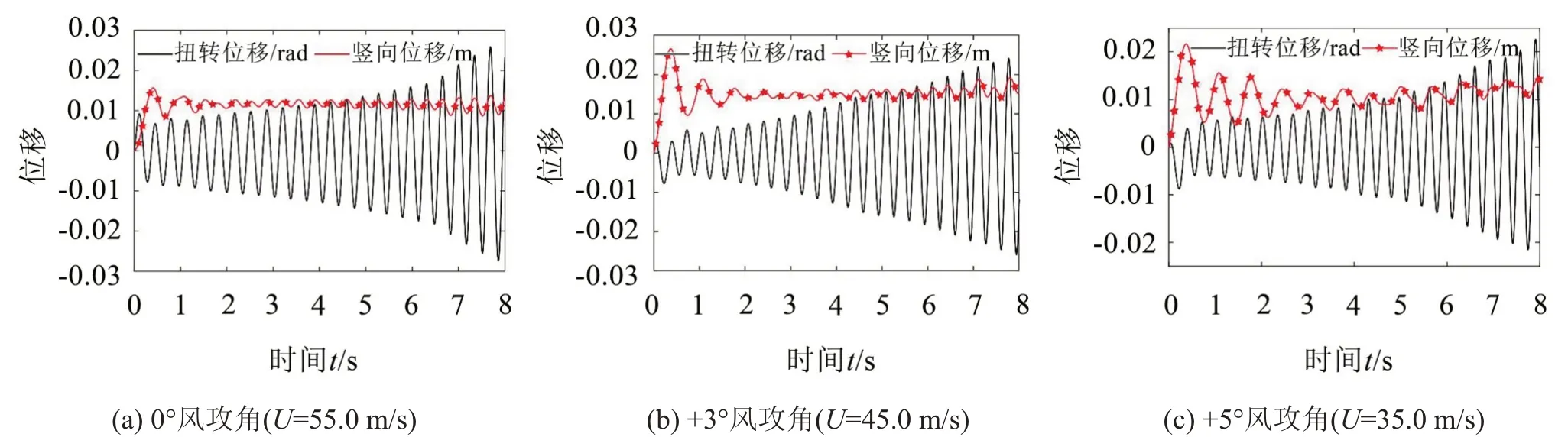
圖3 位移時程曲線

(3)顫振臨界風速對比

根據CFD 識別的氣動導數對成橋狀態(tài)結構振型形狀相似的扭彎振型組合進行二維顫振臨界風速分析，得到顫振臨界風速結果，并將結果與流固耦合計算結果對比，流固耦合計算結果見表5。

表5 流固耦合計算的顫振臨界風速/(m?s-1)

由表4和表5可知，風攻角為0°與+3°時，流固耦合計算結果與氣動導數計算的顫振臨界風速較為一致；風攻角為+5°時，流固耦合計算結果與氣動導數計算的顫振臨界風速差異較大，氣動導數計算的顫振臨界風速結果大于流固耦合結果。

2.2 主梁斷面顫振性能優(yōu)化

根據2.1節(jié)計算結果可知，原始加勁梁斷面顫振穩(wěn)定性不滿足規(guī)范要求，需要進行氣動優(yōu)化。研究表明，設置中央穩(wěn)定板對提高桁架加勁梁懸索橋的顫振臨界風速有明顯作用，故采用中央穩(wěn)定板方案對該橋進行氣動優(yōu)化，具體主梁斷面氣動性能CFD數值模擬優(yōu)化所采用的氣動措施匯總如表6所示。

表6 氣動措施優(yōu)化方案

其中H1和H2分別為上、下穩(wěn)定板高度，分別使用氣動導數和流固耦合兩種方法對表6中所有方案進行計算。顫振臨界風速近似值計算結果如表7所示。

表7 不同方案下顫振臨界風速/(m?s-1)

通過5 種優(yōu)化方案的綜合比較可知，方案1(H1=1.2 m 的上穩(wěn)定板)與方案5（H1=1.4 m 的上穩(wěn)定板）效果總體較好，表明上穩(wěn)定板效果優(yōu)于下穩(wěn)定板。考慮到桁架加勁梁為典型的三維結構，二維CFD數值模擬方法計算結果僅供參考，后續(xù)橋梁顫振穩(wěn)定性將通過主梁節(jié)段模型風洞試驗來進行進一步檢驗，并將重點針對上穩(wěn)定板方案進行研究。

3 風洞試驗

3.1 節(jié)段模型

第2節(jié)從數值模擬的角度探究了復雜山區(qū)大跨度鋼桁梁顫振穩(wěn)定性，該橋處于復雜的山區(qū)風環(huán)境下，且跨度達到千米級，有必要通過風洞試驗對其顫振穩(wěn)定性進行研究。

3.2 節(jié)段模型試驗參數

加勁梁節(jié)段模型試驗參數如表8所示。由表8可以看出，加勁梁節(jié)段模型尺寸、質量、質量慣性矩及頻率均與設計值誤差較小，彈性懸掛系統豎向振動阻尼比為ξh=0.44%，扭轉振動阻尼比為ξa=0.42%，均小于規(guī)范值(0.5%)。

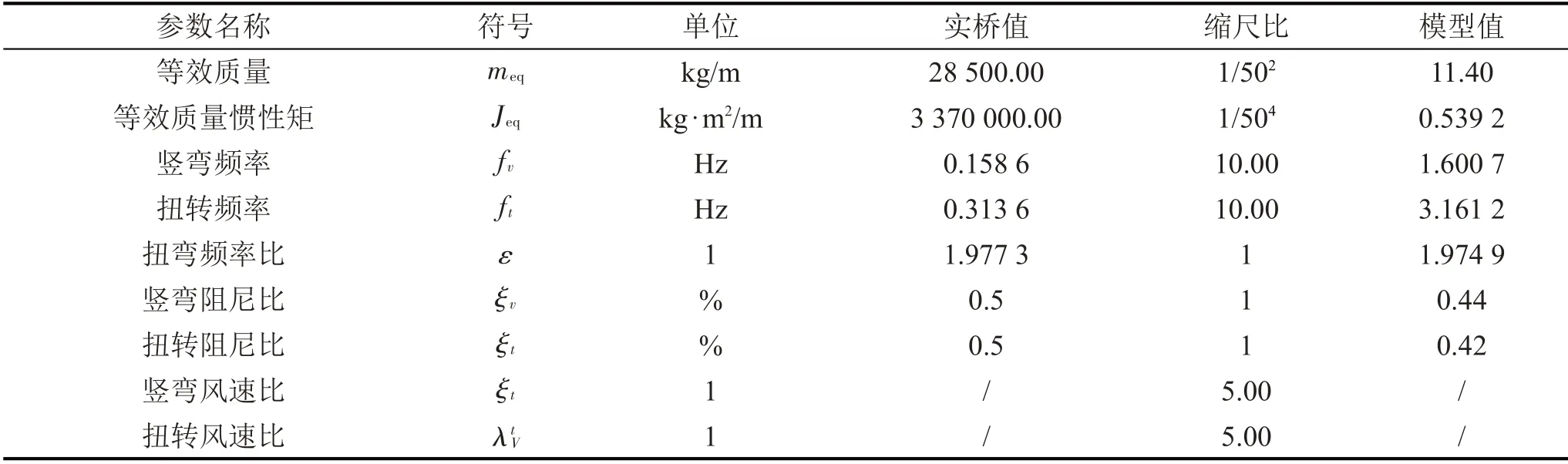
表8 加勁梁節(jié)段模型測振試驗參數

圖4 加勁梁節(jié)段模型

3.3 試驗工況

首先針對原始斷面加勁梁節(jié)段模型，進行風攻角為0o、±3o和±5o時加勁梁節(jié)段模型測振試驗。其次，為提高顫振穩(wěn)定性，采用1.2 m 上中央穩(wěn)定板氣動優(yōu)化方案，進行風攻角為0o、±3o和±5o時加勁梁節(jié)段模型測振試驗。所有試驗工況均在均勻流場下進行，針對原始斷面和1.2 m上中央穩(wěn)定板優(yōu)化后的斷面均進行0o、±3o和±5o風攻角的風洞試驗，共計10個試驗工況。

3.4 顫振穩(wěn)定性試驗結果

限于篇幅，此處僅給出豎向振動和扭轉振動位移響應，如圖5所示。

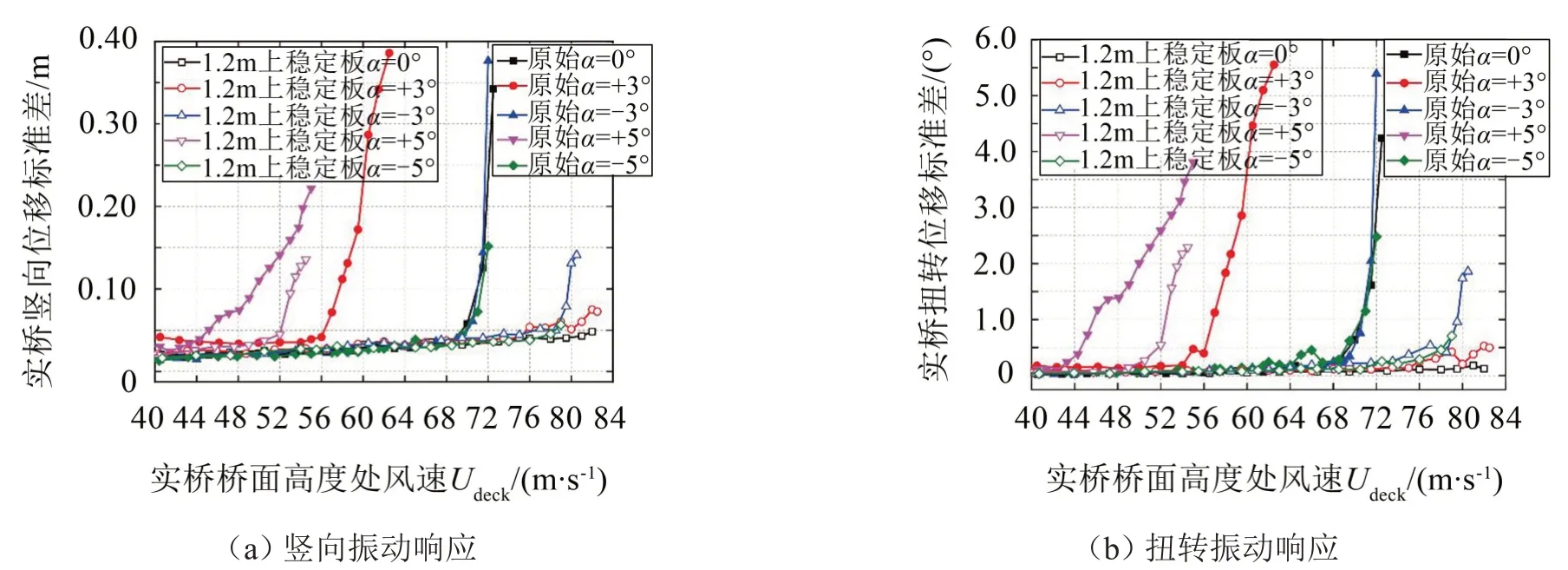
圖5 顫振位移響應

成橋狀態(tài)加勁梁顫振臨界風速如圖6所示。分析圖6可知，原始斷面0°風攻角下顫振臨界風速為68.5 m/s；在0°、-3°與±5°風攻角下，顫振臨界風速大于顫振檢驗風速，在+3°風攻角顫振臨界風速小于顫振檢驗風速，顫振穩(wěn)定性不滿足規(guī)范要求；采用1.2 m上中央穩(wěn)定板優(yōu)化后，顫振臨界風速顯著提高，0°風攻角下顫振臨界風速為82.0 m/s；0°、±3°與±5°風攻角下，顫振臨界風速均大于顫振檢驗風速，顫振穩(wěn)定性滿足規(guī)范要求。

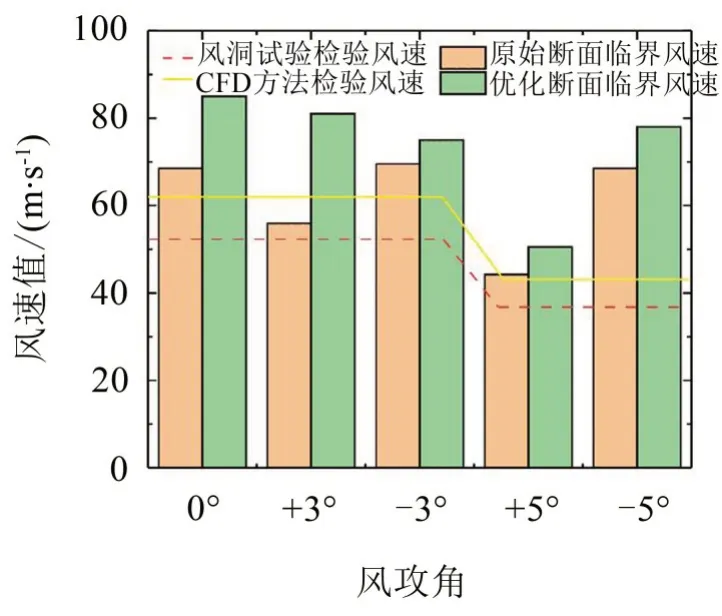
圖6 臨界顫振風速

4 數值仿真與風洞試驗對比

在數值仿真和風洞試驗下的原始斷面和采用1.2 m 上中央穩(wěn)定板氣動優(yōu)化方案的顫振臨界風速見表9，分析表9可知。

表9 數值仿真與風洞試驗結果對比

(1)數值模擬和風洞試驗得到的原始斷面顫振臨界風速均要小于優(yōu)化斷面顫振臨界風速；

(2)數值模擬得到的顫振臨界風速要小于風洞試驗得到的顫振臨界風速。有可能是因為數值模擬在利用氣動導數和流固耦合方法識別顫振臨界風速時具有一定的人為主觀性，為避免該類問題的發(fā)生，應編制相關顫振臨界風速識別程序，這也是后續(xù)要研究的工作。

5 結語

基于CFD 數值模擬和風洞試驗探究了復雜山區(qū)超大跨鋼桁梁懸索橋顫振穩(wěn)定性，主要結論如下：

(1)橋位基本風速U10＝28.0 m/s，橋位處地表類別為D 類,對應的地表粗糙度系數為α0＝0.30；對應的成橋狀態(tài)加勁梁設計基準風速Ud＝37.20 m/s。

(2)風攻角為0°、+3°與+5°時，原始斷面顫振臨界風速小于顫振檢驗風速，不滿足規(guī)范要求。

(3)設置上中央穩(wěn)定板可以明顯提高顫振臨界風速，0°風攻角顫振臨界風速大于70.0 m/s，大于顫振檢驗風速；風攻角為+3°與+5°時，1.2 m 上穩(wěn)定板的顫振臨界風速分別為52.3 m/s 與37.3 m/s，1.4 m上穩(wěn)定板顫振臨界風速分別為56.0 m/s與47.0 m/s。

(4)風洞試驗結果表明：主梁原斷面在0°、-3°與±5°風攻角下，顫振臨界風速大于顫振檢驗風速；在+3°風攻角顫振臨界風速小于顫振檢驗風速，不滿足規(guī)范要求；增設H1=1.2 m上中央穩(wěn)定板后，各試驗攻角下主橋結構顫振臨界風速均大于該橋顫振檢驗風速，顫振穩(wěn)定性滿足規(guī)范要求。