一種更加嚴密的GNSS臺站位移熱彈性效應模型

方 柳 明 鋒 任紅飛

1 地理信息工程國家重點實驗室，西安市雁塔路中段1號，710054 2 西安測繪研究所，西安市雁塔路中段1號，710054

GNSS坐標時間序列中包含各種因素引起的非線性變化，如何定量分析和有效分離不同因素對時間序列非線性變化的影響，是GNSS坐標時間序列分析領域的熱點和難點之一。GNSS坐標時間序列中的非線性變化可分為3類：一是虛假的非線性變化，主要由GNSS數據處理模型不完善或其他系統誤差引起，如GNSS交點年周期誤差、天線相位中心模型誤差等[1-4]；二是真實的基準站非線性運動，如海洋及大氣潮汐、環境負載、基巖及觀測墩熱膨脹效應等[5-8]；三是其他未知因素引起的形變。其中，包括基準站天線觀測墩及其所在基巖在內的熱彈性形變是時間序列中非線性信號的貢獻源之一。

通常情況下，GNSS觀測墩的一端會直接固連在基巖上或具有穩定結構的建筑物頂端，常見的觀測墩材質包括水泥(觀測墩)、鐵(桁架)、鋼(管)、鋁合金(桅桿)等(圖1)。溫度變化對GNSS臺站位移的影響可以分為兩個部分：一是地表溫度變化通過熱傳遞引起的基巖熱膨脹效應，二是GNSS觀測墩溫度變化引起的熱脹冷縮效應[9]。針對基巖受溫度變化產生的位移，目前有兩種分析方法：基于彈性半空間的熱彈性形變模型[10-11]和基于統一的、三維球體的熱彈性形變模型[12]。針對觀測墩的溫度變化，一般的處理方法如下[8]：將空氣溫度變化作為觀測墩內部溫度變化，并且假設觀測墩是一維結構，只存在軸向的形變，溫度變化只引起GNSS天線觀測墩地面以上部分的垂向位移。這種處理方法存在兩個缺陷：一是觀測墩并非一維結構，溫度的變化不僅會引起觀測墩的垂向位移，還會引起水平位移；二是目前的線性模型僅考慮觀測墩地表以上部分的垂向形變，但觀測墩與基巖的熱傳導系數等材料參數并不一致，因此作為一個整體考慮并不符合實際。基于上述理論，利用彈性力學及熱彈性力學相關理論，對軸對稱觀測墩在一維溫度場下的熱彈性問題進行分析建模，得到觀測墩位移的解析解。

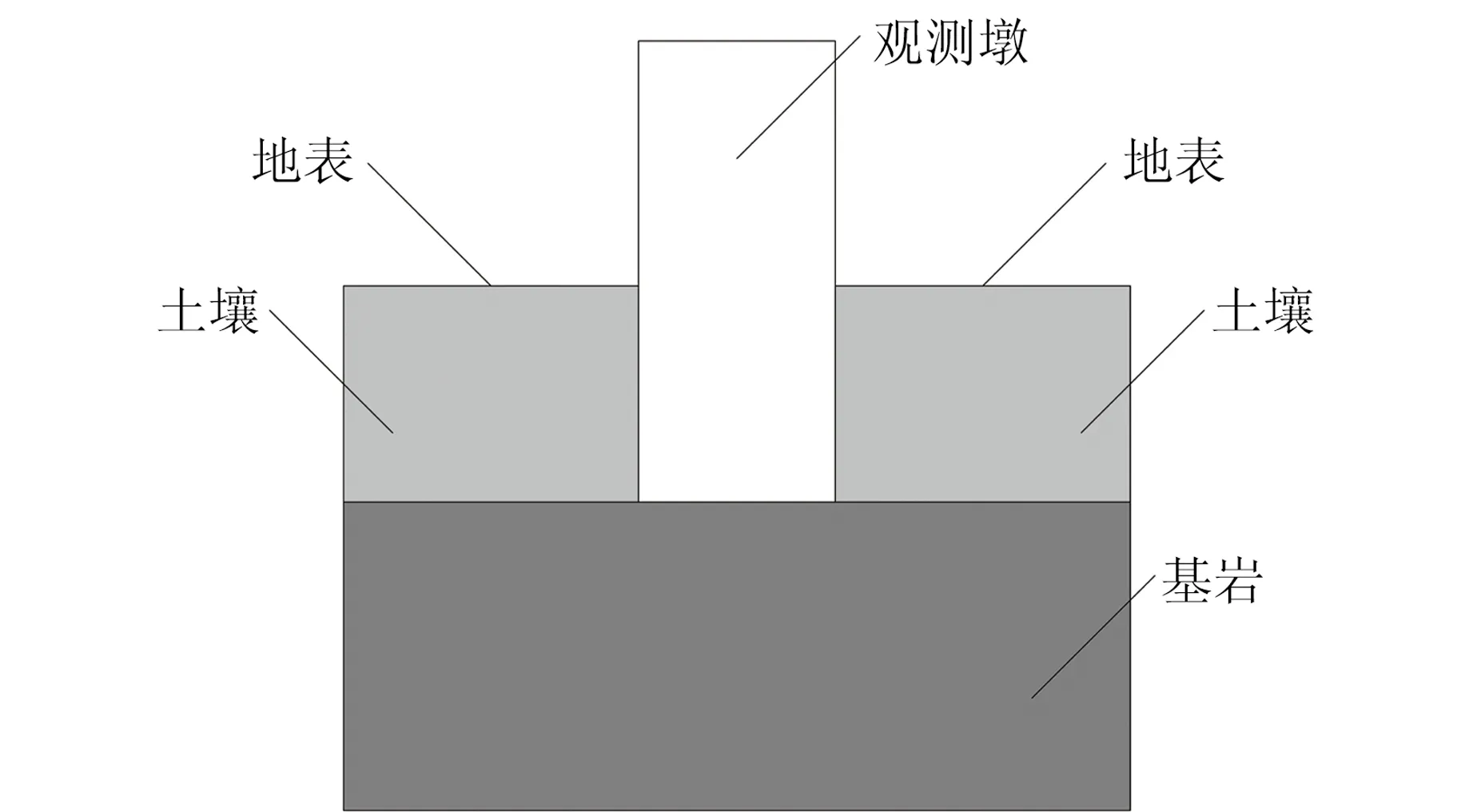
圖1 觀測墩Fig.1 Monument

1 熱彈性形變建模與分析

1.1 基本假定

在進行GNSS臺站位移熱彈性效應建模時，會用到以下彈性力學基本假定[13]：連續性假定、完全彈性假定、均勻性假定、各向同性假定和小變形假定。

1.2 熱彈性形變建模

幾何方程、物理方程和平衡微分方程是彈性力學的3個基本方程，其中幾何方程描述位移和應變之間的關系，物理方程描述應力和應變之間的關系，平衡微分方程描述應力和體力之間的關系。對于圓柱形觀測墩，宜采用柱坐標(r,φ,z)確定空間點的位置(圖2)。

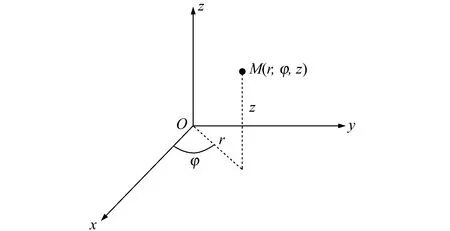
圖2 柱坐標系Fig.2 Cylindrical coordinate system

空間軸對稱的幾何方程為[13]：

(1)

式中，u、w為徑向和軸向的位移，εr、εφ、εz、γzr分別為徑向應變、環向應變、軸向應變和切應變。

空間軸對稱的物理方程為[13]：

(2)

式中，σr、σφ、σz、τzr分別為徑向應力、環向應力、軸向應力和切應力，α為熱膨脹系數，E為彈性模量，μ為泊松比，T為溫度差。

空間軸對稱的平衡微分方程為[13]：

(3)

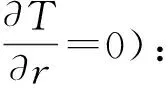
(4)

將觀測墩地表以上部分與地表以下部分分開考慮：

1)對于觀測墩地表以上部分(向上為z軸正方向)，假定地表以上部分觀測墩溫度與地表溫度變化一致(即溫度T是時間的函數，與軸向坐標z和徑向坐標r無關)，則τzr=0，可將式(4)進一步簡化為：

(5)

邊界條件為：

(6)

式中，l1為觀測墩地表以上部分的高度，R為觀測墩半徑。將邊界條件式(6)代入式(5)可得：

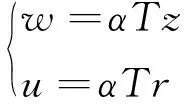
(7)

因此，可得地表以上部分觀測墩產生的垂向位移為：

wabove=αTl1

(8)

2)地表以下部分觀測墩中的溫度隨深度的分布為[14]：

(9)

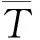
觀測墩地表以下部分的邊界條件為(向下為z軸正方向)：

(10)

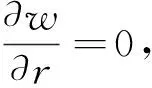
(11)

將式(9)和式(10)代入式(11)，可得方程組的解：

(12)

因此，地表以下部分觀測墩產生的位移為：

(13)

2 模型結果對比

彈性半空間模型分析得到的基巖垂向位移[8]為：

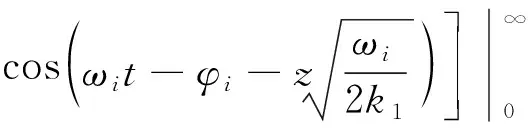
(14)

式中，μ1、α1、k1分別為基巖的泊松比、熱膨脹系數和熱擴散系數。

(15)

(16)

文獻[8]中，觀測墩頂端的垂向位移為觀測墩地表以上部分位移wabove與基巖位移wbedrock的和：

(17)

由式(16)和式(17)可知，本文得到的觀測墩地表以上部分的垂向位移與文獻[8]的結果一致。對于觀測墩地表以下部分，文獻[8]中是將觀測墩與基巖作為一個整體考慮，忽略了觀測墩與基巖的熱擴散系數、熱膨脹系數和泊松比等參數的不一致，因此將觀測墩地表以下部分與基巖分開考慮會更符合實際。此外，文獻[8]還忽略了觀測墩的水平位移，由于水平位移會隨半徑的增大而增大，因此需要將接收機安裝在圓心處以消除水平位移對結果的影響。

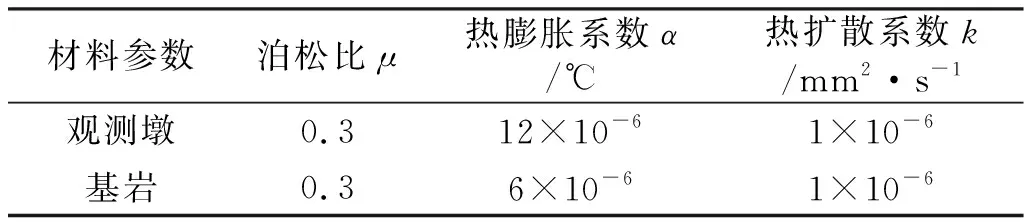
表1 材料參數

圖3 總位移與溫度隨時間的變化Fig.3 Vertical displacement and temperature varied with time

圖4 本文模型與文獻[8]模型基巖位移對比Fig.4 The comparison of the bedrock displacement between the models in this paper and the literature [8]

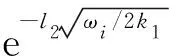
圖5和圖6分別為本文模型與文獻[8]模型地表以下總位移和整體總位移對比，本文模型地表以下總位移和整體總位移分別比文獻[8]的結果大55.1%和24.2%。這是因為本文模型中觀測墩頂端的垂向位移為觀測墩地表以上部分位移、地表以下部分位移和基巖部分位移之和，而文獻[8]中觀測墩頂端的垂向位移僅為觀測墩地表以上部分位移與基巖位移之和。由于觀測墩的熱膨脹系數(12×10-6/℃)比基巖的熱膨脹系數(6×10-6/℃)大，因此文獻[8]中將觀測墩與基巖作為一個整體會使總位移偏小。

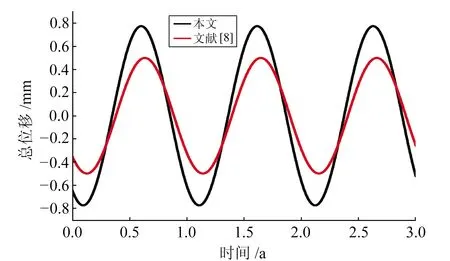
圖5 本文模型與文獻[8]模型地表以下總位移對比Fig.5 The comparison of vertical underground displacement between the models in this paper and the literature [8]

圖6 本文模型與文獻[8]模型總位移對比Fig.6 The comparison of vertical displacement between the models in this paper and the literature [8]

3 結 語

本文基于彈性力學及熱彈性力學的相關理論，通過公式推導對軸對稱觀測墩在一維溫度場下的熱彈性問題進行建模與分析，提出一種更加嚴密的熱彈性模型，用于計算觀測墩位移。結果表明：

1)觀測墩的垂向位移由觀測墩及基巖的泊松比、熱膨脹系數、溫度差和高度共同決定。

2)本文提出的改進模型中觀測墩頂端的垂向位移為觀測墩地表以上部分位移、地表以下部分位移和基巖部分位移之和，考慮了觀測墩與基巖材料參數的不同，相對于文獻[8]模型更符合實際，因此能更準確地估算熱彈性效應對GNSS臺站位移的影響。