上海沿海站點極大風速預報方程的細化和完善

朱智慧，鄭運霞，過霽冰

（1.上海海洋中心氣象臺，上海 201306；2.中國氣象局上海臺風研究所，上海 200030；3.上海市奉賢區氣象局，上海 201416）

1 引言

大風災害嚴重威脅航運、港口、海上石油平臺和郵輪等的作業安全[1-3]。作為中國沿海最大城市，上海有豐富的港口航道、濱海旅游和海洋能源等資源，海洋運輸業、船舶制造業和濱海旅游業等處于全國領先地位。上海地處江海陸交界處，地形復雜，海上大風頻發，也是我國受大風天氣災害影響較為顯著的海域之一。隨著海洋經濟的發展，沿海大風預報精細化和準確性的需求也越來越大。

日常海洋氣象業務中，海上大風預報主要依靠數值模式的風預報產品[4-5]。部分研究基于數值預報產品，利用概率密度匹配[6]、主成分分析[7]、神經網絡[8-9]和K最近鄰算法[10]等方法建立了沿海大風的預報方法。數值模式預報的風為平均風，而沿海作業更關心極大風速能達到多少[11]，數值模式缺少對應的預報產品，根據平均風來預報極大風主要依靠預報員的主觀分析，缺少客觀量化的預報技術。因此，建立上海沿海精細化極大風速預報方程，對于提高沿海大風預報能力，避免或減輕大風災害的影響具有重要意義。一些研究分析了10 min 平均最大風速與極大風速的關系，發現兩者存在近似線性的關系[12]。基于測風塔數據的研究也表明，在近地面層中，最大風速和極大風速普遍具有較好的線性關系[13]，但直接建立2 min平均風速和極大風速關系的研究依然較少。針對上海沿海極大風速預報技術已開展了初步研究[14]，但該研究只使用了3 個浮標站1 a 左右的數據，站點數量和觀測數據都偏少，而且浮標站靠近外海，不能代表沿岸海域的情況。隨著海洋氣象預報業務精細化要求的不斷提高，有必要對上海沿海站點的極大風速預報方程進一步細化。因此，本文利用上海沿海14個觀測站點的觀測資料，重新建立了從沿岸到近海各站點極大風速預報方程，為利用數值模式預報的平均風速進行上海沿海精細化極大風速預報奠定了基礎。

2 資料與方法

2.1 資料

本文使用的資料為上海沿海14個站點的觀測資料，14個站點包括10個岸基站（省級氣象觀測站）和4個浮標/船標站。資料時間段為2012 年1 月1 日—2019 年12 月31 日，時間間隔為1 h。觀測要素為2 min平均風速和極大風速。14個站點的分布見圖1。

圖1 站點分布圖Fig.1 Map of sites distribution

本研究將14 個站點的原始觀測數據分為兩個時間段的數據集：2012 年1 月1 日—2018 年12 月31日為建模時間段，這部分數據用來建立極大風速預報方程；2019 年1 月1 日—12 月31 日為檢驗時間段，這部分數據作為獨立樣本來檢驗極大風速預報方程的應用效果。剔除缺測和錯誤數據，14 個站點的總樣本數、建模時間段樣本數和檢驗時間段樣本數見表1。

表1 14個站點的樣本數Tab.1 Sample number of 14 stations

2.2 方法

本文分析2 min 平均風速、回歸極大風速和觀測極大風速關系時，使用的檢驗統計量為相關系數和平均絕對誤差。

本文使用的建模方法有兩種：線性回歸分析和人工神經網絡。

（1）線性回歸分析：設y為極大風速，x為2 min平均風速，x，y的關系由一元線性回歸方程確定，即：

式中，a0和a1統稱為回歸方程的參數。a0是回歸方程的常數項，也是回歸直線在y軸上的截距；a1是回歸系數，也是回歸方程的斜率。

（2）人工神經網絡：本文采用標準的反向傳播（Back Propagation，BP）網絡[15]，由3 個神經元層次組成，即輸入層、隱層和輸出層。其訓練函數為最速下降BP 算法。選擇人工神經網絡結構時，采用了1個隱層、2個節點的建模方案，輸入層為2 min平均風速，輸出層為極大風速。

3 結果分析

利用14個站點建模時間段的觀測數據，基于回歸分析方法，得到了各站點的2 min 平均風速和極大風速回歸方程，這14 個站點的2 min 平均風速和極大風速回歸方程如下：

y= 1.52x+ 1.64（新河）

y= 1.44x+ 1.46（海灣七五一）

y= 1.53x+ 1.63（長興郊野公園）

y= 1.33x+ 1.86（海灣五四）

y= 1.30x+ 2.11（三甲港）

y= 1.56x+ 1.55（中興）

y= 1.25x+ 2.23（老港固廢基地）

y= 1.28x+ 1.51（滴水湖入海閘）

y= 1.25x+ 1.32（東灘濕地）

y= 1.23x+ 2.50（洋山站）

y= 1.03x+ 0.46（長江口燈船）

y= 1.04x+ 0.40（黃澤洋燈船）

y= 1.03x+ 0.57（口外浮標）

y= 1.05x+ 0.39（海礁浮標）

14 個站點的回歸極大風速、BP 神經網絡預報極大風速與觀測極大風速的誤差分析見表2。表中可見，兩種建模方法得到的14 個站點的極大風速y與觀測極大風速的平均絕對誤差都較小，在1.34 m/s以下，而且對于每個站點，兩種建模方法的平均絕對誤差值十分接近，這說明回歸分析方法和BP 神經網絡方法都能較好地應用于極大風速的業務預報。此外，從表中也可以看到，在受地形影響較小的海面，兩種建模方法的誤差更小。

表2 建模時間段回歸極大風速、BP神經網絡預報極大風速與觀測極大風速平均絕對誤差（單位：m/s）Tab.2 Average absolute error between regression maximum wind speed,BP neural network predicted maximum wind speed and observed maximum wind speed in modeling time period（unit:m/s）

BP神經網絡作為一種有效的建模方法，在很多領域得到了應用。但這種方法也存在一些缺點和不足，主要表現為：學習過程收斂速度慢、效率低和學習率不穩定等。相比之下，利用線性回歸方法建立的極大風速預報模型簡捷高效，作為日常業務應用技術更合適，因此，本文后面的研究使用的是線性回歸分析模型。

各站點a1的空間分布見圖2。圖中可見，各站點a1從沿岸到近海基本呈遞減趨勢，a1最大的站點在長江口和杭州灣內，最小的站點為沿海4 個浮標站。這說明在上海沿岸水域，2 min平均風速和極大風速的關系不是均一的分布。這種不均一的分布可能與地形對陣風的增強作用有關，這與前人研究一致[16]。此外，對比前期利用3 個浮標站得出的研究結果[14]可以發現，從沿岸到近海的不同站點建立獨立的回歸方程，才能滿足沿岸精細化大風預報的需求。

為了分析不同風級的2 min 平均風速和極大風速的關系，本文按2 min 平均風速將14 個站點的風力分為0～9 級，分別進行了回歸分析（10 級以上樣本極少，因此本文未做統計分析）。以圖2中a1大小不同的區域為依據，選取海礁浮標、東灘濕地、三甲港和海灣七五一4 個站點為代表進行分析，不同風級a1和a0的大小見圖3。圖中可見，4個站點4級以上平均風力，a1和a0大小基本保持不變，這說明，2 min 平均風速和極大風速保持穩定的線性關系。對于離海岸較遠的海礁浮標而言，平均風力4 級以下的回歸系數與4 級以上相比數值變化很小，而沿岸站點東灘濕地、三甲港和海灣七五一的回歸系數變化較大，尤其是長江口區的東灘濕地站點，兩個回歸系數都有較大變化，這可能與較小的風受地形影響較大有關。

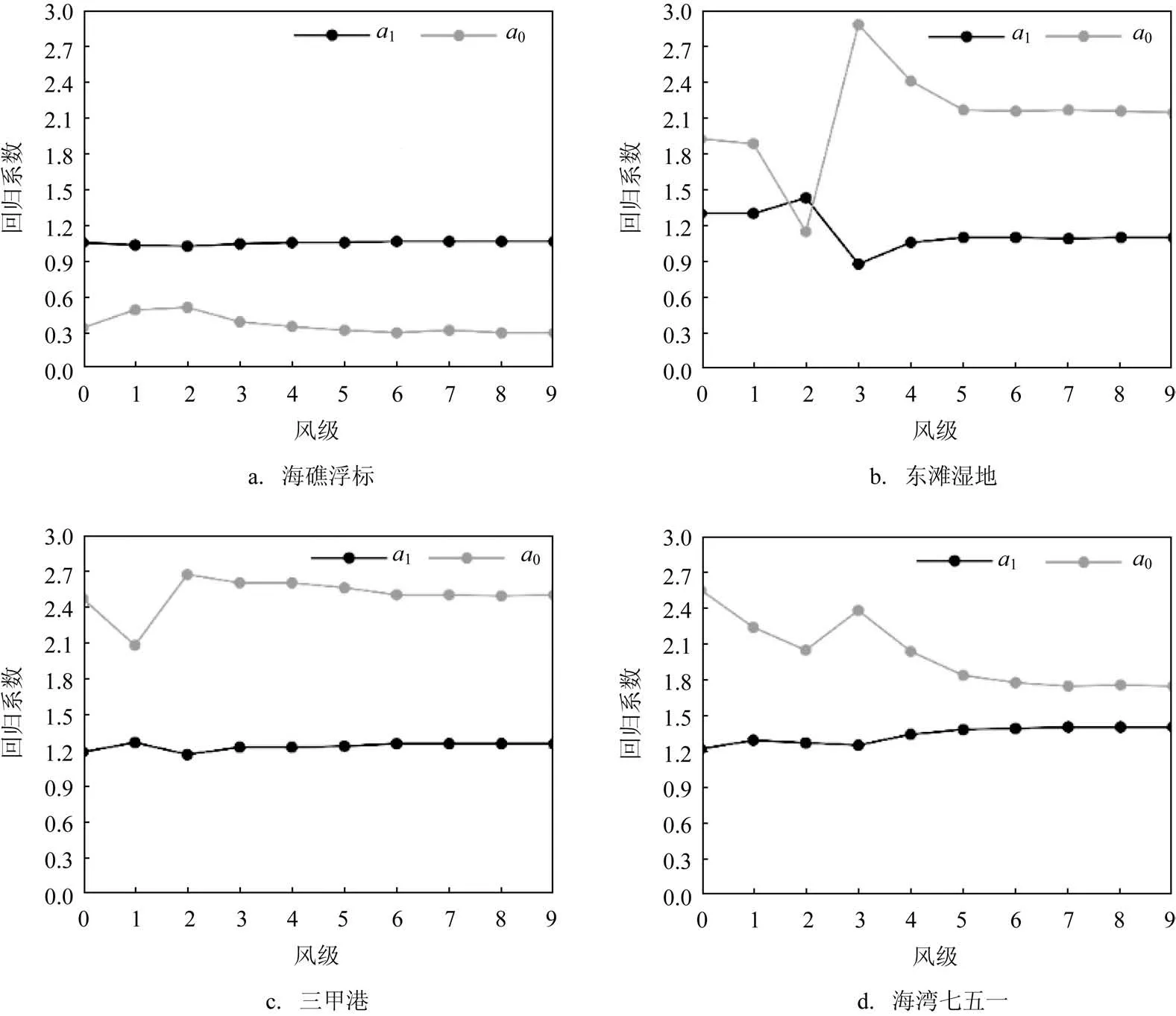
圖3 不同風級回歸系數a1和常數項a0的大小Fig.3 Regression coefficients a1 and constant terms a0 of different wind levels

以2019 年觀測數據作為獨立樣本，分析各站點回歸方程的有效性。基于建立的各站點回歸方程，首先計算回歸極大風速y，然后與觀測極大風速yobs進行相關性分析和誤差分析，結果見表4。表中可見，14 個站點的y和yobs相關性都在0.82 以上，通過了顯著水平α= 0.01 的顯著性檢驗，同時也可以看到，越靠近外海，兩者的相關性越好。14個站點的y和yobs的平均絕對誤差較小，絕大部分在2 m/s以下，這也說明建立的極大風速回歸方程能夠較好地估計各站點的極大風速。

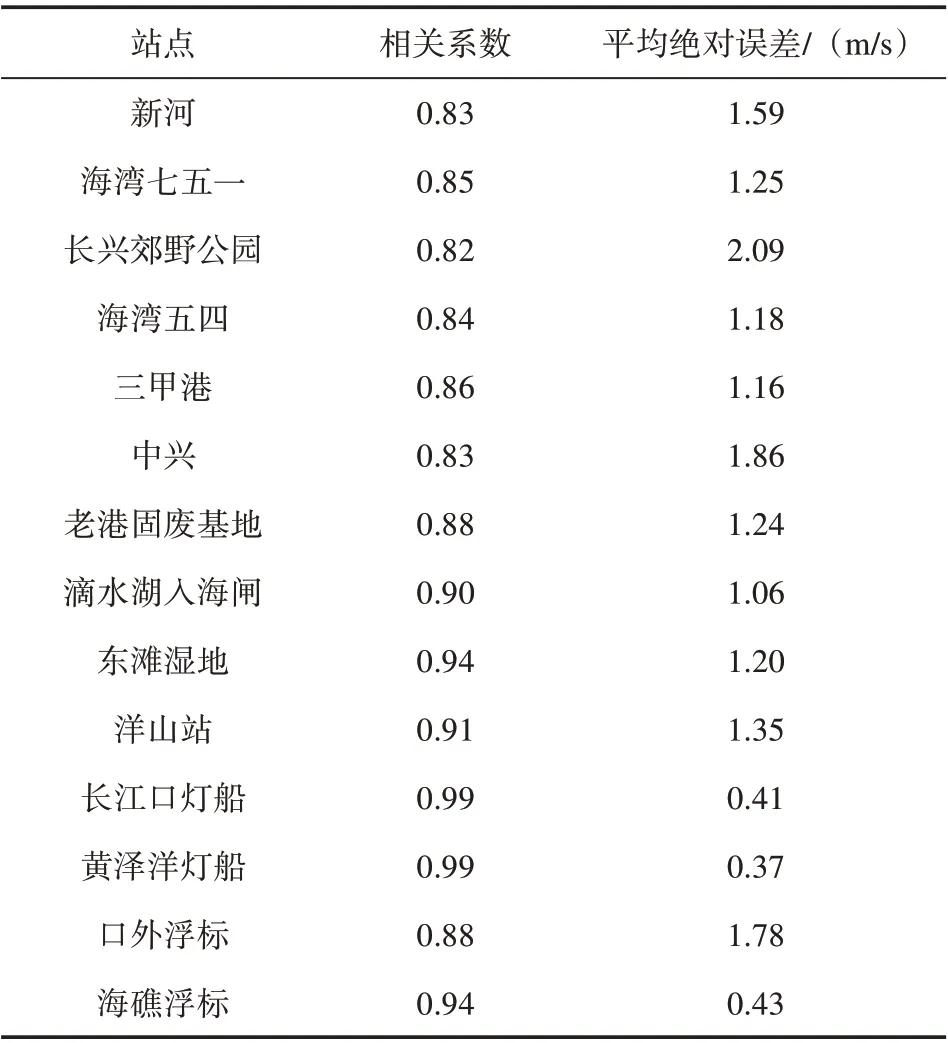
表4 檢驗時間段回歸極大風速與觀測極大風速相關性和誤差分析Tab.4 Correlation and error analysis between regression maximum wind speed and observed maximum wind speed in test time period

臺風對沿海影響極大，在日常預報業務中，準確預報臺風極大風速還缺乏十分有效的方法。為了分析臺風2 min 平均風速與極大風速是否存在獨特的關系，本文選取了2012—2019年影響上海沿海的15 個臺風個例，使用平均風力在7 級以上時次的數據進行了2 min 平均風速和極大風速的回歸分析。臺風基本信息見表5。

表5 2012—2019年影響上海沿海的臺風基本信息Tab.5 Basic information of typhoons affecting Shanghai coast from 2012 to 2019

如果站點的臺風大風次數和樣本數較少，則建立的回歸方程的可信度不高，因此本文只選取了2012—2019 年臺風大風（平均風力在7 級以上）樣本數在80 個以上的5 個站點進行了回歸分析，選取的站點和樣本數信息見表6。這5 個站點在臺風影響期間的2 min 平均風速和極大風速回歸方程如下：

表6 進行臺風極大風速回歸分析的站點和樣本數Tab.6 Number of stations and samples for regression analysis of typhoon maximum wind speed

y= 1.15x+ 1.49（滴水湖入海閘）

y= 1.14x+ 1.37（東灘濕地）

y= 1.05x+ 0.38（長江口燈船）

y= 0.98x+ 1.52（黃澤洋燈船）

y= 1.06x+ 0.22（海礁浮標）

對比5個站點在臺風影響期間的回歸方程和利用建模時間段所有數據建立的回歸方程可以看到，兩組方程的a1和a0變化不大，說明盡管臺風影響期間風力較大，2 min平均風速和極大風速的關系并沒有特別的變化，利用建模時間段所有數據建立的回歸方程同樣適用于臺風大風預報。臺風影響期間y與yobs的相關性和誤差分析見圖4，圖中可以看到，利用回歸方程得到的兩者的相關性都在0.64 以上，通過了顯著水平α= 0.01 的顯著性檢驗，說明建立的方程能較好地反映臺風影響期間2 min 平均風速和極大風速的關系。此外，靠近外海的浮標/燈船站的相關系數都在0.92 以上，遠高于沿岸站點，平均絕對誤差也在0.7 m/s以下，說明臺風極大風同樣受到地形的顯著影響，在地形影響越小的區域，臺風大風的回歸效果越好。

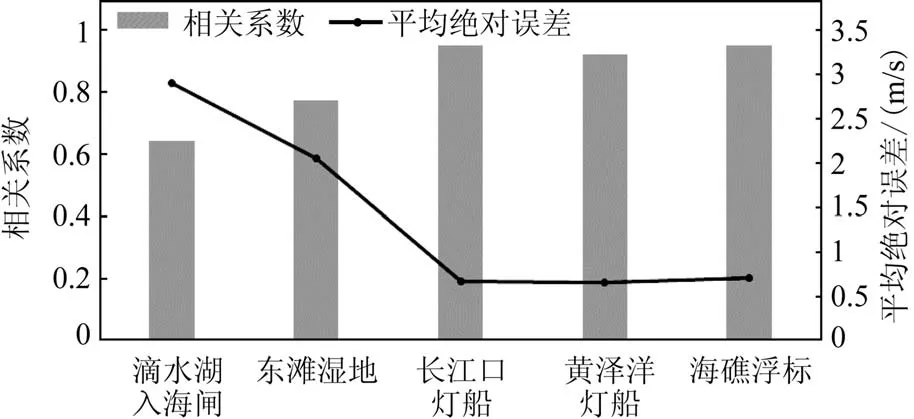
圖4 臺風影響期間5個站點回歸極大風速與觀測極大風速相關性和誤差分析Fig.4 Correlation and error analysis between regres-sion maximum wind speed and observed maximum wind speed at five stations during the period of typhoon influence

4 結論與討論

本文利用上海沿海14個站點的觀測資料，對沿海站點的極大風速預報方程進行了細化和完善。主要結論如下：

（1）在上海沿海水域，2 min 平均風速和極大風速的關系不是均一的分布，各站點的回歸系數a1從陸地到近海基本呈遞減的趨勢。在受地形影響較小的海面，回歸極大風速與觀測極大風速的相關性更好，平均絕對誤差更小，能夠更好地反映2 min 平均風速和極大風速的關系。通過對沿海站點極大風速預報方程進行細化，可以滿足日常海洋氣象精細化業務預報的需求。

（2）上海沿海各站點在4 級以上平均風下，2 min平均風速和極大風速的關系基本保持不變，回歸系數不會因風力變大發生較大變化。

（3）2019 年獨立樣本的檢驗結果表明，建立的各站點極大風速回歸方程能夠較好地估計站點的極大風速。

（4）挑選臺風影響期間的大風樣本進行分析，可以發現，上海沿海建模時間段的2 min 平均風速和極大風速回歸方程基本一致，不存在特殊的回歸關系，建模時間段建立的極大風速預報方程可以作為通用方程在日常預報業務中應用。此外，臺風極大風同樣受到地形的顯著影響，在地形影響越小的區域，臺風極大風速的回歸效果越好。