基于改進ESO的磁懸浮系統模型參考滑模控制

胡 坤，蔣慶楠，季晨光，楊 健，李 飛

（1.安徽理工大學深部煤礦采動響應與災害防控國家重點實驗室，安徽 淮南 232001；2.安徽理工大學機械工程學院，安徽 淮南 232001）

帶式輸送機是重要的散料運輸設備之一，被廣泛應用于煤炭、化工、物流等領域的物料運輸中。傳統的帶式輸送機依靠托輥支撐輸送帶和物料。在其運行過程中，托輥與輸送帶發生擠壓接觸而造成的能耗約占輸送機系統總能耗的70%［1］。為了降低能耗，提高輸送機的經濟性能，將磁力支撐系統代替原有的承載托輥組形成磁懸浮輸送機已經成為一種新的研究方向。在磁懸浮技術的應用研究中，實現輸送帶和物料的穩定懸浮且具有良好的抗干擾能力是關鍵所在。因此，磁懸浮控制方法得到了廣泛的關注。

懸浮系統具有開環不穩定性、非線性和時變性等，即使其在工作點具有線性化特點，但仍然是一個三階不穩定系統。因此必須采用適當的控制方法來實現磁懸浮輸送機的穩定運行。近幾十年，國內外學者提出了一系列磁懸浮系統穩定性控制方法［2-6］，常用的有狀態反饋控制、PID（proportion-integral-differential，比例-積分-微分）控制、最優控制、魯棒控制和模型預測控制等。這些控制方法都基于精確的磁懸浮系統模型，然而在實際的磁懸浮系統數學建模時存在著未建模動態和未知擾動的影響，并不能得到精確的磁懸浮系統模型，因此磁懸浮系統穩定控制方法的設計存在著一定的難度。

20世紀50年代發展起來的滑模變結構因結構簡單，易于實現，對不確定性干擾具有良好的魯棒性等特點［7，9］，被廣泛應用于各種控制對象中。如：Shieh等［10］根據磁懸浮系統的測量氣隙，設計了滑模控制方法，減小了系統的不確定性對系統性能的影響，提高了磁懸浮系統的魯棒性，但未能很好地解決系統抖振現象；劉春芳等［11］采用模糊滑模控制方法，根據電磁懸浮系統的動態非線性數學模型，設計了系統滑模面，通過等效控制和切換控制實現了對參數攝動和外部擾動的完全魯棒性，但模糊規則的建立需要很豐富的專家經驗，這對磁懸浮輸送帶的控制具有一定的難度。

近年來，觀測器理論發展迅速，其在狀態與干擾未知的系統中得到了廣泛的應用。如：申永鵬等［12］將擴展滑模觀測器用于永磁同步電機無位置傳感器的控制，比傳統滑模觀測器更能消除系統的抖振，并且觀測精確度受轉速變化的影響較小，系統具有更高的觀測精確度和更好的動態性能，并經實驗證明，通過選擇合適的觀測器可以有效估計傳感器測量帶來的誤差以及未知的外部干擾。觀測器與控制器相結合的控制方法已經得到了越來越多的應用［13-17］。因此，利用基于干擾觀測器的滑模控制方法來消除磁懸浮系統的抖振和干擾將成為可能。

筆者基于改進的永磁-電磁混合U型電磁鐵模型，提出一種基于非線性擴張狀態觀測器（extend state observer，ESO）的模型參考改進滑模控制策略。首先，將改進的冪次趨近律應用于滑模控制，對參考模型進行軌跡跟蹤設計；其次，針對狀態方程的非匹配不確定項和未知外部干擾，利用非線性ESO進行觀測，將觀測到的干擾對系統進行補償，以減小系統的抖振，增強系統的魯棒性能；最后，通過仿真分析來驗證該方法的魯棒性和優越性。

1 磁懸浮輸送帶的動力學模型

1.1 磁懸浮輸送帶的工作原理及電磁結構

磁懸浮帶式輸送機的結構如圖1所示。其中磁懸浮系統主要由混合電磁鐵、輸送帶、導磁體懸掛裝置、限位滾輪、機架和托輥組組成。該系統由混合電磁鐵提供的磁力吸引導磁體懸掛裝置從而使輸送帶懸浮起來，使其脫離托輥組的支撐；限位滾輪防止輸送帶左右移動引起的跑偏，兩端的驅動滾筒提供縱向驅動力使輸送帶縱向移動；通過調節電磁鐵電流的大小和方向來改變電磁力，當電磁力與輸送帶和物料所受重力相等時，輸送帶與輔助托輥不再接觸，從而消除了摩擦力及摩擦帶來的能耗。

圖1 磁懸浮帶式輸送機的結構Fig.1 Structure of magnetic levitation belt conveyor

混合電磁鐵的結構和布置將直接影響輸送機電磁力的大小及其控制系統的設計。永磁體在電磁鐵中的安裝方式有2種：一種是將永磁體安裝在鐵芯中間，這樣永磁體可以得到很好的保護，但是其接觸面積受到了限制［18］；另一種是將永磁體安裝在電磁鐵磁極的兩端，這樣雖然磁路長度可以不受限制，但是永磁體離懸浮物很近而得不到很好的保護［19］。綜合輸送帶的應用環境，設計的永磁-電磁混合電磁鐵結構如圖2所示。將永磁體安裝在鐵芯中間，并使永磁體與磁路的接觸面積得到擴大，以提供更大的永磁力并且可以得到很好的保護；同時，在電磁鐵磁極兩端增大氣隙接觸面積，以提供更大的磁吸力，而且這種T形翼緣可以提高電磁鐵極板的剛度［20］，也使得電磁鐵的線圈不會輕易碰到懸浮物。

圖2 永磁-電磁混合電磁鐵的結構Fig.2 Structure of permanent magnet-electromagnetic hybrid electromagnet

1.2 永磁-電磁混合電磁鐵的數學模型

根據等效磁路法求永磁-電磁混合電磁鐵的動力學模型。設電磁鐵兩極的線圈匝數均為N/2，磁鐵與導磁體之間的氣隙為z（t），線圈的電壓為u（t），線圈的電流為i（t），永磁體的厚度為hpm，永磁體與磁路接觸的有效面積為s1，永磁體的矯頑力為Hc，永磁體的導磁率為μ，混合電磁鐵的總質量為m，重力加速度為g，電磁鐵磁極面積為s2；并作出如下假設：

1）忽略電磁繞組和永磁體的漏磁通；

2）磁力線簡化為直線和圓弧線，并忽略磁路飽和；

3）忽略導磁體和鐵芯的磁阻。

求解得到磁懸浮結構對導磁體的電磁力F（z，i）為：

式中：μ0為空氣磁導率；μr=μ/μ0，為永磁體的相對磁導率。

電磁鐵繞組回路的電壓方程為：

式中：R為電磁鐵電阻；Nn為電磁鐵匝數；Φ(z，i)為氣隙磁通。

對電磁鐵進行受力分析，可得其動態模態方程組為：

式中：f（t）為外界干擾量；（z0，i0）為系統狀態平衡點。

將式（1）在系統狀態平衡點（z0，i0）處進行泰勒展開，線性化后代入方程組（3），可得：

以電壓作為輸入變量，磁懸浮氣隙為輸出變量，選擇(Δz，Δz˙，Δi)T作為狀態變量，可得到如下狀態方程：

1.3 磁懸浮系統開環模型

由式（4）的力學和電壓方程可以得到以電壓為控制輸入、氣隙為控制輸出的磁懸浮開環系統傳遞函數：

由勞斯判據可知該開環系統具有不穩定性，且是一個三階不穩定系統。為了降低系統模型的階數，引入電流反饋，以電磁鐵線圈繞組的電流為控制輸入量，氣隙為輸出量，建立具有電流反饋的磁懸浮開環系統，如圖3所示。其中：ka為功率放大器增益系數，ky為傳感器增益系數。

圖3 具有電流反饋的磁懸浮開環系統Fig.3 Magnetic levitation open-loop system with current feedback

由圖3可以得到新的磁懸浮開環系統傳遞函數：

根據式（7）可知，雖然通過加入電流反饋降低了系統模型的階數，但系統仍然具有不穩定性。因此，對磁懸浮開環系統進行控制器的設計，以增強其穩定性。

2 磁懸浮系統控制器的設計

2.1 控制器總體設計

磁懸浮系統控制器的設計如圖4所示。其中，磁懸浮系統參考模型的輸入um是基于滑模控制器（sliding mode control，SMC）設計的，使得參考模型能夠輸出一個無干擾和不確定因素的參考氣隙信號xm。該輸出信號更加連續，更容易被磁懸浮系統跟蹤，也更加具有穩定性。新型滑模控制器基于參考模型的輸出和改進ESO進行設計，其中ESO用于對系統未建模動態和未知干擾進行估計，將估計的狀態加入滑模控制器，使滑模控制器具有較好的魯棒性。同時，將估計的干擾d^補償到控制律中，以改善控制系統的動態性能。

圖4 磁懸浮系統控制器的設計Fig.4 Design of magnetic levitation system controller

2.2 參考模型及控制器設計

磁懸浮參考模型的設計直接影響到滑模控制的狀態跟蹤問題，以x=(Δz，Δz˙)T為狀態，電流為輸入，氣隙變化量為輸出，建立磁懸浮系統的參考模型：

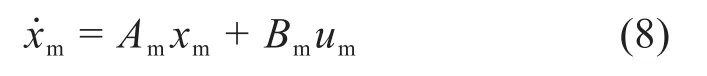
式中：Am、Bm均為參考模型的標準值。

針對參考模型（8），設計滑模面s為：

式中：c為大于0的常數；xr和x˙r分別為給定的氣隙間距及其導數；xm1-xr為氣隙的跟蹤誤差，記 xm2=x˙m1。

采用削弱抖振的指數趨近律設計參考模型的控制律：

式中：ζ、k均為常數，ζ＞0,k＞0。

結合式（8）可得參考模型的控制律為：

式中：am3、am4和bm2均為常數，可由磁懸浮系統模型求出。

2.3 基于新型趨近律的滑模控制器設計

為了削弱磁懸浮系統的抖振，根據磁懸浮系統狀態距滑模面的距離設計不同的趨近速度，故在冪次趨近律和指數趨近律的基礎上采用分段函數的形式設計滑模控制的趨近律。設計的新型滑模趨近律為：

式中：k1，k2，k3，k4，λ均為大于零的常數，?＞1，0＜β＜1，并且所有參數可調；x2為系統的狀態變量。

當系統的運動點進入滑模狀態時，采用Lyapunov穩定性理論來求證系統的穩定性。由新型分段趨近律的設計可知，新型趨近律是冪次趨近律與等速趨近律的組合形式，故Lyapunov函數的導數˙恒滿足：

可見新設計的趨近律可以滿足漸進穩定的要求。

在新型趨近律的基礎上，滑模控制器的滑模面設計為：

式中：b2為控制輸入系數；a21為磁懸浮系統狀態方程x1的系數。

式（16）是在未考慮未建模動態和外部干擾的情況下得出的，會影響滑模控制器輸出的準確性，故須對系統狀態和干擾進行估計。

3 改進ESO設計及估計誤差分析和實時補償

針對所求的磁懸浮系統模型存在著未建模動態和未知干擾的影響，采用ESO對系統狀態和未知干擾進行估計，并將估計的狀態加入所設計的新型滑模控制器中，對估計的干擾進行系統補償，以減小系統不確定性帶來的影響，進而提高系統的魯棒性。

3.1 ESO設計

磁懸浮系統狀態方程為：

式中：d（t）為未建模動態和外界擾動。

定義擴張狀態x3=d（t），設d（t）的導數存在且有界，記ψ=d˙（t），則可增廣為：

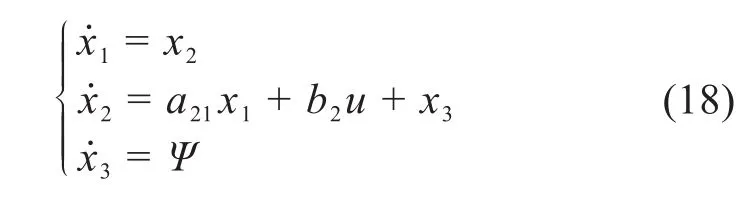
令zi（i=1，2，3）為系統中狀態變量xi的觀測值，定義觀測誤差e0i=zi-xi，故ESO設計為：

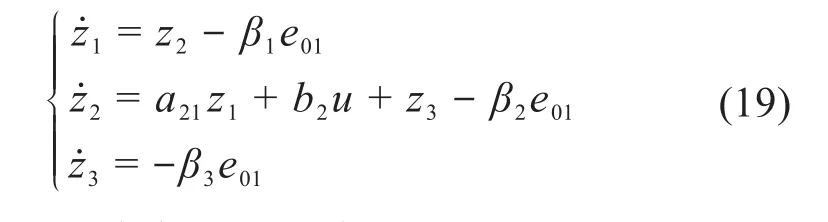
式中：β1、β2、β3均為觀測器增益。

通過調節β1、β2、β3使得系統趨于穩定。

3.2 ESO估計誤差分析

當系統穩定工作時，x3為一個常數，此時ψ=0，則觀測值與真實值之間的誤差為：

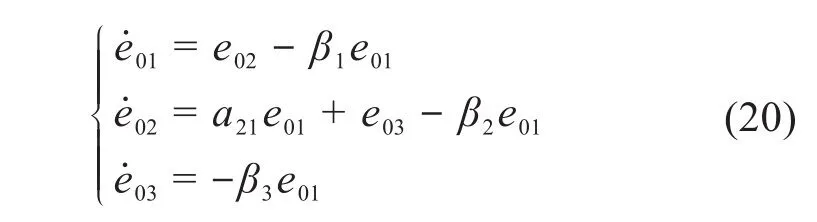
對式（20）進行拉氏變換，可得：

對式（21）進行整理，可得誤差模型的特征多項式為：

通過選擇合適的β=[β1β2β3]T，使得特征多項式滿足Hurwitz穩定。根據勞斯判據可得：

可以通過調節β1、β2、β3的值使得不等式組（23）成立。

3.3 改進的fal（·）函數

單純地采用狀態誤差對狀態和干擾進行估計，不能達到一種有效的跟蹤效果。使用fal（·）函數代替誤差，雖然可以有一個很好的效果，但是該函數在原點周圍連續不可導，故本文采用擬合的思路設計一種新的函數代替fal（·）函數，使得非線性函數在原點周圍具有良好的連續性、可導性和平滑性。

當|e|≤δ時，對非線性函數fal（·）進行改進，即在反雙曲正弦函數的基礎上構造擬合函數newfal(e，α，δ)，其表達式為：

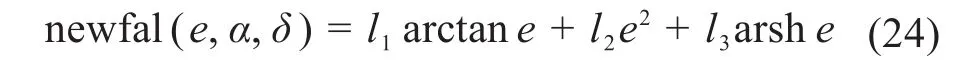
式中：e為狀態誤差；α為可調參數；δ為線性段區間長度。

根據擬合函數連續性和可導性的要求，所設計的參數l1，l2，l3須滿足：

將求得的參數l1、l2、l3代入newfal（·）函數，則有：

為了驗證所設計的newfal（·）函數的性能，對newfal（·）進行仿真。1）當δ=0.01時，分別取α=0，0.25，0.50，對newfal（·）函數進行仿真驗證；2）當α=0.25時，分別取δ=0.01，0.05，0.1，對newfal（·）函數進行仿真；3）取δ=0.01，α=0.25，分別對fan（·），fal（·），newfal（·）函數進行仿真對比。仿真結果如圖5所示。

由圖5（a）可知：α影響newfal（·）的幅值變化大小，α越大，斜率越大，輸出值變化越快；由圖5（b）可知：δ影響函數的非線性，其值越大，函數的非線性越強；由圖5（c）可知，newfal（·）函數在原點附近更加光滑，更符合ESO的要求。

圖5 函數性能仿真結果Fig.5 Function performanc simulation results

綜上所述，改進后的newfal（·）函數可以滿足設計要求。選擇δ=0.01，α=0.25進行控制仿真設計。

當觀測器收斂時，z3就是未建模動態和擾動的綜合估計值，可以對控制輸入進行補償以消除擾動。因此，設計如下的控制律：

式中：u為擾動補償后新型滑模控制器的輸出；z3/b0為ESO測得的總擾動實時補償，取b0=b2。

4 磁懸浮控制仿真研究

以電磁鐵的輸出電流i為輸入量、輸送帶的位置經傳感器檢測后獲得的輸出電壓u為輸出量建立磁懸浮控制系統并進行性能仿真。其中位置傳感器采用一維PSD（position sensitive detector，位置敏感檢測器），其增益為346.8 V/m。仿真中混合電磁鐵的結構參數如表1所示。

表1 混合電磁鐵結構參數Table 1 Structural parameters of hybrid electromagnet

利用Simulink/R2018a仿真軟件對混合磁懸浮控制系統進行仿真。在利用不同方法的控制仿真中，相同參數設為同一數值。設置ESO參數為：β1=1 000，β2=33 000，β3=3 320 000，滑模控制器參數為：k1=150，k2=20，k3=150，k4=80，?=2，β=0.5，λ=1，c1=900 000，c2=3 200，ke=60 000 000。SMC表示基于指數趨近律的滑模控制器，ISMC表示基于改進趨近律的滑模控制器，ESO-ISMC表示結合了改進ESO的ISMC控制器。

1）比較在3種控制策略下模型參考輸入時磁懸浮系統的響應性能。設定xr=33 mm，在3種控制策略下磁懸浮系統氣隙和速度的響應曲線分別如圖6、圖7所示。由圖6可知：在SMC控制下，氣隙與設定值有4 mm的偏差，說明磁懸浮系統不能很好地跟蹤軌跡；在ISMC控制下，雖然系統可以很好地跟蹤設定氣隙，但是出現了抖振現象；只有在ESOISMC控制下系統才能較好地跟蹤設定軌跡且無抖振出現。在圖7中，z2ESO-ISMC為觀測器估計的速度，可知其比在ESO-ISMC控制下輸出的速度更加連續。因此在無干擾狀態下，ESO-ISMC的控制效果較好。

圖6 模型參考輸入下磁懸浮系統氣隙響應曲線Fig.6 Air gap response curve of magnetic levitation system under model reference input

圖7 模型參考輸入下磁懸浮系統的速度響應曲線Fig.7 Speed response curve of magnetic levitation system under model reference input

2）比較在ESO-ISMC控制下恒定氣隙輸入和模型參考氣隙輸入時磁懸浮系統的響應性能。為了更好地對比2種不同輸入時系統的響應性能，對參考模型作出適當修改，使在2種給定輸入下系統具有相同的響應速度。2種不同輸入下磁懸浮系統氣隙和速度的響應曲線分別如圖8、圖9所示。從圖8可知：系統能在0.04 s后達到平衡，但在恒定氣隙輸入時系統的氣隙響應超調量為33.33%，而在模型參考氣隙輸入時氣隙響應超調量為18.18%，降低了15.15%。其次，由圖7、圖9可知，不同的參考模型可以使系統具有不同的響應速度，因此，可以通過調節參考模型使系統擁有不同的響應速度，以滿足系統不同的控制需要，這比恒定氣隙輸入更具優良性。

圖8 不同輸入下磁懸浮系統的氣隙響應曲線Fig.8 Air gap response curve of magnetic levitation system under different inputs

圖9 不同輸入下磁懸浮系統的速度響應曲線Fig.9 Speed response curve of magnetic levitation system under different inputs

3）比較3種控制器的抗干擾性能。分別用階躍信號和隨機信號模擬磁懸浮系統受到重載變化和物料碰撞的干擾。在階躍干擾和隨機干擾時磁懸浮系統的氣隙響應曲線分別如圖10、圖11所示。由圖10可知：在階躍干擾時，在SMC控制下系統需要更多的時間達到平衡點；在ISMC和ESO-ISMC控制下系統恢復時間更快，且系統具有相同的超調量，當達到平衡時在ISMC控制下系統仍有輕微的抖振出現。由圖11可知：在隨機干擾時，SMC的控制效果較差，在ISMC控制下系統抖振現象較嚴重，故ESO-ISMC具有較好的抗擾性能。

圖10 階躍擾動時磁懸浮系統的氣隙響應曲線Fig.10 Air gap response curve of magnetic levitation system under step disturbance

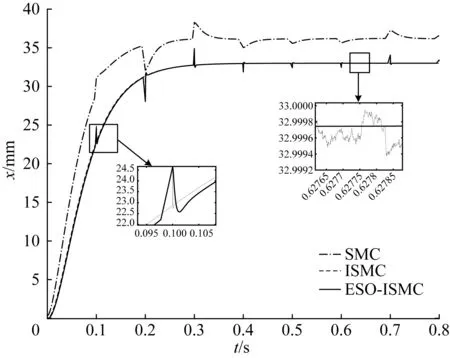
圖11 隨機擾動時磁懸浮系統的氣隙響應曲線Fig.11 Air gap response curve of magnetic levitation system under random disturbance

4）比較3種控制方法在模型失配情況下的控制效果。模型失配時磁懸浮系統的氣隙響應曲線分別如圖12、圖13所示。由圖12可知：分別在0.4，0.5和0.6 s時改變對象模型，在ISMC和ESO-ISMC控制下系統均有很好的控制效果，在ISMC控制下系統達到穩定更快，但是系統抖振現象比較嚴重。由圖13可知：在模型失配情況下，在0.4 s時出現氣隙異常突變時，在SMC控制下系統達到-7.2×1012mm后雖然后期能夠恢復到穩定平衡氣隙，但是突變氣隙值遠遠超過實際氣隙變化范圍，說明在模型失配情況下SMC控制失效。

圖12 模型失配時磁懸浮系統的氣隙響應曲線Fig.12 Air gap response curve of magnetic levitation system under model mismatch

圖13 SMC控制下模型失配時磁懸浮系統的氣隙響應曲線Fig.13 Air gap response curve of magnetic levitation system controlled by SMC under model mismatch

5）在ESO-ISMC控制下磁懸浮系統的電流如圖14所示。由圖可知，電流雖然偏離了設定值，但能夠很快達到穩定，輸送帶比只有電磁鐵進行控制時節能。

圖14 ESO-ISMC控制下磁懸浮系統的電流變化Fig.14 Current variation of magnetic levitation system controlled by ESO-ISMC

5 結 論

針對磁懸浮系統的開環不穩定性以及滑模控制中的抖振現象，提出了一種模型參考滑模控制與基于改進趨近律的滑模控制相結合的控制策略。設計了永磁-電磁混合結構、新的非線性函數newfal（·）和模型參考改進滑模控制方法。將所設計的控制策略分別與傳統磁懸浮滑模控制、基于改進趨近律的磁懸浮滑模控制進行仿真對比，結果表明：加入改進ESO可以有效減弱滑模控制帶來的抖振；在模型參考輸入的情況下，磁懸浮系統具有較小的超調量和較優的跟蹤性能；面對不同情況下的外界干擾，ISMC和ESOISMC使系統恢復時間更快，ESO-ISMC使系統具有極小的系統抖振。所設計的控制策略能極大提高磁懸浮系統的穩定性，對磁懸浮輸送機的輸送帶懸浮控制具有一定的參考價值。