看三視圖數正方體

吳麗娟

根據物體的三視圖確定這個幾何體的形狀是近幾年各地中考難點之一，許多同學遇到此類問題常感束手無策. 本文結合2021年各地中考相關試題，為同學們介紹其解題思路.

一、已知主視圖與俯視圖

思路：（1）將主視圖中從左到右每一列的小正方形數量填入俯視圖中從左到右每一列的小正方形中，得到的即為小正方體數量的最大值;（2）將俯視圖中每列最下面一個小正方形數字保留，其余方格中取數字“1”即為最小值.

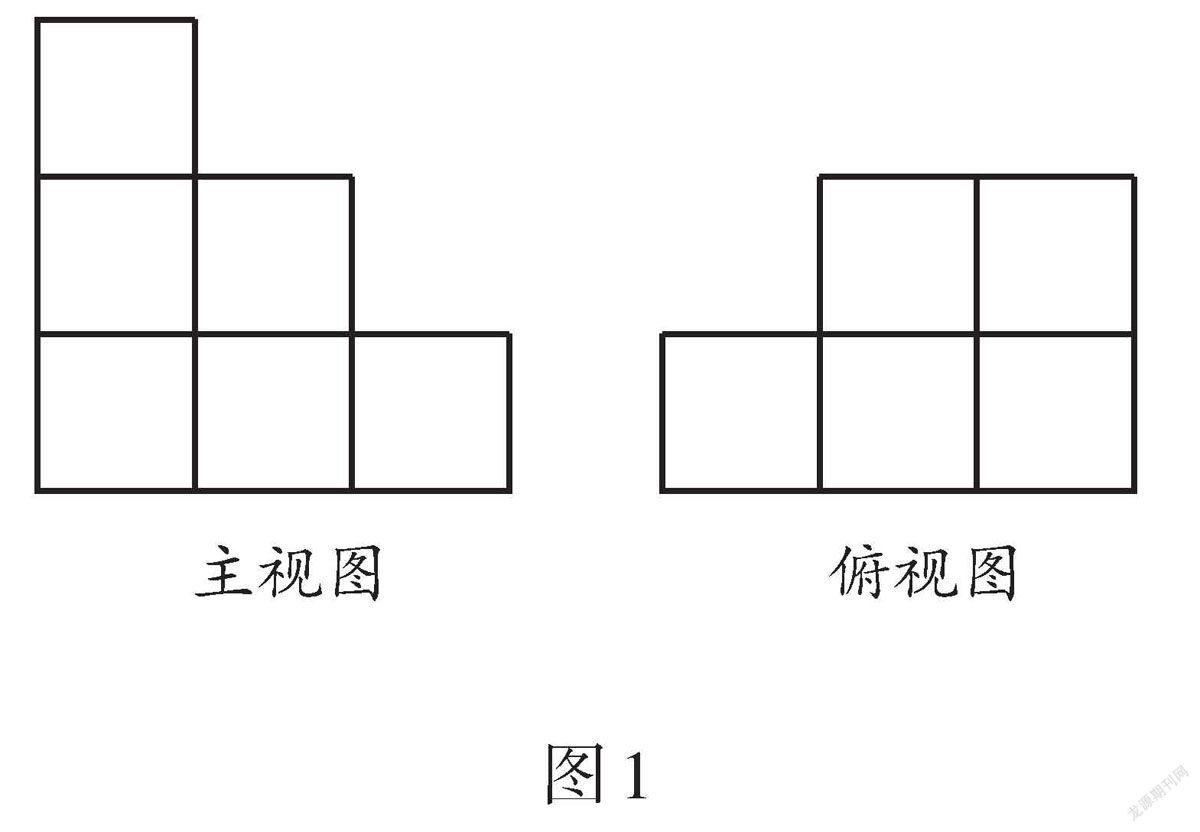
例1 （2021·浙江）桌上擺著一個由若干個相同小正方體組成的幾何體，其主視圖和俯視圖如圖1所示，則組成這個幾何體的小正方體最多有_________個，最少有_________個.

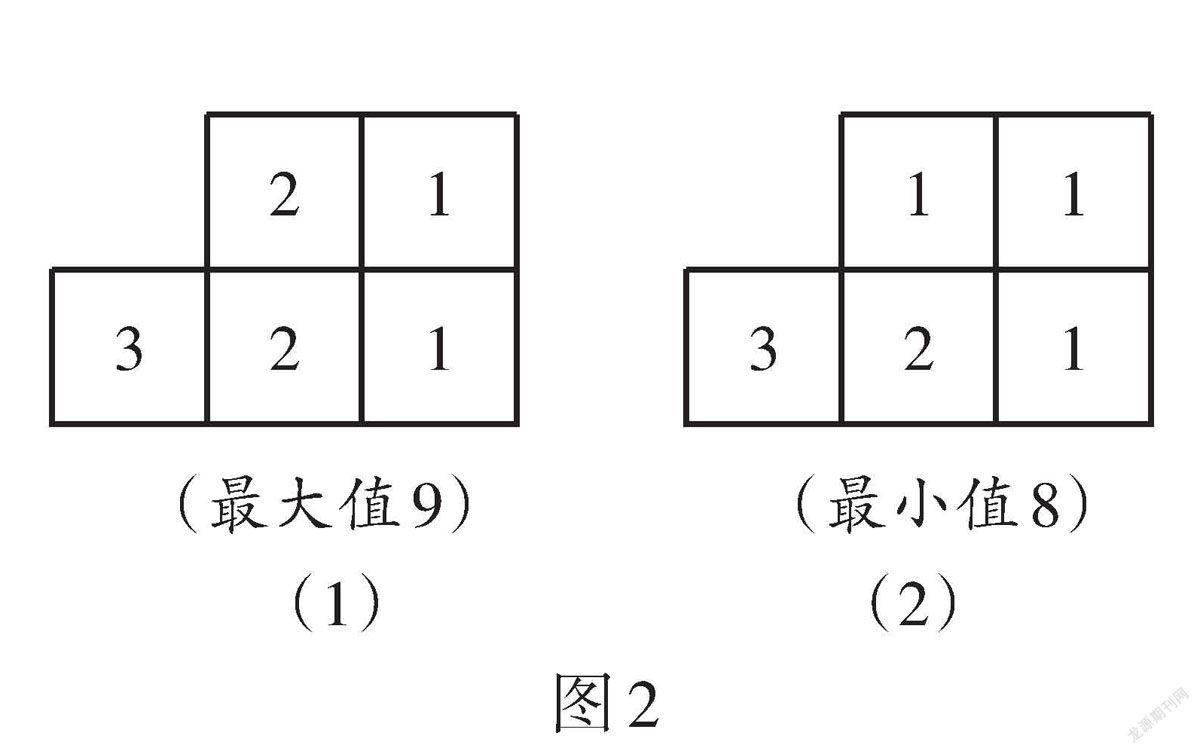
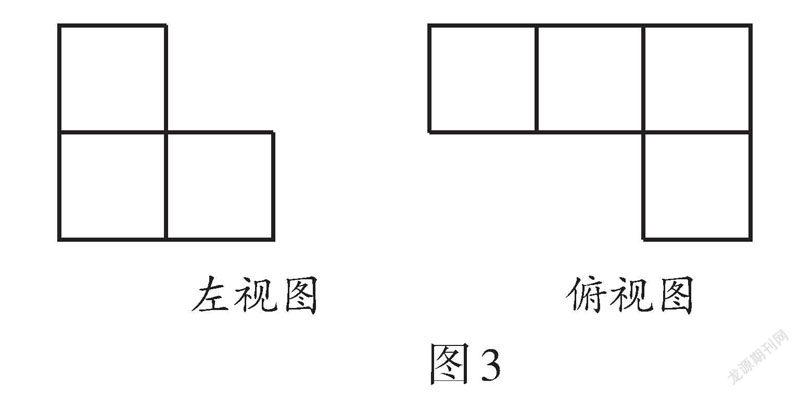
解析：如圖2（1），組成幾何體的小正方體數量的最大值為3 + 2 + 2 + 1 + 1 = 9;如圖2（2），每列最下面一個小正方形中的數量3，2，1固定不動，其余位置取最小值1，得到小正方體數量的最小值為3 + 2 + 1 + 1 + 1 = 8. 故填9，8，它的俯視圖和左視圖如圖3所示，則構成這個幾何體的小正方體的個數可能是_________.

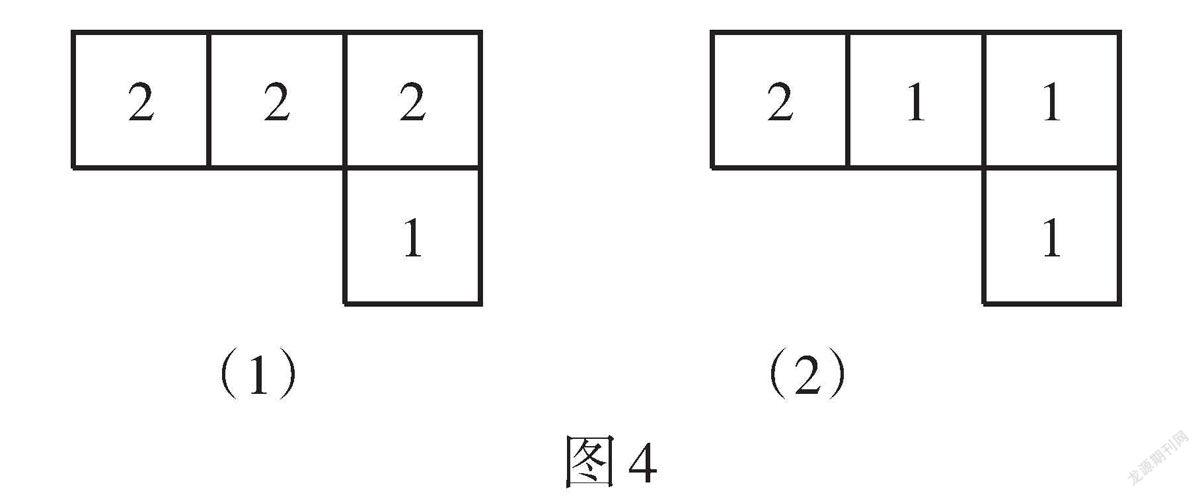
解析：如圖4（1），組成幾何體的小正方體數量的最大值為2 + 2 + 2 + 1 = 7;如圖4（2），每行最左面一個小正方形中的數量2，1固定不動，其余位置取最小值1，得到小正方體數量的最小值為2 + 1 + 1 + 1 = 5. 故填5或6或7.

點評：已知左視圖和俯視圖的問題與已知主視圖與俯視圖的問題相類似，區別在于將每行最左邊的空格位置固定，按方法操作即可.

三、已知主視圖和左視圖

思路：（1）以主視圖的列數為長、左視圖的列數為寬構建長方形，作為這個幾何體的俯視圖，當同一小方格中數字不同時取最小值，求出的即是組成幾何體的小正方體個數的最大值;（2）先確定長方形中數字相同的小方格內的數字，其他小方格中的數據固定為數字“0”，求出的即是組成幾何體的小正方體個數的最小值;（3）若長方形中某列或者某行的方格中沒有相同的數字，則結合主視圖和左視圖確定方格中的最大值.

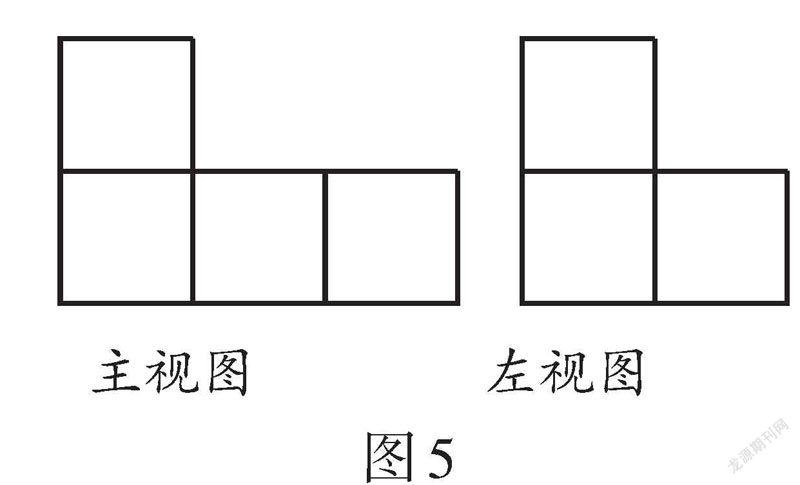
例3 （2021·江蘇·泰州）從正面和左面看由一些完全相同的小正方體搭成的幾何體，看到的形狀圖如圖5所示，則組成這個幾何體的小正方體的個數可能是 .

解析：主視圖的列數為3，左視圖的列數為2，構建3 × 2長方形，如圖6（1），如圖6（2），組成幾何體的小正方體數量的最大值為2 + 1 + 1 + 1 + 1 + 1 = 7;圖6（1），長方形中數字相同的方格數字為2，1，1，其余方格中數字固定為0，如圖6（3），得到組成幾何體的小正方體數量的最小值為2 + 1 + 1 = 4，空白方格中數據依次增加，得到組成幾何體的小正方體的數量可能是4或5或6或7. 故填4或5或6或7.

點評：已知主視圖和左視圖是最為復雜的一種情況，尤其是最小值的確定，需要重新分析主視圖和左視圖，確定空白列或空白行中某一小正方形中的具體數據.

（作者單位：大連匯文中學）

3683500338273