基于時頻脊線和階次分析的轉子故障診斷

庾天翼，李舜酩，龔思琪

（南京航空航天大學能源與動力學院，南京 210016）

0 引言

轉子在升速和降速過程中的轉速變化會導致非平穩信號的產生。對于非平穩信號，通過信號采樣獲取的振動信號不再具有周期性，故無法采用傳統的傅里葉變換進行信號處理和振動分析。傳統振動信號分析包括振動信號獲取、信號處理、信號特征提取、模式識別和智能決策，不適用于非平穩信號的故障診斷。因此，非平穩信號處理和分析方法成為了研究熱點，同時，也引起了國內外故障診斷研究領域眾多專家的關注。

變轉速動態信號處理及故障診斷方法的主要研究技術路線是以階次分析及其衍生方法為主。機械故障診斷領域著名學者澳大利亞新南威爾士大學Randall 和法國里昂大學Antoni指出：“階次跟蹤是解決變轉速問題最為直接和有效的方法。”階次分析實質上將非平穩的時域信號轉換成平穩的階次域信號，以此作為變轉速機械設備故障診斷的判斷依據。利用機械設備的轉速信息將等時間間隔采樣信號變換到等角度間隔的角度域信號，去除轉速波動對時域信號的影響，在階次域中觀察平穩信號的圖像，使得針對定轉速信號的處理方法重新發揮作用。

近年來，中國對階次分析的研究逐漸增加。王況等利用階次分析技術對行星齒輪箱進行分析，并且深入分析了行星齒輪箱局部故障的不同階次特征；馮珂利用計算階次圖譜和統計指標作為輔助手段，對Vold-Kalman 濾波器帶寬進行篩選優選，提出了一種Vold-Kalman 階次分析方法；楊武成提出了一種基于階次跟蹤和Hilbert 包絡解調的滾動軸承故障診斷的新方法，用Hilbert 包絡解調把低頻故障信號從高頻載波信號中解調出來，聯合階次跟蹤有效地提取了時變工況下非平穩振動信號的故障特征頻率并判斷故障類型；武英杰等提出一種基于變分模態分解（Variational Modal Decomposition，VMD）濾波和極值點包絡階次的特征提取方法，可以有效提取調幅信號中的調制階次，并且VMD 濾波使故障特征階次更加凸顯，易于故障識別。

由以上國內外現狀可知，階次分析法對采樣系統硬件依賴性極高。當下機械設備日益集成化，設備中某些重要部位并不適合轉速計的安裝，在缺少振動信號和轉速信號同步采樣設備的狀況下，階次分析難以實現。為此，本文結合2 維時頻分布的時頻脊線技術和階次分析方法，提出一種無需安裝轉速計即可實現階次分析的新方法，對轉子升降速信號進行故障診斷；并通過實測信號的對比試驗，驗證該方法的有效性。

1 非平穩轉子信號故障診斷理論

1.1 階次分析原理

階次分析法是將時域非平穩信號轉化為角度域平穩信號進行分析的方法。許多在時域、頻域乃至時頻域無法抑制、剔除的機械系統激振以及一些系統的隨機誤差，都可以在階次域中抑制。而一些故障信息會在階次域中得到較為清晰地顯現，因此采用階次分析法可提高故障診斷成功率。

階次分析的基礎就是轉速信號，階次表示為每周期事件發生的次數，是代表基于速度相關性振動的理想狀態。階次與轉速、頻率之間的關系為

式中：為階次；為頻率；為轉速。

階次分析的基礎是振動信號的同步采樣，同步采樣的質量則依賴于取樣系統的準確性和可靠性。階次分析方法有硬件階次跟蹤和計算階次跟蹤等。硬件階次跟蹤的采樣速率與轉速成正比，確保信號采樣頻率與轉速同步。計算階次跟蹤采用傳統采樣方法，異步采樣采集到振動信號和轉速信號，從異步采樣的轉速信號中，計算產生同步采樣數據所需的等角度重采樣時間。然后通過數據擬合或插值算法來對振動信號的這些時刻進行重采樣，獲得角度域信號，在對其進行快速傅里葉變換即可得到階次圖譜。

1.2 2維時頻分布的時頻脊線

對變轉速振動信號進行時頻分析后，一些與機械零部件動力學特性相關的曲線會清晰或隱約地出現，這些曲線在3 維時頻空間內的分布形態與“山脊”很像，如脊線標志或沿脊頂延伸的線。因此，在3 維時頻空間中把沿功率最高點延伸的線稱之為時頻脊線。時頻脊線往往表現為時頻面上的各種線條，包括直線、橢圓弧、拋物線、正弦曲線等，表征信號頻率變化的各種模式。

對于1 個時頻聚集性好且無交叉項的時頻分布，信號的能量總是沿著瞬時頻率集中分布，也就是說，時頻分布的能量脊線總是出現在信號的瞬時頻率附近。將3 維空間上的時頻脊線投影到2 維空間中，可以觀察到1 條函數曲線，這條函數曲線的每一點就近似乃至等于轉子在某一時間點上對應的瞬時頻率。因此可以將這條投影在2 維時頻面的曲線稱之為“時間—瞬時頻率”曲線。

振動信號在時域和頻域的能量可表示為

式中： ||()、 ||()分別為信號在時域和頻域的能量密度。

同理，信號在時頻域內的能量為

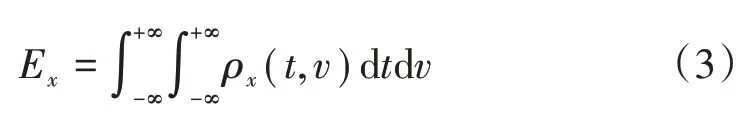
式中：ρ(,)為信號的時間頻率密度，是2次型的函數。

能量分布還滿足邊緣性質

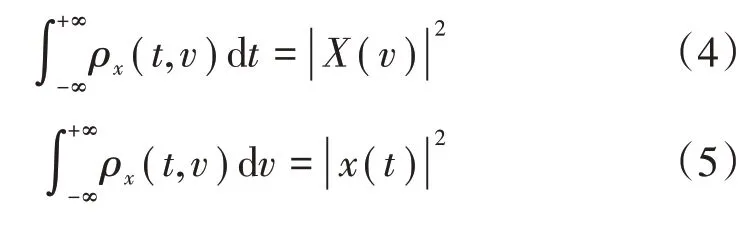
對于短時傅里葉變換來說，其時頻脊線是指時頻分布中每一時刻的峰值頻率

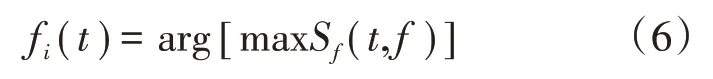
式中：（，）為信號的時頻分布。

時頻脊線總是集中分布在變轉速信號瞬時頻率分量周圍，故基于2 維時頻分布的脊線提取方法包含2 個步驟：（1）將振動信號映射到時頻域中；（2）采用峰值脊線提取法通過能量最高點提取信號的中心主頻率，從2維時頻面內識別出目標脊線。

2 非平穩轉子信號故障診斷方法

2.1 基于時頻脊線和階次分析的轉子故障診斷步驟

在缺少振動信號和轉速信號同步采樣設備的狀況下，階次分析難以實現。時頻脊線表征信號頻率變化的各種模式，頻率變化即為轉速變化，而且在映射過程和脊線提取過程中，信號的時間關系是同步的，因此時頻脊線可以作為振動信號的同步轉速信息使用。在僅僅采集到振動信號的情況下，采用基于2 維時頻分布的脊線提取法對振動信號進行脊線提取，將時頻脊線作為階次分析法所需的同步轉速信號，即可得到無需安裝轉速計的階次分析方法。

基于時頻脊線和階次分析的轉子故障診斷步驟如圖1所示。

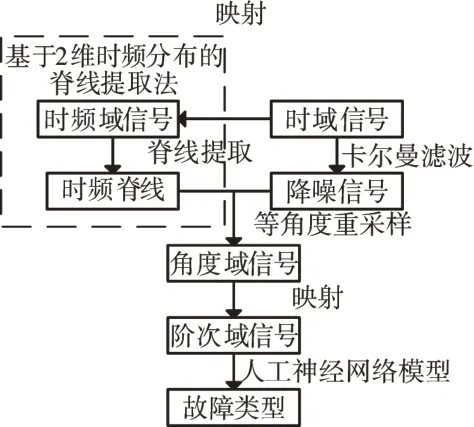
圖1 基于時頻脊線和階次分析的轉子故障診斷步驟

具體步驟如下：

（1）通過短時傅里葉變換（Short-Time Fourier Transform，STFT），將時域信號映射到時頻域中，采用峰值脊線提取法獲得時頻脊線

（2）進行卡爾曼濾波，對原始信號進行降噪預處理，結合提取出的時頻脊線中的轉速信息，對降噪信號進行等角度重采樣，獲得角度域信號

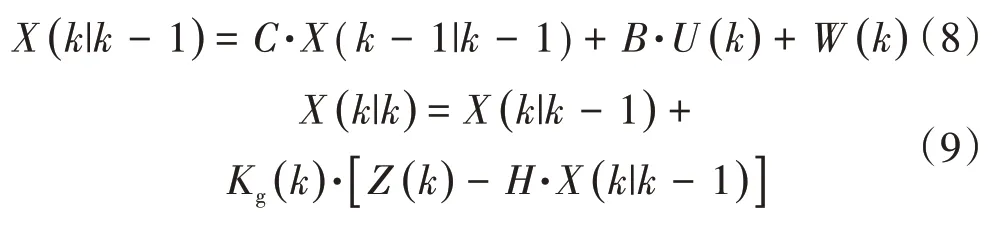
式中：（│-1）為利用前一狀態預測的結果；（-1│-1）為上一狀態最優的結果；（）為現在狀態的控制量；（）為過程的噪聲；為協方差；和為系統參數；（）為時刻的測量值；為測量系統的參數；為卡爾曼增益。

（3）將角度域信號映射至階次域中，獲得階次圖與階次域信號，此為故障敏感特征；

（4）將敏感特征輸入訓練好的人工神經網絡模型中，對轉子信號的故障類型進行分類。

2.2 轉子典型故障及其敏感特征

轉子的常見故障主要有轉子不平衡、轉子不對中和轉子碰摩等。轉子碰摩故障往往源于轉子不平衡和不對中故障，本文不做討論。

轉子不平衡是轉子故障中的常見故障之一。不平衡是質量和幾何中心不重合所導致的故障，轉子不平衡時偏心如圖2所示。

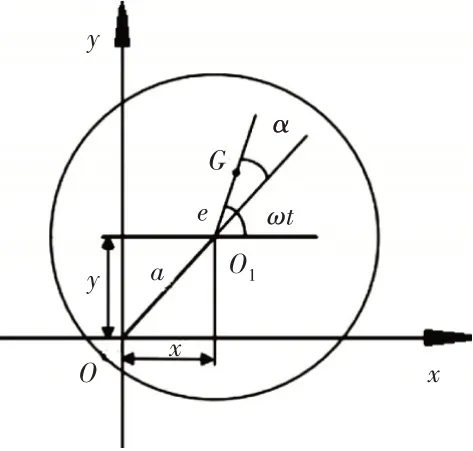
圖2 轉子不平衡時偏心

轉子不對中也是轉子故障中的常見故障之一。轉子不對中分為平行不對中、偏角不對中和平行偏角不對中3種，如圖3所示。

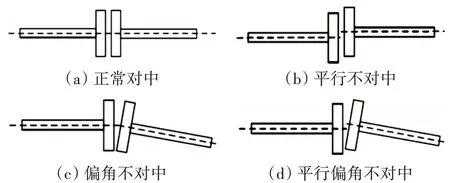
圖3 轉子不對中

階次域中轉子軸典型故障的敏感特征見表1。

表1 階次域中轉子軸典型故障的敏感特征

3 試驗驗證

3.1 試驗數據采集

本文采集轉子升速和降速過程中的振動信號作為試驗數據。試驗臺在0~5000 r/min 的轉速下工作，采用脂潤滑方式。電機參數的額定功率為0.75 kW，額定電壓為380 V，額定轉矩是5.0 kN·m。

試驗臺和傳感器安裝位置如圖4所示。軸上的2個盤是為產生轉速波動的扭轉振動信號而加裝的平衡盤。圖4（a）通過在大盤加裝質量塊產生不平衡故障，圖4（b）通過墊高右側支架產生不對中故障。采用2 個加速度傳感器同時測量軸輸入輸出端數據，傳感器型號及參數見表2。

圖4 轉子試驗臺

表2 傳感器型號及參數

試驗臺所采用的數據采集系統為LMS 系統，其采樣頻率為51200 Hz，帶寬為12800 Hz，分辨率為0.25 Hz。根據轉速和采樣頻率可知信號在1 個周期（即試驗臺旋轉1 周）所采得的數據點為3413 個。測試工況為緩加速，通過手動調節電機變頻器至最大轉速實現。

3.2 信號敏感特征對比

試驗臺測得2 組故障信號數據，從每組信號中選取4096 點進行分析。分別采用傳統敏感特征提取法與階次分析敏感特征提取法，提取并對比2 組信號的敏感特征，判斷階次分析法的效果。

3.2.1 傳統敏感特征提取法

傳統分析方法僅對信號進行降噪處理，再轉化到頻域中進行分析。轉子不平衡、不對中信號傳統敏感特征如圖5、6所示。

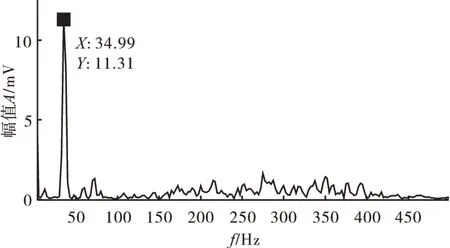
圖5 轉子不平衡信號傳統敏感特征

從圖5 中可見，計算轉速頻率約為35 Hz，圖中最大峰值出現在35 Hz 附近，是由于不平衡故障信號特征表現出的1X倍頻，是不平衡故障敏感特征。

從圖6 中可見，計算轉速頻率約為85 Hz，在84.98、160、272.4和339.9 Hz附近分別表現出1X、2X、3X 和4X 倍頻，根據轉子不對中故障信號敏感特征可判斷，該信號具有轉子不對中故障特征。

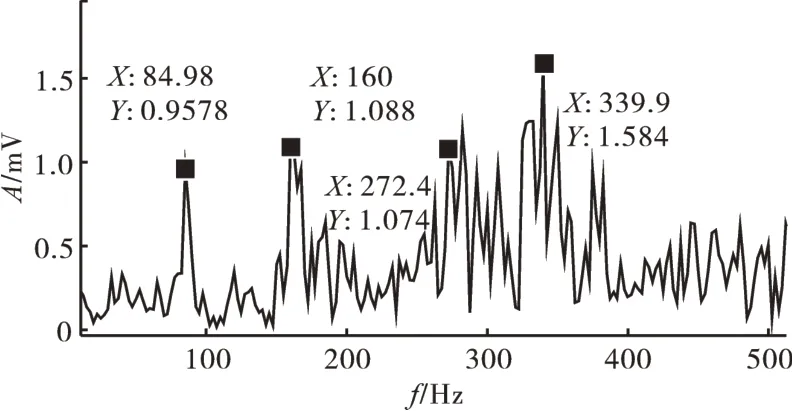
圖6 轉子不對中信號傳統敏感特征

3.2.2 階次分析敏感特征提取法

以轉子不平衡信號為例詳細說明階次分析法，并給出不平衡、不對中2組信號的階次域圖像。

3.2.2 .1 基于2維時頻分布的時頻脊線提取

對原始時域信號進行STFT，設置采樣頻率為12 kHz，海明窗函數長度取為256，為了提高計算精度，取2 窗函數之間的重疊采樣點為250。得到時頻譜如圖7所示。

從圖中可見在時頻面內信號的時頻特性，對比右側顏色等高線，觀察到試驗信號的高頻分量相對較少，可以將其忽略不計，而在低頻分量上，時頻圖中的能量分布較高，可知試驗裝置的敏感特征主要存在于低頻分量中，可重點關注圖中的低頻分量區。

在圖7中存在一些或清晰或隱約的曲線，尤其是在低頻分量范圍有一片明顯的明亮帶，說明在其附近一定存在峰值，如果將這些峰值連成線，即可得到所需時頻脊線。提取信號能量值最高點，之后再進行曲線擬合，如圖8所示。

圖7 時頻譜

試驗工況為緩加速，因此圖8 中紅色擬合曲線呈現上升態勢，頻率隨時間緩緩升高。對比試驗采集過程中轉速變換趨勢，這條2 維時頻脊線與其吻合度極高，可以作為振動信號轉速信息用于下一步的階次分析。

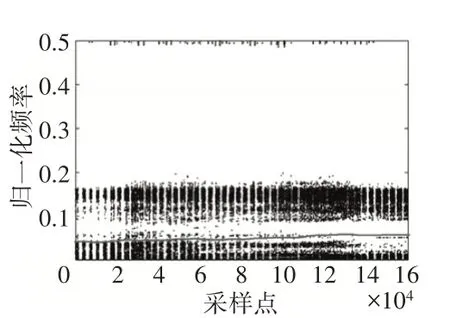
圖8 時頻脊線

3.2.2 .2 基于等角度重采樣的角度域變換

對轉子故障振動信號進行等角度采樣，即可得到角度域信號。從圖5 頻域中可知，雖然經過卡爾曼濾波后剔除大部分雜波，但是其中還存在很多雜亂的信號波紋，可能包含信號傳遞過程中由于機械結構激振出的信號分量和無法完全過濾掉的雜波，且轉速的波動變化也會產生非平穩信號，因此將信號由時域轉換到角度域中進行觀察，是機械故障診斷分析中重要一步。

以瞬時頻率為基礎的等角度重采樣，重構了濾波后的原始信號，將非平穩的時域信號轉變為角度域平穩信號，有效抑制了隨機噪聲和無關周期分量的干擾，可以更清晰地觀察到所需的敏感特征。結合提取出的時頻脊線，對濾波重構后的時域信號進行等角度重采樣，生成角度域特征信號，如圖9所示。

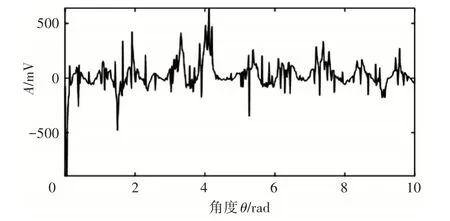
圖9 角度域特征信號

從圖中可見，圖像波形比時域波形相對集中，而且可以清楚地觀察到其主要集中幾段波形內，峰值也處于其中一處波形內。相對于主要波形，其他大多數范圍內的波形都相對較小，可以很明顯地區分出其只是一些不重要的分量，可以相對忽略不計。

3.2.2 .3 階次域信號分析

對生成的角度域信號進行STFT，得到角度1 階次域圖像，如圖10所示。

進一步將角-階域（圖10）的結果映射到階次譜上，得到轉子振動信號的階次譜，如圖11 所示。與原始信號圖像相比較，可見階次譜中出現了清晰典型的譜線峰值。

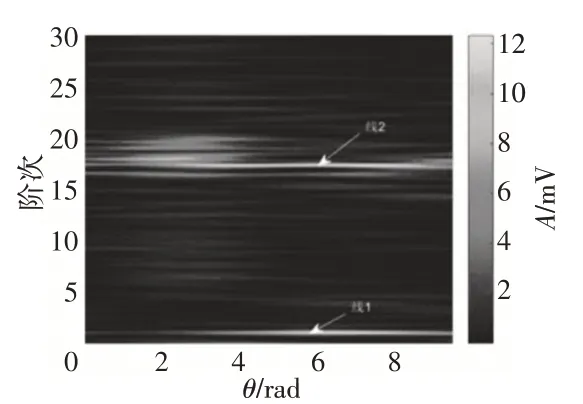
圖10 角-階域譜

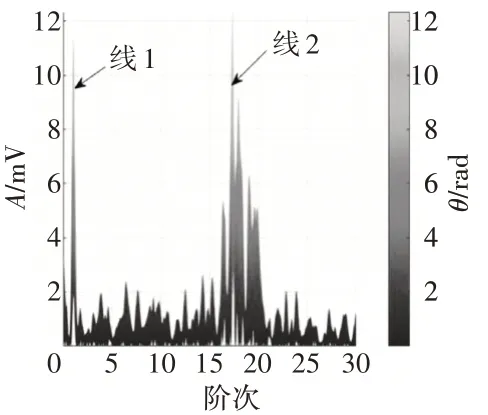
圖11 階次譜

將圖10、11 綜合對比分析，可見在圖10 中低階次區內存在1 條近似水平的直線，將其命名為線1；在高階次區同樣存在1 條近似水平的線，將其命名為線2。在將角1 階次譜投影到階次軸上后，線1、2 均為峰值譜線（圖11）。線1對應1階幅值，線2對應高階幅值，與前文介紹的階次域中典型的不平衡故障特征相符，可以判斷出發生了不平衡故障。

按照相同的步驟，轉子不對中信號的階次譜如圖12 所示。

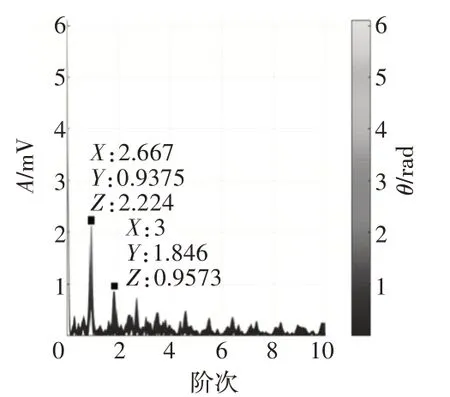
圖12 轉子不對中信號階次譜

從圖中可見，1、2 階幅值突出，與轉子不對中故障特征相吻合，說明發生了轉子不對中故障。

與傳統故障診斷法對比，階次分析法獲得的敏感特征更加清晰突出，噪聲與轉速波動產生的特殊頻率對診斷過程的影響較小，便于進行故障診斷分析。

3.3 基于BP-ANN的故障診斷

根據第3.1 和3.2 節的診斷步驟，使用BP 人工神經網絡（BP-Artificial Neural Network，BP-ANN）進行故障識別。通過對比試驗，驗證階次分析方法在故障診斷中的有效性。

轉子正常、不平衡故障、不對中故障數據集見表3。每個樣本的采樣點為4096，數據集共包含1200個樣本，隨機選擇其中600 個樣本作為訓練樣本集，其余600 個樣本作為測試樣本集，為了方便表示，將狀況類別標簽設置為1、2、3。

表3 數據集描述

設置BP-ANN 參數，中間結果周期為50，最大迭代次數為500，訓練目標誤差為0.001，學習率為0.001。為了消除隨機性的影響，每組試驗分別進行20次。

階次分析方法的20次診斷準確率結果如圖13所示。從圖中可見，數據集的訓練準確率均為100%，測試準確率超過99%，說明階次分析方法可以準確診斷出升降速過程中轉子的健康狀態。

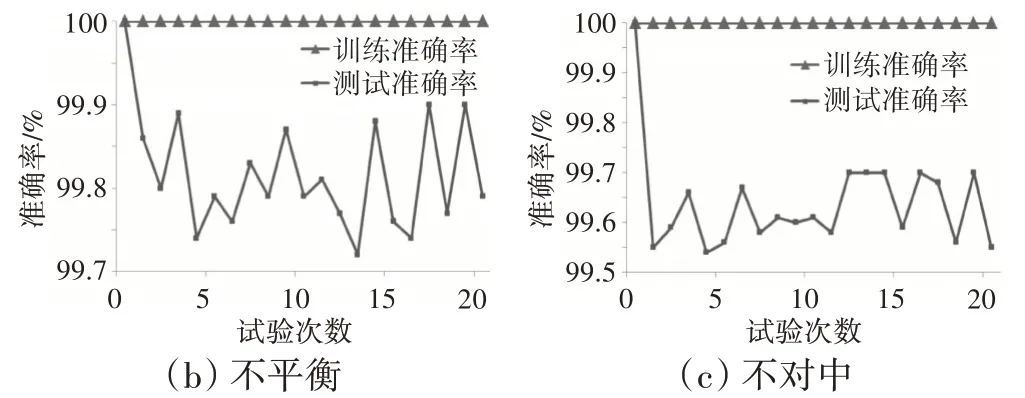
圖13 階次分析方法的20次診斷準確率結果

為了說明階次分析方法的有效性，采用傳統方法進行對比驗證，該方法同樣使用表3 的數據集。計算2 種方法的平均訓練準確率與平均測試準確率，見表4。從表中可見，階次分析方法的測試準確率穩定于99.62%~100%，標準差小于0.09%，均優于傳統方法。

表4 階次分析方法與傳統方法診斷結果對比

4 結論

（1）提出一種基于時頻脊線和階次分析的轉子故障診斷方法，并在人工診斷和機器診斷中獲得理想的應用效果；

（2）在3 維時頻空間中，信號能量沿著瞬時頻率集中分布，通過連接時頻分布中每一時刻的峰值頻率獲得2維時頻脊線；

（3）基于2維時頻分布的脊線提取法獲得的時頻脊線是振動信號的同步轉速信號，且與實際轉速對比吻合度高，可以作為同步轉速信息，用于階次分析。