試車數據驅動的渦軸發動機起動過程模型辨識

董 慶 ，李本威

（1.海軍裝備部駐蘇州地區軍事代表室，江蘇 蘇州 215011；2.海軍航空大學航空基礎學院，山東 煙臺 264001）

0 引言

航空發動機是高度非線性的時變系統，發動機模型在其性能及仿真、故障診斷、控制規律設計及實時監控等方面發揮著重要作用。針對渦軸發動機喘振試驗，建立準確的渦軸發動機模型可避免試驗中的某些風險和經濟損失。

目前，建立航空發動機模型的方法主要有解析法和系統辨識法。采用解析法建立發動機模型存在建模過程復雜且有一定的偏差和難以應用到發動機實時監控中等問題；而采用系統辨識的方法只需足夠的發動機輸入輸出數據就能簡單快速的建立較高精度的發動機模型。

傳統的辨識方法有最小二乘法、子空間狀態辨識法等。王磊等利用改進的子空間辨識法建立了某型渦扇發動機的小偏差狀態變量模型，但假設發動機是線性時不變系統，在一定程度上影響了模型性能。人工神經網絡（Artificial Neural Networks，ANN）、支持向量機（Support Vector Machine，SVM）和極限學習機（Extreme Learning Machine，ELM）等具有很好非線性學習能力的機器學習算法已越來越多地應用于航空發動機領域。丁凱峰等利用RBF 網絡建立了航空發動機辨識模型；陳超等利用人工神經網絡對航空發動機起動模型進行了辨識與仿真。但以上人工神經網絡都存在無反饋單元或者無延時單元等問題，而航空發動機是高度時變系統，傳統的神經網絡建立的發動機模型精度有時不能滿足實際的精度要求。Asgari 等利用非線性自回歸網絡（Nonlinear Auto Regressive with Exogenous Inputs Model，NARX）建立了某型單軸燃氣渦輪起動階段模型并進行了仿真分析，獲得不錯的效果。但NARX 網絡參數由隨機函數產生，在一定程度上影響了其性能。

螢火蟲算法（Firefly Algorithm，FA）是一種新型智能優化算法，具有參數少、尋優速度快等特點，但由于步長因子的影響會導致前期收斂速度慢、出現局部最優和出現峰值處不穩定震蕩等問題，為此提出變步長螢火蟲算法（Change of Step of Firefly Algorithm，CSFA），利用該算法對NARX 網絡參數進行全局尋優來改善網絡性能。

針對以上分析，結合已經獲取的渦軸發動機臺架試車數據，本文提出以試車數據為驅動、利用CSFA優化的NARX 網絡辨識渦軸發動機起動過程模型的方法。

1 CSFA-NARX網絡模型

1.1 NARX網絡

NARX 網絡為有外部輸入的非線性自回歸網絡。NARX 網絡不僅與當前時刻的輸入有關，也與過去的輸入輸出緊密相關，使用動態修正方法減少了模型修正的計算時間，樣本增加時矩陣階數不變，避免了矩陣求逆運算，提高了計算效率。

NARX 網絡通過引入延時單元及反饋來實現時間序列的動態預測，由帶有外部輸入的非線性差分方程表示為

式中：()為時刻的輸出值；()為時刻的輸入值；為自變量的非線性函數；為輸出延時階次；為輸入延時階次；(-)、(-)分別為輸出、輸入參數相應延時的數值。

NARX 網絡主要由回歸分析器和非線性估計器2部分組成，包括輸入層、隱含層和輸出層，如圖1 所示。回歸分析器（輸入層與隱含層）利用時刻及過去的輸入數據（），（-1），（-2），…，（-），和時刻過去的輸出數據（-1），（-2），…，（-），結合輸入權值和隱含層單元的偏置，由隱含層單元激活函數計算得到的值即為回歸分析器的輸出值，并傳遞給非線性估計器。回歸分析器的輸出值作為非線性估計器的輸入值，非線性估計器利用其非線性函數模塊和線性函數模塊估算輸入輸出之間的映射關系。

圖1 NARX網絡結構

某時刻第個隱含點的輸出h為

式中：為隱層節點使用的雙曲線正切sigmoid 函數；w()、w()分別為時刻第個隱層節點與輸入、輸出反饋之間的權值；b為第個隱層節點的偏置。

某時刻第個輸出層節點輸出()為

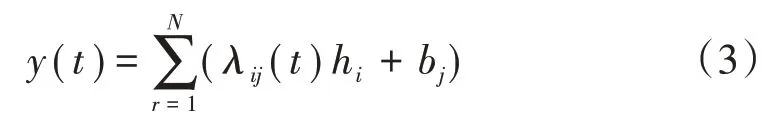
式中：λ()為時刻第個隱層節點到第個輸出層節點的權值；b為第個輸出層節點偏置；為隱含層節點數。

1.2 CSFA算法

FA 算法來源于大自然中螢火蟲的自然行為，群體中較亮的個體會吸引周圍的個體向這個方向移動來完成自身位置和亮度的更新，從而找出最優位置來實現尋優過程。FA 算法具有參數少、尋優速度快、效率高等特點，從而得到廣泛應用。但FA 算法迭代步長是固定的，導致若步長取較大值，則算法后期不利于求解局部最優，易出現峰值處不穩定震蕩問題；若步長取較小值，則算法前期不易快速找到全局最優鄰域且收斂速度較慢。故提出改進的變步長螢火蟲算法。

螢火蟲的熒光亮度和相互吸引度是螢火蟲算法2 個重要參數，發光越亮的螢火蟲位置越優，即目標函數值越優，最亮螢火蟲的位置即是最優解，發光越亮的螢火蟲對周圍的螢火蟲吸引度越強。

螢火蟲的相對熒光亮度和距離的平方成反比，相對熒光亮度為

式中：為螢火蟲最大亮度，即自身亮度（=0），目標函數值越優，自身亮度越大；為光強吸收系數，因熒光會隨著距離的增加和傳播媒介的吸收逐漸減弱，設置光強吸收系數以體現此特性，可設置為常數。

2只螢火蟲之間的距離r為

相對吸引度為

式中：為最大吸引度，即=0處的吸引度。

最優目標迭代，光亮較弱的個體會向光亮較強的個體移動，位置更新公式為

式中：x、x為螢火蟲和的空間位置；為步長因子；為[0 1]之間均勻分布的隨機因子；為可調整的正相關系數，即用kr代替固定步長。

CSFA算法尋優基本流程：

（1）初始CSFA 算法特征參數。設置螢火蟲數目、、、、和最大迭代步數或者精度要求。

（2）隨機賦予螢火蟲初始位置，計算螢火蟲的目標函數值作為自身熒光亮度。

（3）計算每對螢火蟲之間的相對亮度和吸引度，個體移動的方向由相對亮度決定。

（4）更新每個個體的位置，隨機移動處于最佳位置的螢火蟲，并重新計算個體的自身熒光亮度。

（5）判斷是否滿足終止條件，若滿足進行下一步，否則返回步驟（3）繼續。

（6）輸出全局極點值和最優個體值。

1.3 CSFA-NARX網絡模型

NARX 網絡初始參數初始化由隨機函數確定，大大影響模型的預測結果。因此，利用變步長螢火蟲優化算法全局搜索來確定NARX 網絡的輸入權值、輸出權值、隱層節點的偏置和輸出層節點偏置b。將獲得的、、和b返回NARX網絡用于模型的辨識。

CSFA-NARX網絡模型流程如圖2所示。

圖2 CSFA-NARX網絡模型流程

目標函數選取均方誤差作為模型的性能評價標準，來衡量模型預測值與實測數據的吻合程度

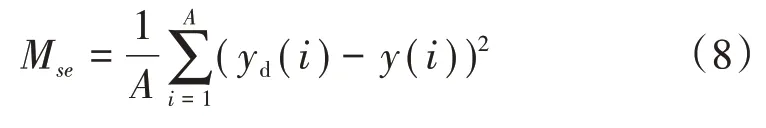
式中：（）為模型的預測值；（）為實測值；為樣本數量。

2 渦軸發動機起動過程模型建立

某型渦軸發動機的起動由起動機、發動機、點火系統、供油系統以及旋翼負載系統等多個系統協同工作來完成。其中，不同大氣條件、起動機特性、點火和供油特性及其旋翼負載特性是發動機模型的輸入量；在起動過程中的狀態和性能參數是發動機模型的輸出量。因此渦軸發動起動過程影響因素有：大氣溫度、大氣壓力、起動機的輸出功率、負載力矩、燃油流量。在渦軸發動機的起動過程中，通常負載力矩在常規大氣溫度大氣壓力下變化較小可忽略不計。同時，選取渦軸發動機參數燃氣發生器轉速、輸出軸轉速和渦輪后溫度作為模型的輸出參數來衡量發動機的起動性能。

發動機的狀態不僅與當前時刻發動機的各參數密切相關，還與此時刻之前發動機的狀態密不可分。因此，需要設置輸入輸出延時階次提高模型的精度，故構建的渦軸發動機起動過程數學模型表達式為

式中：、分別為模型的輸入、輸出量；為待辨識的渦軸發動機起動過程數學模型；、分別為輸入、輸出延時階次；根據發動機動態慣性，發動機模型輸入輸出參數延時階次通常設置為2。因此，將延時層的延時階次和均設置為2。

發動機轉子從靜止狀態逐漸加速到地面慢車狀態的過程稱為發動機的起動過程。根據起動系統和渦輪的功率變化情況，將起動過程劃分為3 個階段，建立發動機起動過程模型如圖3所示。

圖3 渦軸發動機起動過程不同階段

第1階段：按下起動按鈕1.25 s內，由起動機帶動燃氣渦輪工作，發動機轉速在規定時間內達到（0.08~0.12）×33400 r/min 時燃油系統開始工作點火。在此過程中發動機完全由起動機帶動工作，發動機的點火和燃油系統不工作，燃燒室無供油點火，渦輪后溫度約等于大氣環境溫度。

第2 階段：起動機和燃氣發生器共同工作帶動發動機加速工作，燃燒室開始供油點火燃燒。起動燃油調節器按起動燃油調節規律供油，直到燃氣發生器轉速達到（14000±1000）r/min時，起動機脫開。

第3 階段：起動機脫開后，燃氣發生器獨自帶動發動機加速工作至地面慢車狀態，起動過程完成。

整個起動過程需要限制在60 s 內。渦軸發動機起動過程模型輸入輸出參數見表1。

表1 發動機起動過程模型輸入輸出參數

3 CSFA-NARX網絡模型辨識結果及分析

結合NARX 網絡模型和建立的渦軸發動機起動過程模型，根據表1 將渦軸發動機模型的輸入輸出參數分別作為NARX 網絡模型的輸入輸出參數，結合已經獲取的試車數據，辨識得到渦軸發動機起動過程模型并進行驗證。

3.1 模型辨識數據的提取與預處理

本文采用的數據來自于某型渦軸發動機1000 h完整地面臺架試車試驗。該試驗的數據采集由測速發動機傳感器、不同類型動態壓力傳感器和不同類型溫度傳感器等配合數據采集系統完成，數據的采樣頻率為20 Hz，對發動機的進氣條件（如進氣溫度、進氣壓力和空氣流量等）、燃氣渦輪前后溫度、各轉速（燃氣發生器轉速和輸出軸轉速）、燃油消耗量和其他參數進行采集。

依據建立的渦軸發動機起動過程3 階段模型（表1），從提取的起動過程數據中選擇、、、、、和作為樣本參數。起動機的輸出功率由起動機的電流、電壓和效率計算得到。

本文所采用數據的4 組試車試驗起動過程各測試傳感器安裝位置相同且數據采集系統其它裝置均一致，進氣溫度設置為9.2、18.3、26.8、34.6 ℃，將4 組數據依次記為、、和。第1 階段每一溫度下選取25 個數據點，4 組共100 個數據點作為辨識樣本。第2、3 階段每一溫度下選取50 個數據點，4 組共200 個數據點分別作為辨識樣本，每組起動過程3 個階段共125個數據點。

對提取的辨識樣本進行剔除異常值、平滑、濾波和歸一化處理，在完成模型的訓練和驗證后對歸一化的數據進行反歸一化還原。

3.2 CSFA及NARX網絡參數設置

關于CSFA 算法初始參數的設置，參考文獻[22]，選取螢火蟲數目=85，最大迭代次數取200，最大吸引度=1，步長因子=0.12，吸收系數=1.02，正相關系數=2。

NARX 網絡輸入層節點數、輸出層節點數分別與發動機模型的輸入、輸出參數數目相同。通常，將隱含層數設定為1，隱含層神經元數由經驗公式確定

式中：為10~14的常數。

因此，本NARX網絡隱含層節點數=15。延時層的延時階次與發動機起動過程數學模型（式（9））保持一致，輸入輸出延時階次均設置為2。

3.3 模型辨識結果及分析

CSFA 算法和FA 算法在對NARX 網絡參數全局搜索尋優過程中，適應度值的變化過程如圖4 所示。從圖中可見，CSFA 算法在迭代前期具有較高的全局搜索能力，后期收斂也較快。

圖4 適應度值在尋優過程中變化

用辨識模型預測值與實測值最大相對誤差以及最大相對誤差均值來評價建立的辨識模型性能。相對誤差為

式中：（）為模型的預測值；（）為實測值。

結合預處理后的發動機起動過程數據，利用CS?FA-NARX 網絡模型對渦軸發動機起動過程模型進行回歸辨識。先將發動機起動過程3 階段模型分別辨識得出輸出參數值，因實際起動過程是連續過程，所以將3 階段辨識模型得到的輸出參數數據點連接起來，得到完整起動過程的不同輸出參數的輸出數據。

綜合考慮所使用的計算機性能和模型樣本數量，本文采用留一交叉驗證法（Leave-One-Out Cross Val?idation，LOOCV）對模型的性能進行驗證。例如，以、和為訓練樣本，以為驗證樣本得到辨識模型輸出參數、和的數值，與試車實測數據對比，結果和相對誤差分布如圖5~7 所示。4 組驗證樣本的驗證誤差見表2。

從圖5~7 和表2 中可見，輸出參數、和的辨識輸出結果都較好地逼近了實測數據，4 組驗證樣本中各出參數的最大相對誤差平均值分別為0.90%、1.51%和2.01%。表明本文提出的CSFA-NARX 網絡模型可用于渦軸發動機起動過程模型的辨識且模型精度滿足實際應用的精度要求，取得了良好的效果。

圖5 M4為驗證樣本ng辨識結果

圖6 M4為驗證樣本nr辨識結果

圖7 M4為驗證樣本T4辨識結果

表2 4組驗證樣本的誤差

3.4 不同算法比較

在MATLAB R2018a 平臺上，利用相同的訓練樣本和驗證樣本，通過對比CSFA-NARX、FA-NARX、NARX 和CSFA-BP 算法的辨識結果來驗證本文提出的CSFA-NARX算法的優越性。

CSFA-NARX、FA-NARX 和NARX 3 種算法延時層階次均設置為2，4 種算法隱含層神經元數根據式（10）設置為15，輸入輸出神經元數根據表1 設置，NARX 網絡均采用（Levenberg-Marquardt，LM）訓練算法，CSFA 和FA 算法螢火蟲數目85，最大迭代次數均取200，=1，=0.12，=1.02，CSFA算法中=2。

以、和為訓練樣本和為驗證樣本，不同算法得到辨識模型輸出參數n值與實測數據對比結果和相對誤差分布如圖8 所示；采用不同算法4 組驗證樣本的驗證誤差對比如圖9所示。

圖8 M1為驗證樣本不同算法ng的辨識結果

圖9 不同算法辨識結果誤差對比

從圖8、9 中可見，改進的變步長螢火蟲算法優化的NARX 網絡辨識模型精度高于螢火蟲算法優化的NARX 網絡辨識模型的，更優于直接采用NARX 網絡辨識模型的。而CSFA-NARX 網絡辨識模型精度與CSFA-BP 辨識模型的對比充分說明了具有反饋延時層的NARX網絡性能比傳統BP網絡更優。

4 結論

（1）辨識模型輸出參數、和與試車實測數據的偏差都在合理范圍之內，表明基于CSFA-NARX網絡模型對渦軸發動機起動過程模型辨識的方法具有可行性。

（2）采用留一交叉驗證方法對辨識模型的性能進行驗證，模型輸出參數、和的最大相對誤差均值分別為0.90%、1.51%和2.01%，表明基于CSFANARX 網絡模型對渦軸發動機起動過程辨識得到的模型精度滿足發動機實際要求。

（3）在相同的訓練樣本和驗證樣本情況下，基于CSFA-NARX 網絡模型對渦軸發動機起動過程辨識模型的精度優于FA-NARX、NARX 和CSFA-BP 算法辨識模型的，驗證了本文提出的CSFA-NARX 算法的優越性。

（4）本文建立的渦軸發動機起動過程辨識模型可用于對其他不同環境條件下（如高溫、高壓等）渦軸發動機起動過程性能的遞推估算，實現發動機性能參數預測，也可為渦軸發動機后續的試車試驗提供指導和為其起動過程性能優化奠定基礎。