寬厚比為5的超高層建筑風荷載特性研究

韓振， 李波,2， 甄偉， 楊慶山， 田玉基,2

(1.北京交通大學 土木建筑工程學院， 北京 100044；2.結構風工程與城市風環境北京市重點試驗室， 北京 100044；3.北京市建筑設計研究院有限公司， 北京 100045；4.重慶大學 土木工程學院， 重慶 400044)

超高層建筑是現代城市的重要組成部分，具有阻尼小，頻率低的特點，是典型風敏感結構。隨著人們對采光、通風等宜居性需求的增強，大寬厚比超高層建筑越來越多，例如：迪拜海灣沙灘大廈，杭州高德置地廣場等，寬厚比均超過了3。寬厚比是影響鈍體來流繞流特征及表面風壓分布的主要因素，早期研究者以二維矩形鈍體為對象，對寬厚比的影響展開了研究。Okajima[1]通過風洞試驗對寬厚比為1～4的二維矩形鈍體進行了研究，給出了不同寬厚比矩形鈍體Strouhal數隨Re數的變化。Norberg[2]通過風洞試驗，得到了不同寬厚比二維矩形鈍體的氣動力系數隨風向角的變化。Yu等[3-5]則重點分析了不同寬厚比二維矩形鈍體的來流繞流特征和風壓分布規律。鄭云飛[6]在不同寬厚比二維矩形截面兩端設置端板，研究了端板尺寸對各模型氣動特性的影響。王新榮等[7]還研究了均勻湍流場條件下，不同寬厚比二維矩形鈍體的風壓特征及其雷諾數效應。通過系列研究，已經掌握二維矩形鈍體的繞流及其風壓分布特征。但是，超高層建筑是三維鈍體[8]，并且還需要考慮大氣邊界層的影響。Lin[9]通過測壓風洞試驗研究了寬厚比為0.34～2.98的超高層建筑風荷載特性，對比了不同寬厚比超高層建筑層風力系數及基底力矩系數等，為結構抗風設計提供了參考。李永貴[10]以寬厚比為自變量，給出了矩形截面高層建筑根方差扭矩系數和基底扭矩功率譜的計算公式。Tamura[11]、顧明[12-13]在其不同形體超高層建筑風荷載特性系列研究中，包括了寬厚比為1和2的矩形超高層建筑。可以看出，具有較大寬厚比的超高層建筑與方形截面超高層建筑相比，側風面可能發生分離流再附，繞流機制將發生改變，風荷載特性將可能不同。但受以往工程實踐的限制，并未展開深入研究。

本文以一棟寬厚比D/B=5的工程實例為背景，通過測壓風洞試驗得到了大寬厚比超高層建筑風荷載，并將結果與東京工藝大學完成的寬厚比D/B=1的超高層建筑風洞試驗數據對比，說明了大寬厚比超高層建筑側風面再附現象，給出了風荷載特征，旨在為類似工程提供參考。

1 風洞試驗

1.1 試驗模型及風場

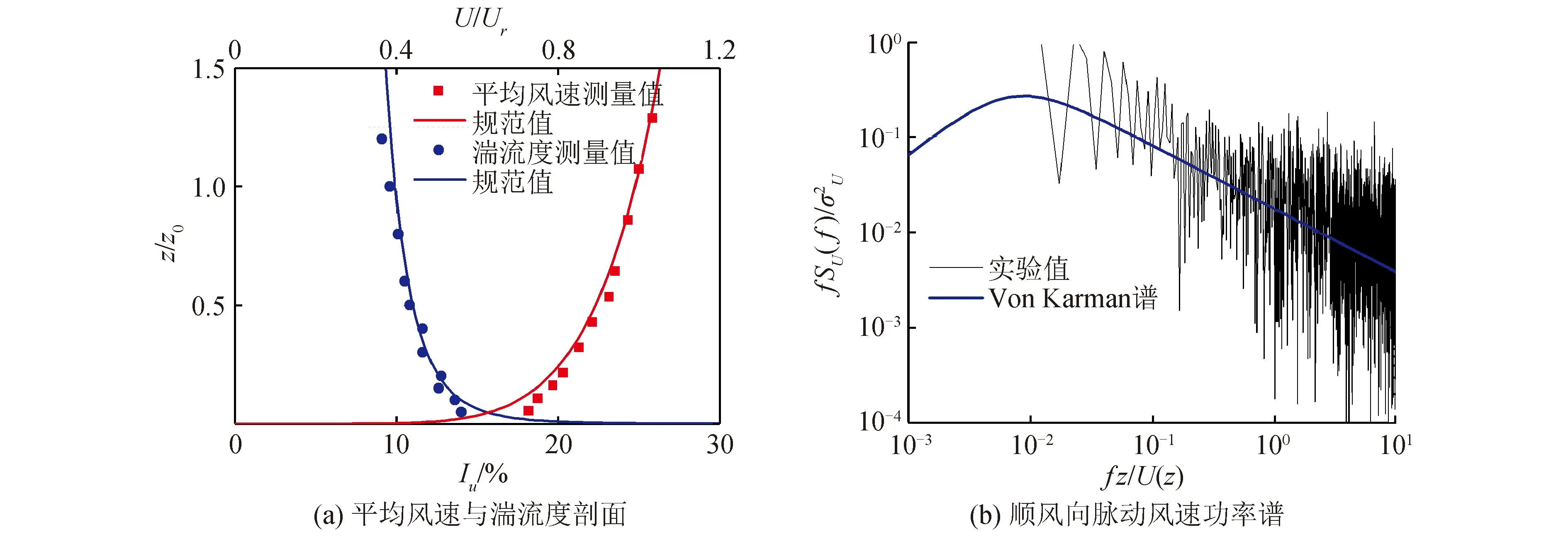
圖1 試驗風場Fig.1 Testing wind flow

風洞試驗模型如圖2所示，采用ABS材料制作，寬厚比D/B=5，幾何縮尺比為1∶200。建筑外立面布置了10層測點，每層35個，共計350個測點，建筑x向(沿建筑長邊方向)和y向(沿建筑短邊方向)對應的風向角分別為0°和270°，T為繞體軸的扭轉。風洞試驗中，通過電子壓力掃描閥測量模型表面風壓，采樣頻率為312.5 Hz，每個測點連續采集20 000個樣本。

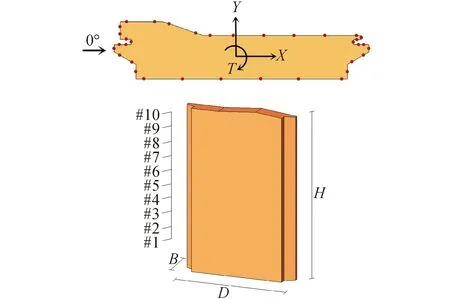
圖2 試驗模型及測點布置Fig.2 Testing model and taps distribution

選取東京工藝大學空氣動力學數據庫中寬厚比D/B=1的超高層建筑風洞試驗結果用于對比分析，該試驗與本次試驗風場均為郊區地貌類別，風剖面冪指數α=1/6。

1.2 數據分析方法

在分析建筑表面風壓時，通常采用無量綱壓力系數Cpn表示[14]：

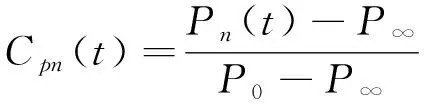
(1)

式中：Cpn(t)為測點n處t時刻的壓力系數，Pn(t)為掃描閥在測點n處t時刻測量的壓力值，P0和P∞分別是參考高度處的總壓和靜壓。

將模型某一測點層內所有測點表面的風壓系數按測點代表面積分別向垂直于建筑短邊x和長邊y兩個方向合成，可得到該測點層高度范圍內總的x向、y向及扭轉向風荷載，即層三分力，根據各層層三分力可求得基底力矩，然后再進行無量綱化處理即可得到層三分力系數和基底力矩系數：

(2)

(3)

(4)

2 試驗結果

2.1 風壓系數

圖3給出了寬厚比D/B=1，5的超高層建筑在0°風向角時，2/3高度處平均風壓系數分布圖。

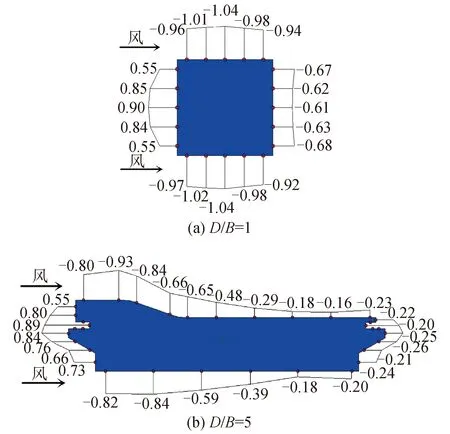
圖3 建筑物2/3高度處平均風壓系數分布Fig.3 Distribution of mean wind pressure coefficient at 2/3 height of buildings

可以看出，2種寬厚比建筑，迎風面平均風壓均為正值，其分布規律、大小相似；側風面受流動分離的影響，風壓均為負值，但大小受寬厚比的影響較大。D/B=1時，平均風壓沿側風面變化梯度很小，呈先增大后減小的趨勢，而D/B=5時，平壓風壓變化梯度增大，在側風面4/5處達到最小值后，又小幅上升；背風面受尾流的影響，風壓均為負值，且大小同樣受寬厚比影響較大，D/B=5時的背風面風壓僅為D/B=1時的1/3。結合二維矩形鈍體分析結果[5]，由以上現象可以推得，D/B=1時，側風面整體處于分離剪切層形成的分離泡中，且尾流較寬，側風面、背風面均產生較大的負壓。D/B=5時，分離流在側風面發生了再附，且在下游角點發生二次分離，使得側風面風壓梯度變化明顯，再附同時使尾流變窄，導致背風面風壓減小。

圖4給出了寬厚比D/B=1，5的超高層建筑在0°風向角時，2/3高度處脈動風壓系數分布圖。

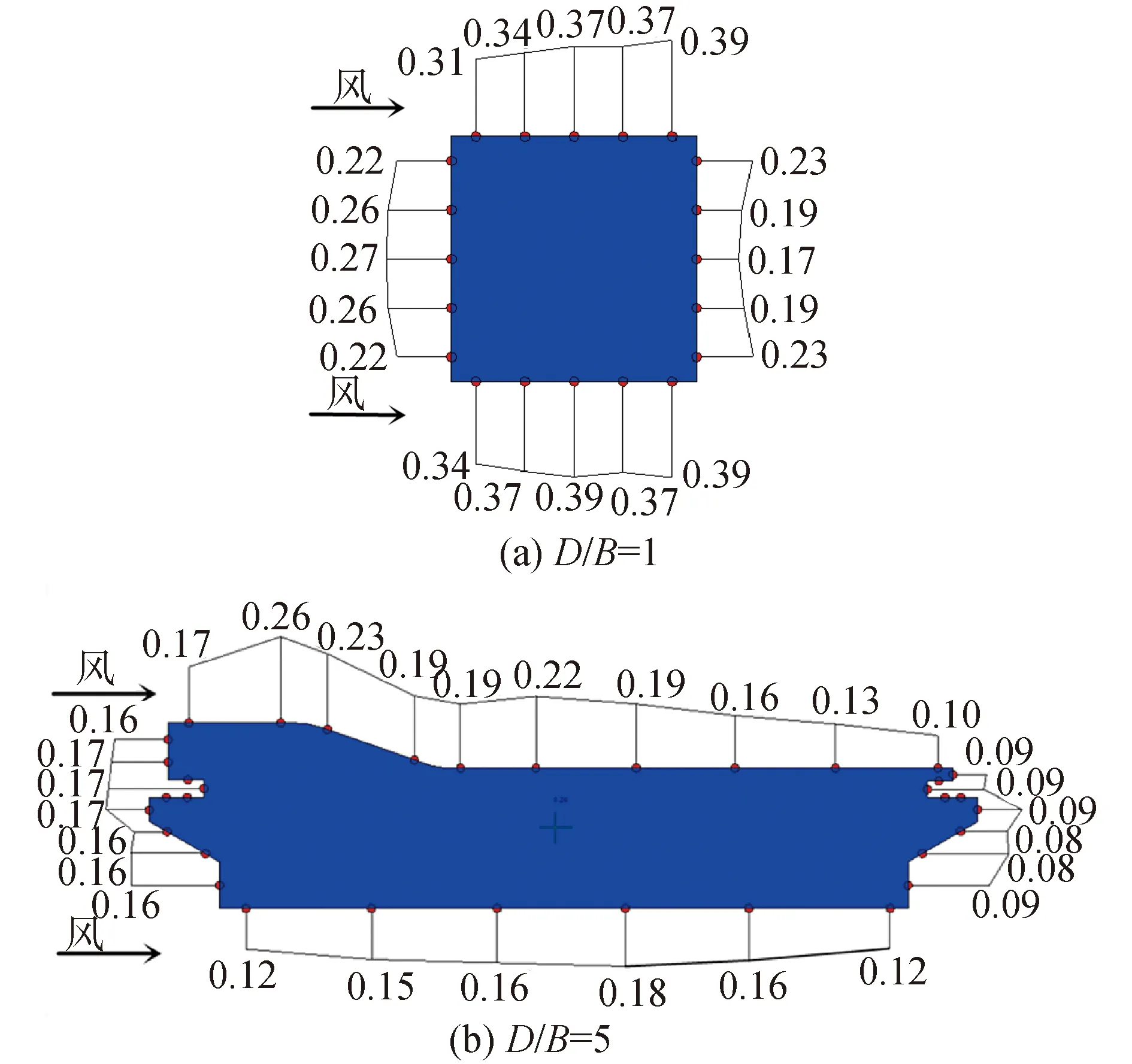
圖4 建筑物2/3高度處脈動風壓系數分布Fig.4 Distribution of fluctuating wind pressure coefficient at 2/3 height of buildings

可以看出，對于脈動風壓，當建筑寬厚比增大后，無論是迎風面，側風面還是背風面，風壓值均有所減小。值得注意的是D/B=1時，脈動風壓沿側風面逐漸增大，在尾部達到最大值；而D/B=5時，脈動風壓在側風面的分布總體呈先增大后減小的趨勢，變化較為復雜。文獻[15-17]認為側風面脈動風壓極值點的位置為再附點，用無量綱參數L/D表示側風面的相對位置，其中L為側風面某位置到迎風面前緣的距離。由圖4(b)可以看出，側風面Ⅰ (上)再附點出現在L/D=0.46處，側風面Ⅱ (下)出現在L/D=0.57處。需要說明的是，側風面Ⅰ (上)雖然在L/D=0.16處出現了脈動風壓最大值，但該處主要是受不規則形體的影響，并不是氣流再附點位置。

表1給出了寬厚比D/B=5的超高層建筑，不同高度處側風面再附點的位置。

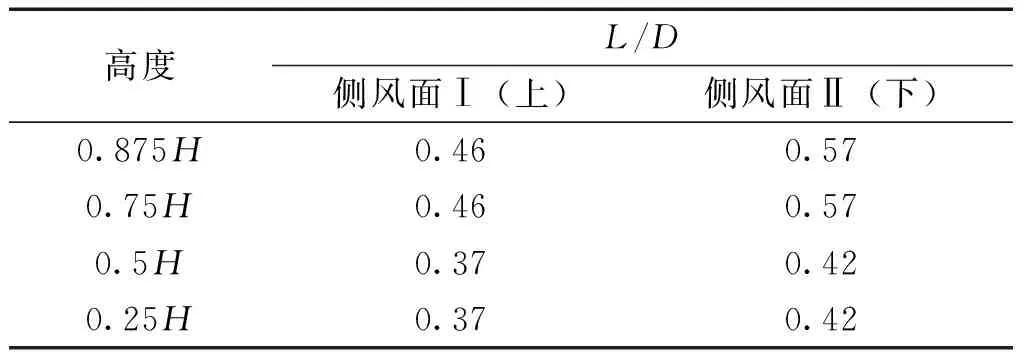
表1 側風面再附點位置(D/B=5)

可以看出，建筑不同高度處再附點的位置有所不同，建筑物上部側風面再附點的位置相比于中、下部位置靠后。該現象表明再附點位置與湍流度有關，建筑上部相比于中下部湍流度較小，分離流較強，因此再附點向后移動，與文獻[16-17]結論相吻合。

圖5給出了2種寬厚比建筑2/3高度處，側風面不同位置的測點與前緣測點的風壓相關系數。

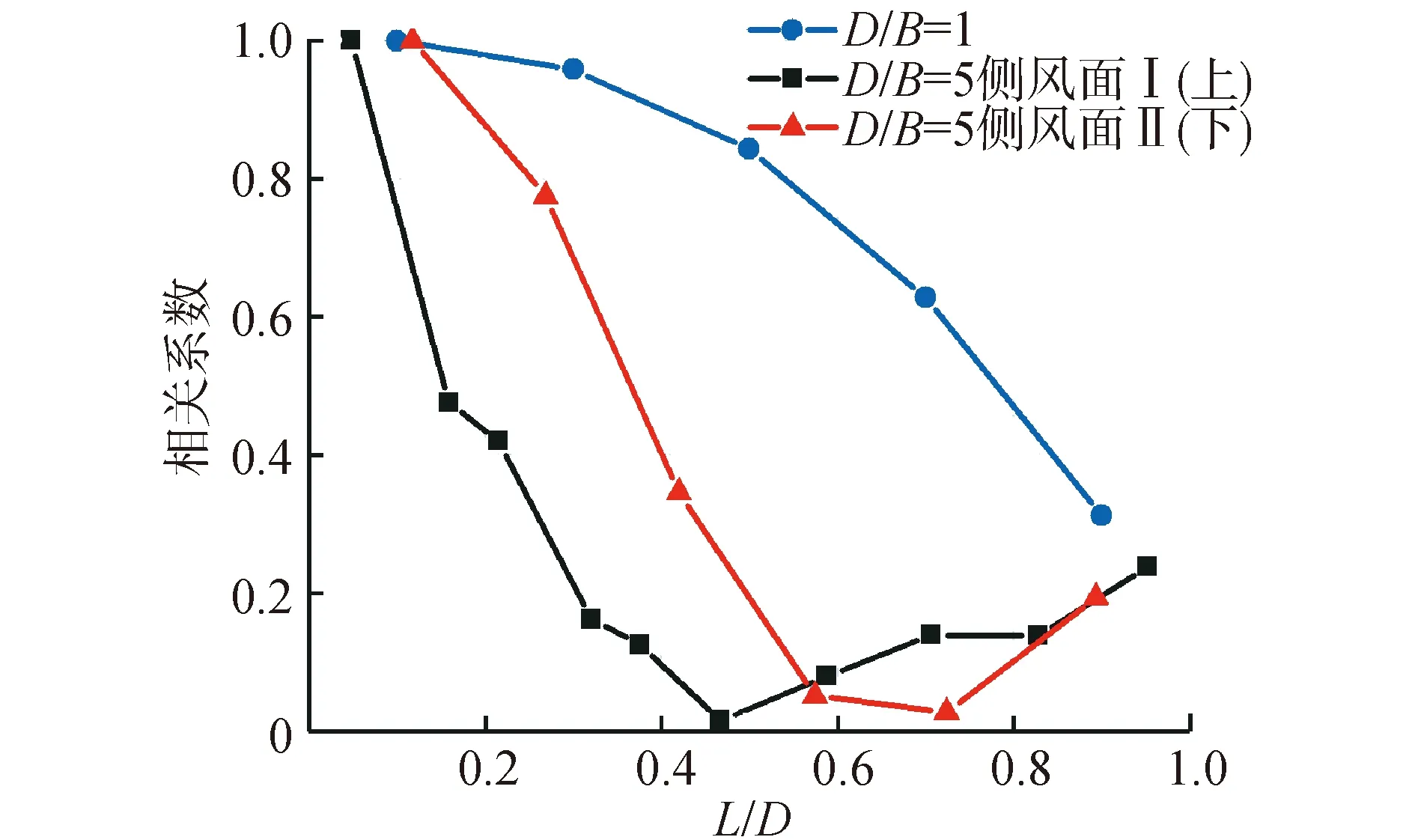
圖5 建筑2/3高度處側風面脈動風壓相關性Fig.5 Correlation of fluctuating wind pressure on the sideward surfaces at 2/3 height of buildings

可以看出，寬厚比D/B=1時，側風面風壓相關系數衰減速度較慢，各測點的相關程度較高。D/B=5時，側風面風壓相關系數衰減速度大幅加快，再附點附近相關系數接近于0，而后有小幅增大的趨勢。這也說明了D/B=1時，側風面整體處于分離剪切層形成的分離泡中，風壓作用機制相同，相關性強；D/B=5時，側風面發生了分離流再附，而后又在下游角點處發生二次分離，再附點附近風壓作用機制發生改變，導致側風面風壓相關性降低。

2.2 層風力系數

圖6給出了2種超高層建筑在0°風向角時，x向(Cx)、y向(Cy)和扭轉向(CT)層風力系數沿建筑高度的分布。

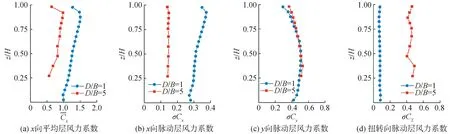
圖6 層風力系數沿建筑高度變化Fig.6 Variation of local wind force coefficients along the height of buildings

可以看出，2種寬厚比超高層建筑x向平均層風力系數隨建筑高度的增加總體上呈增大趨勢，最大值出現在高度0.9H左右，D/B=1、5對應的最大值分別為1.51和0.99，頂部由于受到三維繞流效應的影響，平均層風力系數減小。受分離流再附影響，D/B=5時尾流變窄，背風面平均風壓減小，導致x向平均層風力系數整體小于D/B=1；對于x向脈動層風力系數，其變化規律與平均層風力系數較為相似，D/B=5時x向脈動層風力系數同樣小于D/B=1；寬厚比對y向脈動層風力系數影響很小，均沿建筑高度的增加先增大后減小，且數值大小相近；扭轉向脈動層風力系數在D/B=1時較小，不同高度處基本保持在0.08左右，而D/B=5時，扭轉向層脈動風力系數整體較大，在建筑0.37H高度處出現最大值0.49。

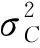
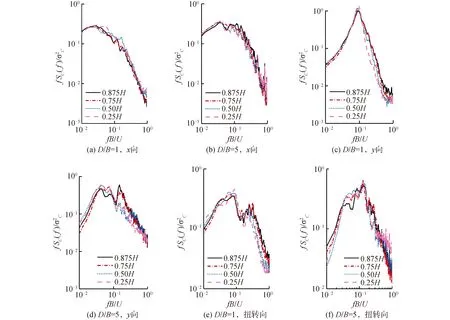
圖7 層風力系數功率譜Fig.7 Power spectrum of local wind force coefficients

可以看出，2種寬厚比超高層建筑，x向脈動層風力系數功率譜較為相似，總體呈寬帶過程，且不同層之間功率譜曲線變化基本一致；對于y向，D/B=1時，功率譜呈窄帶過程，在折減頻率0.09處出現一個與漩渦脫落有關的尖峰，能量較為集中。而D/B=5時，功率譜頻帶變寬，出現2個能量相當的譜峰，低頻譜峰對應的折減頻率范圍為0.04～0.08，高頻處的譜峰僅在建筑中上部出現對應折減頻率為0.15；對于扭轉向，D/B=1時，在折減頻率0.06～0.09及0.2～0.3處出現2個譜峰，而D/B=5時，僅在折算頻率0.13附近出現一個譜峰。

2.3 基底力矩系數

圖8給出了0°風向角時，2種寬厚比超高層建筑基底x向(CMx)、y向(CMy)及扭轉向(CMT)力矩系數間的相位軌跡圖，其中ρ為相關系數。

圖8 基底力矩系數間相位軌跡圖Fig.8 Phase-plane trace of base moment coefficients

可以看出，建筑基底x向-y向、x向-扭轉向力矩系數間相位軌跡呈橢圓形，且橢圓形長軸和短軸幾乎與坐標軸平行，D/B=1，5時的相關系數分別為0.008、0.015和0.045、0.075，相關性均較差；而y向-扭轉向間橢圓軌跡具有一定的斜率，D/B=1，5時的相關系數分別為0.555和0.418，相關性較強，但隨寬厚比的增大相關性減弱。

根據建筑基底力矩系數在0°風向角時的時程，表2給出了建筑基底某一主方向力矩系數達到極值時，從方向力矩系數的同步值。可以看出，盡管兩種超高層建筑基底x向-y向、x向-扭轉向間的相關系數很小，但當基底y向和扭轉向力矩系數分別取得極值時，x向同樣會取得較大值，具有極值相關性；同理基底y向和扭轉向間也存在較強的極值相關性，且隨寬厚比增大極值相關性增強。

表2 基底力矩系數極值與同步值Table 2 Maximum and synchronous value of base moment coefficients

圖9給出了0°風向角時，兩種寬厚比超高層建筑基底力矩系數間的相干函數曲線。

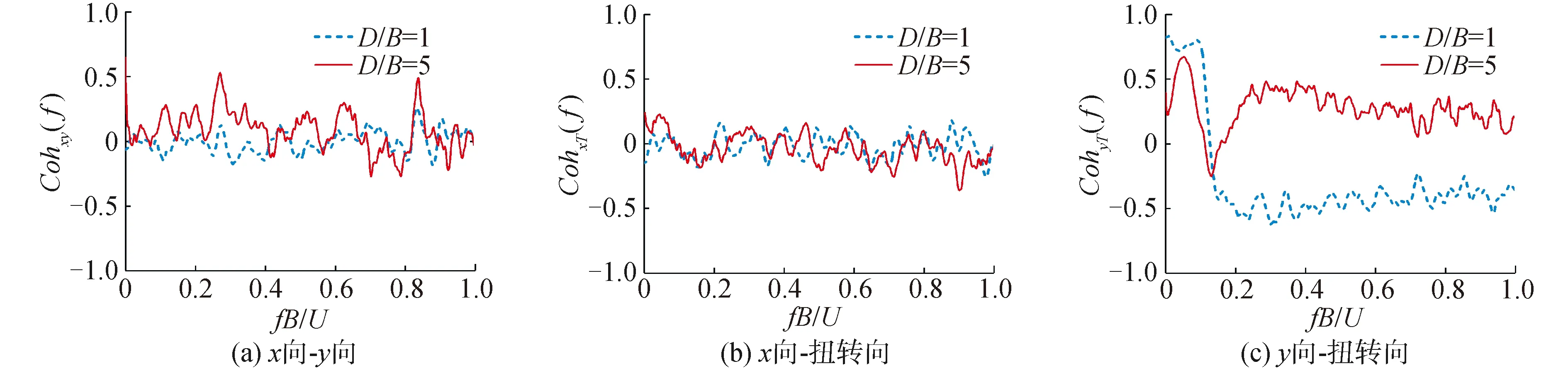
圖9 基底力矩系數相干性Fig.9 Coherence of base moment coefficients

可以看出，2種寬厚比超高層建筑基底x向-y向、x向-扭轉向力矩系數間的相干函數無明顯規律性，在0左右上下波動，相干性均較差；y向-扭轉向在0≤fB/U≤0.2范圍出現明顯峰值，D/B=1，5時對應的峰值大小分別為0.81和0.67、-0.25，相干性均較強，且峰值位置對應的折減頻率與y向脈動層風力系數功率譜峰值位置的折減頻率相近。當fB/U>0.2時，相干函數曲線逐漸穩定在某一值范圍內，其中D/B=1，5對應的穩定值分別約為-0.38和0.20。

3 結論

1) 寬厚比D/B=5的超高層建筑，側風面發生分離流再附，且在下游角點出現二次分離；側風面再附點位置與湍流度有關，湍流度越小，分離流越強，再附點位置越靠后。

2) 分離流再附使大寬厚比超高層建筑風壓作用機制發生改變，側風面風壓梯度變化明顯且相關性降低，再附點附近風壓相關系數接近于0，同時尾流寬度變窄，導致背風面風壓減小。

3) 與方形截面超高層建筑相比，大寬厚比超高層建筑扭轉向層風力系數較大，且y向和扭轉向層風力系數功率譜變化更加復雜，其基底y向-扭轉向力矩系數間也具有較強的相關性及相干性。因此對于大寬厚比超高層建筑的抗風設計，應重點關注其橫風向和扭轉向的風荷載效應。